はじめに
今回は線形近似について書こうと思います。
ところで制御屋の皆さんはコントローラーを設計する際に線形モデルを導出して利用することが多いでしょうか?
産業界において圧倒的なシェアを占めるPID制御の場合、だいたいはハンドチューニングやヒューリスティックな方法で調整することが多い気がします。
(私が昔所属していた開発現場でも大体はハンドチューニング+経験則でPIDとFFを設計していました)
線形モデルを利用して制御系設計を行うとなったら現代制御理論が代表的ですが、その際に利用する線形モデルはどの程度オリジナルの非線形なプラントで通用するのだろうかといったことを考えることがあると思います。
今回はそんな「いまさら聞けない線形近似ってなんだっけ」というのを自己の振り返りも兼ねつつ書いていこうと思います。
非線形システムと線形システムってなんだっけ?
ここで大ざっばなことを言うと世の中の大半の物理システムは非線形です。
たとえば、自動車の運動制御を考えたとき、走行速度によってステアリングの操作感って変わりますよね?
(一般道で低速で走っているときに曲がろうとすると割と大きいステア操作が必要だけど、高速で走っているときは少しのステア操作で良いとか)
制御で考えたときにこの非線形性って一般には厄介でして、できれば扱いやすい特性に近似したいと考えます。
そんな時に線形近似を利用します。
線形近似とは何かというと、元の非線形特性に対し、ある任意の一点における接線を引いた際の傾きと切片を求めて特性を近似する操作のことを言います。
イメージとしては次の図がわかりやすいと思います。
非線形システム$f(x)$に対して、赤丸の点$x_0$の点で接線を引いています。すなわち、接線は傾きと切片で示される一次関数ということになります。
そして、ご覧の通り、赤丸の点近傍では元の非線形システムの良い近似になっていますが、そこから段々と$x$方向に増減していくと全く異なる結果になります。
このように元の扱いにくい非線形なシステムを人が解析しやすい線形という領域に落とし込むことで制御対象の安定性を解析したり、コントローラーの設計をしていくのが線形制御理論のバックボーンとなります。
ちなみに、制御工学では非線形制御理論というものが存在し、この理論では線形近似の仮定なく、非線形特性のままに制御系を設計してしまおうというアプローチになります。(それはまた別の機会で)
テイラー展開
では実際に線形近似をしたいけど何をすれば良いの?ということになりますが、この時に使うのがテイラー展開と呼ばれる手法です。
テイラー展開は以下のような計算式で記述されます。
y \simeq f(x_0) + \left.\frac{\partial f}{\partial x}\right|_{x_0} (x-x_0) + \left.\frac{1}{2!}\frac{\partial^2 f}{\partial x^2}\right|_{x_0}(x-x_0)^2 + ...
上式で$x_0$は基準点であり、その周りで0次の項、1次の項、2次の項、、、、と計算し、その線形和をとることで元の非線形システムが表現されることを表しています。
ちなみに$\frac{\partial f}{\partial x}$はヤコビアン、$\frac{\partial^2 f}{\partial x^2}$はヘシアンと呼ばれます。
そして、線形近似では次のように2次以上の項をバッサリ切り捨てます。
y \simeq f(x_0) + \left.\frac{\partial f}{\partial x}\right|_{x_0}(x-x_0)
ここで、よく見てみると$(x-x_0)$を$x$と改めて置きなおしてみた場合、$\frac{\partial f}{\partial x}$が傾き、$f(x_0)$が切片となる一次関数の形になっています。
y = b + ax
これが線形近似の考え方です。
制御系設計における線形近似
線形近似について理解したところで本題である制御系設計における線形近似の活用を考えてみたいと思います。
ここで、非線形システムは次式で表されるものとします。
\dot{x}\ = f(x,u)
y = h(x,u)
$x$は状態、$u$は入力、$y$は出力であり、$f$及び$h$はそれぞれ非線形な関数となります。
これに対してテイラー展開を利用し、2次以上の項を無視すると次式となります。
\dot{x}\ \simeq f(x_0,u_0) + \left.\frac{\partial f}{\partial x}\right|_{x_0,u_0} (x-x_0) + \left.\frac{\partial f}{\partial u}\right|_{x_0,u_0} (u-u_0)
y \simeq h(x_0,u_0) + \left.\frac{\partial h}{\partial x}\right|_{x_0,u_0} (x-x_0) + \left.\frac{\partial h}{\partial u}\right|_{x_0,u_0} (u-u_0)
さらに$\Delta x = x - x_0$、$\Delta \dot{x} = \dot{x} - \dot{x}_0$、$\Delta u = u - u_0$、$\Delta y = y - y_0$と置き、$\dot{x}_0 = f(x_0,u_0)$、$y_0 = h(x_0,u_0)$であることを考えると、制御屋はご存じの線形な状態空間表現が得られます。
\Delta\dot{x}\ = A \Delta x + B \Delta u\\
\Delta y = C\Delta x + D \Delta u
ここで、各偏微分の係数は$A$、$B$、$C$、$D$と置きなおしています。
なお、上式では$\Delta$を意識して書いています。
教科書では$\Delta$を省略して書いていることが多いですが、あくまでも線形システムは基準点をベースとした偏位を表すモデルです。
それを確認するために簡単なテストをしてみたいと思います。
今回はSimulink Control Design™という制御系設計ツールで提供されているタンクシステムのデモを題材にします。
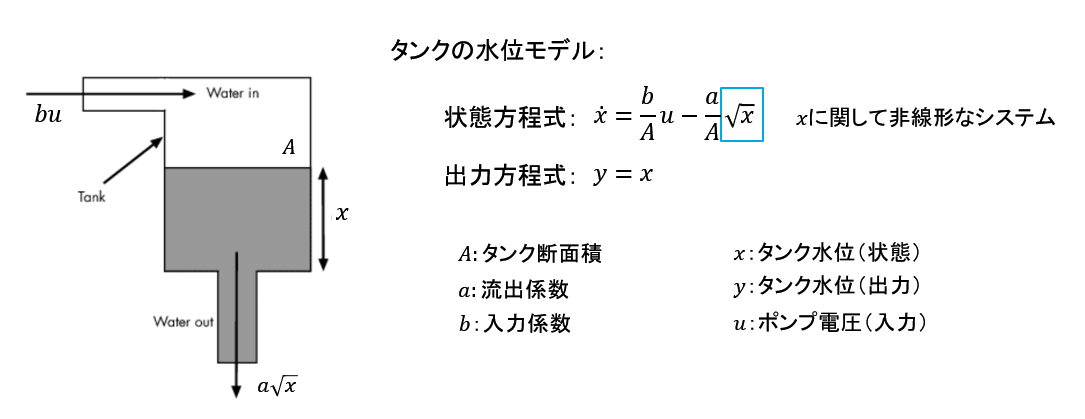
引用:https://jp.mathworks.com/help/slcontrol/ug/watertank-simulink-model.html
図に示すようにタンクシステムでは液面の水位を状態量$x$として見た場合、非線形なシステ
ムとなります。(水位に関する平方根が入ってくるため)
いま、水位は$x=10[m]$で平衡状態にあるとします。
Simulinkではモデルの指定した入出力点から平衡点を解析する機能がSimulink Control Design™から提供されています。
タンクシステムのモデルは下図で示す構成となりますが、入力であるポンプ電圧V及び出力の水位Hのライン上に何か矢印が置いてあるのがわかると思います。
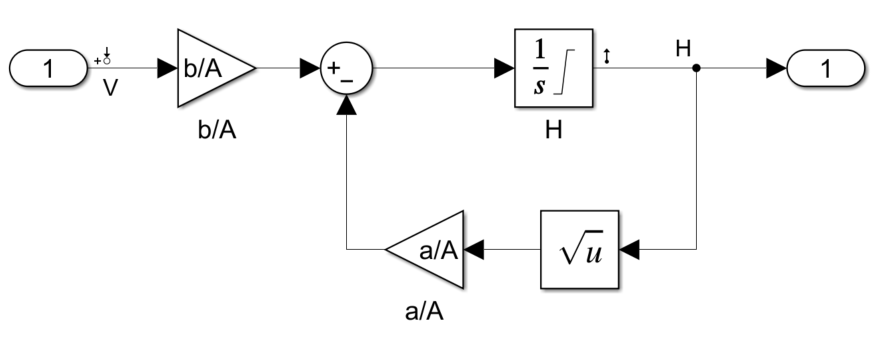
これは線形解析ポイントというもので、これらを解析したい入出力のライン上に指定することでその間の伝達パスを解析対象としてくれます。
あとはMATLABのスクリプトにてoperspec関数を利用してモデルから操作点情報の抽出を行い、既知の平衡点を指定する等行って、findop関数を実行すると指定した平衡状態における入出力値を算出してくれます。
open_system(mdl); % mdlはモデル名
% 操作点の抽出
opspec = operspec(mdl);
% 平衡点の指定
opspec.States.Known = true;
opspec.States.x = 10;
op = findop(mdl,opspec)
結果から、タンクの水位を10[m]で一定に保つためには入力であるポンプ電圧は1.2649[V]にしないといけないということになります。
あとはこの平衡点における線形な状態空間モデルをモデルから計算します。
スクリプトは以下に記載しています。
% 線形化
io = getlinio(mdl);
sys = linearize(mdl,io,op)
まずgetlinio関数を利用してモデルから線形解析ポイントの情報を吸い上げて、あとは平衡点の情報(op)と、モデル名(mdl)をlinearize関数に与えてあげると次のように結果を返してくれます。
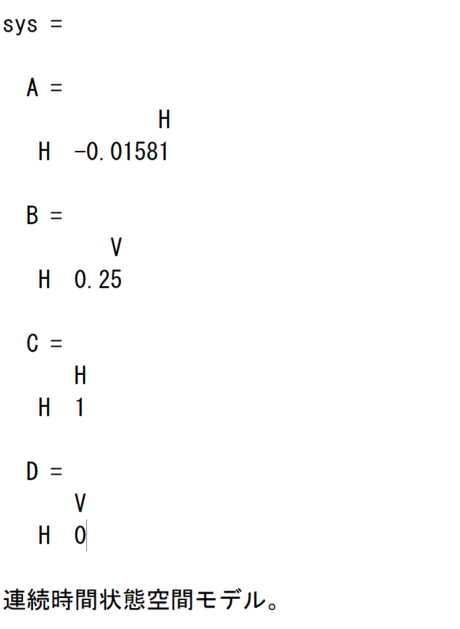
これが平衡点(水位10[m])における線形近似モデルということになります。
では得られたモデルと元の非線形モデルを比較して確認してみましょう。
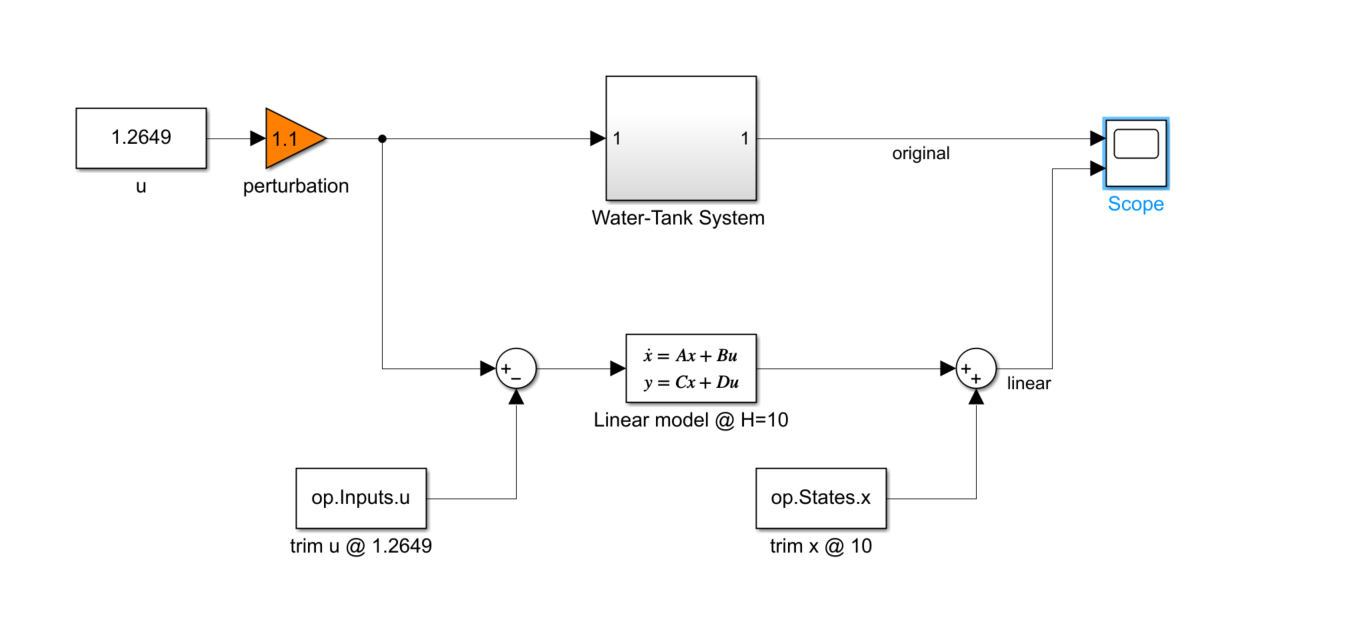
検証モデルの構成は次の図に示す感じです。
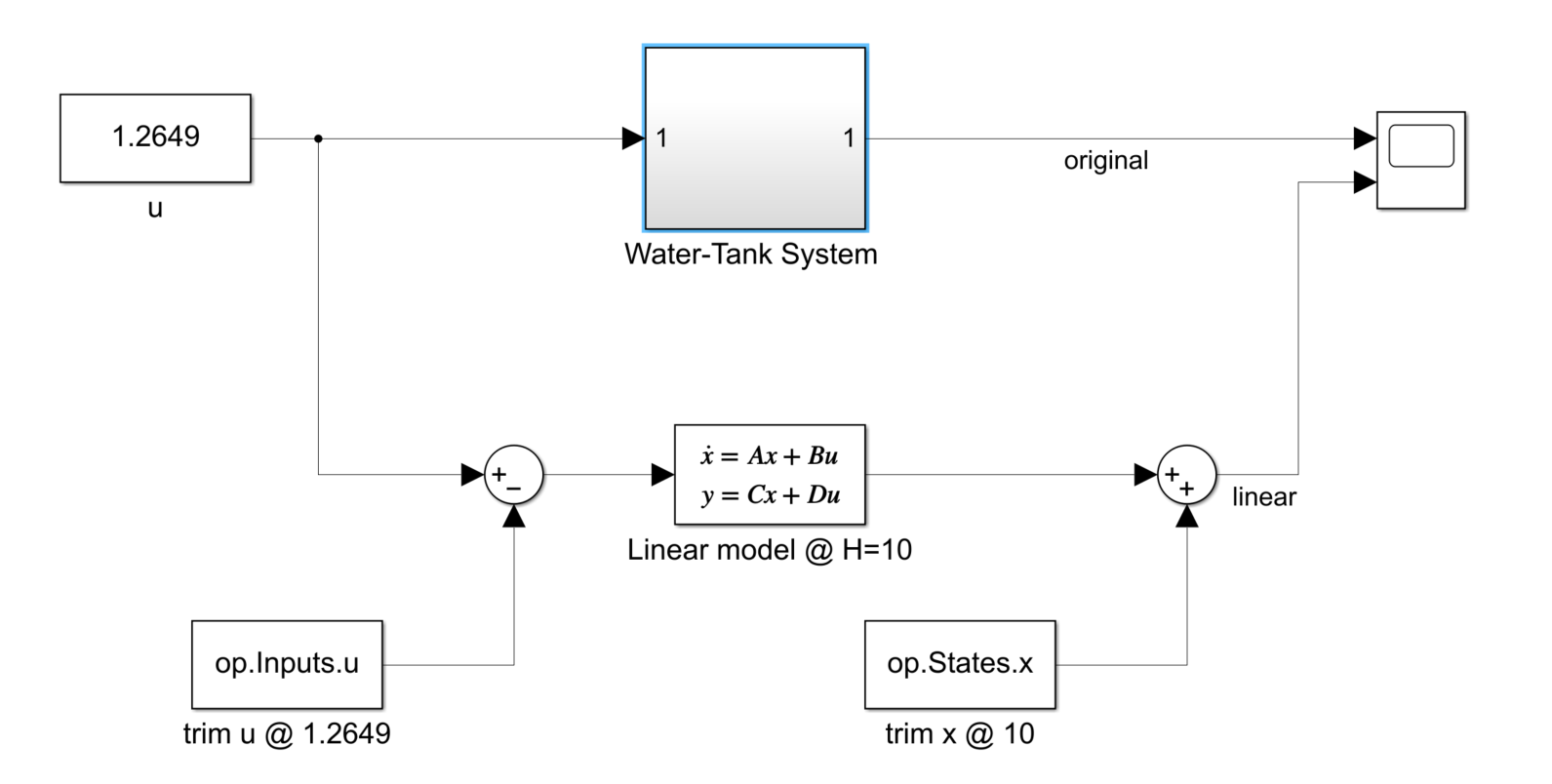
上段のサブシステムが元の非線形システム、下段のState Spaceブロックが線形近似したシステムを構成しています。
ここで注意点として、線形近似システムの方では平衡点(基準点)を考慮して、入力から$u_0$(1.2649)を差し引くのと、出力に$y_0$(10)を加算する処理が入っています。
ではシミュレーションを実行して、きちんとお互いの結果が10[m]でぴったりと一致するかを見てみます。
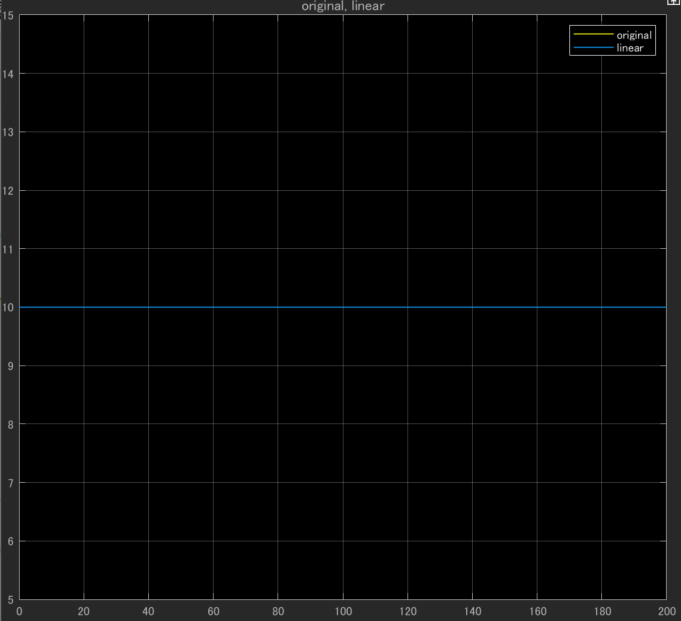
うまくいってますね。
ではちょっと入力を平衡点からずらしてみます。ここではわざと電圧に+10%ほど摂動を加えたいと思います。
入力が平衡状態からずれるので、水位は変動するはずです。その際にどういった応答を示すのか見てみます。
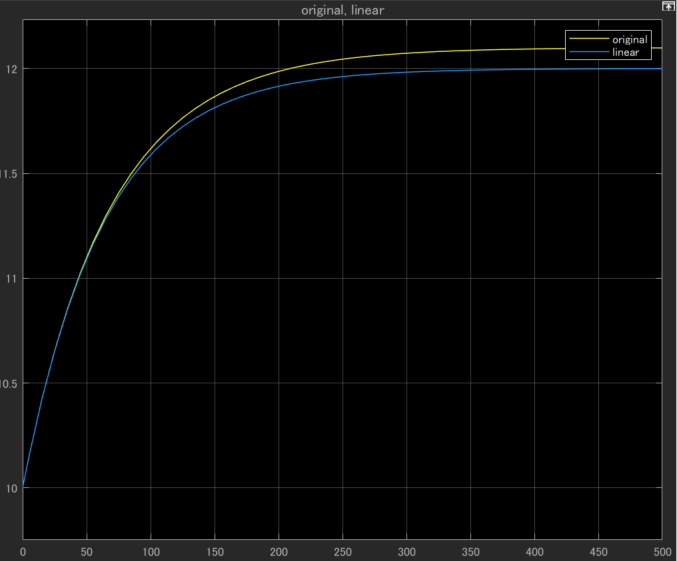
どうでしょうか。
今は入力を増やしている(ポンプの出力を上げている)ので、系への水の流入が増えています。
よって水位が上がるのですが、その増え方の様子が段々と離れていくのが見て取れると思います。
どうやら、水位10[m]の近傍である11[m]くらいまでは線形システムは良い近似結果になっていますが、そこからさらに離れていくと精度が悪化していきます。
そして定常状態では完全にオフセットしています。
さらに入力の摂動を増やしていくとその開きは大きくなっていきます。
(下図は+50%の摂動を加えた場合)
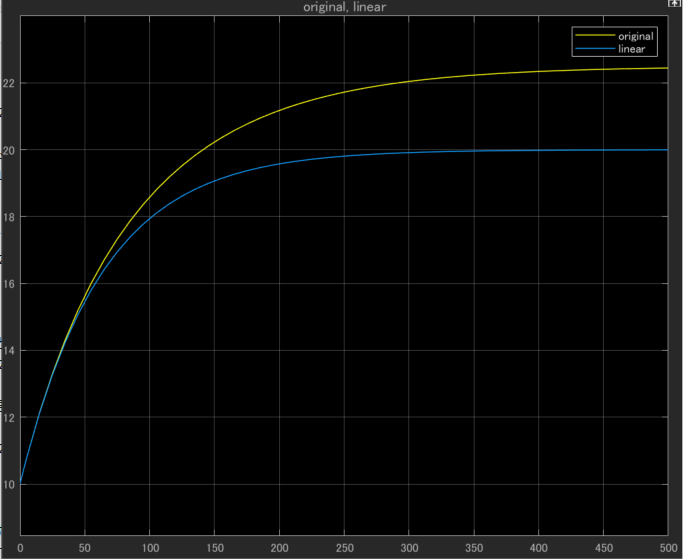
これが線形近似の精度の限界です。
タンクシステムは単純な例ですが、制御対象によって非線形性の強さは変わるので、線形近似が精度を保つレンジもまちまちです。
そのため、実用上では複数の動作点で線形近似を行って解析してみる必要があります。
特に制御系設計ではこうした非線形システムの特性を補償するために、複数の動作点でコントローラーや制御ゲインを設計し、切り替えて制御します。
これがゲインスケジューリング制御といわれるものです。
最後に
今回は大学の講義で習ったことのある線形近似について今更ながら振り返ってみました。
線形近似は人が非線形を理解するための大事なツールということを改めて考えさせられ、線形制御理論の偉大さを個人的に再認識しました(笑)
いまはROMやサロゲートモデルなどのBuzzワードが流行って、いわゆるAIで制御モデルを作ってしまおうという傾向にありますが、こうした解析的な視点で設計するアプローチも忘れてはならないかなと思う今日この頃です。(データドリブンモデルはすごい便利ですけどね。)

