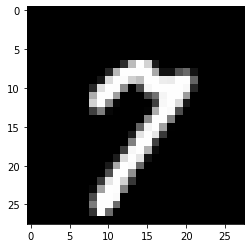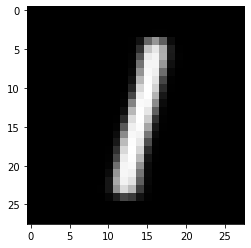Go to Qiita Advent Calendar 2024 Top
LoginSignup
27
20

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 1 year has passed since last update.

@gensal

【Pytorch】VAE（変分オートエンコーダ）を実装する

Posted at

はじめに

本記事に記載のコードは以下のnotebookに記載されています。
外部データなど不要ですので、とりあえずVAEを動かしてみたいという方は触ってみてください。
https://colab.research.google.com/drive/1rUzL9bFtzFCt3apXkcd81-srSKm61KF1?usp=sharing

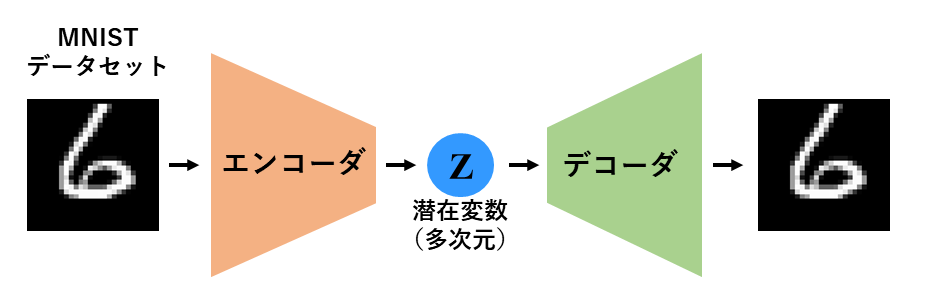
AE（オートエンコーダ）とは

AEはニューラルネットワークを用いた教師無し学習手法の一つであり、エンコーダ-デコーダ構造を有します。
入力データをより少ない次元の変数（潜在変数）で表すことが出来ることから、次元削減・特徴量抽出が可能です。

AE.png

VAEとは

VAEも通常のAEと同様にニューラルネットワークを用いた教師無し学習手法の一つであり、エンコーダ-デコーダ構造を有します。

vae.png

VAEとAEの最大の違いは、潜在変数が正規分布に従うかどうかです。
AEはエンコーダが点推定により潜在変数を導出する為、入力と潜在変数が1対1で対応します。
しかしVAEの潜在変数は正規分布に従う為（同じ入力をしたとしても正規分布に基づき潜在変数の値が変化する）、入力に対して潜在変数が1対1で対応しません。
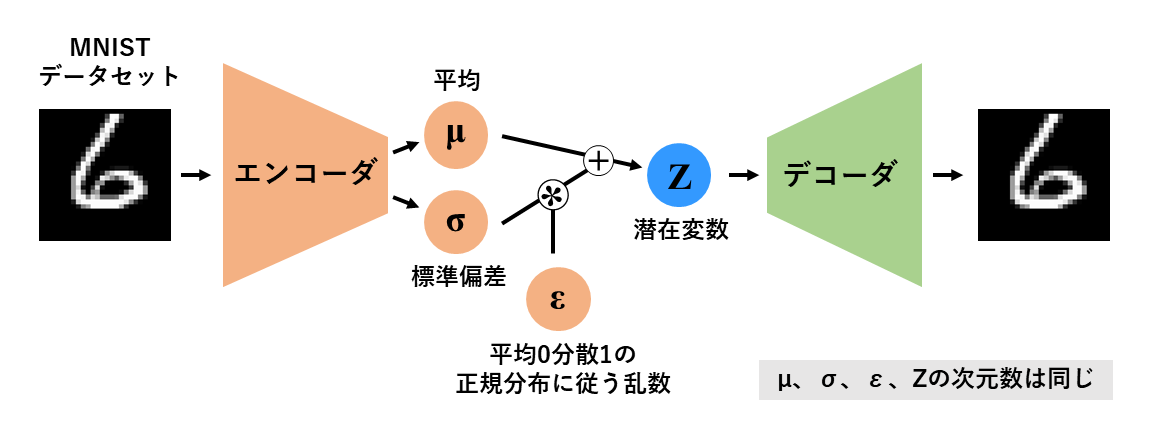
VAEはこの正規分布に従う潜在変数を、再パラメータ化トリックを用いて実現しています。
再パラメータ化トリックは以下の式で表されます。

Z = \mu + \sigma\epsilon

この仕組みにより、ニューラルネットワークモデルによる誤差逆伝播を可能としています。（平均と標準偏差を用いてサンプリングする方法では誤差逆伝播が出来ません。）
また、学習で使用する損失関数も異なります。
通常のAEの損失はクロスエントロピー損失ですが、VAEはこれに潜在変数のばらつきを抑える以下の正則化項が加わります。

\frac{1}{2}\sum_{n=1}^{N} (1 + log((\sigma_{n})^2) - (\mu_{n})^2 - (\sigma_{n})^2)

上述の内容に関する数学的な背景は以下の記事が分かり易いです。
【参考】【徹底解説】VAEをはじめからていねいに
【参考】Variational Autoencoder徹底解説
【参考】VAE (Variational AutoEncoder, 変分オートエンコーダ)
【参考】【超初心者向け】VAEの分かりやすい説明とPyTorchの実装

データセット

MNISTを使用します。
MNISTは手書き数字（1～9）の画像とラベル（画像がどの数字であるか）がセットになったデータセットです。

環境

  • Google Colaboratory Pro

コード

モジュールのimport

import torch
import torch.nn as nn
import torch.nn.functional as F
import torchvision
import torchvision.transforms as transforms
from torch.utils.data import DataLoader
from torchvision.datasets import MNIST, FashionMNIST
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from matplotlib import animation, rc

!apt install imagemagick # gif作成に必要

データセットの作成

pytorchのMNISTデータセットを使用します。
過学習を防ぐ為に全体の20%を検討用データセットとします。

BATCH_SIZE = 100

trainval_data = MNIST("./data", 
                   train=True, 
                   download=True, 
                   transform=transforms.ToTensor())

train_size = int(len(trainval_data) * 0.8)
val_size = int(len(trainval_data) * 0.2)
train_data, val_data = torch.utils.data.random_split(trainval_data, [train_size, val_size])

train_loader = DataLoader(dataset=train_data,
                          batch_size=BATCH_SIZE,
                          shuffle=True,
                          num_workers=0)

val_loader = DataLoader(dataset=val_data,
                        batch_size=BATCH_SIZE,
                        shuffle=True,
                        num_workers=0)

print("train data size: ",len(train_data))   #train data size:  48000
print("train iteration number: ",len(train_data)//BATCH_SIZE)   #train iteration number:  480
print("val data size: ",len(val_data))   #val data size:  12000
print("val iteration number: ",len(val_data)//BATCH_SIZE)   #val iteration number:  120

データの内容は以下の通りです。

images, labels = next(iter(train_loader))
print("images_size:",images.size())   #images_size: torch.Size([100, 1, 28, 28])
print("label:",labels[:10])   #label: tensor([7, 6, 0, 6, 4, 8, 5, 2, 2, 3])

image_numpy = images.detach().numpy().copy()
plt.imshow(image_numpy[0,0,:,:], cmap='gray')

download.png

モデルを作成します。構造はシンプルに3層の全結合型ニューラルネットワークにしています。（リンクを張った冒頭のnotebook内ではこの他にも畳み込み型のモデルを作成したり、FashionMNISTを使用したりしています。）

class Encoder(nn.Module):
  def __init__(self, z_dim):
    super().__init__()
    self.lr = nn.Linear(28*28, 300)
    self.lr2 = nn.Linear(300, 100)
    self.lr_ave = nn.Linear(100, z_dim)   #average
    self.lr_dev = nn.Linear(100, z_dim)   #log(sigma^2)
    self.relu = nn.ReLU()
  
  def forward(self, x):
    x = self.lr(x)
    x = self.relu(x)
    x = self.lr2(x)
    x = self.relu(x)
    ave = self.lr_ave(x)    #average
    log_dev = self.lr_dev(x)    #log(sigma^2)

    ep = torch.randn_like(ave)   #平均0分散1の正規分布に従い生成されるz_dim次元の乱数
    z = ave + torch.exp(log_dev / 2) * ep   #再パラメータ化トリック
    return z, ave, log_dev

class Decoder(nn.Module):
  def __init__(self, z_dim):
    super().__init__()
    self.lr = nn.Linear(z_dim, 100)
    self.lr2 = nn.Linear(100, 300)
    self.lr3 = nn.Linear(300, 28*28)
    self.relu = nn.ReLU()
  
  def forward(self, z):
    x = self.lr(z)
    x = self.relu(x)
    x = self.lr2(x)
    x = self.relu(x)
    x = self.lr3(x)
    x = torch.sigmoid(x)   #MNISTのピクセル値の分布はベルヌーイ分布に近いと考えられるので、シグモイド関数を適用します。
    return x

class VAE(nn.Module):
  def __init__(self, z_dim):
    super().__init__()
    self.encoder = Encoder(z_dim)
    self.decoder = Decoder(z_dim)
  
  def forward(self, x):
    z, ave, log_dev = self.encoder(x)
    x = self.decoder(z)
    return x, z, ave, log_dev

損失関数を定義します。

def criterion(predict, target, ave, log_dev):
  bce_loss = F.binary_cross_entropy(predict, target, reduction='sum')
  kl_loss = -0.5 * torch.sum(1 + log_dev - ave**2 - log_dev.exp())
  loss = bce_loss + kl_loss
  return loss

学習を行います。
潜在変数を2次元に描写したいので、潜在変数を2次元に指定しています。
最適化アルゴリズムはAdamを使用します。

z_dim = 2
num_epochs = 20

device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu") 
model = VAE(z_dim).to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)
scheduler = torch.optim.lr_scheduler.MultiStepLR(optimizer, milestones=[15], gamma=0.1)

history = {"train_loss": [], "val_loss": [], "ave": [], "log_dev": [], "z": [], "labels":[]}

for epoch in range(num_epochs):
  model.train()
  for i, (x, labels) in enumerate(train_loader):
    input = x.to(device).view(-1, 28*28).to(torch.float32)
    output, z, ave, log_dev = model(input)

    history["ave"].append(ave)
    history["log_dev"].append(log_dev)
    history["z"].append(z)
    history["labels"].append(labels)
    loss = criterion(output, input, ave, log_dev)
     
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
     
    if (i+1) % 50 == 0:
      print(f'Epoch: {epoch+1}, loss: {loss: 0.4f}')
    history["train_loss"].append(loss)

  model.eval()
  with torch.no_grad():
    for i, (x, labels) in enumerate(val_loader):
      input = x.to(device).view(-1, 28*28).to(torch.float32)
      output, z, ave, log_dev = model(input)

      loss = criterion(output, input, ave, log_dev)
      history["val_loss"].append(loss)
      
    print(f'Epoch: {epoch+1}, val_loss: {loss: 0.4f}')
  
  scheduler.step()

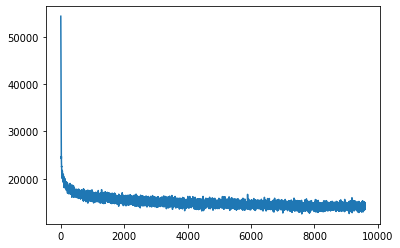
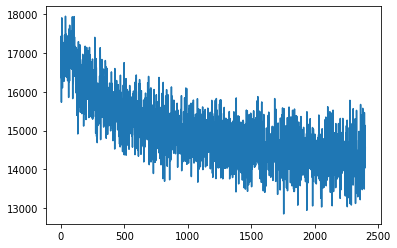
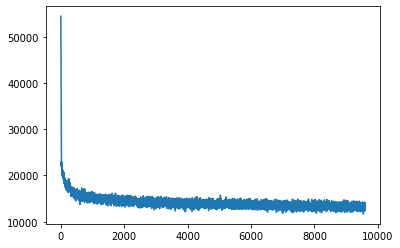
学習用データセットにおける損失の推移をプロットします。

train_loss_tensor = torch.stack(history["train_loss"])
train_loss_np = train_loss_tensor.to('cpu').detach().numpy().copy()
plt.plot(train_loss_np)

vae_train_loss.png

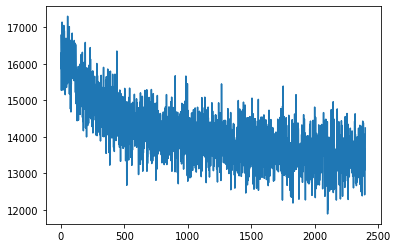
検証用データセットにおける損失の推移をプロットします。
過学習の兆候は認められませんでした。

val_loss_tensor = torch.stack(history["val_loss"])
val_loss_np = val_loss_tensor.to('cpu').detach().numpy().copy()
plt.plot(val_loss_np)

vae_val_loss.png

各学習パラメータの履歴をnumpy配列に変換します。

ave_tensor = torch.stack(history["ave"])
log_var_tensor = torch.stack(history["log_dev"])
z_tensor = torch.stack(history["z"])
labels_tensor = torch.stack(history["labels"])
print(ave_tensor.size())   #torch.Size([9600, 100, 2])
print(log_var_tensor.size())   #torch.Size([9600, 100, 2])
print(z_tensor.size())   #torch.Size([9600, 100, 2])
print(labels_tensor.size())   #torch.Size([9600, 100])

ave_np = ave_tensor.to('cpu').detach().numpy().copy()
log_var_np = log_var_tensor.to('cpu').detach().numpy().copy()
z_np = z_tensor.to('cpu').detach().numpy().copy()
labels_np = labels_tensor.to('cpu').detach().numpy().copy()
print(ave_np.shape)   #(9600, 100, 2)
print(log_var_np.shape)   #(9600, 100, 2)
print(z_np.shape)   #(9600, 100, 2)
print(labels_np.shape)   #(9600, 100)

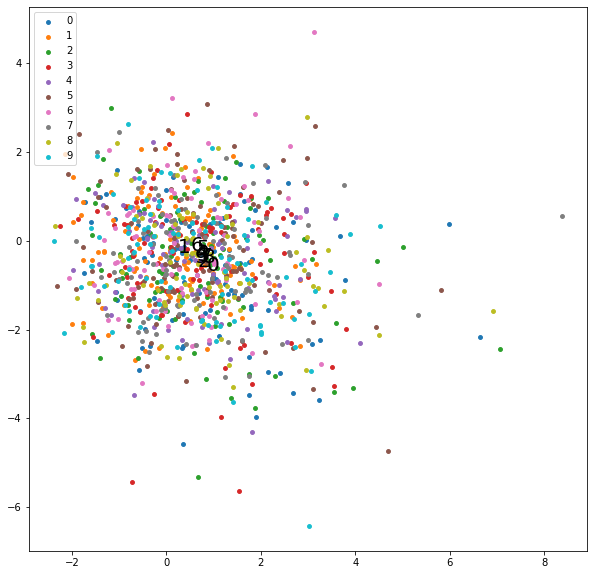
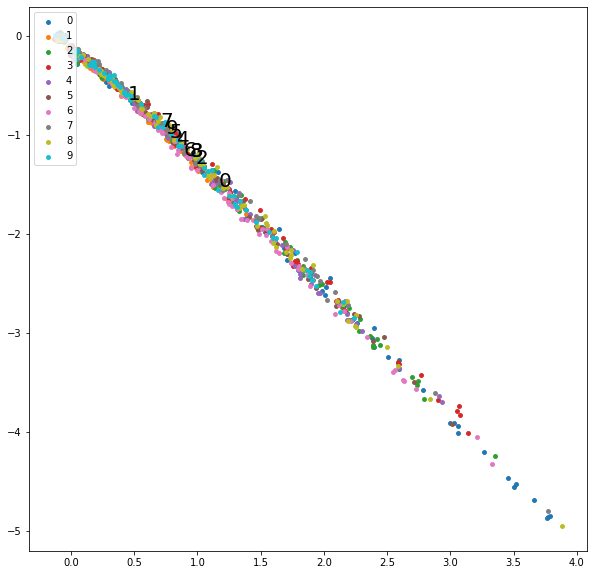
学習序盤の潜在変数の分布をプロットします。
まだバラバラです。

map_keyword = "tab10"
cmap = plt.get_cmap(cmap_keyword)

batch_num =10
plt.figure(figsize=[10,10])
for label in range(10):
  x = z_np[:batch_num,:,0][labels_np[:batch_num,:] == label]
  y = z_np[:batch_num,:,1][labels_np[:batch_num,:] == label]
  plt.scatter(x, y, color=cmap(label/9), label=label, s=15)
  plt.annotate(label, xy=(np.mean(x),np.mean(y)),size=20,color="black")
plt.legend(loc="upper left")

vae_z_20.png

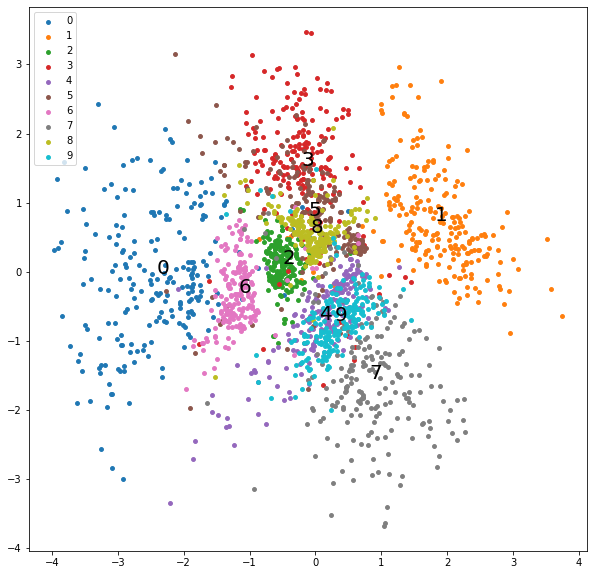
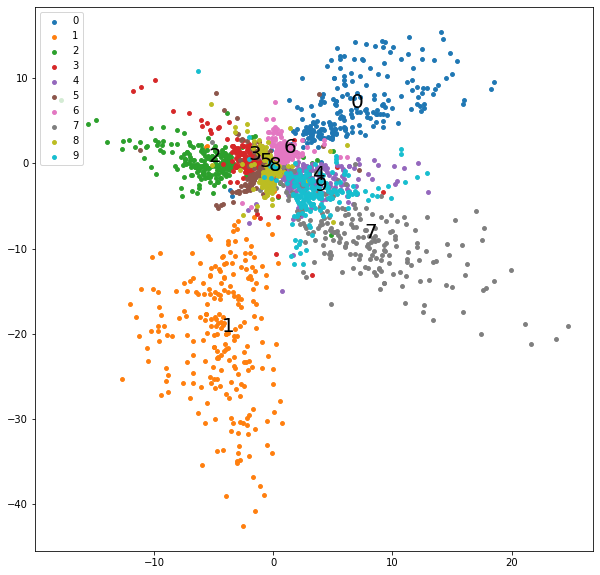
学習終盤の潜在変数の分布をプロットします。
学習が進み、各数字の潜在変数がまとまって存在しています。
黒実線の数字は各数字の潜在変数の平均値に描写しています。
実際には潜在変数は正規分布に従う為、プロットされた点を含む少し大きな円の中にランダムに分布することになります。

batch_num = 9580
plt.figure(figsize=[10,10])
for label in range(10):
  x = z_np[batch_num:,:,0][labels_np[batch_num:,:] == label]
  y = z_np[batch_num:,:,1][labels_np[batch_num:,:] == label]
  plt.scatter(x, y, color=cmap(label/9), label=label, s=15)
  plt.annotate(label, xy=(np.mean(x),np.mean(y)),size=20,color="black")
plt.legend(loc="upper left")

vae_z_9580.png

0の潜在変数の平均値をモデルのデコーダ部に流し込むことで、0の画像を生成します。

model.to("cpu")

label = 0
x_zero_mean = np.mean(ave_np[batch_num:,:,0][labels_np[batch_num:,:] == label])   #x軸の平均値
y_zero_mean = np.mean(ave_np[batch_num:,:,1][labels_np[batch_num:,:] == label])   #y軸の平均値
z_zero = torch.tensor([x_zero_mean,y_zero_mean], dtype = torch.float32)

output = model.decoder(z_zero)
np_output = output.to('cpu').detach().numpy().copy()
np_image = np.reshape(np_output, (28, 28))
plt.imshow(np_image, cmap='gray')

vae_zero.png

0と同様に、1の潜在変数の平均値をモデルのデコーダ部に流し込むことで、1の画像を生成します。

label = 1
x_one_mean = np.mean(ave_np[batch_num:,:,0][labels_np[batch_num:,:] == label])   #x軸の平均値
y_one_mean = np.mean(ave_np[batch_num:,:,1][labels_np[batch_num:,:] == label])   #y軸の平均値
z_one = torch.tensor([x_one_mean,y_one_mean], dtype = torch.float32)

output = model.decoder(z_one)
np_output = output.to('cpu').detach().numpy().copy()
np_image = np.reshape(np_output, (28, 28))
plt.imshow(np_image, cmap='gray')

vae_one.png

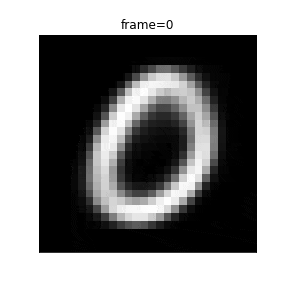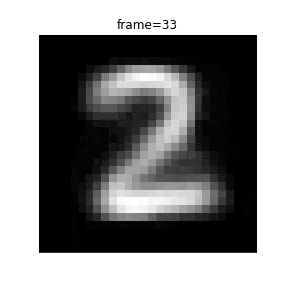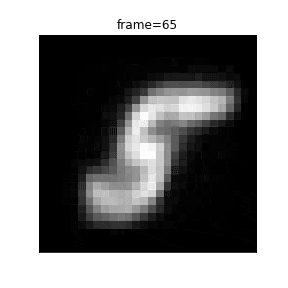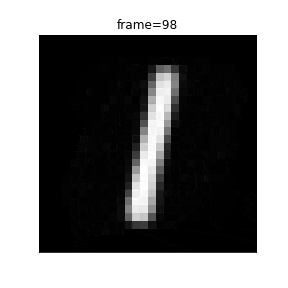
0から1まで潜在変数を移動する際のアニメーションを作成します。

def plot(frame):
    plt.cla()
    z_zerotoone = ((99 - frame) * z_zero +  frame * z_one) / 99
    output = model.decoder(z_zerotoone)
    np_output = output.detach().numpy().copy()
    np_image = np.reshape(np_output, (28, 28))
    plt.imshow(np_image, cmap='gray')
    plt.xticks([]);plt.yticks([])
    plt.title("frame={}".format(frame))

fig = plt.figure(figsize=(4,4))
ani = animation.FuncAnimation(fig, plot, frames=99, interval=100)
rc('animation', html='jshtml')
ani

vae_zerotone (1).gif

以下、VAEではなく通常のAEを作成します。
モデルの構造はVAEとほぼ同じです（再パラメータ化トリックは使用しません）。

class Encoder(nn.Module):
  def __init__(self, z_dim):
    super().__init__()
    self.lr = nn.Linear(28*28, 300)
    self.lr2 = nn.Linear(300, 100)
    self.lr3 = nn.Linear(100, z_dim) #mean
    self.relu = nn.ReLU()
  
  def forward(self, x):
    x = self.lr(x)
    x = self.relu(x)
    x = self.lr2(x)
    x = self.relu(x)
    x = self.lr3(x)
    return x

class Decoder(nn.Module):
  def __init__(self, z_dim):
    super().__init__()
    self.lr = nn.Linear(z_dim, 100)
    self.lr2 = nn.Linear(100, 300)
    self.lr3 = nn.Linear(300, 28*28)
    self.relu = nn.ReLU()
  
  def forward(self, z):
    x = self.lr(z)
    x = self.relu(x)
    x = self.lr2(x)
    x = self.relu(x)
    x = self.lr3(x)
    x = torch.sigmoid(x)
    return x

class VAE(nn.Module):
  def __init__(self, z_dim):
    super().__init__()
    self.encoder = Encoder(z_dim)
    self.decoder = Decoder(z_dim)
  
  def forward(self, x):
    z = self.encoder(x)
    x = self.decoder(z)
    return x, z

損失関数としてバイナリクロスエントロピー関数のみを使用します。

def criterion_ae(predict, target):
  loss = F.binary_cross_entropy(predict, target, reduction='sum')
  return loss

学習を行います。設定はVAEと同じです。

z_dim = 2
num_epochs = 20

device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu") 
model = VAE(z_dim).to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)

history = {"train_loss": [], "val_loss": [], "z": [], "labels":[]}

scheduler = torch.optim.lr_scheduler.MultiStepLR(optimizer, milestones=[15], gamma=0.1)
for epoch in range(num_epochs):
  model.train()
  for i, (x, labels) in enumerate(train_loader):
    input = x.to(device).view(-1, 28*28).to(torch.float32)
    output, z = model(input)

    history["z"].append(z)
    history["labels"].append(labels)
    loss = criterion_ae(output, input)
     
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
     
    if (i+1) % 50 == 0:
      print(f'Epoch: {epoch+1}, loss: {loss: 0.4f}')
    history["train_loss"].append(loss)

  model.eval()
  with torch.no_grad():
    for i, (x, labels) in enumerate(val_loader):
      input = x.to(device).view(-1, 28*28).to(torch.float32)
      output, z = model(input)

      loss = criterion_ae(output, input)
      history["val_loss"].append(loss)
      
    print(f'Epoch: {epoch+1}, val_loss: {loss: 0.4f}')
  
  scheduler.step()

学習用データセットにおける損失の推移をプロットします。

train_loss_tensor = torch.stack(history["train_loss"])
train_loss_np = train_loss_tensor.to('cpu').detach().numpy().copy()
plt.plot(train_loss_np)

ae_train_loss.png

検証用データセットにおける損失の推移をプロットします。
過学習の兆候は認められませんでした。

val_loss_tensor = torch.stack(history["val_loss"])
val_loss_np = val_loss_tensor.to('cpu').detach().numpy().copy()
plt.plot(val_loss_np)

ae_val_loss.png

各学習パラメータの履歴をnumpy配列に変換します。

z_tensor = torch.stack(history["z"])
labels_tensor = torch.stack(history["labels"])
print(z_tensor.size())   #torch.Size([9600, 100, 2])
print(labels_tensor.size())   #torch.Size([9600, 100])

z_np = z_tensor.to('cpu').detach().numpy().copy()
labels_np = labels_tensor.to('cpu').detach().numpy().copy()
print(z_np.shape)   #(9600, 100, 2)
print(labels_np.shape)   #(9600, 100)

学習序盤の潜在変数の分布をプロットします。

z_tensor = torch.stack(history["z"])
labels_tensor = torch.stack(history["labels"])
print(z_tensor.size())
print(labels_tensor.size())

z_np = z_tensor.to('cpu').detach().numpy().copy()
labels_np = labels_tensor.to('cpu').detach().numpy().copy()
print(z_np.shape)
print(labels_np.shape)

map_keyword = "tab10"
cmap = plt.get_cmap(cmap_keyword)

batch_num =10

plt.figure(figsize=[10,10])
for label in range(10):
  x = z_np[:batch_num,:,0][labels_np[:batch_num,:] == label]
  y = z_np[:batch_num,:,1][labels_np[:batch_num,:] == label]
  plt.scatter(x, y, color=cmap(label/9), label=label, s=15)
  plt.annotate(label, xy=(np.mean(x),np.mean(y)),size=20,color="black")
plt.legend(loc="upper left")

ae_z_20.png

学習終盤の潜在変数の分布をプロットします。
学習が進み各数字の潜在変数がまとまって存在していますが、VAEと比較して各軸の最小値-最大値の範囲が広く、ばらつきが大きいことが分かります。

batch_num = 9580

plt.figure(figsize=[10,10])

for label in range(10):
  x = z_np[batch_num:,:,0][labels_np[batch_num:,:] == label]
  y = z_np[batch_num:,:,1][labels_np[batch_num:,:] == label]
  plt.scatter(x, y, color=cmap(label/9), label=label, s=15)
  plt.annotate(label, xy=(np.mean(x),np.mean(y)),size=20,color="black")
plt.legend(loc="upper left")

ae_z_9580.png

0の潜在変数の平均値をモデルのデコーダ部に流し込むことで、0の画像を生成します。

model.to("cpu")

label = 0
x_zero_mean = np.mean(ave_np[batch_num:,:,0][labels_np[batch_num:,:] == label])
y_zero_mean = np.mean(ave_np[batch_num:,:,1][labels_np[batch_num:,:] == label])
z_zero = torch.tensor([x_zero_mean,y_zero_mean], dtype = torch.float32)

output = model.decoder(z_zero)
np_output = output.to('cpu').detach().numpy().copy()
np_image = np.reshape(np_output, (28, 28))
plt.imshow(np_image, cmap='gray')

ae_zero.png

0と同様に、1の潜在変数の平均値をモデルのデコーダ部に流し込むことで、1の画像を生成します。

label = 1
x_one_mean = np.mean(ave_np[batch_num:,:,0][labels_np[batch_num:,:] == label])
y_one_mean = np.mean(ave_np[batch_num:,:,1][labels_np[batch_num:,:] == label])
z_one = torch.tensor([x_one_mean,y_one_mean], dtype = torch.float32)

output = model.decoder(z_one)
np_output = output.to('cpu').detach().numpy().copy()
np_image = np.reshape(np_output, (28, 28))
plt.imshow(np_image, cmap='gray')

ae_one.png

0から1まで潜在変数を移動する際のアニメーションを作成します。

def plot(frame):
    plt.cla()
    z_zerotoone = ((99 - frame) * z_zero +  frame * z_one) / 99
    output = model.decoder(z_zerotoone)
    np_output = output.detach().numpy().copy()
    np_image = np.reshape(np_output, (28, 28))
    plt.imshow(np_image, cmap='gray')
    plt.xticks([]);plt.yticks([])
    plt.title("t={}".format(frame))


fig = plt.figure(figsize=(4,4))
ani = animation.FuncAnimation(fig, plot, frames=99, interval=100)
rc('animation', html='jshtml')
ani

ae_zerotone.gif

MNISTデータセットではVAEと通常のAEの違いが分かりにくいですが、VAEは潜在変数が正規分布に従いランダムに変化するため、エンコーダへの入力がAEと比較して連続的になりやすいです。（損失関数の正則化項の影響もありばらつきにくい。）
従って、各ラベル間に存在する潜在関数からそれなりの画像を生成することが可能であり、（メンテナンス面も含めて）生成モデルとしてはVAEの方が優れていると感じました。

27
20
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
27
20

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?