非連続回帰デザインをベイジアンモデリングする

概要

RDDをベイジアンモデリングで計算する。
〜流れ〜
①補講を受けたかどうかの境界点(60点)を予測させる。
②補講を受けた生徒、受けていない生徒のそれぞれで回帰を行う。

※この記事の内容をベイズにする
https://qiita.com/gekko_datasci/items/b4d5fd1fadf8bc3020f5

データセット

補講授業とテストの点数のデータセット

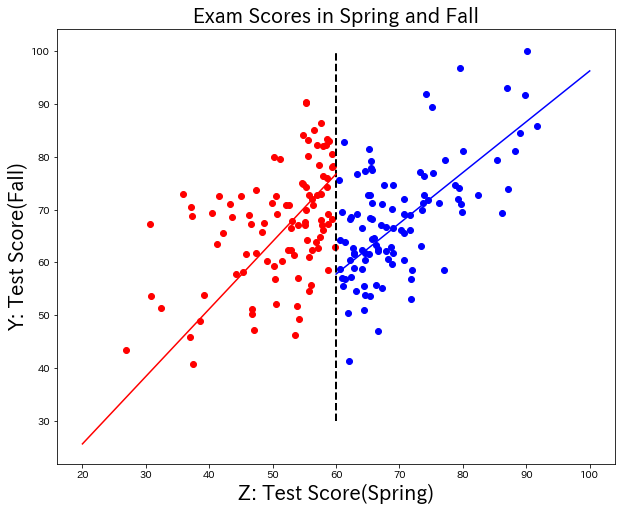
学生のテストの点数(春)と、テストの点数(秋)がある。春のテストの点数が60点以下の生徒は、補講を受けている。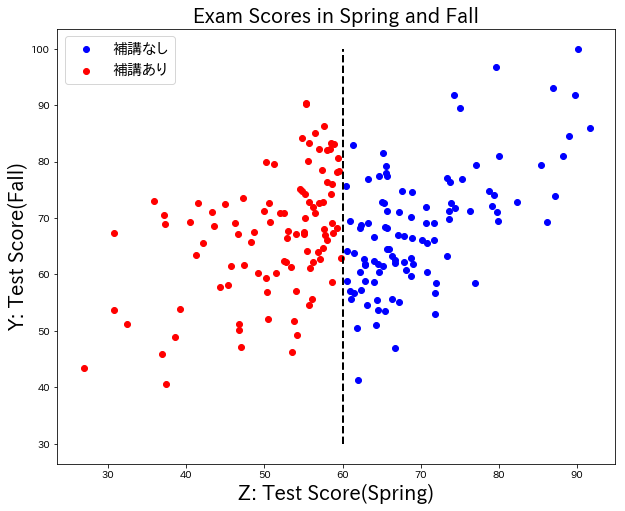

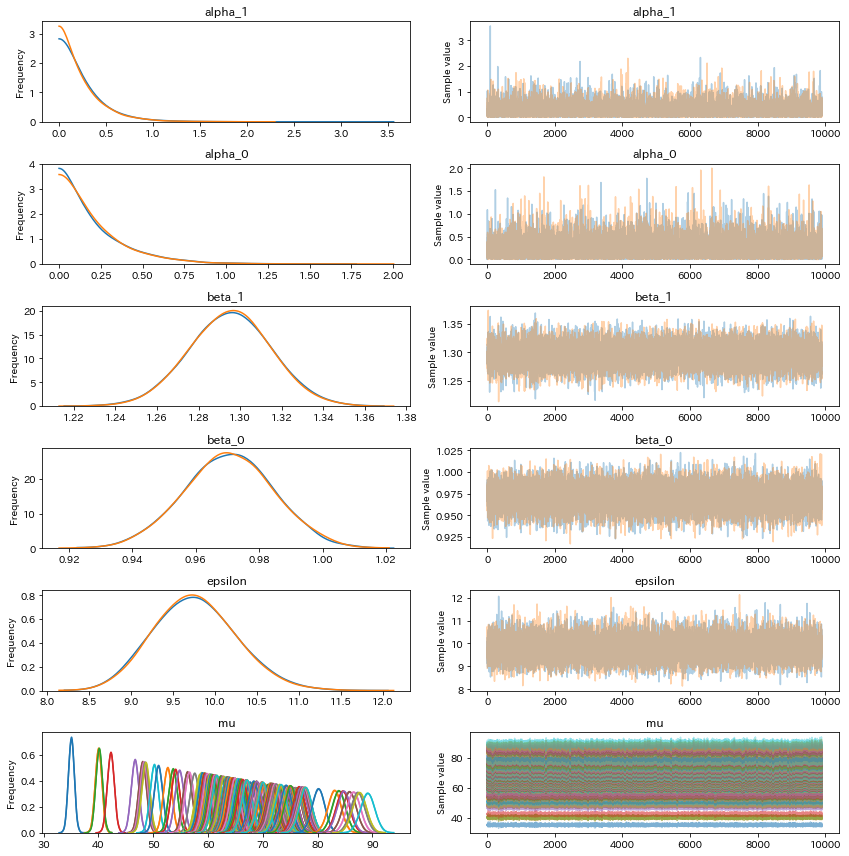
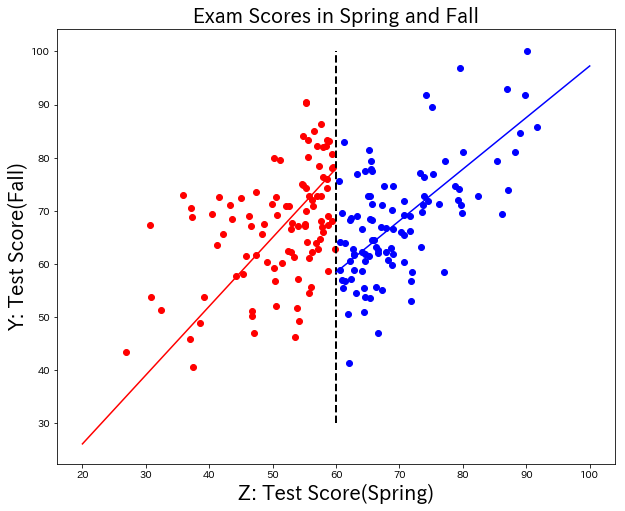
結果①(変化点をあらかじめ教える)

それぞれを単回帰した場合と、だいたい似た結果。
60点での差分は19.51なので、前回の投稿よりも、補講による効果は高く見積もられている。

basic_model = pm.Model()
with basic_model:
    alpha_1 = pm.Exponential('alpha_1', 5)
    alpha_0 = pm.Exponential('alpha_0', 5)
    alpha = pm.math.switch(score_spring < 60, alpha_1, alpha_0)
    beta_1 = pm.Exponential('beta_1', 5)
    beta_0 = pm.Exponential('beta_0', 5)
    beta = pm.math.switch(score_spring < 60, beta_1, beta_0)
    epsilon = pm.HalfCauchy("epsilon", 5)
    mu = pm.Deterministic("mu", alpha + beta * exam_score["Z"])
    observation = pm.Normal('observation', mu=mu, sd=epsilon, observed=exam_score["Y"])

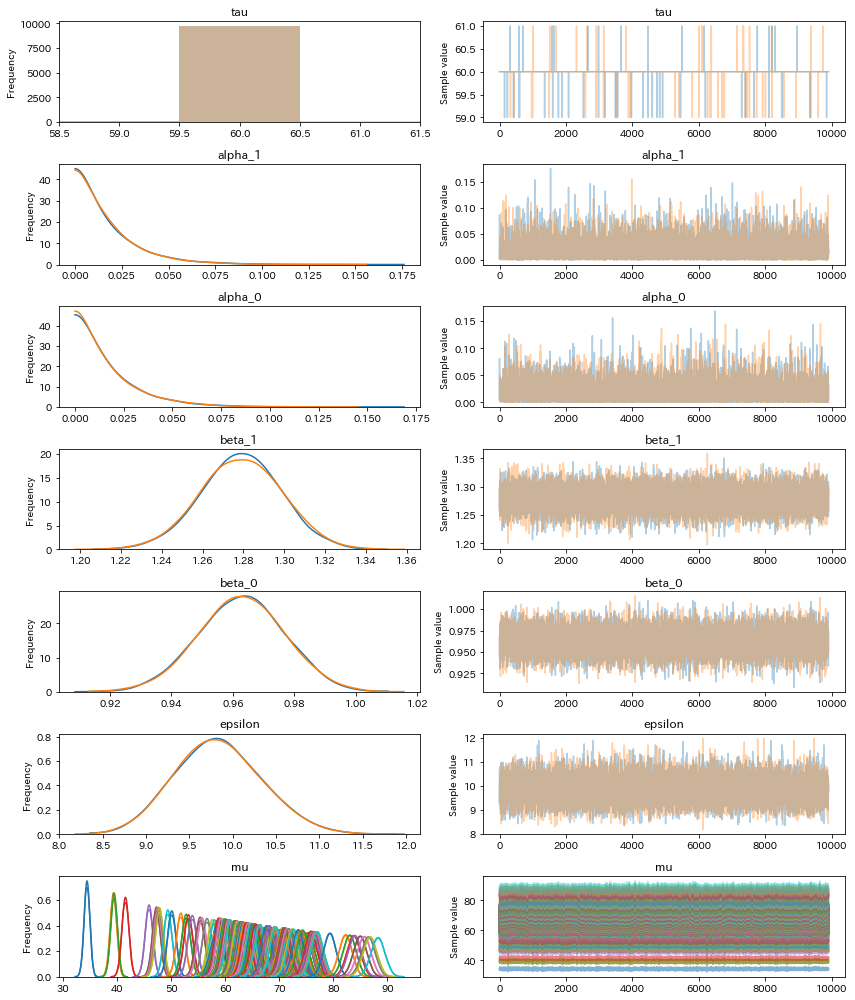
結果②(変化点を教えない)

結果①と同様になった。変化点tauの平均は59.99だったので、変化点も検知できている。
ちなみに、この解析がうまくいくかの肝は、tauの一様分布の区間設定で、[50 - 80]だと今回の結果になるが、[0, 100]くらいにしてしまうと、60点は検出されなかった。

basic_model = pm.Model()

with basic_model:
    tau = pm.DiscreteUniform('tau', lower=50, upper=80)
    alpha_1 = pm.Exponential('alpha_1', tau)
    alpha_0 = pm.Exponential('alpha_0', tau)
    alpha = pm.math.switch(score_spring < tau, alpha_1, alpha_0)
    beta_1 = pm.Exponential('beta_1', tau)
    beta_0 = pm.Exponential('beta_0', tau)
    beta = pm.math.switch(score_spring < tau, beta_1, beta_0)
    epsilon = pm.HalfCauchy("epsilon", 5)
    mu = pm.Deterministic("mu", alpha + beta * exam_score["Z"])
    observation = pm.Normal('observation', mu=mu, sd=epsilon, observed=exam_score["Y"])

コード

import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import pymc3 as pm
import numpy as np
%matplotlib inline

exam_score = pd.read_csv("../Desktop/exam_score.csv")
score_spring = np.array(exam_score["Z"])

#結果１
basic_model = pm.Model()
with basic_model:
    alpha_1 = pm.Exponential('alpha_1', 5)
    alpha_0 = pm.Exponential('alpha_0', 5)
    alpha = pm.math.switch(score_spring < 60, alpha_1, alpha_0)
    beta_1 = pm.Exponential('beta_1', 5)
    beta_0 = pm.Exponential('beta_0', 5)
    beta = pm.math.switch(score_spring < 60, beta_1, beta_0)
    epsilon = pm.HalfCauchy("epsilon", 5)
    mu = pm.Deterministic("mu", alpha + beta * exam_score["Z"])
    observation = pm.Normal('observation', mu=mu, sd=epsilon, observed=exam_score["Y"])

with basic_model:
    trace = pm.sample(10000)

burnin = 100
chain = trace[burnin:]

pm.traceplot(chain)

coef_1 = chain["beta_1"].mean()
coef_0 = chain["beta_0"].mean()
intercept_1 = chain["alpha_1"].mean()
intercept_0 = chain["alpha_0"].mean()
exam_score_0 = exam_score[exam_score["T"] == 0.0]
X_0 = exam_score_0["Z"].reshape(-1, 1)
Y_0 = exam_score_0["Y"].as_matrix()
exam_score_1 = exam_score[exam_score["T"] == 1.0]
X_1 = exam_score_1["Z"].reshape(-1, 1)
Y_1 = exam_score_1["Y"].as_matrix()


x1 = list(range(20, 70, 10))
x0 = list(range(60, 110, 10))
y1 = [coef_1 * i + intercept_1 for i in x1]
y0 = [coef_0 * i + intercept_0 for i in x0]

fig = plt.figure(figsize = (10, 8))
ax = fig.add_subplot(111)
ax.plot(x0, y0, color = "blue")
ax.plot(x1, y1, color="red")
ax.scatter(X_0, Y_0, color="blue")
ax.scatter(X_1, Y_1, color="red")
ax.vlines(60, 30, 100, linestyle='dashed', linewidth=2)
ax.set_ylabel("Y: Test Score(Fall)", fontsize=20)
ax.set_xlabel("Z: Test Score(Spring)",fontsize=20)
ax.set_title("Exam Scores in Spring and Fall", fontsize=20)

print((coef_1 * 60 + intercept_1) - (coef_0 * 60 + intercept_0))

#結果２
basic_model = pm.Model()

with basic_model:
    tau = pm.DiscreteUniform('tau', lower=50, upper=80)
    alpha_1 = pm.Exponential('alpha_1', tau)
    alpha_0 = pm.Exponential('alpha_0', tau)
    alpha = pm.math.switch(score_spring < tau, alpha_1, alpha_0)
    beta_1 = pm.Exponential('beta_1', tau)
    beta_0 = pm.Exponential('beta_0', tau)
    beta = pm.math.switch(score_spring < tau, beta_1, beta_0)
    epsilon = pm.HalfCauchy("epsilon", 5)
    mu = pm.Deterministic("mu", alpha + beta * exam_score["Z"])
    observation = pm.Normal('observation', mu=mu, sd=epsilon, observed=exam_score["Y"])

with basic_model:
    trace = pm.sample(10000)
burnin = 100
chain = trace[burnin:]

pm.traceplot(chain)

coef_1 = chain["beta_1"].mean()
coef_0 = chain["beta_0"].mean()
intercept_1 = chain["alpha_1"].mean()
intercept_0 = chain["alpha_0"].mean()
exam_score_0 = exam_score[exam_score["T"] == 0.0]
X_0 = exam_score_0["Z"].reshape(-1, 1)
Y_0 = exam_score_0["Y"].as_matrix()
exam_score_1 = exam_score[exam_score["T"] == 1.0]
X_1 = exam_score_1["Z"].reshape(-1, 1)
Y_1 = exam_score_1["Y"].as_matrix()


x1 = list(range(20, 70, 10))
x0 = list(range(60, 110, 10))
y1 = [coef_1 * i + intercept_1 for i in x1]
y0 = [coef_0 * i + intercept_0 for i in x0]

fig = plt.figure(figsize = (10, 8))
# FigureにAxesを１つ追加
ax = fig.add_subplot(111)
ax.plot(x0, y0, color = "blue")
ax.plot(x1, y1, color="red")
ax.scatter(X_0, Y_0, color="blue")
ax.scatter(X_1, Y_1, color="red")
ax.vlines(60, 30, 100, linestyle='dashed', linewidth=2)
ax.set_ylabel("Y: Test Score(Fall)", fontsize=20)
ax.set_xlabel("Z: Test Score(Spring)",fontsize=20)
ax.set_title("Exam Scores in Spring and Fall", fontsize=20)

print(chain.tau.mean())

感想

ベイズ面白い。他にもいろいろ出来そう。

参考ページ

Rで回帰分断デザイン
https://qiita.com/saltcooky/items/b7cb016498d2dd7b327e