はじめに
岩波書店の確率と情報の科学シリーズの星野崇宏 著「調査観測データの統計科学」を読んでいき、まとめていってます。
1章 「調査観測データの統計科学(1)」
2章 「調査観測データの統計科学(2)」
3章A 「調査観測データの統計科学(3)」
3章B 「調査観測データの統計科学(二重にロバストな推定/操作変数法)」
今回は、前回の続きで第3章「セミパラメトリック解析」で「回帰分断デザイン」と「DID推定」についてです。
回帰分断デザイン
処置群に割り当てるかが、ある一つの変数$x$が閾値$c$以上であるかどうかで決まる場合があります
。
例えば、特定の教育プログラムを受けるかどうかが、テストの点数が一定以上である場合のようなものが代表的です。
このような研究デザインを、回帰分断デザイン(Regression Discountinuity Design)とよばれています。
この時、閾値$c$の周辺のサンプルにおいて、$c$以上になるか=処置群にあるかはノイズの影響によりランダムに決定されると考えられます。
そのため、強く無視できる割り当て条件が成立していると言えます。
これまでと同様に潜在的な結果変量$(y_1,y_0)$を考えます。
y=y_1z+y_0(1-z)
結果変量を仮定した、回帰分断デザインにおける処置群と対照群の差は次にように表現できます。
E(y|x,z=1)-E(y|x,z=0)=E(y_1|x,z=1)-E(y_0|x,z=0)\\
=\{E(y_1|x,z=1)-E(y_0|x,z=1)\}+\{E(y_1|x,z=1)-E(y_0|x,z=0)\}
1段目は、潜在的な結果変量における回帰関数の差であることを意味しています。
2段目は、「処置群における潜在的な結果変量についての回帰関数の差」と「対照群に割り当てられた場合に得られる結果変数$y_0$の回帰関数の差」に分解できることを意味しています。
これは、介入を説明変数として一つの回帰式で表現することもできます。
しかしこの場合、介入群と非介入群で回帰モデルの傾きが等しいことを仮定しています。
実際には介入により傾きが変化してしまう場合もあります。
そのため、閾値$c$前後でデータを分け、それぞれで回帰モデルを作成します。
それぞれの回帰モデルで、$x=c$の場合の結果変数$y$を推定し、その差が介入効果となります。
また、次のように閾値$c$で$Z$を中心化して説明変数を用いることで、1つの回帰モデルで二つの傾き時の状態を表現できます。
Y = α_0 + τ・Z + β_1・Z(X - c) + β_0・(1-Z)(X - c) + ε
ここで、$τ$は処置による効果、$α_0$は切片、$β_0$と$β_1$は各群を表現する回帰式おける係数です。
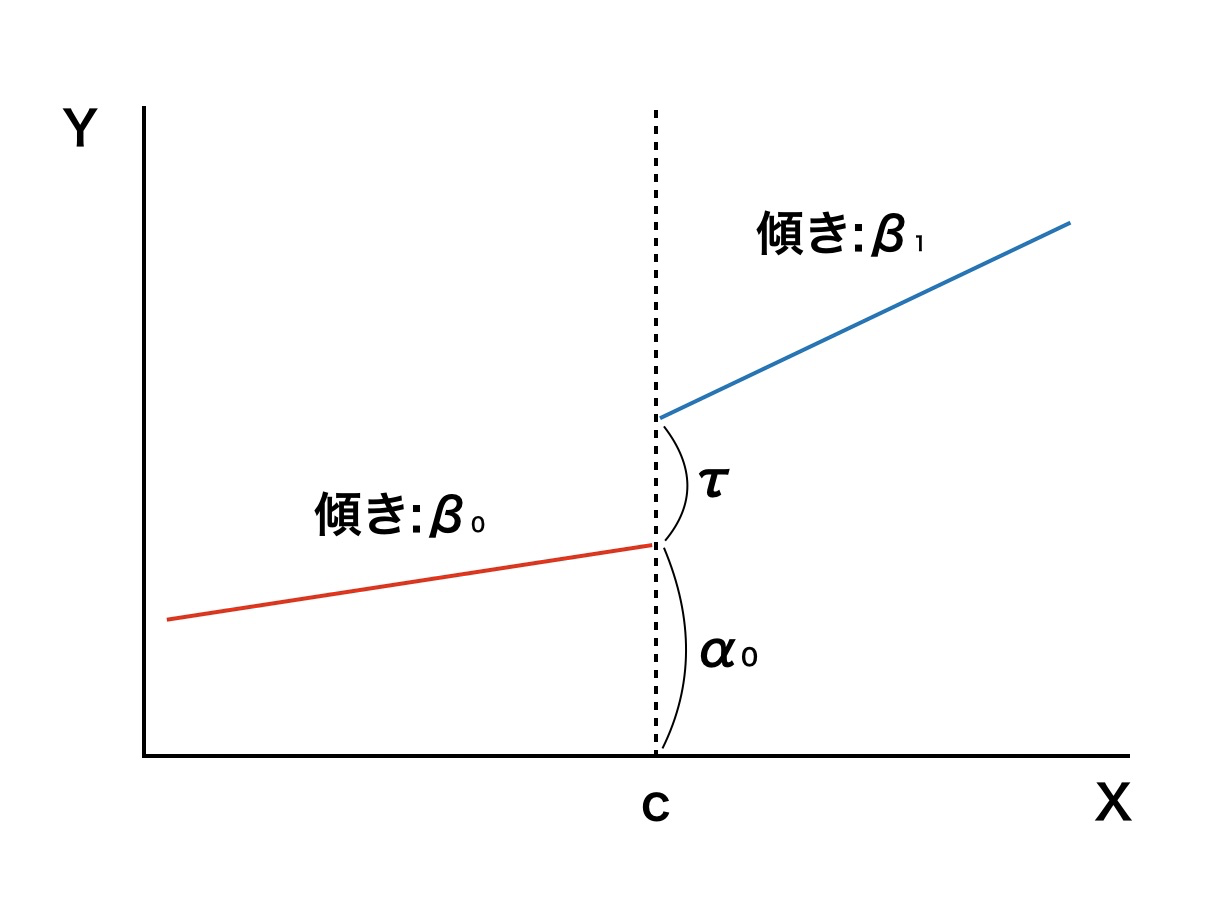
$Z=1$の場合、切片が$(α_0 + τ)$、傾きが$β_1$の回帰式(青線)が得られます。
Y = (α_0 + τ) + β_1(X - c) + ε
$Z=0$の場合、切片が$α_0$、傾きが$β_1$の回帰式(赤線)が得られます。
Y = α_0 + β_0(X - c) + ε
RでRDD
用いたデータは、こちらのページから拝借されてもらった、試験のデータです。
$x$が前期試験であり、60点以下の学生には補講を実施しています。
そして、後期試験の得点を結果変量として補講の効果の推定を行いました。
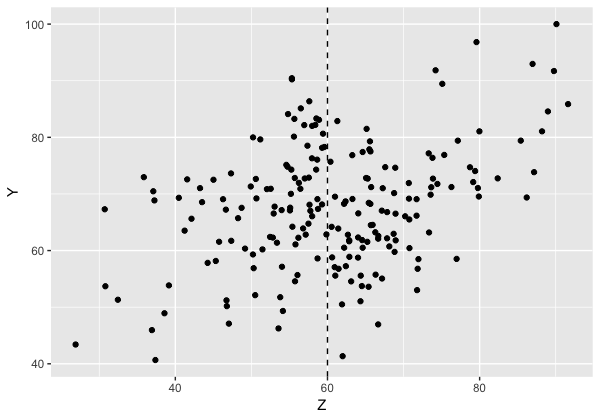
はじめに、データを読み込んで可視化してみます。
library(tidyverse)
library(readr)
exam <- read_csv("exam.score.csv")
ggplot(exam, aes(x = Z, y = Y)) +
geom_point() +
geom_vline(xintercept= 60, linetype = 2)
# 閾値前後のそれぞれデータを利用した回帰モデルを作成
model1 <- lm(Y ~ Z, data = exam %>% filter(Z < 60))
model2 <- lm(Y ~ Z, data = exam %>% filter(Z > 60))
# それぞれの群におけるxが最大最小,60の時の値をまとめておきます
Z1.range <- c(min(exam$Z), 60)
Z2.range <- c(60, max(exam$Z))
# 作成した回帰モデルでxが最大最小,60の時の結果変数を求めます
fitY1 <- predict(model1, newdata = data.frame(Z = Z1.range))
fitY2 <- predict(model2, newdata = data.frame(Z = Z2.range))
推定された結果を見てみます。
> fitY1
1 2
51.23442 73.10664
> fitY2
1 2
60.06645 86.17521
そして、処置効果の算出です。
> # 効果を算出
> fitY1[2] - fitY2[1]
1
13.04019
補講の効果は13点であったといえます。
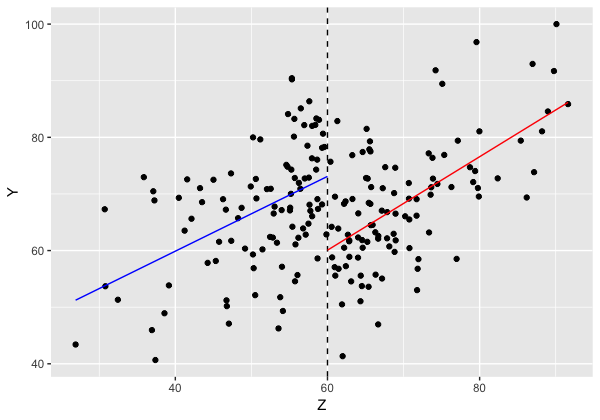
どれぐらいの違いなのかを可視化してみます
# 回帰直線を引いてみる
ggplot(exam, aes(x = Z, y = Y)) +
geom_point() +
geom_vline(xintercept= 60, linetype = 2) +
geom_line(data = line1, aes(x=Z,y=Y),
stat="identity", position="identity",
colour="blue") +
geom_line(data = line2, aes(x=Z,y=Y),
stat="identity", position="identity",
colour = "red")
次に、一つの回帰分析式で処理効果を見てみたいと思います。
# 一つの回帰式で考える
exam <- exam %>%
mutate(x2 = T*(Z-60),
x3 = (1-T)*(Z-60))
fit_reg <- lm(Y ~ T + x2 + x3, data = exam)
> summary(fit_reg)
Call:
lm(formula = Y ~ T + x2 + x3, data = exam)
Residuals:
Min 1Q Median 3Q Max
-22.6094 -5.7117 -0.6302 5.8505 21.7367
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 60.0665 1.4556 41.266 < 2e-16 ***
T 13.0402 2.0336 6.412 1.05e-09 ***
x2 0.6606 0.1214 5.444 1.55e-07 ***
x3 0.8256 0.1154 7.153 1.65e-11 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 9.131 on 196 degrees of freedom
Multiple R-squared: 0.2935, Adjusted R-squared: 0.2826
F-statistic: 27.13 on 3 and 196 DF, p-value: 1.011e-14
Tの係数が補講による効果であり、一つ目の算出方法と等しい値を得られました。
また、介入群のほうが傾きが大きいようです。
差分の差(DID)推定量
介入群と対象群では、観測値の性質が大きく異なることがある。
例えば、ある教育プログラム効果を推定したいと考えます。
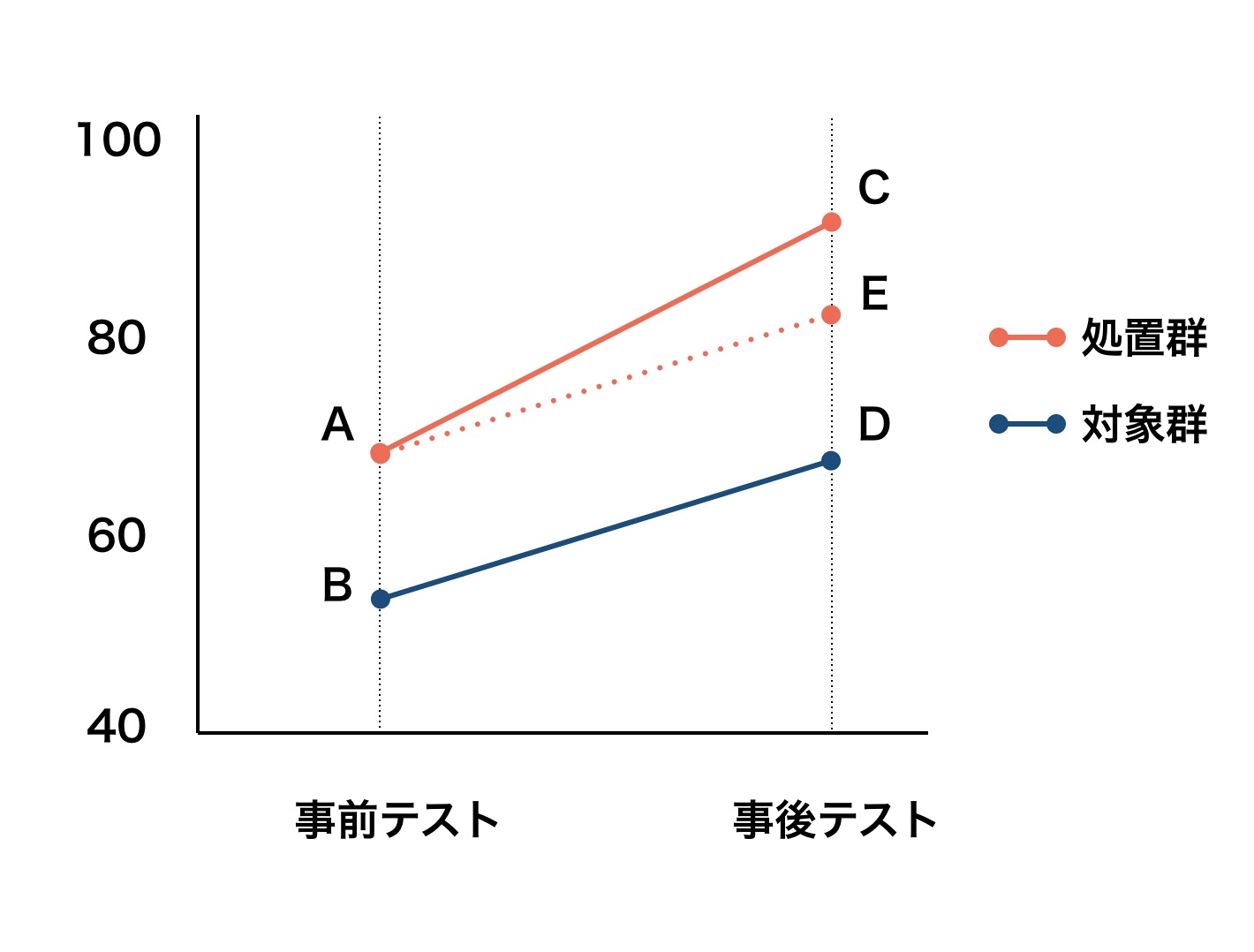
プログラムを受けた群と受けなかった群での、事前テスト/事後テストの群平均を次のグラフにあらわしました。
一般には、処置群の事前テストと事後テストの平均点数を比較する$(C-A)$を求めることが多いです。
しかし、処置に関係なく事前テストと事後テストに差が生まれてしまうことがあります。
例えば、全ての対象者に同一の授業を行った影響であったり、テストの難易度が変化したりする様なことがあげられます。
そのため、$(C-A)$では純粋な処置の効果を推定することはできません。
この差は処置以外で生じた効果といえます。
対象群における事後テストと事前テストの差分$(D=B)$が処置以外で生じた効果といえます。
DID = C-E=(C-A)-(D-B)
この様に、処置群の差と対照群の差の差をより求める推定量をDID(difference in defference)推定量と呼びます。
これまでと同じように潜在的な結果変量を使って少しフォーマルに説明にします。
- $y_{1b}$は「もし処置対象となる集団に属していない場合における」処置実施ごの結果変量の値
- $y_{0b}$は「もし処置対象となる集団に属した場合における」処置実施ごの結果変量の値
- $y_a$は、施策を実施する前の結果変量の値
t時点でのグループへの所属のインディケータ$z$を利用します。
b時点で実際に得られる従属変数$y_b$は、2つの潜在的な結果変数$y_{1b}$、$y_{0b}$ち$z$を組み合わせで次の様に表現できます。
y_b=zy_{1b}+(1-z)y_{0b}
観測値$y$はこれらの変数を用いて次の様に表現できます。
y=\delta y_b+(1-\delta)y_a = \delta {zy_{1b}+(1-z)y_{0b}}+(1-\delta)y_a
ここで、$\delta$は, $\delta=1$であればb時点での観測値、$\delta=0$であればa時点での測定値を意味するインジケータです。
そして、これらの変数を用いて、DIDを定義すると次の様になります。
DID = {E(y|z=1,\delta=1)-E(y|z=1,\delta=0)}-{E(y|z=0,\delta=1)-E(y|z=0,\delta=0)}\\
= E(y_{1b}-y_a|z=1)-E(y_{0b}-y_a|z=0)
$E(y_{1b}-y_a|z=1)$は、処置による影響と処置以外の影響を表現しており、$E(y_{0b}-y_a|z=0)$は、(対象群での)処置以外の影響を表現を表現している。
この推定が行えるためには、処置以外の影響が2群において等しいという、平行トレンド仮定が成り立っていることが必要です。
この仮定は、現実では成り立たないことが多いです。
そのため、処置以外の影響を説明変数により説明することで、並行トレンド仮定を成り立ちやすくします。
RでDID推定量の算出
ここから取得できるプリンストン大学で提供されているデータを使いしました。
7カ国の1990年から1999年のパネルデータであり、1994年にE,F,Gの国で何かしらの変化があった様です。
(データセットの説明を見てもどんな変化なのかがよくわかりませんでした。)
その変化の効果を推定したいと思います。
panel = read.dta("https://dss.princeton.edu/training/Panel101.dta")
データの中身を確認してみます。
> head(panel)
country year y y_bin x1 x2 x3 opinion
1 A 1990 1342787840 1 0.2779036 -1.1079559 0.28255358 Str agree
2 A 1991 -1899660544 0 0.3206847 -0.9487200 0.49253848 Disag
3 A 1992 -11234363 0 0.3634657 -0.7894840 0.70252335 Disag
4 A 1993 2645775360 1 0.2461440 -0.8855330 -0.09439092 Disag
5 A 1994 3008334848 1 0.4246230 -0.7297683 0.94613063 Disag
6 A 1995 3229574144 1 0.4772141 -0.7232460 1.02968037 Str agree
今回は、yを評価に用いる変数とています。
少しデータを加工します。
# 処置の国と時期フラグを作成
panel_df <- panel %>%
mutate(postperiod = if_else(year >= 1994, 1, 0),
treated = if_else(country %in% c("E", "F", "G"), 1, 0))
# 1993年と1994年のデータを抽出
panel_df2 <- panel_df %>%
group_by(country) %>%
filter(row_number() %in% c(4,5))
# 処置群と対照群で平均値を算出
panel_matrix <- panel_df2 %>%
group_by(postperiod,treated) %>%
summarise(score = mean(y))
グラフを作成して変化を確認してみました。
介入群の方が増加率が低いようです。
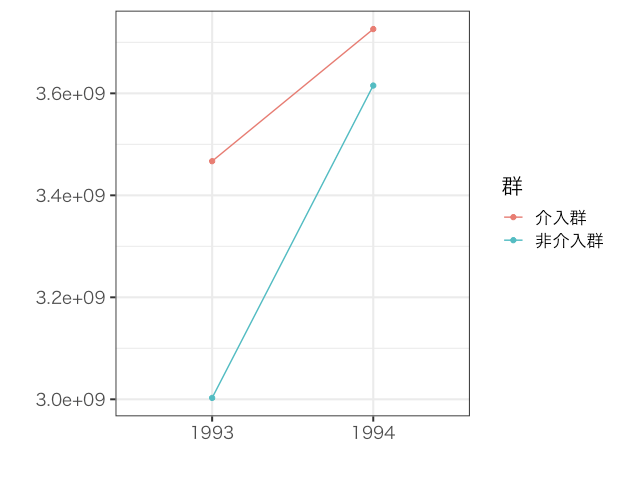
一般的な処置の効果$E(y_{1b}-y_a|z=1)$を計算してみます。
> # 一般的な影響を算出
> diff_TG = panel_matrix$score[4] - panel_matrix$score[2]
> diff_TG
[1] 259074043
$E(y_{0b}-y_a|z=0)$も算出して、DID推定量を計算しました。
> diff_NTG = panel_matrix$score[3] - panel_matrix$score[1]
> DID = diff_TG - diff_NTG
> DID
[1] -353480357
符号が逆転していますね。DID推定量を求めない場合、正しくない結論を導いてしまう可能性があると考えられます。
以上です。
次回は、第4章の「共変量選択と無視できない欠測」です。