少しは真面目に、因果推論等を勉強しようと思いました。
岩波書店の確率と情報の科学シリーズの星野崇宏 著「調査観測データの統計科学」を読んでいき、まとめたいと思います。
時折、サンプルデータを利用して実装検証していきます。
第1章 序論
実験できない場合に因果関係を推論するとは?
ある2つの変数の変数の因果関係を見る場合には、原因となる変数を直接操作することができる。
一方、社会科学の分野では、原因となる変数を操作することができない場合も多い。
例えば、早期英語教育の効果を知りたい場合に、子供に早期英語教育を受けさせる親は、学歴が高く、英語教育にも力を入れている。
そして、子供の知能が高いなどの複雑な要因が関わっていると考えられる。
これらの要因(変数)は偏りがある場合が多く、コントロールしてデータを網羅的に取得することはできない。
実験群と対照群の各群の対象者をランダムに割り振ることのできない調査観測研究は、無作為割り当てが行えない調査観測研究と呼ぶ。
このような研究では、それぞれの群への割り当てや効果変量に影響を与える様々変数の影響を除去しなければ、2群の本来の差=目的の変量の効果を知ることはできない。
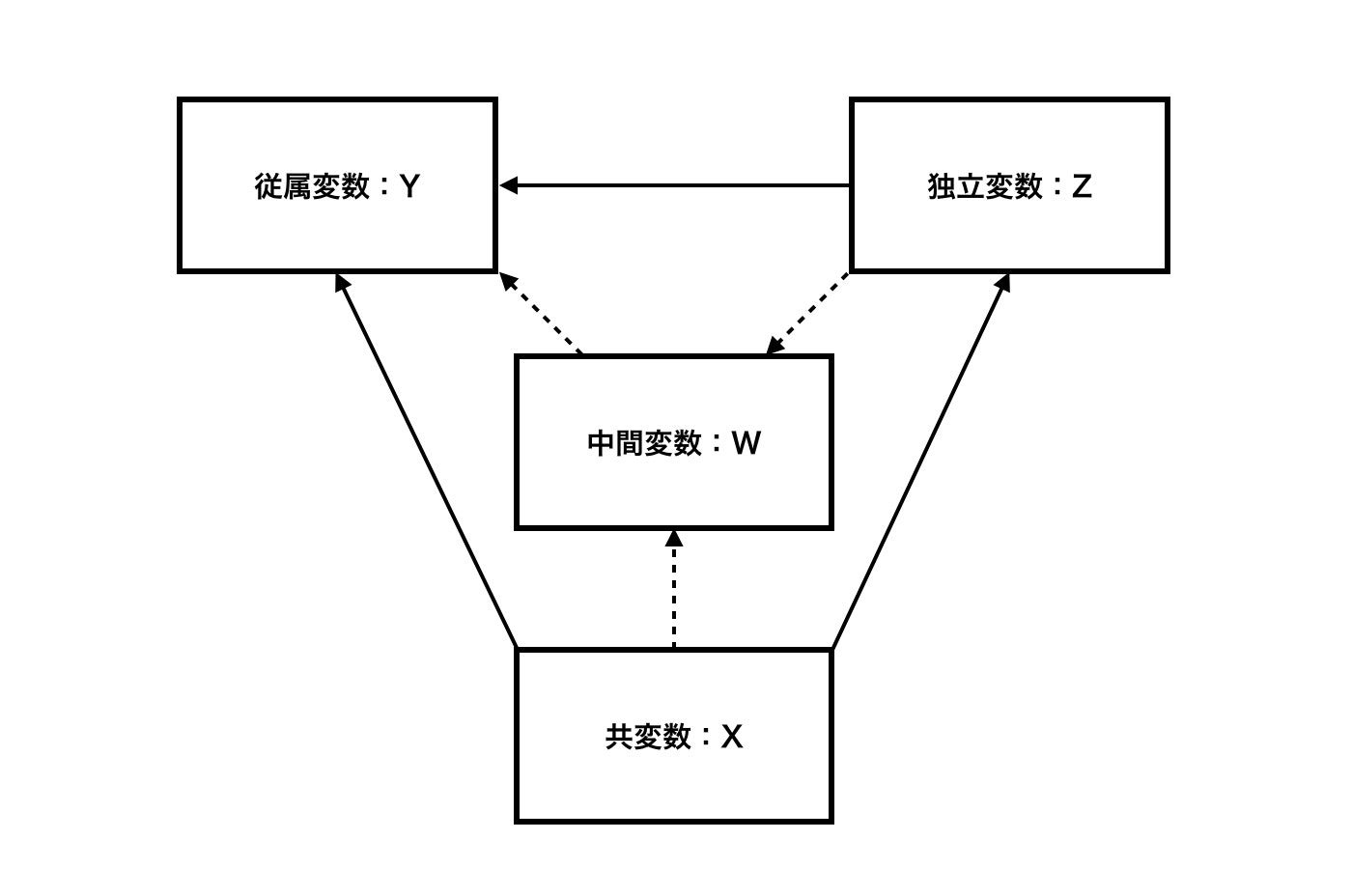
実験研究と調査観測研究
・従属変数(dependent variable)
結果となる変数。効果変数や基準変数とも呼ばれる。
例:20歳における英語の習得度
・独立変数(independent variable)
原因となる変数。説明変数、予測変数とも呼ばれる。
早期教育を行なっていたか、
・共変量(covariate)
従属変数と独立変数に影響を与える変数。統制変数、交絡因子、交絡要因とも呼ばれる。
・中間変数(intermediate variable)
独立変数と従属変数の間に介在し、独立変数から影響を受けて従属変数に影響を与える変数。
媒介変数と呼ばれる。
実験研究とは、独立変数を操作して、従属変数がどのように変化するのかを調べる研究。
調査観測研究は、無作為割り当てを伴わない研究。
因果関係の推定の例
因果効果を無作為割り当てを行なった場合の処置群と対照群の差であると定義した際の例をあげている。
妊娠中の母親の喫煙が子供の知能に影響を与えるのかを調査したアメリカの研究が存在する。
この研究では、妊娠中に喫煙した母親の子供とそうでない子供の数学と読解力に関する得点を比較することにより影響を考えている。
その結果、非喫煙群と喫煙群の間で有意な差があると考えられた。
しかし、母親の妊娠中の喫煙以外にも、飲酒や学歴といった様々な共変量で子供の知能発達は影響を受ける。
そのため、これら共変量を除去して、「妊娠中に喫煙する群と喫煙しない群に無作為割り当てを行なった場合の結果」を推定する必要がある。
母親の年齢、人種、就業状況、使用言語等の10変数を利用して、非喫煙群と喫煙群の判別をロジスティック回帰分析を用いて行なった。
この結果を用いて、傾向スコアと呼ばれる共変量の影響を除く値を取得し、無作為割り当てに近い状態に調整する。
この操作により得られた、調整済みの非喫煙群と喫煙群において、読解力には有意な差が存在したが、数学では有意な差はないことがわかった。
このように、共変量の影響を除くことにより独立変数と従属変数の因果効果を推定することに繋がる。
バイアスのある調査データの例
選択バイアスとは、研究対照群かある一部の対象者を選択し、分析を行うことで生じる歪みである。
家計における教育費の割合を調査した。
この調査では、「国の教育ローンを利用している世帯」に対する、世帯収入における教育費は平均34.1%であった。
また、年収が200万円以上400万円未満の家庭では、世帯収入の55.6%に達していた。
教育費の負担が非常に重いという印象を受ける。
しかし、高校以上の学校に進学している子供がいて、国の教育ローンを利用している家庭の多くが高い教育費を払っている家庭である。
この調査は、教育費が家計に重くのしかかる世帯に対して収入に占めている教育費の割合を調査している。
そのため、必然的に高校以上の子供がいる家庭全体の調査よりも、教育費の割合が高くなる。
対象母集団から、実験のためにデータを取得する時点で、母集団を代表していないという偏り(バイアス)が出てしまう。
このような選択バイアスは、ノーベル経済学賞を受賞したヘックマンの一連の研究以降、様々な分野で人間が自主的に行動選択するタスクでの解析では、考慮すべき重要な問題となっている。
因果推論・選択バイアス・データ集合の統一的理解
調査観測研究での因果推定を欠測データの問題として扱う。
もし介入を受け入れた場合の従属変数の値と$y_i$、もし介入を受けなかった場合の従属変数の値を$y_0$と考える。
観測さてるのは、一方のみであり、もう一方は観測されない。
そして、それらとは別に全対象者に共通している共変量を取得していると考えられる。
近年の社会科学では、統計的因果推論に関する問題は、この欠測データの問題を共変量を用いて解決するという枠組みが用いられている。
しかし、共変量を用いた統計的調整法は難点がいくつか存在している。
従属変数と共変量の非線形な関係をうまく表現できず、調整ができない。
共変量が多くなると、次元の呪いが起こる場合がある。
これらの問題に対して、様々な解決策が考えらている。

選択バイアスが存在するデータに対しても、この欠測データと共変量情報の枠組みの問題と考えることができる。
関心のある従属変数は回答群では観測できるが、非回答群では観測できない。
非回答のデータとは、欠測データであると考えることができる。
そのため、共変量情報で補正することにより、選択バイアスの議論を行うことができる。

欠測データと共変量の枠組みは、調査観測研究以外の課題に対しても適用することができる。
ECサイト等では、ページ閲覧履歴や購買データと、サイト以外での市場調査データをリンクさせてデータ分析を行う必要性がある。
しかし、多くの場合に一方のデータしか集まらない。
その際に、対象者の異なる複数の情報源のデータを統合して、同一の対象が全ての市場調査を受けてるデータ・シングルソースデータを構成する。
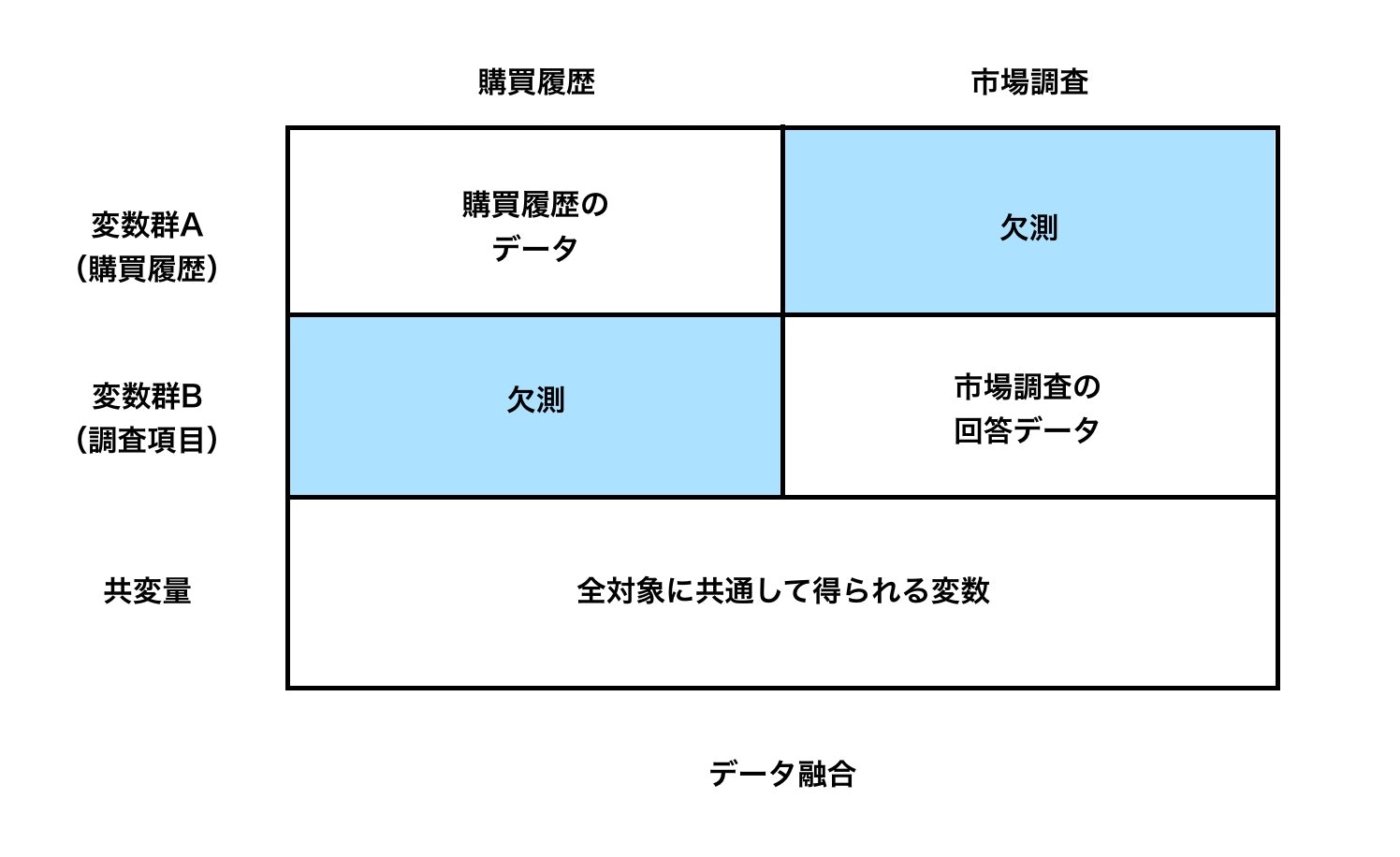
これはデータフュージョンと呼ばれ、ビデオリサーチ社等で実施され成果をあげている。
データフュージョンを行う際には、Aの市場調査で得られてる変数群とBの市場調査で得られてる変数群が存在し、背反関係にあり、一方で得られた変数が得られた対象はもう一方での調査では変数を得られていない。
そして、AB両方で得られている共変量が存在する。
この共変量とAの変数群$X_a$を因子分析や主成分分析にかけて得られて因子や主成分を利用して、Bの変数群$X_a$を予測する方法がよく利用される。
1章まとめ
このように、「調査観測データでの因果推定」「選択バイアス」「データ融合」では、基本的に欠測データという同じ枠組みで考えていくことができる。
その基本戦略は、
- 欠測のあるデータの枠組みで考える
- 共変量を積極的に集め、活用する
- セミパラメトリックな手法を用いてロバストな結果を得る。
2章では、「調査観測データでの因果推定」を取り上げる。