Pythonで学ぶ統計検定2級の確率分布①

はじめに

統計検定の勉強をしていると様々な確率分布が出てきますが、数式だけ見ても中々イメージが付きにくいと思います。Pythonで色々パラーメータを動かしながら確率分布を描画してそのイメージをつけていきます。

参考

確率分布の説明については下記を参考にしています。

• 統計学の時間
• 統計学入門 (基礎統計学Ⅰ) 東京大学教養学部統計学教室

様々な確率分布

本記事では各種数式の導出等の細かな説明は行わず、各分布の形とその分布が意味することのイメージを掴むことを主眼においています。この記事では下記2つの分布を扱います。

• 二項分布
• ポアソン分布

二項分布

「コインを投げたときに表が出るか裏が出るか」のように起こる結果が2つしかない互いに独立した試行(ベルヌーイ試行)を$n$回行なって成功する回数$X$が従う分布を二項分布と呼びます。

• サイコロを10回振って1が出る回数
• コインを5回投げた時に表が出る回数
• 勝率7割の野球チームが144試合を実施して勝利する回数

などが二項分布に従います。

二項分布の確率質量関数の数式は下記のように表されます。

P(X = k) = {}_n C _kp^k(1-p)^{n-k}

$n$は試行回数、$p$はその試行の成功確率、$k$はその試行が成功した回数です。

また確率変数$X$が二項分布に従う時、の期待値$E(X)$と分散$V(X)$は以下のようになります。

E(X) = np

V(X) = np(1 - p)

試行回数$n$とその成功確率$p$を掛け合わせたものが期待値になっているのは感覚とも合致するかと思います。

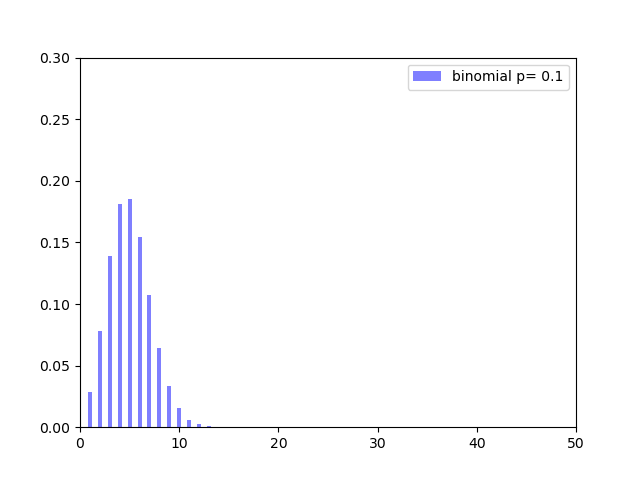
ではPythonで確率分布を描画してみます。成功確率$10\%$の試行を$50$回実施した時、その成功回数はどのような分布になるかを確認します。

import numpy as np
import matplotlib.pyplot as plt

fig = plt.figure()

def comb_(n, k):
    result = math.factorial(n) / (np.math.factorial(n - k) * np.math.factorial(k))
    return result


def binomial_dist(p, n, k):
    result = comb_(n, k) * (p**k) * ((1 - p) ** (n - k))
    return result

x =  np.arange(1, 50, 1)

y = [binomial_dist(a, 50, i) for i in x]

plt.bar(x, y, align="center", width=0.4, color="blue", 
             alpha=0.5, label="binomial p= " + "{:.1f}".format(a))

plt.legend()
plt.ylim(0, 0.3)
plt.xlim(0, 50)

plt.show()
plt.savefig('binomial_dist_sample.png')

成功確率$10\%$なのでやはり$4,5$回成功する確率が最も高いことがわかります。期待値が$np=50×0.1=5$であることとも合致しています。また、$10$回以上成功する確率は非常に低く、$20$回となると奇跡のレベルであることもわかります。

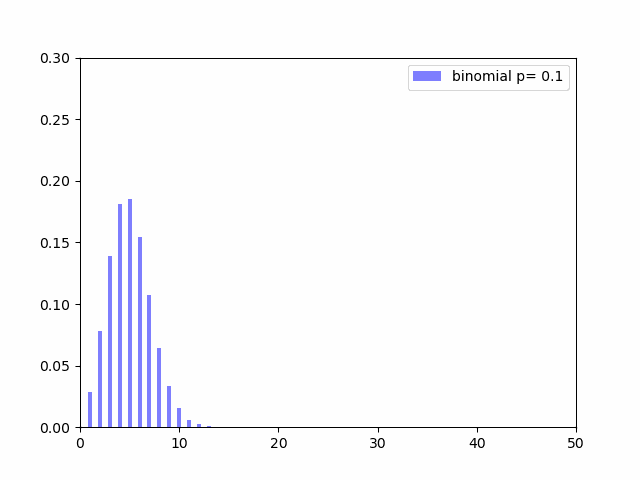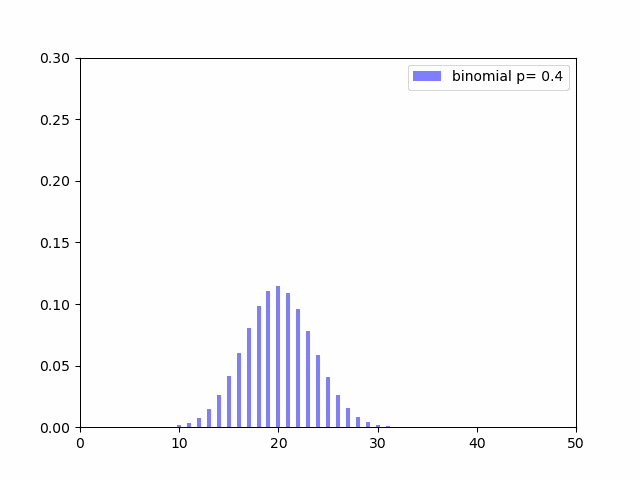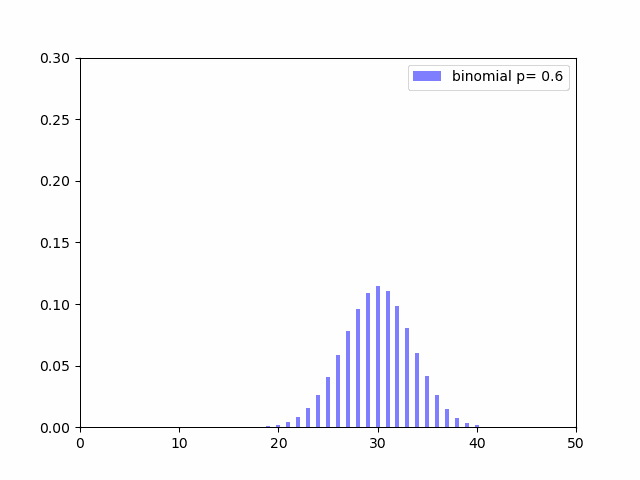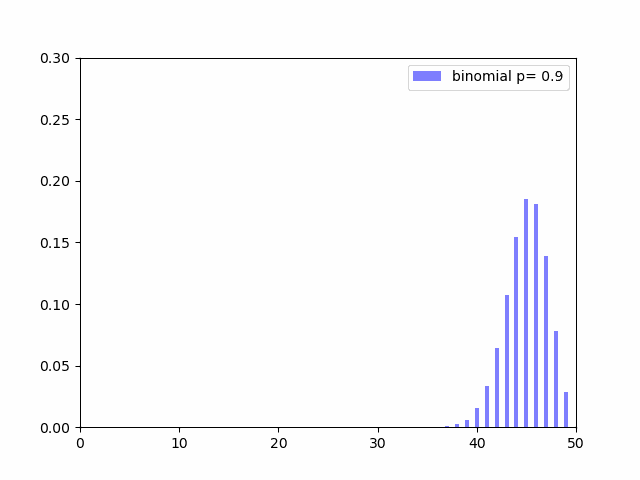
では成功確率を上げていく($p$を変化させる)と分布がどういう変化していくかを見てみます。

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
%matplotlib notebook

def comb_(n, k):
    result = math.factorial(n) / (np.math.factorial(n - k) * np.math.factorial(k))
    return result


def binomial_dist(p, n, k):
    result = comb_(n, k) * (p**k) * ((1 - p) ** (n - k))
    return result

fig = plt.figure()

def update(a):
    plt.cla() 
    x =  np.arange(1, 50, 1)
    y = [binomial_dist(a, 50, i) for i in x]

    plt.bar(x, y, align="center", width=0.4, color="blue", 
                 alpha=0.5, label="binomial p= " + "{:.1f}".format(a))

    plt.legend()
    plt.ylim(0, 0.3)
    plt.xlim(0, 50)


ani = animation.FuncAnimation(fig,
                              update,
                              interval=1000,
                              frames = np.arange(0.1, 1, 0.1),
                              blit=True)
plt.show()
ani.save('Binomial_dist.gif', writer='pillow') 

$p$が$0.5$(成功確率が$50\%$)に近いほど分布の裾が広くなり、$0$や$1$に近いほど尖った形になっているのがわかると思います。$V(X) = np(1 - p)$の式を見ても$p$が$0.5$に近いほど分散の値が大きくなることがわかります。成功確率がイーブンだとその分結果がばらつくのも何となくの感覚と一致しています。

ポアソン分布

続いてはポアソン分布です。
単位時間当たりに平均$\lambda$回起こる事象が丁度$k$回起こる確率を表す確率分布をポアソン分布と呼びます。

• 1時間に特定の交差点を通過する車両の台数
• 1時間にwebサイトにアクセスされるアクセス数
• 1日に受け取る電子メールの件数
• ある一定の時間内の店への来客数

などがポアソン分布に従うとされています。

ポアソン分布確率質量関数の数式は下記のように表されます。

P(X=k) = \frac{\lambda^k \mathrm{e}^{-\lambda}}{k!}

非常にわかりにくい式ですが詳しい導出過程が知りたい方は以前の記事をご覧ください。
また確率変数$X$がポアソン分布に従う時の期待値$E(X)$と分散$V(X)$は以下のようになります。

E(X) = \lambda

V(X) = \lambda

平均$\lambda$回起こる事象の話をしているので、期待値がそのまま$\lambda$であるのは納得感があります。

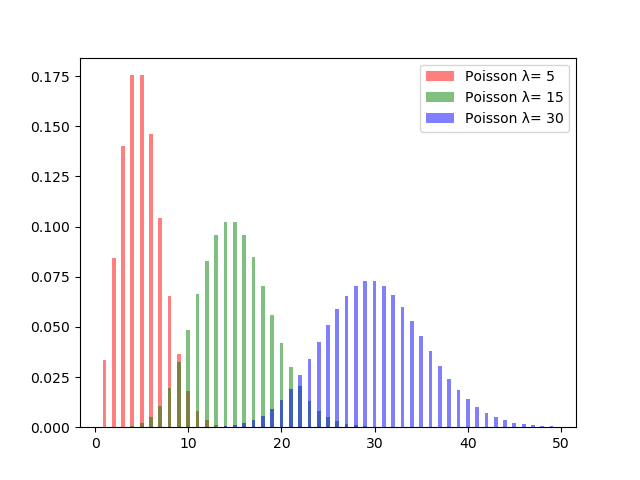
ではPythonで確率分布を描画してみます。単位時間あたり平均$5$回発生する事象、平均$10$回発生する事象、平均$15$回発生する事象、それぞれがどのような形になるかポアソン分布を重ねて描画してみます。

import numpy as np
import matplotlib.pyplot as plt

def poisson(k, lambda_):
    k = int(k)
    result = (lambda_**k) * (np.exp(-lambda_))  / np.math.factorial(k)
    return result

x =  np.arange(1, 50, 1)
y1= [poisson(i, 5) for i in x]
y2= [poisson(i, 15) for i in x]
y3= [poisson(i, 30) for i in x]

plt.bar(x, y1, align="center", width=0.4, color="red"
                ,alpha=0.5, label="Poisson λ= %d" % 5)

plt.bar(x, y2, align="center", width=0.4, color="green"
                ,alpha=0.5, label="Poisson λ= %d" % 15)

plt.bar(x, y3, align="center", width=0.4, color="blue"
                ,alpha=0.5, label="Poisson λ= %d" % 30)

plt.legend()
plt.savefig('Poisson_sample.png')
plt.show()

$\lambda$の値がイコールで分散にもなっているため、$\lambda$の値が大きくなればなるほど確率分布の裾が広がっていきます。$\lambda$を大きくして行った時の分布の変化の動きを見るとこのようになります。

import matplotlib.pyplot as plt
import matplotlib.animation as animation
import numpy as np
from scipy.stats import poisson
fig = plt.figure()

def update(a):
    plt.cla()

    x =  np.arange(1, 50, 1)

    y = [poisson.pmf(i,a) for i in x]

    plt.bar(x, y, align="center", width=0.4, color="red", 
                 alpha=0.5, label="Poisson λ= %d" % a)

    plt.legend()
    plt.ylim(0, 0.3)
    plt.xlim(0, 50)

ani = animation.FuncAnimation(fig,
                              update,
                              interval=500,
                              frames = np.arange(1, 31, 1),
                              blit=True)
plt.show()
ani.save('Poisson_distribution.gif', writer='pillow') 

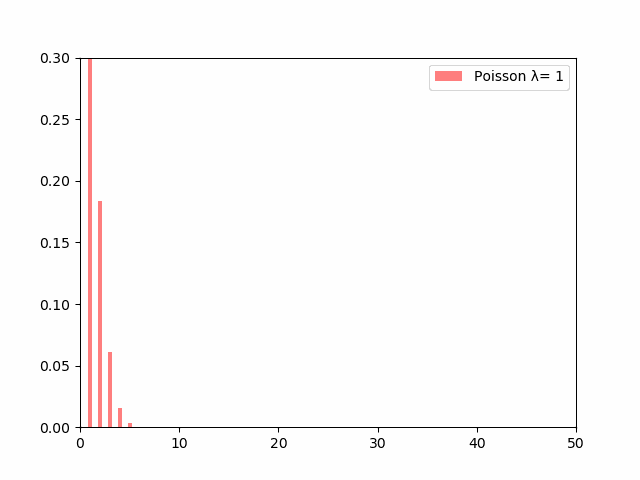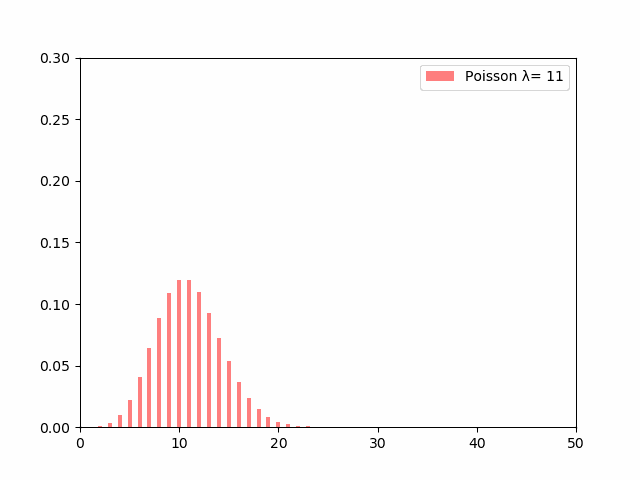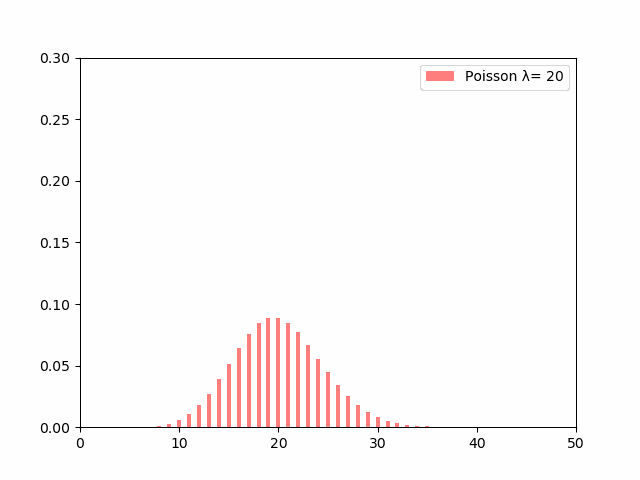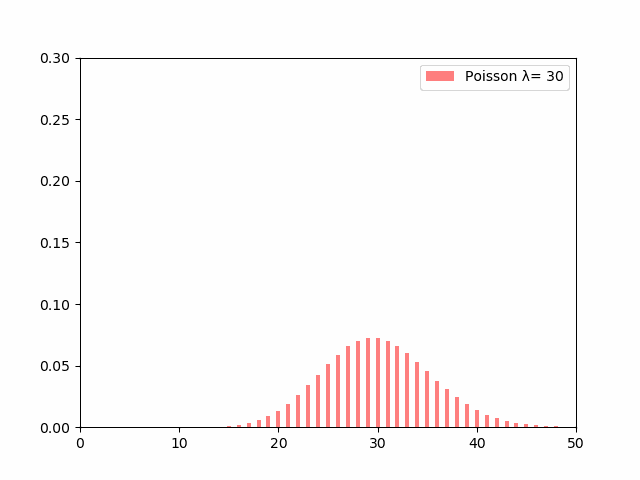
$\lambda$の値が大きくなるにつれて分布の裾が広がるように変化していっているのがわかります。
単位時間あたりの事象の平均発生回数である$\lambda$が大きければ大きいほど、その事象が発生する回数はバラついていくということになります。

二項分布とポアソン分布

ポアソン分布は実は二項分布を元に作成された確率分布です。$np = \lambda$を一定に保ちながら$n→∞$に$p→0$に近づけたのがポアソン分布です。(ポアソン極限定理と呼ばれているものです。以前の記事で解説しているので興味のある方はそちらをご覧ください。)

つまり二項分布に従う事象の中でも数が多くて滅多に起きない事象がポアソン分布に従うということです。

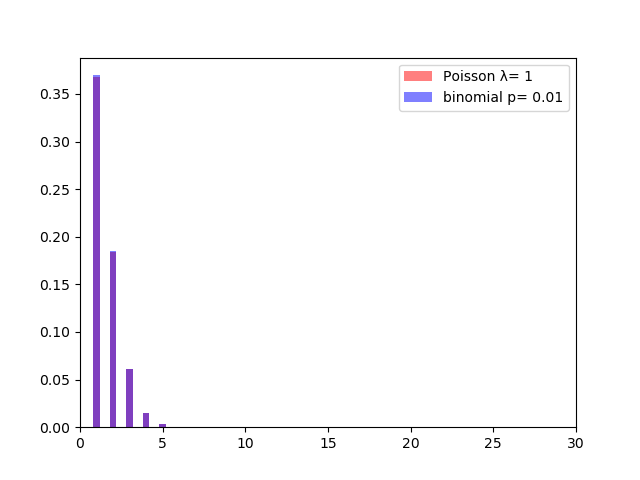
具体例として$n=100$ $p = 0.1$の二項分布と$\lambda = 1$のポアソン分布を重ねて描画してみます。

import numpy as np
import matplotlib.pyplot as plt

def poisson(k, lambda_):
    result = (lambda_**k) * (np.exp(-lambda_))  / np.math.factorial(k)
    return result

def comb_(n, k):
    result = math.factorial(n) / (np.math.factorial(n - k) * np.math.factorial(k))
    return result

def binomial_dist(p, n, k):
    result = comb_(n, k) * (p**k) * ((1 - p) ** (n - k))
    return result

x =  np.arange(1, 100, 1)
y1= [poisson(i, 1) for i in x]
y2 = [binomial_dist(0.01, 100, i) for i in x]

plt.xlim(0, 30)

plt.bar(x, y1, align="center", width=0.4, color="red"
                ,alpha=0.5, label="Poisson λ= %d" % 1)

plt.bar(x, y2, align="center", width=0.4, color="blue", 
                 alpha=0.5, label="binomial p= " + "{:.2f}".format(0.01))

plt.legend()
plt.savefig('bino_poisson.png')
plt.show()

分布が殆どピッタリ重なっていることがわかります。
このように分布を実際の描画することで分布間の関係性の理解も容易になります。

NEXT

次回は「幾何分布」「指数分布」「負の二項分布」を取り上げます。