はじめに
統計を勉強していると必ず出てくるポアソン分布ですが、例の確率分布の式が中々頭に入ってこなかったので確率分布の導出から丁寧に追って理解しようと考えました。イメージを掴むためにPythonで描画も行います。
参考
ポアソン分布の理解とその分布の描画を行うに当たって下記を参考にさせていただきました。
- 【大学数学】ポアソン分布(具体例やその意味、ポアソンの極限定理)【確率統計】
- 統計学入門 (基礎統計学Ⅰ)
- ポアソン分布とは何か。その性質と使い方を例題から解説 【馬に蹴られて死ぬ兵士の数を予測した数式】
- ポアソン分布の期待値・分散の導出(証明)
ポアソン分布の理解
ポアソン分布とは何か
P(X=k) = \frac{\lambda^k \mathrm{e}^{-\lambda}}{k!}
ポアソン分布とは単位時間当たりに平均$\lambda$回起こる事象が丁度$k$回起こる確率を表す確率分布です。ポアソン分布は上記の確率分布に従うとされていますが、式内でネイピア数の累乗が出て来たり、階乗が出て来たりで良く分かりません。何ぜこのような式になるのかを含めて以下で追って行こうと思います。
また、確率変数$X$がパラメータ$\lambda$のポアソン分布に従う時、$X〜Po(\lambda)$と表記されてります。
ポアソン分布に従う事象の例としては下記のようなものがあるとされています。
- 1時間に特定の交差点を通過する車両の台数
- 1時間にwebサイトにアクセスされるアクセス数
- 1日に受け取る電子メールの件数
- ある一定の時間内の店への来客数
また歴史的には**「プロイセン陸軍で馬に蹴られて死亡した兵士数」**が最初のポアソン分布の当てはめ例とされているらしく、$1$年間を単位時間として$\lambda = 0.61$のポアソン分布に従うということが示されています。
具体的に1つ確率を計算してみます。
ex)1時間に平均5回アクセスされるサイトが10回アクセスさせる確率($X〜Po(5)$:ポアソン分布に従う)
P(X=10) = \frac{5^{10} \mathrm{e}^{-5}}{10!} \fallingdotseq 0.018
とこのような感じで確率を導き出すことができます。この例の場合だと確率は$1.8%$と非常に小さいことがわかります。
ポアソン分布の導出(ポアソン極限定理)
ポアソン極限定理の概要
\lim_{\lambda = np, n\to \infty} {}_n \mathrm{C} _kp^{k}(1-p)^{n-k} = \frac{\lambda^k \mathrm{e}^{-\lambda}}{k!}
ポアソン分布はパラメータが$n$と$p=\lambda/n$である二項分布において、$\lambda$の値は一定としながら$n$を無限大に近づけることで、近似的に導出することが可能です。つまりポアソン分布は二項分布の極限であるということです。これをポアソンの極限定理と言います。
$\lambda$の値は一定としながら$n$を無限大に近づけるという操作を行うと、それに従って$p$の値は非常に小さくなります。非常に小さな発生確率にものに適用できる分布ということがわかるかと思います。
ポアソン極限定理の式展開
ポアソン極限定理がどのような式展開をしているか追っていきます。
{\begin{eqnarray}
\lim_{n\to \infty} {}_n \mathrm{C} _kp^{k}(1-p)^{n-k}
&=& \lim_{n\to \infty}\frac{n!}{(n-k)!k!}p^{k}(1-p)^{n-k} \\
&=&\lim_{n\to \infty}\frac{n(n-1)\cdots(n-k+1)}{k!}(\frac{\lambda}{n})^{k}(1-\frac{\lambda}{n})^{n-k} \\
&=&\lim_{n\to \infty}\frac{n}{n}\frac{n-1}{n}\cdots\frac{n-k+1}{n}(\frac{\lambda^{k}}{k!})(1-\frac{\lambda}{n})^{n}(1-\frac{\lambda}{n})^{-k} \\
&=&\frac{\lambda^{k}}{k!}\lim_{n\to \infty}(1-\frac{\lambda}{n})^{n} \\
&=&\frac{\lambda^{k}\mathrm{e}^{-\lambda}}{k!}
\end{eqnarray}
}
このような式展開でポアソン分布の確率分布を導き出しているのですが、わかりにくい式展開があるので一部下記で補足をします。
まず3行目から4行目の展開のところです。
$\frac{n}{n}\frac{n-1}{n}\cdots\frac{n-k+1}{n}$は$n$を無限大に近づけることで、全て値は$1$として処理できます。
また、$(1-\frac{\lambda}{n})^{-k}$も$n$を無限大に近づけることで$()$の中身が限りなく$1$に近づき、こちらも値は$1$として処理できます。
4行目から5行目の展開はネイピア数の下記定義式を利用しています。
\mathrm{e} = \lim_{x\to \infty}(1+\frac{1}{x})^{\frac{1}{x}}
上記にあてはめるように展開していくと下記のようになります。
{\begin{eqnarray}
\lim_{n\to \infty}(1-\frac{\lambda}{n})^{n} &=& \lim_{n\to \infty}(1-\frac{\lambda}{n})^{-\frac{1}{\frac{\lambda}{n}} (-\lambda)} \\
&=& \mathrm{e}^{-\lambda}
\end{eqnarray}}
これでポアソン分布の導出をすることができました。
ポアソン分布の性質
E(X) = \lambda \\
V(X) = \lambda
ポアソン分布の期待値・分散は共に$\lambda$であるという性質があります。
下記のそれぞれの導出過程を記載します。
ポアソン分布の期待値の導出過程
\begin{eqnarray*}E(X)&=&\sum_{k=0}^{n}kP(X=k)\\ &=&\sum_{k=0}^{n}k\frac{λ^{k}\mathrm{e}^{-\lambda}}{k!}\\ &=&\sum_{k=0}^{n}\frac{λ^{k}\mathrm{e}^{-\lambda}}{(k-1)!}\\ &=&λ\sum_{k=0}^{n}\frac{λ^{k-1}\mathrm{e}^{-λ}}{(k-1)!}\\ &=&λ\end{eqnarray*}
期待値と確率分布の性質からまず1行目の式をスタートさせます。
4行目から5行目の式展開は$\sum_{k=0}^{n}\frac{λ^{k-1}\mathrm{e}^{-λ}}{(k-1)!}$が結局はポアソン分布で取りうる全ての確率を足し合わせることになっているため値は$1$と置くことができ、このような式展開が可能になっています。
ポアソン分布の分散の導出過程
\begin{eqnarray*}V(X)&=&E(X^2)-{(E(X))}^2
\end{eqnarray*}
上記分散の性質から、$E(X^{2})$を導き出すことができれば分散も導き出すことができることがわかります。下記が$E(X^{2})$の導出過程になります。
\begin{eqnarray*}E(X^2)&=&\sum_{k=0}^{n}k^{2}P(X=k)\\ &=&\sum_{k=0}^{n}k^{2}\frac{λ^{k}\mathrm{e}^{-λ}}{k!}\\ &=&\sum_{k=0}^{n}(k(k-1)+k)\frac{λ^{k}\mathrm{e}^{-λ}}{k!}\\
&=&\sum_{k=0}^{n}k(k-1)\frac{λ^{k}\mathrm{e}^{-λ}}{k!}+\sum_{k=0}^{n}k\frac{λ^{k}\mathrm{e}^{-λ}}{k!}\\
&=&\sum_{k=0}^{n}\frac{λ^{k}\mathrm{e}^{-λ}}{(k-2)!}+λ\\ &=&λ^{2}\sum_{k=0}^{n}\frac{λ^{k-2}\mathrm{e}^{-λ}}{(k-2)!}+λ\\ &=&λ^{2}+λ
\end{eqnarray*}
上記を用いて分散を導出します。
\begin{eqnarray*}V(X)&=&E(X^2)-{(E(X))}^2 \\
&=& λ^{2} + λ - λ^{2} \\
&=& λ
\end{eqnarray*}
こちらでポアソン分布の期待値と分散を導出することができました。
ポアソン分布の描画
ポアソン分布をPythonで描画する
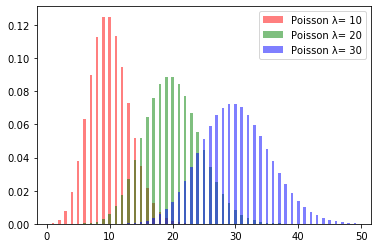
今回は単位時間あたり平均10回発生する事象、平均20回発生する事象、平均30回発生する事象のポアソン分布を重ねて描画してみます。
def poisson(lambda_, k):
k = int(k)
result = (lambda_**k) * (math.exp(-lambda_)) / math.factorial(k)
return result
x = np.arange(1, 50, 1)
y1= [poisson(10,i) for i in x]
y2= [poisson(20,i) for i in x]
y3= [poisson(30,i) for i in x]
plt.bar(x, y1, align="center", width=0.4, color="red"
,alpha=0.5, label="Poisson λ= %d" % 10)
plt.bar(x, y2, align="center", width=0.4, color="green"
,alpha=0.5, label="Poisson λ= %d" % 20)
plt.bar(x, y3, align="center", width=0.4, color="blue"
,alpha=0.5, label="Poisson λ= %d" % 30)
plt.legend()
plt.show()
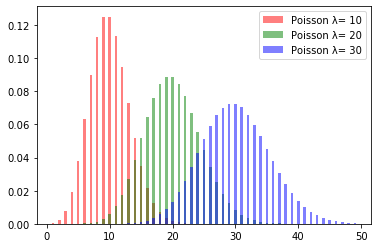
このような感じでグラフが描画できます。$λ$の値が大きくなればなるほど確率分布の裾が広がっていく様子が面白いですね。
ちなみにscipyというライブラリを用いると簡単にポアソン分布を描くことができます。
from scipy.stats import poisson
x = np.arange(1, 50, 1)
y1= [poisson.pmf(i, 10) for i in x]
y2= [poisson.pmf(i, 20) for i in x]
y3= [poisson.pmf(i, 30) for i in x]
plt.bar(x, y1, align="center", width=0.4, color="red"
,alpha=0.5, label="Poisson λ= %d" % 10)
plt.bar(x, y2, align="center", width=0.4, color="green"
,alpha=0.5, label="Poisson λ= %d" % 20)
plt.bar(x, y3, align="center", width=0.4, color="blue"
,alpha=0.5, label="Poisson λ= %d" % 30)
plt.legend()
plt.show()
Next
数式を丁寧に追って自分でPythonで描画すると、中々イメージの掴みにくかったポアソン分布を理解することができました。今後も統計関連で学んだことを色々まとめていこうと思います。