はじめに
重回帰分析の発展として正則化について勉強しました。
今回はリッジ回帰(L2正則化)についてまとめています。
参考
リッジ回帰(L2正則化)の理解に当たって下記を参考にさせていただきました。
- 機械学習のエッセンス 加藤公一(著) 出版社; SBクリエイティブ株式会社
- 正則化の種類と目的 L1正則化 L2正則化について
- リッジ回帰とラッソ回帰の理論と実装を初めから丁寧に
リッジ回帰(L2正則化)概要
重回帰分析の復習
リッジ回帰は重回帰分析を行う際の損失関数に対して正則化項を付与したものになります。
重回帰分析は下記のような損失関数を最小化する重みを見つけることで、最適な回帰式を導きだします。
$$L = \sum_{n=1}^{n} (y_{n} -\hat{y}_{n} )^2$$
- $y_{n}$は実測値
- $\hat{y}_{n}$の予測値
ベクトルの形式で表現するとこのような感じになります。
$$L = (\boldsymbol{y}-X\boldsymbol{w})^T(\boldsymbol{y}-X\boldsymbol{w})$$
- $\boldsymbol{y}$は目的変数の実測値をベクトル化したもの
- $\boldsymbol{w}$は重回帰式を作成した際の回帰係数をベクトル化したもの
- $X$はサンプル数$n$個、変数の数$m$個の説明変数の実測値を行列化したもの
上記$L$を最小化するような重み$\boldsymbol{w}$が求められればOKです。
上記$L$を$\boldsymbol{w}$で微分して$0$と置くと下記のようになります。
$$-2X^T\boldsymbol{y}+2\boldsymbol{w}X^TX = 0$$
こちらを解くことで重み$\boldsymbol{w}$を求めることができます。
リッジ回帰(L2正則化)
$$L = (\boldsymbol{y} - X\boldsymbol{w})^T (\boldsymbol{y} - X\boldsymbol{w}) + \lambda|| \boldsymbol{w} ||_{2}$$
上記がリッジ回帰(L2正則化)の損失関数の式になります。重回帰分析の損失関数に正則化項 $\lambda|| \boldsymbol{w} ||_{2} $を付け足した形になっています。
リッジ回帰(L2正則化)では上記のように重み$\boldsymbol{w}$のL2ノルムの2乗を加えることで正則化行います。
L2ノルムとは何か
ベクトル成分の差の2乗和の平方根(いわゆる"普通の距離"、ユークリッド距離と呼ばれる)がL2ノルムです。ノルムは「大きさ」を表す指標で他にL1ノルムやL∞ノルムなどが使われます。
L2正則化の効果
正則化項を損失関数に加えることで重み$\boldsymbol{w}$の値の大きさを抑える効果があります。
通常の重回帰分析の場合、最小化する項は下記のみです。
$$(\boldsymbol{y} - X\boldsymbol{w})^T (\boldsymbol{y} - X\boldsymbol{w})$$
こちらに正則化を加えると、下記項も含めて最小化を行う必要があります。
$$\lambda|| \boldsymbol{w} ||_{2}$$
重み$\boldsymbol{w}$が損失関数に与える影響が強くなるため、より重み$\boldsymbol{w}$の値の大きさを下げる方向に進んでいくことになります。また$\lambda$の大きさによってその度合いをコントロールしています。
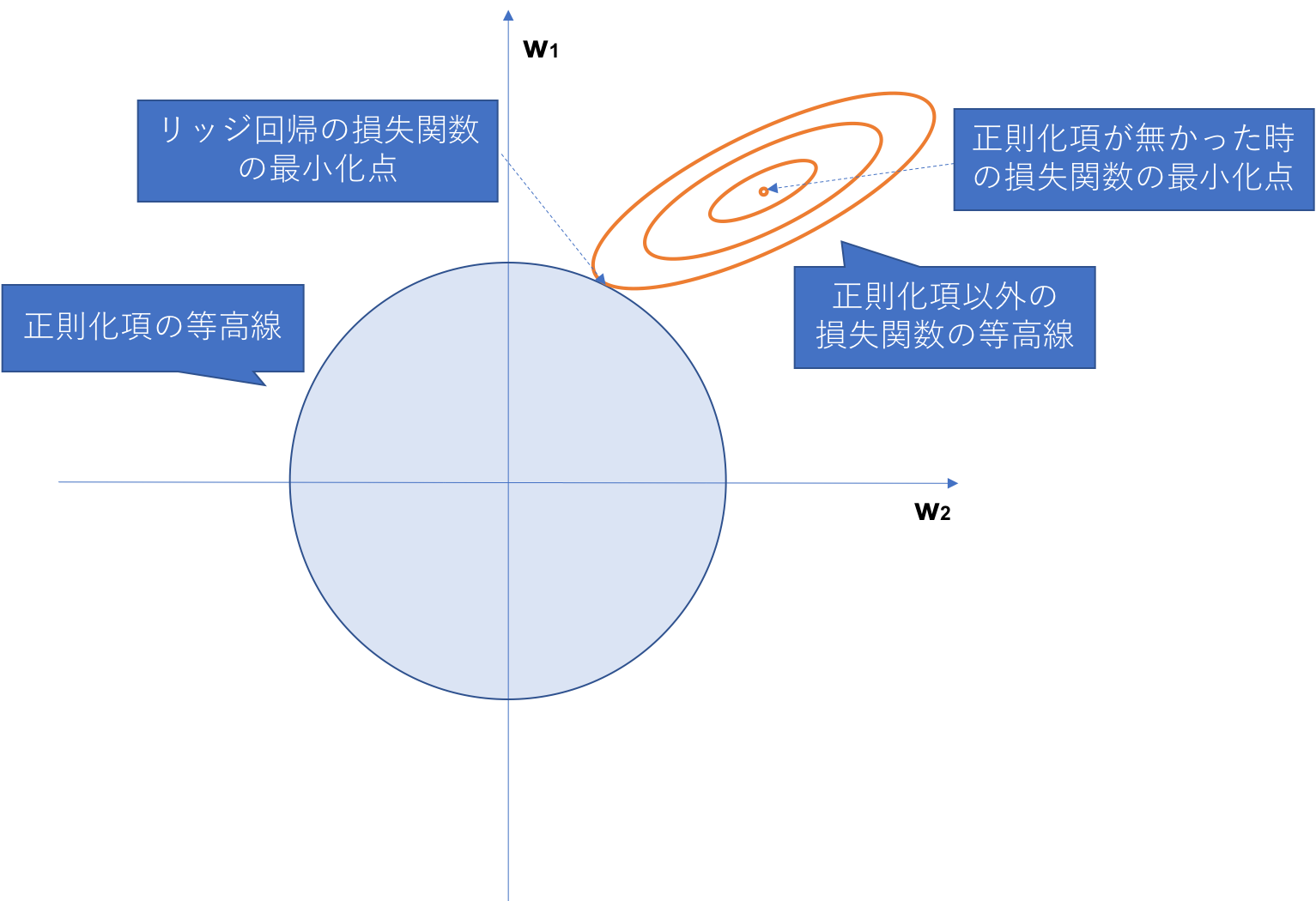
リッジ回帰(L2正則化)の説明として下記のような図がよく用いられます。
そのままだとわかりにくいため図の中で説明を加えています。下記は重みのパラメーターが2種類だった時の損失関数の値の等高線を2次元上にプロットしたものになります。正則化項を加えることで重みの値が下がっている様子が図上でわかるかと思います。
リッジ回帰(L2正則化)の重みの導出
$$L = (\boldsymbol{y} - X\boldsymbol{w})^T (\boldsymbol{y} - X\boldsymbol{w}) + \lambda|| \boldsymbol{w} ||_{2}$$
上記損失関数を重み$\boldsymbol{w}$で微分して$0$と置いて計算します。
-2X^T\boldsymbol{y}+2\boldsymbol{w}X^TX+2\lambda\boldsymbol{w} = 0 \\
(X^TX+\lambda I)\boldsymbol{w} - X^T\boldsymbol{y} = 0 \\
(X^TX+\lambda I)\boldsymbol{w} = X^T\boldsymbol{y} \\
\boldsymbol{w} = (X^TX+\lambda I)^{-1}X^T\boldsymbol{y}
こちらで重み$\boldsymbol{w}$を導き出すことができました。
リッジ回帰(L2正則化)を実装する
実装
下記がリッジ回帰(L2正則化)のモデルを自力実装した結果です。
import numpy as np
class RidgeReg:
def __init__(self, lambda_ = 1.0):
self.lambda_ = lambda_
self.coef_ = None
self.intercept_ = None
def fit(self, X, y):
#切片の計算を含めるために、説明変数の行列の1行目に全て値が1の列を追加
X = np.insert(X, 0, 1, axis=1)
#単位行列を作成
i = np.eye(X.shape[1])
#重みを求める計算式
temp = np.linalg.inv(X.T @ X + self.lambda_ * i) @ X.T @ y
#これは回帰係数の値
self.coef_ = temp[1:]
#これは切片の値
self.intercept_ = temp[0]
def predict(self, X):
#リッジ回帰モデルによる予測値を返す
return (X @ self.coef_ + self.intercept_)
検証
上記の自力実装のモデルと、sklearnの結果が一致しているか検証します。
今回はボストン住宅価格のデータセットを用いて検証を行います。データセットの中身については重回帰分析の検証をした記事の方に詳細を記載しております。
sklearnのモデル
from sklearn.datasets import load_boston
import pandas as pd
from sklearn.preprocessing import StandardScaler
# データの読み込み
boston = load_boston()
# 一旦、pandasのデータフレーム形式に変換
df = pd.DataFrame(boston.data, columns=boston.feature_names)
# 目的変数(予想したい値)を取得
target = boston.target
df['target'] = target
from sklearn.linear_model import Ridge
X = df[['INDUS', 'CRIM']].values
X = StandardScaler().fit_transform(X)
y = df['target'].values
clf = Ridge(alpha=1)
clf.fit(X, y)
print(clf.coef_)
print(clf.intercept_)
出力はこちら。上からモデルの回帰係数と切片です。
[-3.58037552 -2.1078602 ]
22.532806324110677
自力実装のモデル
X = df[['INDUS', 'CRIM']].values
X = StandardScaler().fit_transform(X)
y = df['target'].values
linear = RidgeReg(lambda_ = 1)
linear.fit(X,y)
print(linear.coef_)
print(linear.intercept_)
出力はこちら。上からモデルの回帰係数と切片です。
[-3.58037552 -2.1078602 ]
22.532806324110677
回帰係数の方は完全に一致したのですが、なぜか切片で微妙な差が出てしまいました。
調査したのですが原因がわからなかったため、このまま載せさせていただきます。
わかる方いらっしゃればご指摘ください...
Next
次はラッソ回帰(L1正則化)の理解と自力実装に挑戦します。