目的
C/GMRES法を実装すること
はじめに
本記事は、大塚先生の本(参考文献[1],[2],[4],[5]で公開いただいているサンプルコードとを基に構成しています。web上にC/GMRESに関する実装例があまり見つからなかったため、少しでも裾野を広げるために公開します。理解したとは言い難い状態で執筆しているため、誤りや怪しい点は随時指摘いただけると幸いです。
C/GMRESの制御フロー
各制御周期での処理フローは以下のようになる。
①制御量を出力する。
②GMRESで以下の式を解き、dUを求める。
\frac{\partial F}{\partial U}\dot{\;U} \left(t\right)=-\zeta F-\frac{\partial \;F}{\;\partial x}\dot{\;x\;} \left(t\right)-\frac{\partial \;F}{\partial t\;}
実際には、C/GMRESでは、式(8.42)を変形して、以下の式を解く
-\frac{\partial F\left(U,x+h\dot{x} ,t+h\right)}{\partial U}\dot{\;U} =-\zeta F\left(U,x,t\right)-\frac{F\left(U,x+h\dot{x} ,t+h\right)-F\left(U,x,t\right)}{h}
③U(n)=U(n-1)+ΔU×Δtで更新する(更新結果の出力は次回制御周期)
①GMRES法?
GMRES法は、反復解法の一種であり、Krylov部分空間法により、解を求める。ここで、行列Aは、非対称であるとする。
・そのままでは、数値計算精度の問題が出てくるため、Krylov部分空間の正規直交規定をArnoldi法で生成する。
・Krylov部分空間で表されるベクタの線形結合定数を残差ノルムを最小化することで決定し、近似解を求める。
その際の手段としてGivens回転を用いることもできる。
①-1.Arnoldi法?
正規直交基底を生成する方法の一種であり、クリロフ部分空間の基底ベクトルを求める際に利用。
①-2.Givens回転?
GMRES法内部では、上三角行列に近い行列$\bar{H_m }$を上三角行列に変換するために使用。
②ODE45によるMATLABでの非線形シミュレーション
制御対象が非線形なため、シミュレーションにも一工夫必要。
C/GMRES特有の実装はないので、好きな方法で実装して問題なし。
問題設定
本文書の制御対象は、以下のセミアクティブダンパ系([1]P23例2.1)である。
なお、$u_2$はダミー入力である。
\left\lbrace \begin{array}{l}
\dot{x} \left(t\right)=f\left(x\left(t\right),u\left(t\right)\right)\\
f\left(x\left(t\right),u\left(t\right)\right)=\left\lbrack \begin{array}{c}
x_2 \left(t\right)\\
ax_1 \left(t\right)+{\textrm{bx}}_2 \left(t\right)u_1 \left(t\right)
\end{array}\right\rbrack \\
C\left(u\left(t\right)\right)={\left(u_1 \left(t\right)-\frac{u_{\max } }{2}\right)}^2 +u_2 {\left(t\right)}^2 -\frac{u_{\max }^2 }{4}\\
C\left(u\left(t\right)\right)=0
\end{array}\right.
ただし、$a=-1,b=-1$
制約条件(上の2,3式目):$0\le ;u_1 \le u_{\max } =1$
サンプリング時間:1ms
初期値:${\left\lbrack x_1 ,x_2 \right\rbrack }^T ={\left\lbrack 2,0\right\rbrack }^T$
目標値:${\left\lbrack x_1 ,x_2 \right\rbrack }^T ={\left\lbrack 0,0\right\rbrack }^T$(=レギュレータ制御)
シミュレーション条件の設定
close all; clear all; format compact; beep off;%#ok<CLALL>
Ts = 1e-3; %サンプリング周期[sec]
t_sim_end = 20; %シミュレーション時間
tsim = 0:Ts:t_sim_end; %シミュレーションの基準となる時刻
% 操作入力列の初期化
% log.Uを入力値としてシミュレーションする(時刻はtsimが対応する)。
log.U = [];
% シミュレーション(ode45)の設定
opts = odeset('RelTol',1e-6,'AbsTol',1e-8);
シミュレーションの実装
CGMRESの制御器の設定
cgmres.ht = Ts; %前進差分近似の時間幅[sec]
cgmres.zeta = 1/cgmres.ht; %操作量の安定化ゲインζ
cgmres.tf = 1; %予測時間の最終長さ[sec]
cgmres.alpha = 0.5; %予測時間の上昇ゲイン
cgmres.N = 5; %予測区間の分割数
% 評価関数中の重み
cgmres.q = [1; 10]; %状態に対する重み
cgmres.s = [1; 10]; %終端状態に対する重み
cgmres.r = [0.01;0.01]; %操作量に対する重み
%入力上限(下限は0)
cgmres.umax = 1;
% 初期条件
% (u0の初期値はニュートン法などで与えること。適当な値では計算が収束しないことがある)
cgmres.x0 = [2;0]; %コントローラに与える初期状態(今回はプラントの初期状態も同値とした)
cgmres.u0 = [0.01;0.9;0.03]; %コントローラに与える初期操作量
% 制御上、多様する値を先に計算しておく(必要なところで都度計算でもよい)
cgmres.len_x = length(cgmres.x0); %状態の数
cgmres.len_u = length(cgmres.u0); %操作量の数
cgmres.len_lmd = cgmres.len_x; %随伴変数の数
入力の初期値を計算(Newton法)
[4]をそのまま引っ張ってきています(筆者の理解不足なため)。
cgmres.u0 = [1 2 3]';
lmd0 = dPhidx(cgmres.x0,cgmres.r);
for i = 1:20
cgmres.u0 = cgmres.u0 - CalcHHuu(cgmres.u0, cgmres.r)...
\ CalcHu(cgmres.x0,lmd0,cgmres.u0, cgmres.r) ;
end
% シミュレーション用に初期出力をコピーする
log.U = cgmres.u0;
制御ステップ毎に更新する、操作入力とその微分(N-1ステップ先まで)$U,\dot{U}$と
N-1ステップ先までの状態および随伴変数の予測値を初期化する。
U\left(t\right)=\left\lbrack \begin{array}{c}
{\mathit{\mathbf{u}}}_0^* \left(t\right)\\
\rho_0^* \left(t\right)\\
\vdots \;\\
{\mathit{\mathbf{u}}}_{N-1}^* \left(t\right)\\
\rho_{N-1}^* \left(t\right)
\end{array}\right\rbrack =\left\lbrack \begin{array}{c}
\left\lbrack \begin{array}{c}
u_0^* \left(t\right)\\
v_0^* \left(t\right)\\
\rho_0^* \left(t\right)
\end{array}\right\rbrack \\
\vdots \;\\
\left\lbrack \begin{array}{c}
u_{N-1}^* \left(t\right)\\
v_{N-1}^* \left(t\right)\\
\rho_{N-1}^* \left(t\right)
\end{array}\right\rbrack
\end{array}\right\rbrack \in R^{3N\times 1}
\textrm{cgmres}\ldotp U={\left\lbrack \begin{array}{ccccccc}
u_1 \left(0\right) & u_2 \left(0\right) & \rho \left(0\right) & \cdots & u_1 \left(N-1\right) & u_2 \left(N-1\right) & \rho \left(N-1\right)
\end{array}\right\rbrack }^T
\textrm{cgmres}\ldotp X=\left\lbrack \begin{array}{ccc}
x_1 \left(0\right) & \cdots & x_1 \left(N-1\right)\\
x_2 \left(0\right) & \cdots & x_2 \left(N-1\right)
\end{array}\right\rbrack ,\textrm{cgmres}\ldotp \textrm{Lambda}=\left\lbrack \begin{array}{ccc}
\lambda_1 \left(1\right) & \cdots & \lambda_1 \left(N\right)\\
\lambda_2 \left(1\right) & \cdots & \lambda_2 \left(N\right)
\end{array}\right\rbrack
cgmres.U = zeros(cgmres.len_u*cgmres.N,1);
cgmres.U = repmat(cgmres.u0, cgmres.N,1);
cgmres.dU = zeros(cgmres.len_u*cgmres.N,1);
cgmres.X = zeros(cgmres.len_x,cgmres.N);
cgmres.Lambda = zeros(cgmres.len_lmd,cgmres.N);
シミュレーションループ
log.X(:,1) = cgmres.x0; %シミュレーション結果の記録(ただしシミュレーションステップ毎に利用するので更新忘れないこと)
for i=1:length(tsim)
$u\left(t\right)=u_0^* \left(t\right)$をシステムへの制御入力とする。
%ステップi-1でのcgmresで計算した操作量をステップiで出力する
log.U(:,i) = cgmres.U(1:3);
%ステップiまでのシミュレーション計算
% 1ステップ前の状態量を初期値として、前回ステップと今回ステップの操作量を基にシミュレーションした
if i ~= 1
[t,xi] = ode45( @(t,xi) NLTI_Plant(t,xi,tsim(i-1:i),log.U(1,i-1:i)) ,...
[tsim(i-1) tsim(i)] , log.X(:,i-1) , opts);
else
xi = cgmres.x0';
end
ステップiにおける状態量$x$とその微分$\dot{x}$(GMRESで行列F計算する際に使用)
current.x = xi(end,:)';
log.X(:,i) = current.x;
予測時間長さをだんだんと伸ばす
予測ステップ数はN固定で、予測時間長さがだんだんと伸びていくイメージ
%予測時間を可変にする
cgmres.t_cur = cgmres.tf * (1-exp(-cgmres.alpha * (i-1)*Ts));
log.T(i) = cgmres.t_cur; %予測時間長さのログ
GMRES法
連立一次方程式(1.33)を$\dot{U} \left(t\right)$について解く。
式(1.33) $\frac{\partial F}{\partial U}\dot{\;U} \left(t\right)=-\zeta F-\frac{\partial \;F}{\;\partial x}\dot{\;x\;} \left(t\right)-\frac{\partial \;F}{\partial t\;}$
⇒$-\frac{\partial F\left(U,x+h\dot{x} ,t+h\right)}{\partial U}\dot{;U} =-\zeta F\left(U,x,t\right)-\frac{F\left(U,x+h\dot{x} ,t+h\right)-F\left(U,x,t\right)}{h}$
\item{ 右辺は各制御ステップで容易に計算可能な定数である。よって、右辺をb、x=$\dot{;U}$,$A=-\frac{\partial F\left(U,x+h\dot{x} ,t+h\right)}{\partial U}$として、$\textrm{Ax}=b$の連立方程式とみなせる。 }
\item{ この連立方程式をGMRES法で解くが、GMRES法(前回記事および参考文献[x]参照)のArnoldi法L3におけるAと基底ベクトルとの積${\textrm{Av}}_j$の計算のためには、行列Fの行列Uによる微分が必要である。←面倒。 }
\item{ ここで、Arnoldi法に必要な左辺の、$\frac{\partial F\left(U,x+h\dot{x} ,t+h\right)}{\partial U}v_j$の計算を見てみると($x=\dot{U}$なので$\dot{U} =v_j$で${\textrm{Av}}_j$が計算できることになる)が、これ(ヤコビ行列とベクトルの積)は方向微分であるので、十分に小さい正の実数hを用いて、最終的に以下で${\textrm{Av}}_j$の計算を代用できる([1]P17最下部)。 }
{\textrm{Av}}_j =\frac{\partial F\left(U,x+h\dot{x} ,t+h\right)}{\partial U}v_j =\frac{F\left(U+{\textrm{hv}}_j ,x,t\right)-F\left(U,x,t\right)}{h}\cdots \left(1\right)
定数項bおよび1つ目の規定ベクトルの計算
\hfill \break
current.dx = Func(current.x, cgmres.U(1));
%関数Fの状態微分
Fxt = CalcF(cgmres.U,current.x + (current.dx * cgmres.ht) , cgmres);
%関数F
F = CalcF(cgmres.U, current.x, cgmres);
%右辺(既知項)を計算する
Right = -cgmres.zeta .* F - ((Fxt - F) ./ cgmres.ht);
%関数Fの入力、状態微分
Fuxt = CalcF(cgmres.U + (cgmres.dU * cgmres.ht), ...
current.x + (current.dx * cgmres.ht) ,cgmres);
Left = ( ( Fuxt - Fxt ) / cgmres.ht ); % 未知項を左辺にまとめる
k = cgmres.len_u * cgmres.N; % GMRESの最大繰り返し回数(離散時間2点境界値問題の要素数と等しい)
% 初期残差
r0 = Right - Left;
%1つ目の基底ベクトル
Vm(:,1) = r0 ./ norm(r0);
Arnoldi法
・Arnoldi法で基底ベクトルを1つずつ作成する
% Arnoldi process(Hm_を作成する)
Hm = zeros(3,3);
% GMRESの繰り返し回数(基底ベクトルの数)
m = cgmres.len_u * cgmres.N;
%Arnoldi法
for j=1:m
Fuxt = CalcF(cgmres.U + ( Vm(:,j) * cgmres.ht ) , ...
current.x + (current.dx * cgmres.ht),cgmres);
Av = ( ( Fuxt - Fxt ) / cgmres.ht ); %Fxtは関数Fの状態微分
%Line 3
for k=1:j
Hm(k,j)=Av'*Vm(:,k);
end
%Line 4
temp_vec = 0;
for k = 1:j
temp_vec = temp_vec + Hm(k,j).*Vm(:,k);
end
v_hat = Av - temp_vec;
%Line 5
Hm(j+1,j) = norm(v_hat);
Vm(:,j+1) = v_hat ./ Hm(j+1,j);
end
Givens回転
\hfill \break
[UTMat,Omega] = ToUTMat(Hm);
e = zeros( k + 1, 1 );
e(1) = 1;
gm_ = norm(r0)*e;
for k=1:length(Omega)
gm_ = Omega{k}*gm_;
end
掃き出し法
上三角行列になっているので、下から順番に確定していけばよい。
min_y = zeros(length(UTMat)-1,1); %解の保存先
for k=length(UTMat)-1 :-1:1
min_y(k) = (gm_(k) - UTMat(k,:) * min_y)/UTMat(k,k);
end
操作入力の更新
数値積分($U\left(t+\Delta ;t\right)\textrm{=U}\left(t\right)+\dot{;U} \left(t\right)\Delta ;t$)して$U\left(t+\Delta ;t\right)$を求める
du_new = cgmres.dU + Vm(:,1:m)*min_y;
cgmres.dU = du_new;
cgmres.U = cgmres.U + cgmres.dU .* cgmres.ht;
end
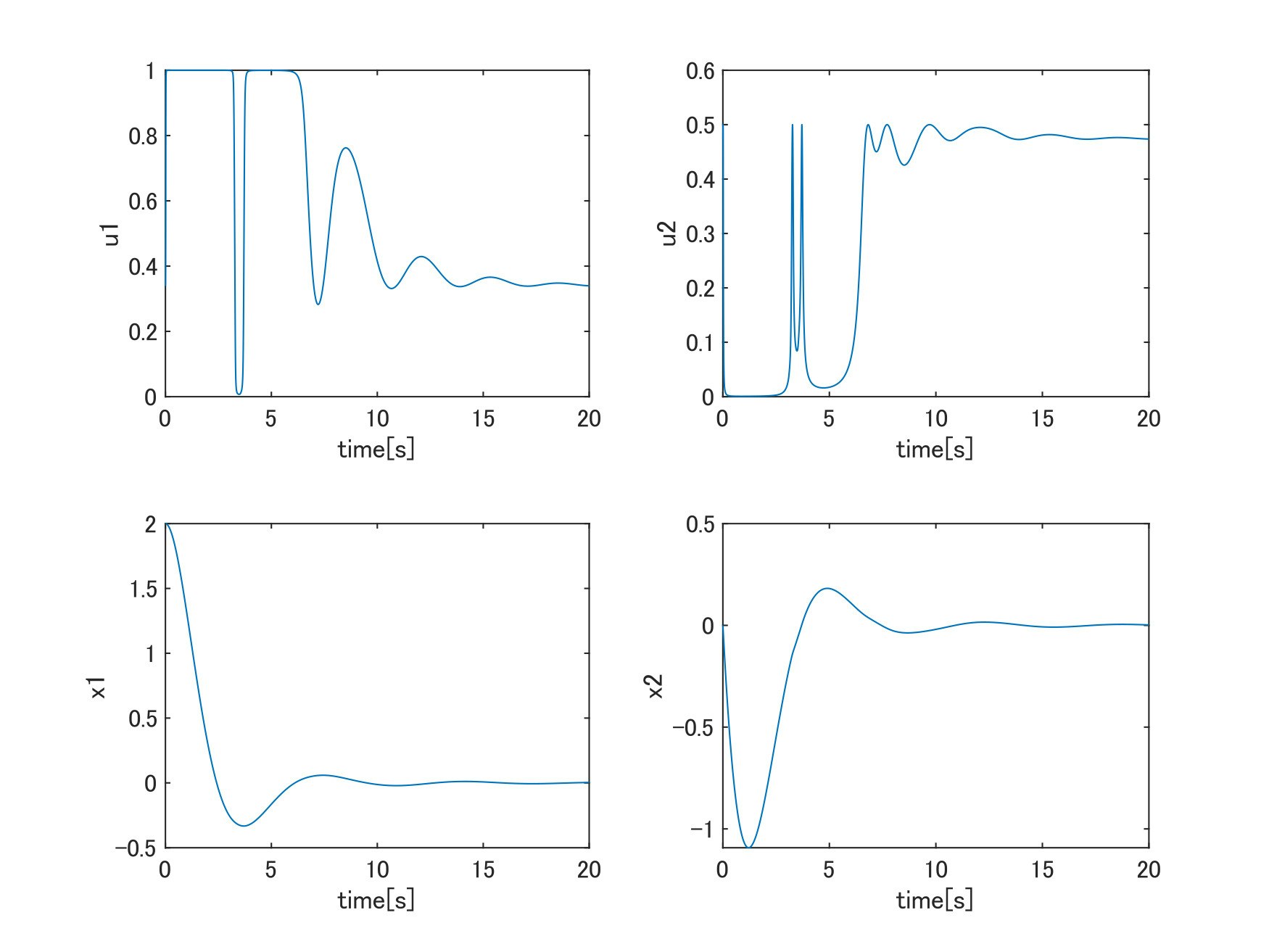
結果表示
figure();
subplot(2,2,1);
plot(tsim,log.U(1,:)); ylabel('u1'); xlabel('time[s]');
subplot(2,2,2);
plot(tsim,log.U(2,:)); ylabel('u2'); xlabel('time[s]');
subplot(2,2,3);
plot(tsim,log.X(1,:)); ylabel('x1'); xlabel('time[s]');
subplot(2,2,4);
plot(tsim,log.X(2,:)); ylabel('x2'); xlabel('time[s]');
おわりに
十分な精査もせず拙い内容ですが、各参考文献を読もうとしている方々のわずかばかりの助けにでもなればと思い公開いたします。必要なファイルは以下のgithubにup済みですので、そちらからダウンロードください。
https://github.com/j4312043/CGMRES_example_for_Qiita
ローカル関数
行列Fの計算
・この関数内でλとxの予測をしないといけない
(gmresの基底ベクトルがUに入ってくることになる)
\begin{array}{l}
F\left(U\left(t\right),x\left(t\right),t\right)=\left\lbrack \begin{array}{c}
{\left(\frac{\partial H}{\partial \mathit{\mathbf{u}}}\right)}^T \left(x_0^* \left(t\right),u_0^* \left(t\right),\lambda {\;}_1^* \left(t\right),t\right)\\
C\left({\mathit{\mathbf{x}}}_0^* \left(t\right),{\mathit{\mathbf{u}}}_0^* \right)\\
\vdots \;\\
{\left(\frac{\partial H}{\partial \mathit{\mathbf{u}}}\right)}^T \left(x_{N-1}^* \left(t\right),u_{N-1}^* \left(t\right),\lambda {\;}_N^* \left(t\right),t+T\right)\\
C\left({\mathit{\mathbf{x}}}_{N-1}^* \left(t\right),{\mathit{\mathbf{u}}}_{N-1}^* \right)
\end{array}\right\rbrack \in R^{3N\times 1} \\
=\left\lbrack \begin{array}{c}
r_1 u+\lambda_2 {\textrm{bx}}_2 +2\rho \left(u-0\ldotp 25\right)\\
-r_2 +2\rho_0^* v_0^* \\
{\left(u_0^* -0\ldotp 25\right)}^2 +{v_0^* }^2 -0\ldotp {25}^{2\;} \\
\vdots \;
\end{array}\right\rbrack
\end{array}
H=\frac{1}{2}\left(q_1 {x_1 }^2 +q_2 {x_2 }^2 +{r_1 u}^2 \right)-0\ldotp 01v+\lambda {\;}_1 x_2 +\lambda {\;}_2 \left(ax_1 +{\textrm{bx}}_2 u\right)+\rho \;\left({\left(u-0\ldotp 25\right)}^2 +v^2 -0\ldotp 0625\right)
\to {\left(\frac{\partial H}{\partial \mathit{\mathbf{u}}}\right)}^T =\left\lbrack \begin{array}{c}
r_1 u+\lambda_2 {\textrm{bx}}_2 +2\rho \left(u-0\ldotp 25\right)\\
-r_2 +2\rho v
\end{array}\right\rbrack
$C\left(\mathit{\mathbf{x}},\mathit{\mathbf{u}}\right)=u^2 +v^2 -{\left(\frac{0\ldotp 5}{2}\right)}^2$ 等式拘束条件
ここでのvの係数-0.01をcgmres.r(2)にサンプルではしている
function F = CalcF(U,x_current,cgmres)
%状態の予測計算
x = Forward(x_current,U,cgmres.N,cgmres.t_cur);
%随伴変数の計算
lmd = Backward(x,U, ...
cgmres.N,cgmres.t_cur,cgmres.s,cgmres.q);
%戻り値Fの初期化
F=zeros(cgmres.len_u*cgmres.N,1);
for i=1:cgmres.N
u = U(3*(i-1) + 1:3*(i-1) + 3); %引数の見通しを向上するため
F((1:3)+(3*(i-1))) = CalcHu(x(:,i),lmd(:,i),u,cgmres.r);
end
end
$\partial H/\partial u$(Hの入力微分)を計算する
function Hu = CalcHu(x,lmd,u,r)
Hu = [r(1)*u(1)+(-1)*lmd(2)*x(2)+2*u(3)*(u(1)-0.5)
2*u(3)*u(2)-r(2)
(u(1) - 0.5)^2 + u(2)^2 - 0.5^2];
end
状態xの予測計算
式(8.34)によって$x_0^* \left(t\right)$を決定し、式(8.33)をi=0からi=N-1まで計算し、状態の系列$x_i^* \left(t\right)\left(i=0,\cdots ,N\right)$を求める([2])。
式(8.34) $x_0^{*\;} \left(t\right)=x\left(t\right)$
式(8.33)$x_{i+1}^* \left(t\right)=x_{i\;}^* \left(t\right)+f\left(x_i^* \left(t\right),u_{i\;}^* \left(t\right),\right)\Delta \;\tau \;$
($\Delta \;\tau \;$=予測時間/N, Funcは状態量xの微分値)
%% 現在時刻からT秒未来までの状態の予測(Euler近似)
function X = Forward( x0, U, dv,TL )
temp.U = reshape(U,3,[])';
%式(8.33)
dt = TL / dv; %シミュレーションのステップ幅[sec]
len_x = length(x0);
X = zeros( len_x, dv ); %状態の数×ステップ数
X(:,1) = x0;
for cnt = 2 : dv
X(:,cnt) =X(:,cnt-1) + Func( X(:,cnt-1), temp.U( cnt-1 )) * dt;
end
end
状態方程式の計算
(再掲)$\dot{x} \left(t\right)=f\left(x\left(t\right),u\left(t\right)\right)=\left\lbrack \begin{array}{c}
x_2 \left(t\right)\
ax_1 \left(t\right)+{\textrm{bx}}_2 \left(t\right)u_1 \left(t\right)
\end{array}\right\rbrack$
% dx = f( x, u )
function dx = Func(x, u)
a = -1;
b = -1;
dx = [ ...
x(2); ...
a* x(1) + b * x(2) * u(1); ...
];
end
随伴変数λ系列の計算
TLは予測長さ
sf,qはそれぞれcgmres.s , cgmres.qが対応する(cgmres構造体を切り離したかった)
式(8.36)によって$\lambda_N^* \left(t\right)$を決定し、式(8.35)をi=N-1からi=1まで計算して随伴変数の系列$\lambda_{i;}^* \left(t\right)\left(i=1,\cdots ,N\right)$を求める([2]。
式(8.36) $\lambda_N^* \left(t\right)={\left(\frac{\partial \phi \;}{\partial \;x}\right)}^T \left(x_N^* \left(t\right),t+T\right)$
式(8.35) $\lambda {\;}_i^* \left(t\right)=\lambda {\;}_{i+1}^* \left(t\right)+{\left(\frac{\partial H}{\partial x}\right)}^T \left(x_i^* \left(t\right),u_i^* \left(t\right),\lambda {\;}_{i+1}^* \left(t\right),t+i\Delta \;\tau \;\right)\Delta \;\tau \;$
本シミュレーションでの$H,\phi ;$の設定を以下に示す
※t+Tの項は時不変の制御対象なので不要
\begin{array}{l}
\phi \left(x\right)=\frac{1}{2}\left(s_1 {x_1 }^2 +{s_2 x_2 }^2 \right)\\
\to \frac{\partial \phi \;}{\partial x}=\left\lbrack \begin{array}{c}
s_1 x_1 \\
{s_2 x}_2
\end{array}\right\rbrack
\end{array}
※$s_1 ,s_2$は終端状態の重み
\begin{array}{l}
H\left(x,u,\lambda \;\right)=\frac{1}{2}\left(q_1 {x_1 }^2 +q_2 {x_2 }^2 +{r_1 u}^2 \right)-0\ldotp 01v+\lambda {\;}_1 x_2 +\lambda {\;}_2 \left(ax_1 +{\textrm{bx}}_2 u\right)+\rho \;\left({\left(u-\frac{0\ldotp 5}{2}\right)}^2 +v^2 -\frac{0\ldotp 5^2 }{4}\right)\\
=\frac{1}{2}\left(q_1 {x_1 }^2 +q_2 {x_2 }^2 +{r_1 u}^2 \right)-0\ldotp 01v+\lambda {\;}_1 x_2 +\lambda {\;}_2 \left(ax_1 +{\textrm{bx}}_2 u\right)+\rho \;\left({\left(u-0\ldotp 25\right)}^2 +v^2 -0\ldotp 0625\right)\\
\to \frac{\partial H}{\partial x}=\left\lbrack \begin{array}{c}
q_1 x_1 +\lambda {\;}_2 a\\
q_2 x_2 +\lambda_1 +\lambda_2 \textrm{bu}
\end{array}\right\rbrack
\end{array}
%% 現在時刻からT秒未来までの随伴変数の予測(Euler近似)
% 引数UはN×1の配列とすること(u_1のみの配列であり、u_2,rhoを含まないこと)
function lmd = Backward( X, U, dv, TL,s,q)
% 随伴変数λの系列はi=1からNまでがcgmres.Lambda(1:N)に対応する
lmd(:,dv) = dPhidx(X(:,dv),s);
% lmd(:,dv) = X(:,dv) .* s;
lmd = CalcLmd(lmd(:,dv) , X, U, TL,dv,q);
end
λの系列を予測計算
0\textasciitilde{}TL秒までのλを計算する
function lmd = CalcLmd(lambda_last , X,U,TL, dv,q)
lmd = zeros(2,dv); %初期化
lmd(:,end) = lambda_last;
dt = TL / dv; %今回の予測計算のステップ幅[sec]
for i=dv-1:-1:1
lmd(:,i) = lmd(:,i+1) + CalcHx(X(:,i),lmd(:,i+1),U(i),q) * dt;
end
end
$\partial H/\partial x$を計算する
x={\left\lbrack x_1 \;,x_2 \right\rbrack }^T ,\textrm{lambda}={\left\lbrack \lambda {\;}_1 ,\lambda {\;}_2 \right\rbrack }^T
\frac{\partial H}{\partial x}=\left\lbrack \begin{array}{c}
q_1 x_1 +\lambda {\;}_2 a\\
q_2 x_2 +\lambda_1 +\lambda_2 {\textrm{bu}}_1
\end{array}\right\rbrack
function Hx = CalcHx(x,lmd,u,q)
sys.a = -1;
sys.b = -1;
Hx = [q(1)*x(1) + sys.a*lmd(2)
q(2)*x(2)+lmd(1)+lmd(2)*sys.b*u(1)];
end
$\partial^2 H/\partial^2 x$(Hの2階入力微分)を計算する
function Huu = CalcHHuu( u, r )
Huu = [ ...
r(1)+u(3)*2.0, 0, -1+u(1)*2.0;
0, u(3)*2.0, u(2)*2.0;
-1+u(1)*2.0, u(2)*2.0, 0;
];
end
\matlabheadingtwo{$d\phi /\textrm{dx}$(ヘッセ行列の状態微分)の計算}
function Phix = dPhidx( x, s )
Phix = [ x(1) * s(1);x(2) * s(2) ];
end
Givens回転の計算
function [UTMat,Omega] = ToUTMat(H)
%UNTITLED HをGivens回転でもって上三角行列に変換する
m = length(H)-1; %Givens回転する回数
for i=1:m
nu = sqrt(H(i,i)^2 + H(i+1,i)^2);
c_i = H(i,i)/nu;
s_i = H(i+1,i)/nu;
Omega{i} = diag(ones(m+1,1));
Omega{i}(i:i+1,i:i+1) = [c_i,s_i
-s_i,c_i];
H = Omega{i} * H;
end
UTMat = H;
end
参考文献
・1章でC/GMRESについて解説されている。
2章以降は、応用例などの紹介のため本書で実質的に読むべきは1章のみ
・大塚先生のプログラムもHPからダウンロード可能。
"rhfuncu.c"がC/GMRESの制御計算のところで
その他はシミュレーション用コードなどなので、今回はどうでもいい
[2]非線形最適制御入門
・第8章でモデル予測制御(C/GMRES)について解説している。
[3]倒立振子で学ぶ制御工学
・倒立振子への適用例とサンプルコードへのリンクがある
・MATLAB/Simulink動作するサンプルプログラムが記事付随のGitHubにある
[5]非線形モデル予測制御におけるCGMRES法をpythonで実装する @Qiita
・C/GMRESの解説が大塚先生の本よりもわかりやすいかも。
一部流儀違い?がある気がする。
・GMRES法についての解説がないため、本記事だけですべて理解するのは厳しい。
(GMRES法を知っている人なら問題ない)
・GMRES法はこれベースで実装した。
一つずつ数式を追えば意外と理解できる。