二輪台車シミュレーションをMATLABで実装するー制御モデルと解法ー

1.事のあらまし

MATLABはいいぞ。（ただし値段）　でおなじみMATLABですが、
マイクロマウスの大会出場者であれば無償で使えます。

このことを周囲の人に言って回っていたら、ついに１人がその気になって
10万円のキットを買ったので、これはサポートしてやらなければと思いシミュレーションのMATLAB実装を思いつきました。
(なお著者はマイクロマウス持ってないし触ったこともほぼない)

また最近、制御工学の偉人たちと会話したときに
「MATLABはやっぱりmファイルが一番。simulinkは便利だけどブラックボックス」と
強烈に言われたので、私も高みに至るべくmファイルのみでの実装にこだわりました。
なおツールボックスは使っておらず、MATLABのみで実行可能です。

全２~３回の連載予定で、現段階における完成図は下記です。←保留します

2.マイクロマウス＝２輪台車の状態方程式

三平先生の論文「非ホロノミック系のフィードバック制御」
より、下記式で与えられます。

\frac{d}{dt}

\Biggl(
\begin{matrix}
x \\
y \\
\theta
\end{matrix}
\Biggr)
=\Biggl(
\begin{matrix}
\cos\theta\\
\sin\theta\\
0
\end{matrix}
\Biggr)
u_1+

\Biggl(
\begin{matrix}
0 \\
0 \\
1
\end{matrix}
\Biggr)
u_2

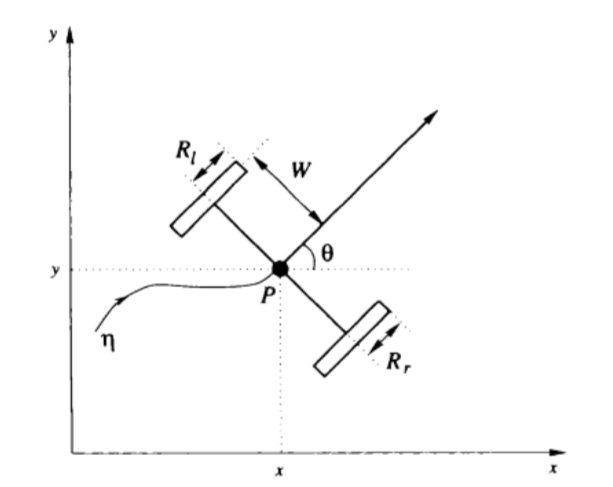
入力u1=速度v、入力u2=角速度ωであり、これらは本来であれば左右の車輪の回転速度によって決定されます。本ページでは説明の簡易化のため、u1,u2を任意に与えることが出来るものとします。

上式を一般化すると下記のように表すことが出来ます。

状態\:\xi = (\begin{matrix}
x&y&\theta
\end{matrix})^T\\
入力\:u=(\begin{matrix}
u_1&u_2\end{matrix})^T\\
\dot{\xi}=f(\xi)u

上式は非線形状態方程式の一種と言えます。
参考までに、線形な状態方程式は下記で与えられます。

\dot{x}=Ax+bu

極めて雑に言うのであれば、線形状態方程式のうちで行列A,Bが状態xの関数になっているものが非線形状態方程式と言えます。

制御になじみのない読者からすれば、線形が非線形になったからといって何が問題なの？
と思われるかも知れませんが、これが結構やっかいです。

3.非線形の何がやっかいか

制御モデルが非線形状態方程式で与えられる場合、線形状態フィードバックで安定化するには線形近似が必要となります。線形近似は「ある前提のもとに非線形を線形とみなす」考え方なので、前提が適用できない条件まで含めて安定化することは困難と言えます。(状態フィードバックについてはこちらを参照)

２輪台車のような『非ホロノミック拘束をもつ非線形システム』はさらにやっかいです。
詳しくは下記を参考下さい。
マイクロマウスと制御理論 (2)自由度と非ホロノミック拘束 | Tokoro's Tech-Note

いずれにしろ、非線形なシステムをPID制御のような通常のフィードバック制御で安定して制御することは難しく、時変の状態フィードバックや不連続フィードバックといった方法が必要となります。

「動かせるんだったらそれでいいじゃん」とも思われがちですが、一番の問題は通常の手法が使えないということは、通常の評価指標を使う事も出来ないということです。
動くようになったのはいいけど、それがＯＫなのかＮＧなのかを明確に(定量的に)判断するのが難しい、と言えばやっかいさが伝わるでしょうか。

制御にとって最も重要な要素の一つとしてフィードバック制御が挙げられますが、フィードバック制御は使い方によって毒にも薬にもなりえます。ですから、毒か薬かを判断できるか否かというのは非常に重要です。
（個人的には、制御工学＝制御『設計』工学であると思っている）

4.さておき、mファイル実装するには

二輪台車＝非線形状態方程式における時間応答を求めるには、何かしらのソルバを用いて収束演算を行う必要があります。ただしこれは厳密に解を求める場合であって、とりあえずの解が欲しい場合であれば、離散化した上で離散時間Δtを小さくすることでも似たような解は得られます。
なおソルバを使う場合も収束判定値を適宜設定しなければ適切な解が得られません。適切かどうかは使用者自身が判断しなければなりません。

融通が聞かんなぁと思われるかも知れませんが、それほどに非線形というものは扱いが難しいと理解下さい。なお線形状態方程式かつ入力も線形であればその解はラプラス変換および逆ラプラス変換を用いることで一意に求まります、線形スゲェ。

下記ではソルバとしてルンゲクッタを用いて解を導出するパターンと、離散化して導出するパターンの両方を示し、最後に結果比較を行います。

4.1 ルンゲクッタで解を導出する

MATLAB関数　ode45 ノンスティッフ微分方程式の求解を使います。
Dormand-Princean の陽的 Runge-Kutta (4,5) 公式に基づくそうです。
皆さん、意味が分かりますか？私は分かりません。

ちなみにode45関数なしで、ルンゲクッタ自体を自分で実装する方法もあります。
http://www.aoni.waseda.jp/yuuka/Sim/runge.pdf
皆さん、意味が分かりますか？私はちょっと無理そうです。

さておき。
状態方程式は

\dot{\xi}=f(\xi)u

であり、入力uは時間により変化させるものとします。
この場合、「時間依存の項をもつ ODE」を使うことになります。

前準備として、求解させる微分方程式をmファイルにて作成する必要があります。
冒頭の非線形状態方程式を参考に、TwoWheel.mとして下記作成します。

TwoWheel.m

function dxi = TwoWheel(t,xi,t1,u1,u2)
    u1 = interp1(t1,u1,t);
    u2 = interp1(t1,u2,t);
    dxi = zeros(3,1);%出力をベクトルとして定義
    dxi(1) = cos(xi(3)) * u1;
    dxi(2) = sin(xi(3)) * u1;
    dxi(3) = u2;
end

上記において、時間ベクトルtおよびそのときの状態xiはode45関数をコールした時に自動的に与えられます。
時間tが自動的に与えられるので、その時に応じた入力u1,u2が必要になりますが
tがどうなるか分からないので、ode45関数をコールする準備段階にて暫定的に時間t1ベクトルおよびそのときの入力u1,u2を定義しておき、ode45関数がコールされたら内挿(interp1)するようになっています。
なお４行目の

dxi = zeros(3,1);%出力をベクトルとして定義

を書いておかないと、出力が不定となるため呼び出したときにエラーとなります。
出力がベクトルの場合のサンプルがMathworks公式のヘルプに無く、ここで若干躓きました。
参考までにエラーコードは下記です。

@(T,XI)TWOWHEEL(T,XI,T1,U1,U2) は列ベクトルを返さなければなりません。
エラー: ode45 (line 115)
odearguments(FcnHandlesUsed, solver_name, ode, tspan, y0, options, varargin);

シミュレーションは上記ファイルに加えTwoWheelSim_R.mを作成することで行います。
（ファイル名は任意です）
本ファイルからTwoWheel.mを呼び出し、ode45関数にて求解します。
ode45関数の文法に@が入ってますが、無名関数みたいな使い方と理解しておくとよいでしょう。

TwoWheelSim_R.m

clear all;
close all;
opts = odeset('RelTol',1e-6,'AbsTol',1e-8);
dt = 0.05;%時間刻み
Tfin = 10;%シミュレーション終了時間
xi0 = zeros(3,1);%状態ξの初期値
t1 = [0:dt:Tfin];
u1 = ones(1,length(t1))*4;%速度
u2 = 0.1*t1;%角速度
[t,xi]= ode45(@(t,xi) TwoWheel(t,xi,t1,u1,u2),[0 Tfin],xi0,opts);
fig = figure(1);
plot(xi(:,1),xi(:,2))
hold on;
axis equal;
grid on;

入力は、とりあえず速度u1を一定値に、角速度u2をランプ増加としました。
他の入力がどうなるかは適宜試してみて下さい、
この場合の結果は下記です。

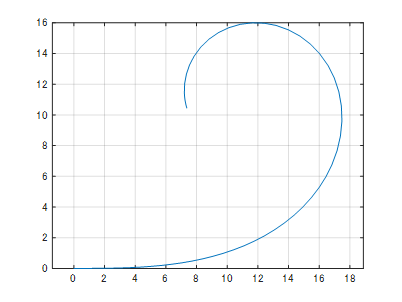
これだけだと何とも言えないので、離散化した場合との比較を行います。

4.2 状態方程式を離散化して解を導出する

丁寧すぎるとは思いますが、一応ラプラス変換→後退差分による離散化結果を下記示します。
（ちょっと自信ないです）Tsは離散時間です。

\Biggl(
\begin{matrix}
sX(s) \\
sY(s) \\
s\Theta(s)
\end{matrix}
\Biggr)
=\Biggl(
\begin{matrix}
\cos\Theta(s)\\
\sin\Theta(s)\\
0
\end{matrix}
\Biggr)
U_1(s)+

\Biggl(
\begin{matrix}
0 \\
0 \\
1
\end{matrix}
\Biggr)
U_2(s)
\\
\\
s=\frac{1-z^{-1}}{T_s}
\\
\\
\Biggl(
\begin{matrix}
x(n) \\
y(n) \\
\theta(n)
\end{matrix}
\Biggr)
=
\Biggl(
\begin{matrix}
x(n-1) \\
y(n-1) \\
\theta(n-1)
\end{matrix}
\Biggr)
+
\Biggl(
\begin{matrix}
\cos\theta(n)\\
\sin\theta(n)\\
0
\end{matrix}
\Biggr)
u_1(n)T_s+

\Biggl(
\begin{matrix}
0 \\
0 \\
1
\end{matrix}
\Biggr)
u_2(n)T_s

上記は厳密な結果ですが、右辺にθ(n)が含まれます。
２輪台車の場合、θ(n)がx(n),y(n)に依存しないのでθ(n)を先に求めておき、その上でx(n),y(n)の計算に利用することが可能です。下記では上式を離散化した場合の厳密式と定義することにします。

今回はそのケースではないですが、例えばθ(n)がx(n),y(n)に依存するような場合は、θ(n)を先に求めることが出来ません。この場合は右項のθ(n)の代わりにθ(n-1)を使うことで妥協します。
つまりはこう。

\Biggl(
\begin{matrix}
x(n) \\
y(n) \\
\theta(n)
\end{matrix}
\Biggr)
=
\Biggl(
\begin{matrix}
x(n-1) \\
y(n-1) \\
\theta(n-1)
\end{matrix}
\Biggr)
+
\Biggl(
\begin{matrix}
\cos\theta(n-1)\\
\sin\theta(n-1)\\
0
\end{matrix}
\Biggr)
u_1(n)T_s+

\Biggl(
\begin{matrix}
0 \\
0 \\
1
\end{matrix}
\Biggr)
u_2(n)T_s

下記では上式を離散化した場合の妥協案と定義することにします。

シミュレーションはTwoWheelSim_D.mを作成することで行います。
上記における厳密式と妥協案を平行評価します。
非線形状態方程式を書いたファイルであるTwoWheel.mは呼び出しません。

TwoWheelSim_D.m

clear all;
close all;
dt = 0.05;%%時間刻み=離散時間Tsとして使用
Tfin = 10;%シミュレーション終了時間
t1 = [0:dt:Tfin];
u1 = ones(1,length(t1))*4;
u2 = 0.1*t1;

xi_z = zeros(length(t1),3);
xi_z(1,:) = [0 0 0];%状態ξの初期値を設定
for i = 1:length(t1)-1
    %厳密式　θ(n),すなわち xi_z(i+1,3) をx(n),y(n)の計算に使う
    xi_z(i+1,3) = xi_z(i,3) + u2(i)*dt;
    xi_z(i+1,1) = xi_z(i,1) + u1(i)*cos(xi_z(i+1,3))*dt;
    xi_z(i+1,2) = xi_z(i,2) + u1(i)*sin(xi_z(i+1,3))*dt;
end
plot(xi_z(:,1),xi_z(:,2));
hold on;
axis equal;
grid on;

for i = 1:length(t1)-1
    %妥協案　θ(n-1),すなわち xi_z(i,3) をx(n),y(n)の計算に使う
    xi_z(i+1,1) = xi_z(i,1) + u1(i)*cos(xi_z(i,3))*dt;
    xi_z(i+1,2) = xi_z(i,2) + u1(i)*sin(xi_z(i,3))*dt;
    xi_z(i+1,3) = xi_z(i,3) + u2(i)*dt;
end
plot(xi_z(:,1),xi_z(:,2));

結果は下記です。厳密式と妥協案でそこそこの違いが出てしまいました。この差は離散時間Tsが大きいほど広がるものと予測されます。

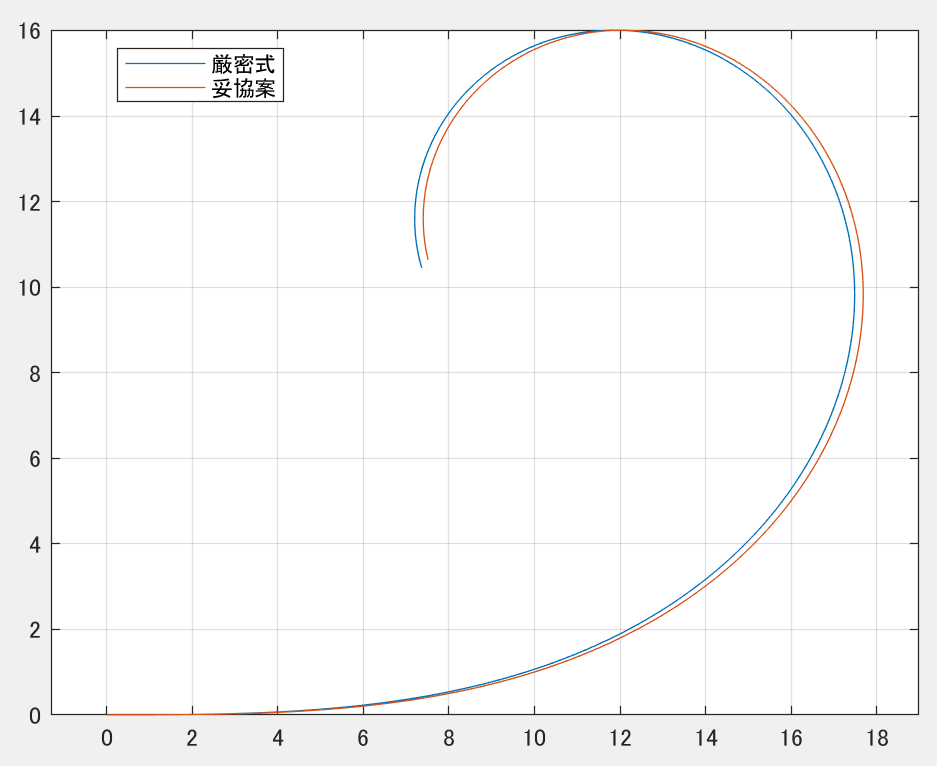
4.3ルンゲクッタによる求解と離散化による求解を比較する(妥協案ver)

さて、やっとこさ本題になります。
上記２つのmファイル(TwoWheelSim_R.m とTwoWheelSim_D.m)にて得られた結果を１つの図に示します。ここでは離散化による求解は妥協案のみ示すものとします。
妥協案というのはこれね。

\Biggl(
\begin{matrix}
x(n) \\
y(n) \\
\theta(n)
\end{matrix}
\Biggr)
=
\Biggl(
\begin{matrix}
x(n-1) \\
y(n-1) \\
\theta(n-1)
\end{matrix}
\Biggr)
+
\Biggl(
\begin{matrix}
\cos\theta(n-1)\\
\sin\theta(n-1)\\
0
\end{matrix}
\Biggr)
u_1(n)T_s+

\Biggl(
\begin{matrix}
0 \\
0 \\
1
\end{matrix}
\Biggr)
u_2(n)T_s

シミュレーション結果は下記。

時間刻みdt=0.1、すなわち離散時間=0.1の場合

時間刻みdt=0.05、すなわち離散時間=0.05の場合

時間刻みdt=0.01、すなわち離散時間=0.01の場合

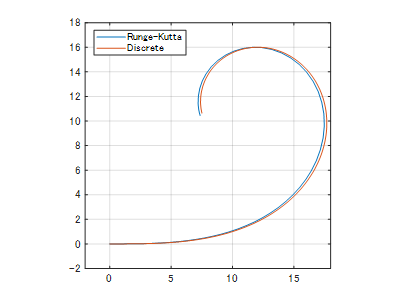
上記より、ルンゲクッタによる求解が正解であるという前提のもと、
見た目で判断するなら離散時間=0.01未満が適切　との結論が得られます。

なお、ルンゲクッタによる求解におけるサンプリング点はわずか77点です。
これに対し、離散時間=0.01のサンプリング点は1000点なので、データ量の圧縮という観点ではルンゲクッタが大幅に優れていることが伺えます。

4.4 ルンゲクッタによる求解と離散化による求解を比較する(厳密式ver)

上記はルンゲクッタと妥協案との比較を行いましたが、今度は厳密式との比較を行います。
厳密式というのはこれね。妥協案との差は右辺にθ(n)を使うことのみです。

\Biggl(
\begin{matrix}
x(n) \\
y(n) \\
\theta(n)
\end{matrix}
\Biggr)
=
\Biggl(
\begin{matrix}
x(n-1) \\
y(n-1) \\
\theta(n-1)
\end{matrix}
\Biggr)
+
\Biggl(
\begin{matrix}
\cos\theta(n)\\
\sin\theta(n)\\
0
\end{matrix}
\Biggr)
u_1(n)T_s+

\Biggl(
\begin{matrix}
0 \\
0 \\
1
\end{matrix}
\Biggr)
u_2(n)T_s

シミュレーション結果は下記。
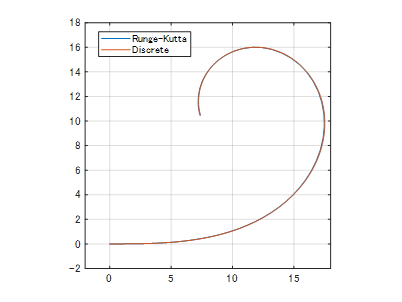
時間刻みdt=0.1、すなわち離散時間=0.1の場合

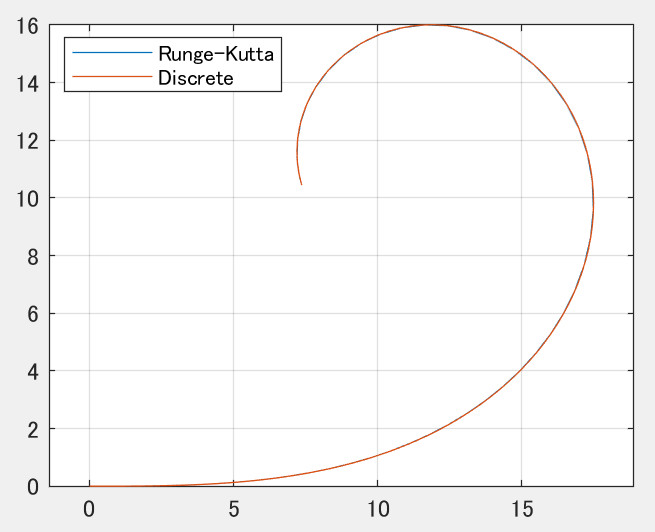
あれ、なんか結構いい感じになってしまった…！ サンプリング点は100点なので計算量も悪くないですね。

じゃあじゃあ、離散時間をさらに粗くしたらどうなるのっと。
時間刻みdt=0.5、すなわち離散時間=0.5の場合

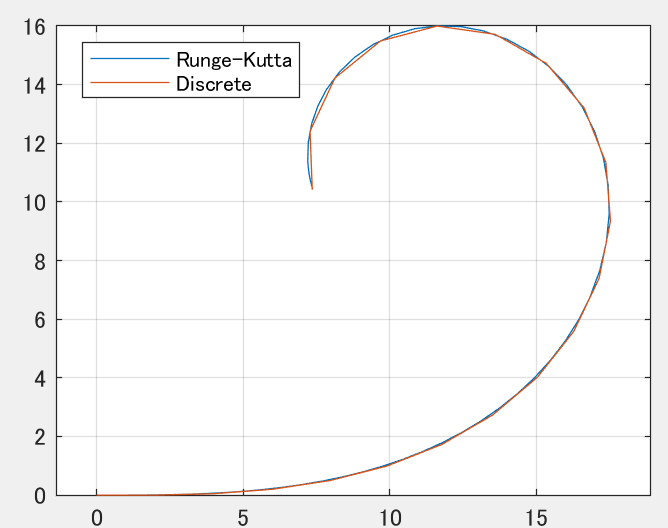
離散時間が粗すぎて線がガタガタしてきましたが、サンプリング点における誤差はそれほど大きくないという結果になりました。
うーん、離散化って本当に面倒臭い奥が深いですね。

ここで改めて強調しておきたいのですが、非線形状態方程式の離散化式において厳密式が使える場合はそれほど多くなく、基本的には妥協案を使うことになります。

ただ上記からすると厳密式を使うのは非常にメリットのあることなので、使える場合には積極的に使って行きましょう。使えるかどうかの判断には離散化後の式をよく見ることが重要です。

おわりに

お膳立てにて説明した通り、ルンゲクッタでも離散化でも同じような解を求めることはできます。
ただし重要なのは、同じような解を求めることが出来ることを知った上で一方を選択するのと、知らずに使うのとでは大きく意味が違うということです。
知らずに使った場合、研究に行き詰まる原因を自ら生み出すことになるので、できれば初期のうちに摘み取っておきたいものです。