はじめに
現代制御の代表的な手法に極配置法、状態フィードバック制御があります。
これら方法はハマれば非常に効果がある反面、古典制御と比べ理解が難しいとよく言われます。
(先日もtwitterで理屈は分かるけど、どう使ったら?という人がいた)
本稿は感覚重視で説明することで、ビギナーの理解を助けることを目的とします。
1.感覚的に理解するポイント
あなたにとって馴染みのあるもの、いつも制御しているものを題材として理解しましょう。
機械屋さんなら機械的なモノ、電気屋さんなら電気的なモノ。
下記では便宜上、機械屋さんの題材であるバネマスダンパで説明を行いますが他の系でも基本的な考え方は同じです。
2.バネマスダンパ系で見る、極配置法の考え方
バネマスダンパ系とは下記のもの。*1
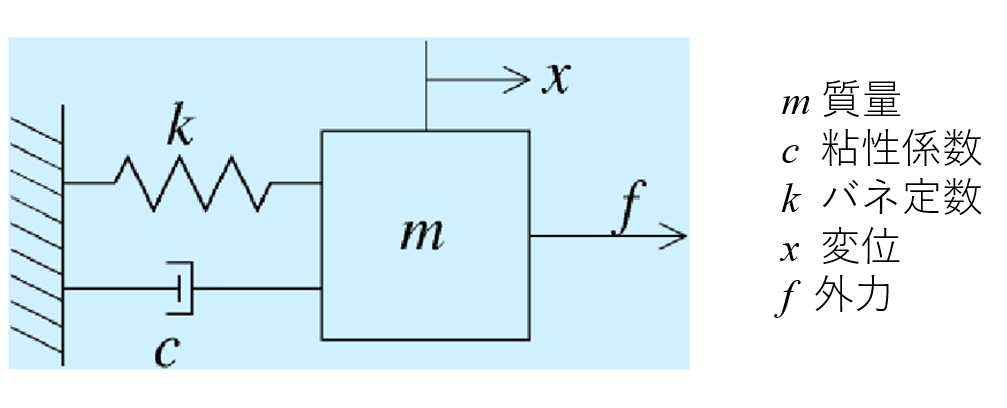

よく教科書に載っているやつですね。
とはいうものの、実際の世の中には上図そのものがない=馴染みがないので少し分かりにくいです。
バネマスダンパ系の代表例としては車のサスペンションが挙げられるので、以下ではこれで考えます。*2
車に馴染みのない方はご勘弁を。
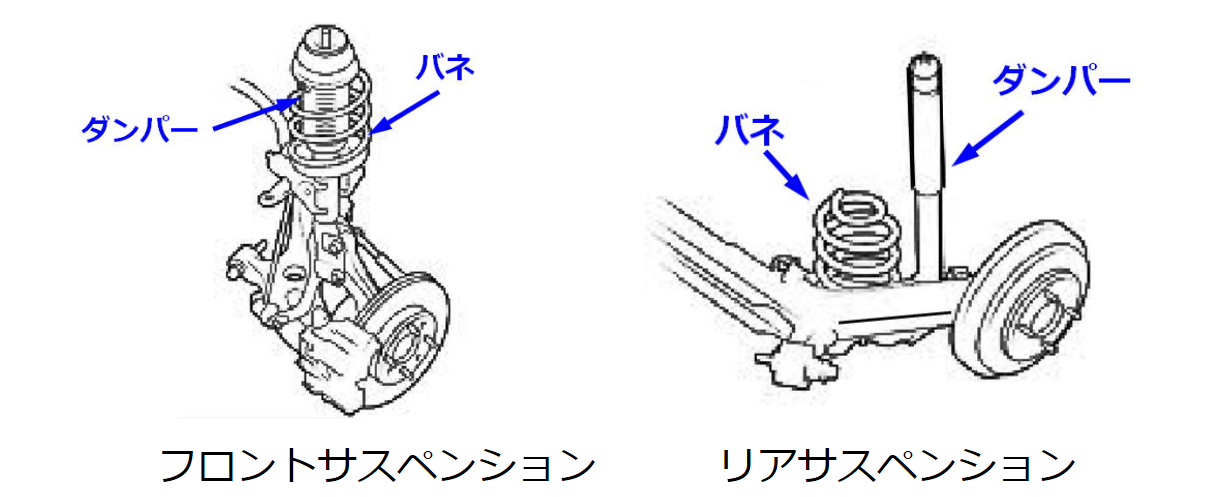
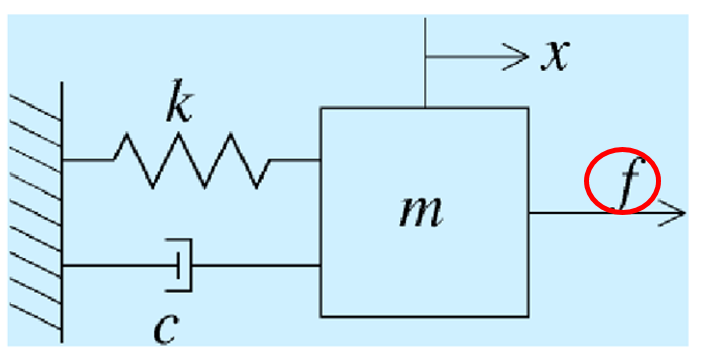
サスペンションをバネマスダンパ系に落とし込むと、バネの固さが定数kに、サスペンションより上の車体の重さが質量mに、ダンパの強さが粘性係数cになります。また車体の高さが変位xになります。
サスペンションは、ダンパを強くするほど=粘性係数cを大きくするほど振動抑制効果があります。これは、ダンパが振動を熱エネルギーとして逃がすためです。*2
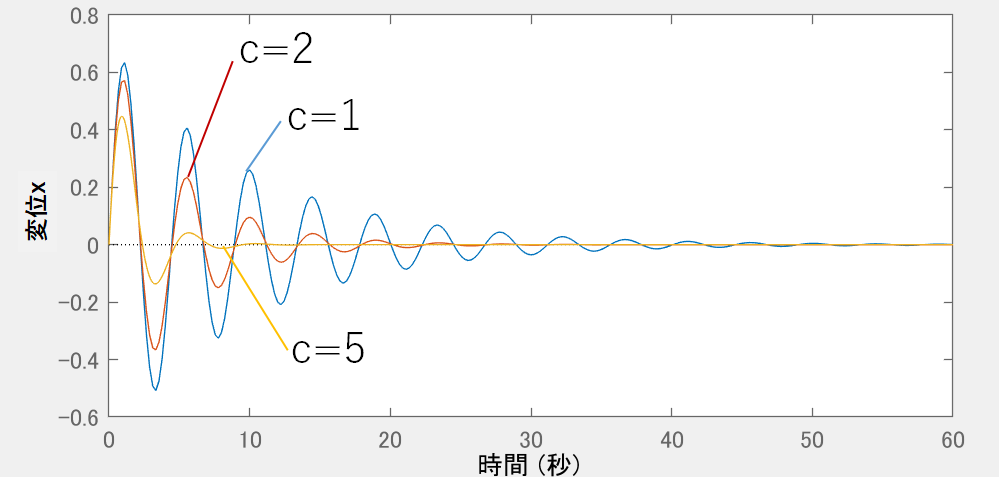
極配置法を乱暴に説明すると、サスペンションに発生する振動の大きさを、望み通りの大きさにコントロールする方法のことになります。上記は振動の大きさをダンパの強弱の調整によってコントロールを行うので、言うなれば「ダンパの調整による極配置法」です。(普通はこんな言い方しませんが)
制御する対象の挙動を望み通りに変えること=極配置なので、ダンパのみならずバネの強弱を変えること、質量を変更することも極配置に当たります。
一般に極配置法は、制御対象を安定化させる(振動しないようにさせる)ときに使います。サスペンションの極を求めると下記になります。
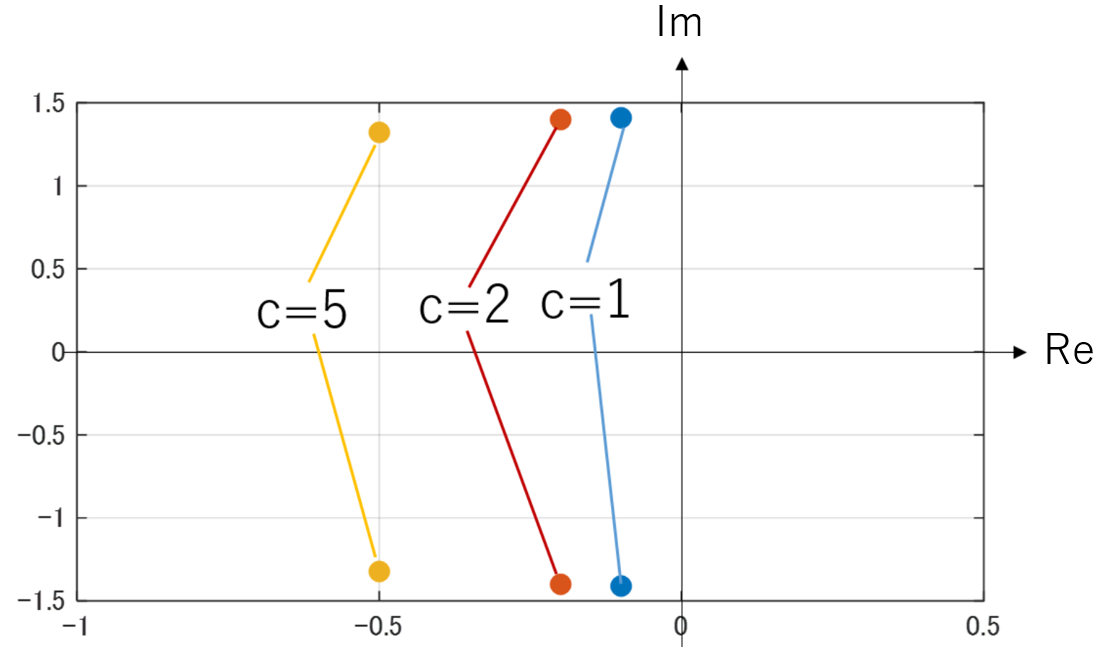
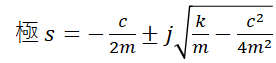
上図ではcが大きいほど極が左方向に移動しています。また数式もcが大きいほど実部は減少します。
極配置法の厳密な定義は「極を所望の位置に設定する方法」であって、振動抑制はその結果として得られるものです。しかしながら、感覚的に理解するには逆のプロセス、すなわち「振動抑制のために、極配置法を使う」のほうが収まりがよいでしょう。
また上記の図から読み取れることですが、制御の教科書によくある「極が左方向にあるほど安定」と、「サスペンションはダンパを強くさせるほど振動が収まる」は表現が違うだけで同じことです。後者を軸として考えることで、極配置を感覚的に理解しやすくなるものと思います。
なお、面白いことに振動を熱エネルギーとして逃がして振動抑制する、という考え方は、バネマスダンパ以外の系でも有効です。ここ重要。
例えばLCR回路では、抵抗Rを大きくすることで振動抑制可能で、極配置も上記と同じ結果が得られます。他の系でも同様の結果が得られるはずなので、試算してみて下さい。
3.古典制御との関係
上記の説明を見て、古典制御を学習した人であれば
「え、それって古典制御における減衰定数のことじゃないの?」と思われるかも知れません。
こういうやつ。*3
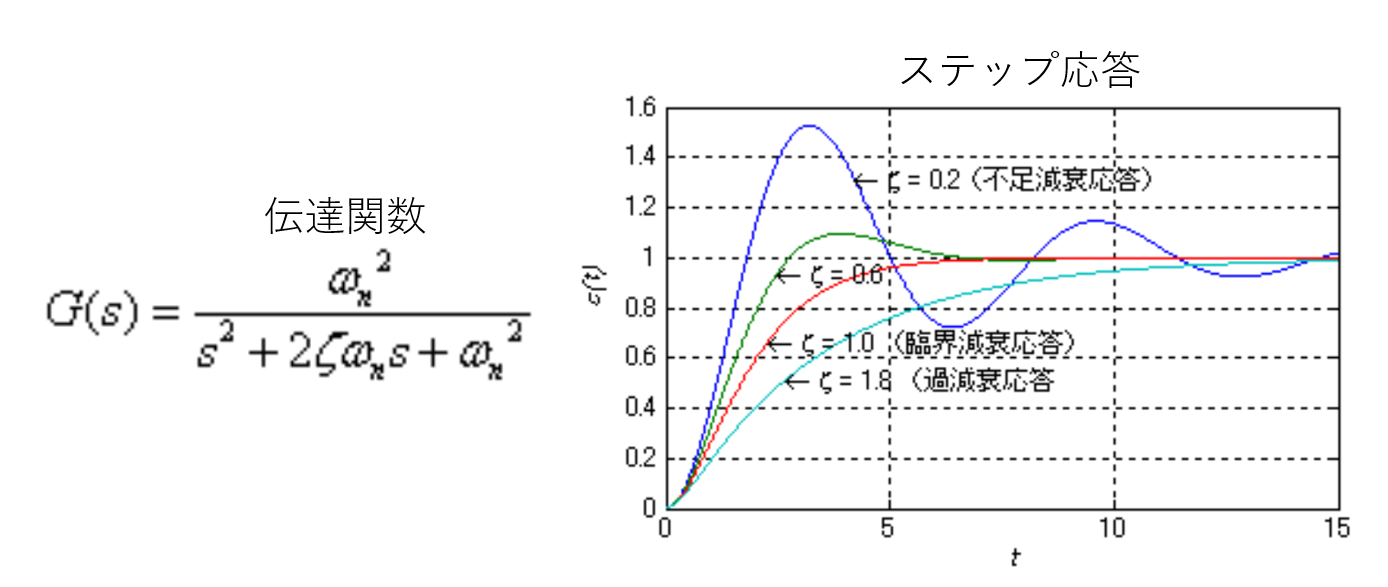
古典制御における「減衰定数が高いほど振動が収まる」も、表現が違うだけで「極が左方向にあるほど安定」と同じことです。
今回例に挙げているような2次系、単入力単出力であれば、減衰係数で考えるか極で考えるかはその人の好みでよいのではと思います。
これが4次系以上、複数入力複数出力になると、減衰定数を求めるのが困難なケースが出てくるため極で考えたほうが手っ取り早い・もしくは便利な場合が多いです。しかしながら、系の特性を感覚的に理解したいときは4次系であっても2次系に近似し、減衰定数を求めたほうが有効な場合もあります。
方法論にとらわれず、制御対象や目的によって適切な手段を選択するのが制御屋としての腕の見せ所とも言えます。
4.状態フィードバック制御による極配置法
状態フィードバック制御による極配置法を乱暴に言ってしまうと、
ハードウェアの変更なしに、ソフトウェア的に制御対象の振動を抑制する方法です。
どういうことか、再度サスペンションの例えで説明します。
サスペンションでは、ダンパを強くすることで振動抑制を行っていました。当然ながらこれには、ダンパのセッティングを変えたりダンパそのものを取り換える必要があって面倒です。
そこで、車体に与える外力fに工夫を加えることで、ダンパを変えた状態を模擬させます。
外力fを、変位xの微分値に応じて補正するものとするとブロック図は下記となります。なおKは比例ゲインです。
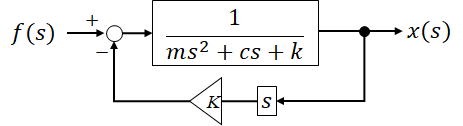
上記を変形させ、ブロック図を1つにまとめると下記になります。
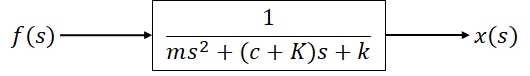
ダンパの強さc が c+Kに変化しました。これにより、ゲインKを変化させることでダンパを変えた状態を模擬することが出来ます。
上記はあえてブロック図(=古典制御)で書いていますが、状態方程式(=現代制御)でも結果は同じです。著者としてはむしろ、ブロック図表現のほうが感覚的に分かりやすくてよいことを主張したいです。ちなみ上記の図によく似た古典制御の手法に「微分先行型PID制御*4」があり、微分先行型PID制御のD項のみを使う場合と上記の図はまったく同じものになります。
個人的な見解では、極を意識してD項を使うのであれば状態フィードバック制御であり、PI制御のおまけとしてD項を使うのであれば微分先行型PID制御であるという、2面性のある制御手法なのではないかと思います。
なお上記のように、状態フィードバック制御をブロック図で分かりやすく表現できるのは制御対象が2次系、単入力単出力だからに過ぎず、4次系以上、複数入力複数出力なら状態方程式を使うのが普通と思います。ただ極配置同様、何をしているかを感覚的に表現・理解したいときは4次系以上であっても2次系に近似して考えることが有効な場合があります。ここでもやはり、制御対象や目的によって使い分けることが制御屋の腕の見せ所になります。
ここまでの内容だと、状態フィードバック制御は非常に簡単なように見えますが、実装時には色々な問題があって状態フィードバック制御をそのまま適用できない場合があります。下記によくある問題とその対処方法を記載します、読者にとってヒントになれば幸いです。
問題1:外力fを直接操作できない。
例えば、車体に加わるモータの出力電圧Vしか操作できない。
対処法:本来使いたい操作量fと、とりあえず使える操作量Vとの関係を考えてみる。
⇒ f(s) = (V(s) - ωKe)/(Ls+R) なので、逆起電力ωKeを補償した上で
R≫Lなる条件のもとf(s) ≒ V(s)/Rと近似すれば、fの代わりにVを使えるはず。
問題2:変位xの微分値を直接計測できない。
例えば、角加速度センサしか付いていない。
対処法:本来使いたいセンサ値と、とりあえず使えるセンサ値との関係を考えてみる。
⇒変位x = rsinθ であり、θ≒0ならば x ≒ rθで近似できる。
それゆえ、xの微分値の代わりに角加速度センサの積分値を使えるはず。
なおセンサにオフセット誤差がある場合は不完全積分が有効。
(同様に微分が必要な場合は不完全微分が有効な場合あり)
問題3:制御対象のモデルが分からないため、
何の情報をどこにフィードバックしてやればよいか分からない。
対処法:感覚的なアプローチで安定化の方法を考え、とりあえず試してみる。
⇒安定化するには振動エネルギーを熱として逃がせばよい事に着目する。
摩擦熱として逃がすものとすると、摩擦力を増やせれば振動抑制できそう。
摩擦力=摩擦係数×速度 なので、
速度っぽい出力にゲインをかけて力っぽい入力にフィードバックしてみる。
5.おわりに・・・制御工学はなぜ難しいか
いかがだったでしょうか。
多少は理解の助けになった、あるいは使ってみようという気になったのであれば幸いです。
制御工学が難しい理由の一つとして、制御=目に見えないものであることがよく挙げられます。しかしながら筆者は別の理由として、制御の教科書には具体的な事例が書かれておらず、理屈だけを説明しているためではないかと思います。
しかしながら事例を細々と説明すると冗長となってしまう、あるいは特定の系だけに限定した議論になってしまう。これを避けるために教科書などは事例なしで書かれています。
なので冒頭にも述べたように、馴染みのあるもの・いつも制御しているものを題材に考えてみましょう。
参考文献
*1 http://www2.kaiyodai.ac.jp/~zhang/Lesson/Seigyo_2/seigyo_Two_2_2006.pdf
*2 http://macasakr.sakura.ne.jp/T11TorqueHorsePower.html
*3 http://okawa-denshi.jp/techdoc/2-3-8nizidentatu2.htm
*4 http://arduinopid.web.fc2.com/N22.html