はじめに
JDLA E資格試験で出題される機械学習モデルの計算グラフについて解説した記事です。
E資格試験の深層学習パートでは、計算グラフを用いた計算問題や機械学習モデルの表現が登場します。
なお、他パートの具体的な解説については、下記をご覧ください。
[E資格試験に関する私の投稿記事リスト][link-1]
[link-1]:https://qiita.com/fridericusgauss/items/5a97f2645cdcefe15ce0
目次
計算グラフ
概要
本稿で言う「計算グラフ」は、機械学習モデルの学習方法をグラフ化したものです。
これは、E資格試験対策としてよく推奨されている下記の本で解説されています。
[ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装][link-2]
[link-2]:https://www.amazon.co.jp/%E3%82%BC%E3%83%AD%E3%81%8B%E3%82%89%E4%BD%9C%E3%82%8BDeep-Learning-%E2%80%95Python%E3%81%A7%E5%AD%A6%E3%81%B6%E3%83%87%E3%82%A3%E3%83%BC%E3%83%97%E3%83%A9%E3%83%BC%E3%83%8B%E3%83%B3%E3%82%B0%E3%81%AE%E7%90%86%E8%AB%96%E3%81%A8%E5%AE%9F%E8%A3%85-%E6%96%8E%E8%97%A4-%E5%BA%B7%E6%AF%85/dp/4873117585/ref=as_li_ss_tl?ie=UTF8&linkCode=sl1&tag=edom18-22&linkId=4b2403fb19573fbb63cd7294a6ee6554&language=ja_JP
計算グラフを導入することで、機械学習モデルの学習方法に関して、数式による表現をなるべく削減でき、明快に理解することができます。
定義
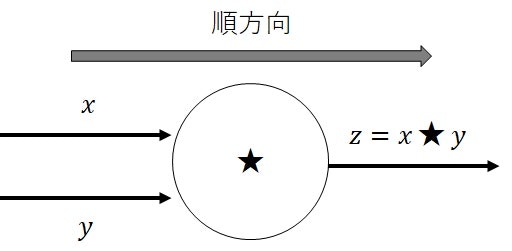
計算グラフは、下図(図1)で表されるように、ノード(点)とエッジ(矢印)
で構成されるグラフです。
 |
|---|
| 図1 |
【ルール】
計算グラフにおけるルールは下記の通りです。
- エッジは、単体の変数や数値の役割がある。
- ノードは、エッジに割り当てられた変数や数値を用いて、計算を行う役割がある。(関数による写像や二項演算子)
- ノードに向かって、エッジの矢印が入る場合、そのエッジがノードの入力(計算に使用する変数)であることを表す。
- ノードから、エッジの矢印が出る場合、そのエッジがノードの出力(計算結果)であることを表す。
- ノードの入力エッジが複数存在する場合、ノードの計算に使用する入力変数が複数あることを表す。
- ノードの出力エッジが複数存在する場合、ノードの計算結果(同じ値)がそれぞれに割り当てられる。
- ノードの出力エッジを他のノードに接続する(入力エッジとして使用する)ことで、エッジの連結が可能。
- 連結された複数のノードは、両端のエッジのみを持つ単体のエッジに置換できる。(ブラックボックス性)
つまり、__計算グラフは、変数同士の演算ルールを視覚化したもの__です。
計算グラフが与える演算ルールは、順伝播計算と逆伝播計算の二種類あります。
順伝播計算
計算グラフの左から右方向(順方向)に計算し、エッジの値を導出していくことを__順伝播計算__といいます。
順伝播計算のルールは下記の通りです。
- 左端のノードを「最初のノード」、その入力エッジを「全体の入力」、右端のノードを「最後のノード」、その出力エッジを「全体の出力」とみなす。
- 最初のノードの入力エッジを用いて、その出力エッジの数値を求める。
- 最初のノードの出力エッジを、次のノードの入力エッジとして用いて、またその出力エッジの数値を求める、というように順に計算していく。
- この計算を繰り返して、最終ノードの出力エッジを求める。
- 各ノードの計算方法は、ノードの中身で定義される。
ノードの中身によって、演算方法が多少異なります(本質的には同じですが、初学者はステップを分けて理解するのが望ましいと思われます)。
【ノードが二項演算子】
一つ目は、ノードが二項演算子の場合です。
図1の通り、ノードに二項演算子$\star:X\times Y\rightarrow Z$が定義されており、二種類の変数$x\in X,y\in Y$が入力として与えられたとき、ノードの出力$z\in Z$は、$z=x\star y$で表されることを表記します。
二項演算子$\star$としては、スカラ(実数)同士の四則演算($\star=+,-,\times,/$)か、
実数ベクトルや行列同士の演算($\star=+,-,\odot,dot$)が基本的に該当します。
$\odot$は、Hadamard積(アダマール積、Element-Wise)を表しています。
Hadamard積は同じサイズの二つのベクトルあるいは行列の二項演算子で、成分毎の積を求め、それらを要素とするベクトルあるいは行列を計算します。
【ノードが関数による写像】
二つ目は、関数による写像の場合です。
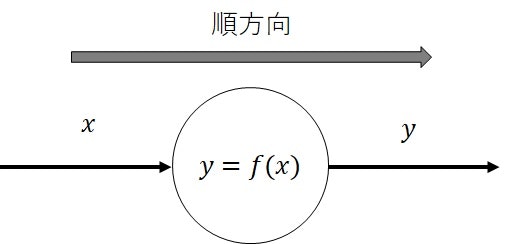
下図(図2)の通り、ノードに関数$f:X\rightarrow Y$が定義されており、変数$x\in X$が入力として与えられたとき、ノードの出力$y\in Y$は、$y=f(x)$で表されることを表記します。
 |
|---|
| 図2 |
関数$f$としては、冪関数(指数が正のときは累乗、指数が負のときは逆数)や指数関数などが使用されるため、実数を入力する関数$f:\mathbb{R}\rightarrow Y$が基本的に該当します。
出力範囲$Y$は関数$f$の種類によって異なります。
機械学習では、ロジスティック回帰や深層学習における活性化関数が多いです。
二項演算子のケースを2変数関数$f:X\times Y\rightarrow Z$と考えると、関数による写像のケースと同じ役割であることがわかります。
逆伝播計算
右から左方向(逆方向)に計算することを__逆伝播計算__といいます。
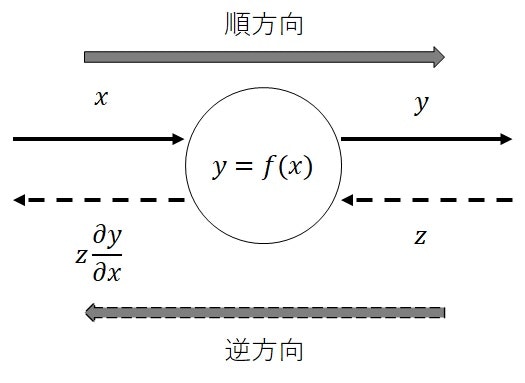
下図(図3)のように、本稿では、逆方向のエッジを破線の矢印で表し、順方向のエッジ(実線の矢印)と区別します。
 |
|---|
| 図3 |
逆伝播計算のルールは下記の通りです。
- 逆方向のエッジは、順方向のエッジに対応して存在する。
- 右端のノードを「最初のノード」、その入力エッジを「全体の入力」、左端のノードを「最後のノード」、その出力エッジを「全体の出力」とみなす。
- 最初のノードの入力エッジを用いて、その出力エッジの数値を求める。
- 最初のノードの出力エッジを、次のノードの入力エッジとして用いて、またその出力エッジの数値を求める、というように順に計算していく。
- この計算を繰り返して、最終ノードの出力エッジを求める。
【入出力エッジがスカラの場合】
入出力エッジがスカラの場合のルールは下記の通りです。
- 各単体ノードの出力は、順伝播側の出力$y$を入力$x$で偏微分したもの(局所微分)を、逆伝播側の入力$z$に掛けたもの$z\frac{\partial y}{\partial x}$とする。(逆変換$f^{-1}$ではないことに注意)
- 最初のノードの入力エッジは基本的に$1$とする。
特に、多くの機械学習における学習では、逆伝播計算が必要なので、E資格試験においても頻出です。
機械学習では、__順伝播計算が、ある入力に対応するモデルの出力と、学習データの誤差を計算するプロセスに該当__することに対して、__逆伝播計算が、学習過程で必要となる誤差関数$L$の勾配を計算するプロセスに該当__します。
逆伝播計算における勾配計算では、誤差関数に対するモデルパラメータの変動が必要ですが、一般に解析的に求められません。
そこで、順伝播計算で導出された各エッジの値(局所微分)を使用し、ノードに沿って伝播させる(連鎖微分)ことで、全体の勾配を数値的に求めることが可能です。
ニューラルネットワークの誤差逆伝播法は、これを繰り返すことでモデルを学習する方法です。
また、ルールの最後の項目について補足します。
逆伝播側の最初のノードの入力エッジは$1$としますが、このとき、計算グラフ上で何が伝播するのかがわかりにくいです。
これは、機械学習モデルを計算グラフで表現した場合をイメージすると、伝播のイメージがわかりやすくなります。
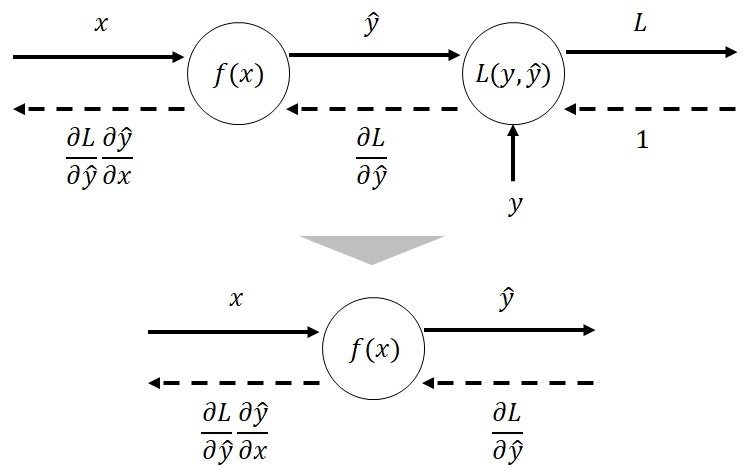
機械学習モデルでは、下図(図4)の形式の計算グラフを構成する場合が多いです。
 |
|---|
| 図4 |
左側のノードが機械学習が学習するモデル$f$で、右側のノードが誤差関数$L$です。
左側のノードでは、説明変数$x$を入力エッジとし、目的変数に該当するモデルの出力$\hat{y}=f(x)$を出力エッジとします。
右側のノードでは、モデル出力$\hat{y}$と正解データの$y$を入力エッジとし、それらの誤差$L=L(y,\hat{y})$を出力エッジとします。
このとき、誤差関数$L$に該当するノードを省略し、右端のノードの逆伝播計算時の入力エッジを$\frac{\partial L}{\partial \hat{y}}$と割り当てることがあります。
このため、逆伝播計算では、右端のノードに誤差を入力し、左端へと伝播していくイメージとなります。
【入出力エッジが行列の場合】
入出力エッジが行列の場合はもう少し複雑になります。
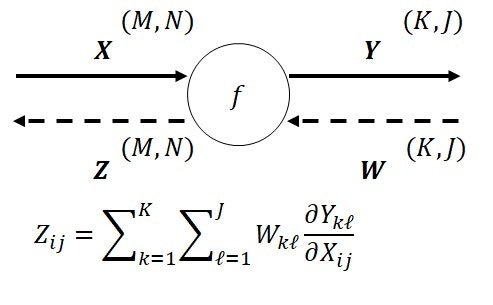
順伝播時の入力エッジが$\boldsymbol{X}\in \mathbb{R}^{M\times N}$、出力エッジが$\boldsymbol{Y}\in \mathbb{R}^{K\times J}$とし、逆伝播時の入力エッジが$\boldsymbol{W}\in \mathbb{R}^{K\times J}$、出力エッジが$\boldsymbol{Z}\in \mathbb{R}^{M\times N}$とします。
ノードは$f:\mathbb{R}^{M\times N} \rightarrow \mathbb{R}^{K\times J}$です。
行列の場合の計算グラフは下図(図5)の通りです。
 |
|---|
| 図5 |
入出力エッジが行列の場合のルールは下記の通りです。
- 逆伝播時の出力エッジ$\boldsymbol{Z}$の各成分$Z_{ij}$は、式(1)で表される。
\begin{align}
Z_{ij}=\sum_{k=1}^{K}\sum_{\ell=1}^{J}W_{k\ell} \frac{\partial Y_{k\ell}}{\partial X_{ij}}
\end{align}
\tag{1}
式(1)は、順伝播時の出力エッジ$\boldsymbol{Y}$の各成分$(k,\ell)$について、スカラの場合と同様の式を計算し、それを全ての要素について和をとった形式となっています。
__機械学習で扱う変数やデータは、基本的にベクトルや行列ですので、覚えるのは必須__です。
ただし、行列の場合、$f$は二項演算子である場合がほとんどですので、これはあくまで一般化したものです。
$f$は二項演算子となる具体例については、次の章で説明します。
計算グラフの基本例
スカラの四則演算
スカラの四則演算($\star=+,-,\times,/$)の場合の計算グラフです。
入力エッジが$x,y\in \mathbb{R}$、出力エッジが$z\in \mathbb{R}$とします。
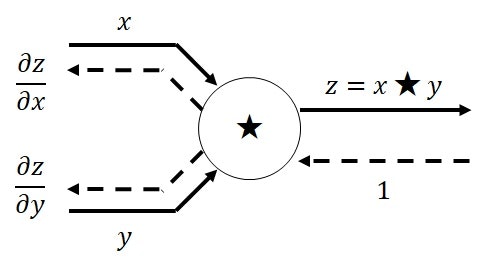
下図(図6)がスカラの四則演算の計算グラフです。
 |
|---|
| 図6 |
順伝播計算は、$z=x\star y$です。
逆伝播計算は、$x$側のエッジが$\frac{\partial z}{\partial x}$、$y$側のエッジが$\frac{\partial z}{\partial y}$です。
これは、図3のルールに従っているだけです。
具体的な式は演算子毎で異なりますが、本稿では割愛します。
シグモイド関数
シグモイド関数の場合の計算グラフです。
シグモイド関数$\sigma$は、式(2)で表されます。
\begin{align}
\sigma(x) &= \frac{1}{1+\exp(-x)} \\
&= (1 + \exp((-1)\times (x)))^{-1}
\end{align}
\tag{2}
シグモイド関数は、分解して表現し直すと、和・積の二項演算、指数関数や冪関数(逆数)の合成関数です。
これを踏まえて、シグモイド関数の順伝播と逆伝播を求めます。
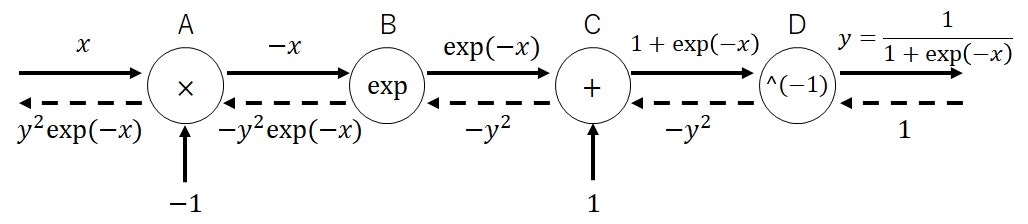
下図(図7)がシグモイド関数の計算グラフです。
 |
|---|
| 図7 |
合成関数なので、各演算・変換を順にA、B、C、Dと呼ぶことにし、最後の出力は$y$とします。
これは、計算グラフにおけるノードに該当します。
下記では、数式ベースで各ノードの計算を確認していきます。
順伝播計算における各ノードの出力エッジは、式(3)で表されます。
\begin{align}
&ノードA: -x \\
&ノードB: \exp(-x)\\
&ノードC: 1+\exp(-x)\\
&ノードD: \frac{1}{1+\exp(-x)} = y
\end{align}
\tag{3}
逆伝播計算における各ノードの出力エッジは、式(4)で表されます。
\begin{align}
&ノードA: y^{2}\exp(-x)=y(1-y)\\
&ノードB: -y^{2}\exp(-x)\\
&ノードC: -y^{2}\\
&ノードD: -y^{2}
\end{align}
\tag{4}
【折り畳み】式(3)の導出
【折り畳み】式(4)の導出
行列の和
行列の和の場合の計算グラフです。
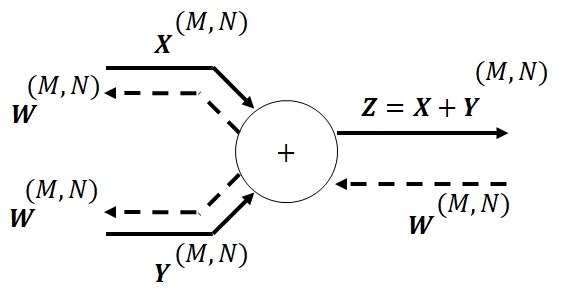
順伝播時の入力エッジが$\boldsymbol{X},\boldsymbol{Y}\in \mathbb{R}^{M\times N}$、出力エッジが$\boldsymbol{Z}\in \mathbb{R}^{M\times N}$とし、逆伝播時の入力エッジが$\boldsymbol{W}\in \mathbb{R}^{M\times N}$とします。
下図(図8)が行列の和の計算グラフです。
 |
|---|
| 図8 |
下記では、数式ベースで各エッジの計算を確認していきます。
順伝播計算における出力エッジは、$\boldsymbol{Z}=\boldsymbol{X}+\boldsymbol{Y}$です。
逆伝播計算における各出力エッジは、式(5)で表されます。
\begin{align}
&エッジ\boldsymbol{X}:\boldsymbol{W}\\
&エッジ\boldsymbol{Y}:\boldsymbol{W}
\end{align}
\tag{5}
【折り畳み】式(5)の導出
行列の積
行列の積($dot$)の計算グラフです。
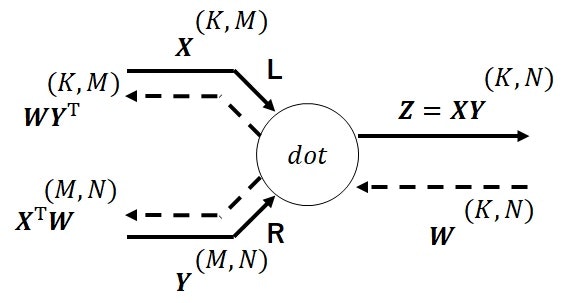
入力エッジが$\boldsymbol{X}\in \mathbb{R}^{K\times M},\boldsymbol{Y}\in \mathbb{R}^{M\times N}$、出力エッジが$\boldsymbol{Z}\in \mathbb{R}^{K\times N}$とし、逆伝播時の入力エッジが$\boldsymbol{W}\in \mathbb{R}^{K\times N}$とします。
下図(図9)が行列の積の計算グラフです。
 |
|---|
| 図9 |
なお、行列の積は可換でないため、左からの積を表すエッジにはL、右からの積を表すエッジにはRと記し、順序を明確にしておきます。
下記では、数式ベースで各エッジの計算を確認していきます。
順伝播計算における出力エッジは、$\boldsymbol{Z}=\boldsymbol{X}\boldsymbol{Y}$です。
逆伝播計算における各出力エッジは、式(6)で表されます。
\begin{align}
&エッジ\boldsymbol{X}:\boldsymbol{W}\boldsymbol{Y}^{\mathrm{T}}\\
&エッジ\boldsymbol{Y}:\boldsymbol{X}^{\mathrm{T}}\boldsymbol{W}
\end{align}
\tag{6}
【折り畳み】式(6)の導出
より詳細な説明は、下記記事が参考になります。
[[DeepLearning] 計算グラフについて理解する][link-3]
[link-3]:https://qiita.com/edo_m18/items/7c95593ed5844b5a0c3b
ロジスティック回帰モデルへの適用
ロジスティック回帰モデル
下記記事では、ロジスティック回帰モデルとその学習方法について、数式ベースで解説しました。
[ロジスティック回帰][link-4]
本章では、ロジスティック回帰を計算グラフで表現し、計算が容易に得られることを確認します。
目的変数(モデルの出力)$\hat{y}\in \mathbb{R}$、説明変数$\boldsymbol{x}=(x_1,\cdots,x_M)^{\mathrm{T}}\in \mathbb{R}^{M}$としたとき、ロジスティック回帰モデルは式(7)で表されます。
\hat{y}=\sigma(\boldsymbol{w}^{\mathrm{T}}\boldsymbol{x}+w_{0})
\tag{7}
ただし、モデルパラメータは$\boldsymbol{w}=(w_1,\cdots,w_M)^{\mathrm{T}}\in \mathbb{R}^{M}, w_0\in \mathbb{R}$です。
$\sigma: \mathbb{R} \rightarrow \mathbb{R}$はシグモイド関数(式(2))です。
$\boldsymbol{x}^{\prime}=(x_1,\cdots,x_M,1)^{\mathrm{T}}\in \mathbb{R}^{M+1}$、$\boldsymbol{w}^{\prime}=(w_1,\cdots,w_M, w_0)^{\mathrm{T}}\in \mathbb{R}^{M+1}$としたとき、式(7)は式(8)で書き換えられます。
\hat{y}=\sigma(\boldsymbol{w}^{\prime \mathrm{T}}\boldsymbol{x}^{\prime})
\tag{8}
学習データ$D=\{(\boldsymbol{x}^{\prime}_{1}, y_{1}),\cdots,(\boldsymbol{x}^{\prime}_{N}, y_{N})\}$とすると、説明変数の学習データ$\boldsymbol{X}$に対するモデルの出力$\boldsymbol{\hat{y}}\in \mathbb{R}^{N}$は、式(9)で表されます。
\begin{align}
\boldsymbol{\hat{y}}
&=\sigma(\boldsymbol{X}\boldsymbol{w}^{\prime})\\
&=(\sigma(\boldsymbol{w}^{\prime \mathrm{T}}\boldsymbol{x}^{\prime}_{1}),\cdots,\sigma(\boldsymbol{w}^{\prime \mathrm{T}}\boldsymbol{x}^{\prime}_{N}))^{\mathrm{T}}\\
&=(\hat{y}_{1},\cdots,\hat{y}_{N})^{\mathrm{T}}
\end{align}
\tag{9}
\begin{align}
\boldsymbol{X}=(\boldsymbol{x}^{\prime}_{1},\cdots,\boldsymbol{x}^{\prime}_{N})^{\mathrm{T}}\in \mathbb{R}^{N\times (M+1)}
\end{align}
ただし、式(9)の1行目の$\sigma$は、$\sigma: \mathbb{R}^{N} \rightarrow \mathbb{R}^{N}$で、各要素に対して別々にシグモイド関数を作用する関数です。
誤差関数$L$は2値クロスエントロピー誤差関数(負の対数尤度)なので、式(10)で表されます。
L(\boldsymbol{\hat{y}},\boldsymbol{y})=-\sum_{n=1}^{N}\left(y_{n}\ln(\hat{y}_{n})+(1-y_{n})\ln(1-\hat{y}_{n})\right)
\tag{10}
\begin{align}
&\boldsymbol{y}=(y_{1},\cdots,y_{N})^{\mathrm{T}}\in \mathbb{R}^{N}\\
\end{align}
計算グラフ(誤差関数のノード除外)
前述の通り、機械学習モデルを計算グラフで表現する場合、右端のノードを誤差関数$L$とし、その出力エッジを学習データとの誤差とするのが一般的ですが、まずは__誤差関数のノードを除き、モデルの出力を最後の出力エッジとするケース__を考えます。
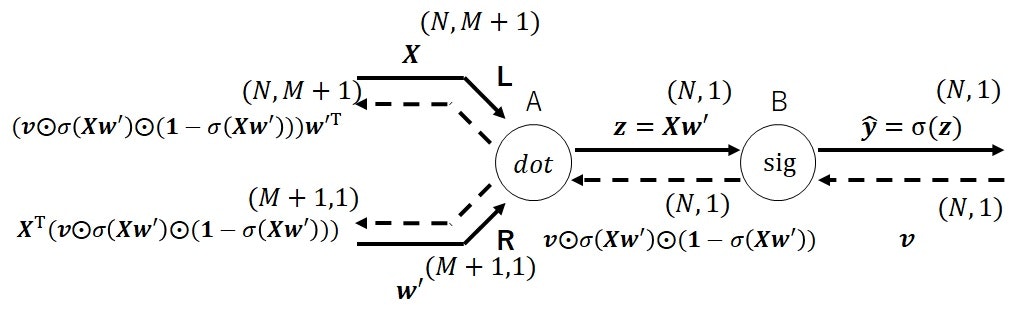
順伝播時の入力エッジが$\boldsymbol{X}\in \mathbb{R}^{N\times (M+1)}, \boldsymbol{w}^{\prime} \in \mathbb{R}^{M+1}$、出力エッジが$\boldsymbol{\hat{y}}\in \mathbb{R}^{N}$とし、逆伝播時の入力エッジが$\boldsymbol{v}\in \mathbb{R}^{N}$とします。
下図(図10)がロジスティック回帰(誤差関数のノード除外)の計算グラフです。
 |
|---|
| 図10 |
なお、各ノードを左から順にA、Bと呼ぶことにします。
ノードBはシグモイド関数を作用するノードで、図7の連結されたノードを一つのノードに凝縮したものです。
下記では、数式ベースで各エッジの計算を確認していきます。
順伝播計算における各ノードの出力エッジは、式(11)で表されます。
\begin{align}
&ノードA: \boldsymbol{X}\boldsymbol{w}^{\prime} \\
&ノードB: \sigma(\boldsymbol{X}\boldsymbol{w}^{\prime}) = \boldsymbol{\hat{y}}
\end{align}
\tag{11}
逆伝播計算における各ノードの出力エッジは、式(12)で表されます。
\begin{align}
&ノードA、エッジ\boldsymbol{X}: (\boldsymbol{v} \odot \sigma(\boldsymbol{X}\boldsymbol{w}^{\prime}) \odot (\boldsymbol{1}-\sigma(\boldsymbol{X}\boldsymbol{w}^{\prime})))\boldsymbol{w}^{\prime \mathrm{T}}\\
&ノードA、エッジ\boldsymbol{w}^{\prime}: \boldsymbol{X}^{\mathrm{T}}
(\boldsymbol{v} \odot \sigma(\boldsymbol{X}\boldsymbol{w}^{\prime}) \odot (\boldsymbol{1}-\sigma(\boldsymbol{X}\boldsymbol{w}^{\prime})))\\
&ノードB: \boldsymbol{v} \odot \sigma(\boldsymbol{X}\boldsymbol{w}^{\prime}) \odot (\boldsymbol{1}-\sigma(\boldsymbol{X}\boldsymbol{w}^{\prime}))
\end{align}
\tag{12}
ただし、式(11)、式(12)の$\sigma$は、$\sigma: \mathbb{R}^{N} \rightarrow \mathbb{R}^{N}$で、各要素に対して別々にシグモイド関数を作用する関数で、$\boldsymbol{1}$は$(1,1,\cdots,1)^{\mathrm{T}}\in \mathbb{R}^{N}$です。
計算グラフ(誤差関数のノード含む)
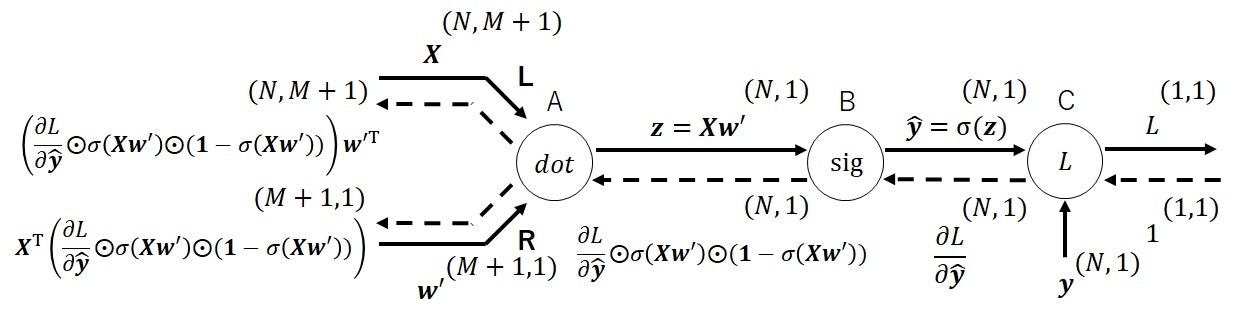
次に、右端に誤差関数のノードを連結した計算グラフを考えます。
順伝播時の入力エッジが$\boldsymbol{X}\in \mathbb{R}^{N\times (M+1)}, \boldsymbol{w}^{\prime} \in \mathbb{R}^{M+1}$、出力エッジが$L \in \mathbb{R}$とし、逆伝播時の入力エッジが$1$とします。
下図(図11)がロジスティック回帰(誤差関数のノード含む)の計算グラフです。
 |
|---|
| 図11 |
下記では、数式ベースで各エッジの計算を確認していきます。
順伝播計算における各ノードの出力エッジは、式(13)で表されます。
\begin{align}
&ノードA: \boldsymbol{X}\boldsymbol{w}^{\prime} \\
&ノードB: \sigma(\boldsymbol{X}\boldsymbol{w}^{\prime}) = \boldsymbol{\hat{y}}\\
&ノードC: -\sum_{n=1}^{N}\left(y_{n}\ln(\hat{y}_{n})+(1-y_{n})\ln(1-\hat{y}_{n})\right) = L
\end{align}
\tag{13}
逆伝播計算における各ノードの出力エッジは、式(14)で表されます。
\begin{align}
&ノードA、エッジ\boldsymbol{X}: \left(\frac{\partial L}{\partial \boldsymbol{\hat{y}}} \odot \sigma(\boldsymbol{X}\boldsymbol{w}^{\prime}) \odot (\boldsymbol{1}-\sigma(\boldsymbol{X}\boldsymbol{w}^{\prime}))\right)\boldsymbol{w}^{\prime \mathrm{T}}\\
&ノードA、エッジ\boldsymbol{w}^{\prime}: \boldsymbol{X}^{\mathrm{T}}
\left(\frac{\partial L}{\partial \boldsymbol{\hat{y}}} \odot \sigma(\boldsymbol{X}\boldsymbol{w}^{\prime}) \odot (\boldsymbol{1}-\sigma(\boldsymbol{X}\boldsymbol{w}^{\prime}))\right)\\
&ノードB: \frac{\partial L}{\partial \boldsymbol{\hat{y}}} \odot \sigma(\boldsymbol{X}\boldsymbol{w}^{\prime}) \odot (\boldsymbol{1}-\sigma(\boldsymbol{X}\boldsymbol{w}^{\prime}))\\
&ノードC: \frac{\partial L}{\partial \boldsymbol{\hat{y}}}
\end{align}
\tag{14}
式(14)のノードA、エッジ$\boldsymbol{w}^{\prime}$に逆伝播してくるものは、ロジスティック回帰の最尤推定法において求めたい勾配ベクトル$\frac{\partial L}{\partial \boldsymbol{w}^{\prime}}$です。
何度も述べているように、これはノードCの局所微分に対して、各ノードの局所微分をかけて、左端に伝播させることで、入力に対する偏微分を得るという、連鎖律を利用しています。
【折り畳み】式(14)の導出
$\frac{\partial L}{\partial \boldsymbol{\hat{y}}}$は、式(15)で表されます。
\begin{align}
&\frac{\partial L}{\partial \hat{y}_{i}}\\
&=-\frac{\partial }{\partial \hat{y}_{i}}\sum_{n=1}^{N}\left(y_{n}\ln(\hat{y}_{n})+(1-y_{n})\ln(1-\hat{y}_{n})\right)\\
&=-\frac{y_{i}}{\hat{y}_{i}}+\frac{1-y_{i}}{1-\hat{y}_{i}}\\
&=\frac{-y_{i}(1-\hat{y}_{i})+\hat{y}_{i}(1-\hat{y}_{i})}{\hat{y}_{i}(1-\hat{y}_{i})}\\
&=-\frac{y_{i}-\hat{y}_{i}}{\hat{y}_{i}(1-\hat{y}_{i})}
\end{align}
\tag{15}
$\frac{\partial L}{\partial (\boldsymbol{X}\boldsymbol{w}^{\prime})}$は、式(16)で表されます。
\begin{align}
&\frac{\partial L}{\partial (\boldsymbol{X}\boldsymbol{w}^{\prime})}\\
&=\frac{\partial L}{\partial \boldsymbol{\hat{y}}} \odot \boldsymbol{\hat{y}} \odot (\boldsymbol{1}-
\boldsymbol{\hat{y}})\\
&=\left(\frac{\partial L}{\partial \hat{y}_{1}}\hat{y}_{1}(1-\hat{y}_{1}),\cdots,\frac{\partial L}{\partial \hat{y}_{N}}\hat{y}_{N}(1-\hat{y}_{N})\right)^{\mathrm{T}}\\
&=\left(-\frac{y_{1}-\hat{y}_{1}}{\hat{y}_{1}(1-\hat{y}_{1})}\hat{y}_{1}(1-\hat{y}_{1}),\cdots,-\frac{y_{N}-\hat{y}_{N}}{\hat{y}_{N}(1-\hat{y}_{N})}\hat{y}_{N}(1-\hat{y}_{N})\right)^{\mathrm{T}}\\
&=(-(y_{1}-\hat{y}_{1}),\cdots,-(y_{N}-\hat{y}_{N}))^{\mathrm{T}}\\
&=-(\boldsymbol{y}-\boldsymbol{\hat{y}})
\end{align}
\tag{16}
よって、勾配ベクトル$\frac{\partial L}{\partial \boldsymbol{w}^{\prime}}$は、式(17)で表されます。
\begin{align}
\frac{\partial L}{\partial \boldsymbol{w}^{\prime}}
&=\boldsymbol{X}^{\mathrm{T}}\frac{\partial L}{\partial (\boldsymbol{X}\boldsymbol{w}^{\prime})}\\
&=-\boldsymbol{X}^{\mathrm{T}}(\boldsymbol{y}-\boldsymbol{\hat{y}})\\
&=-\boldsymbol{X}^{\mathrm{T}}\boldsymbol{\delta}
\end{align}
\tag{17}
ただし、$\boldsymbol{\delta}=\boldsymbol{y}-\boldsymbol{\hat{y}}$は誤差です。
式(17)が下記記事の式(15)と一致しています。
[ロジスティック回帰][link-4]
上記記事で述べたように、学習では、
順伝播と逆伝播によって勾配ベクトル$\frac{\partial L}{\partial \boldsymbol{w}^{\prime}}$を得て、式(18)の式でモデルパラメータ$\boldsymbol{w}^{\prime}$を更新していきます。
\begin{align}
\boldsymbol{w}^{\prime}:=\boldsymbol{w}^{\prime}-\eta
\frac{\partial L}{\partial \boldsymbol{w}^{\prime}}
\end{align}
\tag{18}
ただし、$\eta>0$は学習率です。
このため、計算グラフを用いることで、勾配ベクトルを求める過程が視覚的にわかりやすくなります。
ニューラルネットワークへの適用
準備中。
おわりに
E資格向けの強化学習の基礎について解説しました。
なお、上記は、2021年2月時点における内容であることにご注意ください。
[E資格試験に関する私の投稿記事リスト][link-1]