ローパスフィルタとPD制御の深堀

ローパスフィルタとPD制御の関係性を深堀していく中で学んだこと・気づけたことをまとめる．

ローパスフィルタ（Low-Pass Filter）について

よく聞くやつ．一次のものと二次のものが有名．
抵抗やキャパシタ，コイルなどの電子部品を使うと構成できるという文脈が有名．
電子部品で構成すればアナログ回路になって連続系になるが，CPUで処理するデジタル回路だと離散系であり0でないサンプリング時間が存在することに注意する．

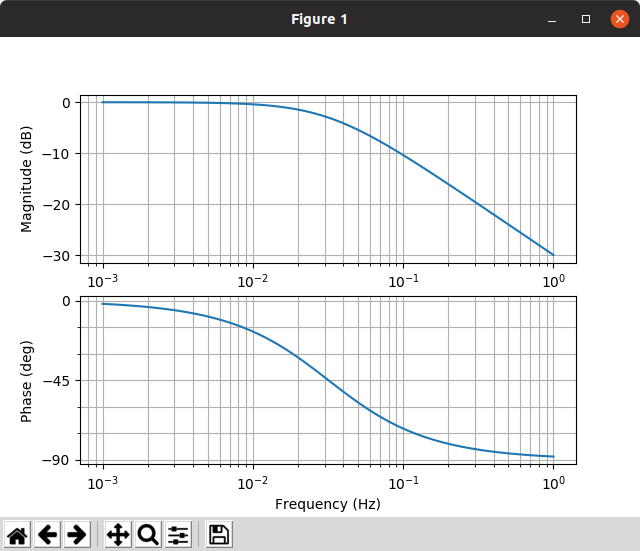
一次（first order）のローパスフィルタ

時定数$T$というパラメータがあるフィルタであって，周波数領域では

\frac{1}{1 + Ts}

で表されるフィルタである．

#!/usr/bin/env python3
import control
import control.matlab
from matplotlib import pyplot as plt

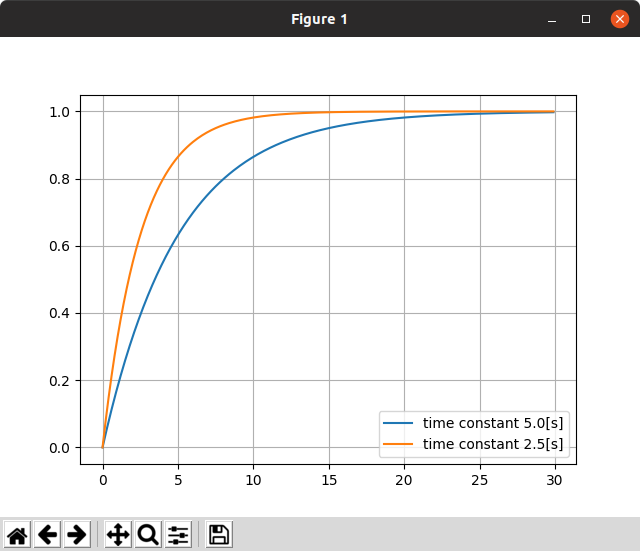
time_constant = 5.0
G = control.tf([0, 1], [time_constant, 1])
control.matlab.bode(G)
plt.show()

時定数$T = 5.0[s]$のときはカットオフ周波数は$f = \frac{1}{2 \pi T} = 3 * 10^{-2}[Hz]$となる．

#!/usr/bin/env python3
import control
import control.matlab
from matplotlib import pyplot as plt
from numpy import arange

time_constant = 5.0
G_slow = control.tf([0, 1], [time_constant, 1])
time_constant = 2.5
G_fast = control.tf([0, 1], [time_constant, 1])

(y_slow, T_slow) = control.matlab.step(G_slow, T=arange(0, 30, 0.1))
(y_fast, T_fast) = control.matlab.step(G_fast, T=arange(0, 30, 0.1))

plt.plot(T_slow, y_slow, label="time constant 5.0[s]")
plt.plot(T_fast, y_fast, label="time constant 2.5[s]")
plt.legend()
plt.grid()
plt.show()

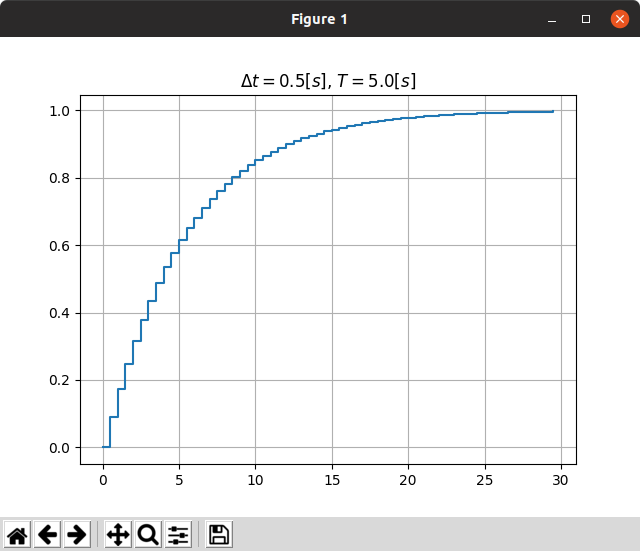
これをデジタル回路で使うには，離散化する必要がある．
時刻$t = k$のときのローパスフィルタへの入力データを$x[k]$，その時刻でのローパスフィルタの出力を$y[k]$として表すと，

\begin{align}
& \frac{Y}{X} = \frac{1}{1 + Ts}\\
\Leftrightarrow& (1 + Ts) Y = X\\
\Leftrightarrow& Y + T sY = X
\end{align}

なので，微分に後方差分を使うとすると

\begin{align}
&y[k] + T \frac{y[k] - y[k-1]}{\Delta t} = x[k]\\
\Leftrightarrow & y[k] = \frac{T}{T + \Delta t} y[k-1] + \frac{\Delta t}{T + \Delta t} x[k]
\end{align}

となる．

#!/usr/bin/env python3
import control
import control.matlab
from matplotlib import pyplot as plt
from numpy import arange

time_constant = 5.0
sampling_time = 0.5

time_list = arange(0, 30, sampling_time)
x_k = 1.0
for idx, t in enumerate(time_list):
    if idx == 0:
        y_list = [0]
        continue
    output = time_constant / (time_constant + sampling_time) * y_list[idx - 1] + sampling_time / (time_constant + sampling_time) * x_k
    y_list.append(output)

plt.plot(time_list, y_list, drawstyle="steps-post")
plt.title(r"$\Delta t = 0.5[s]$, $T = 5.0[s]$")
plt.grid()
plt.show()

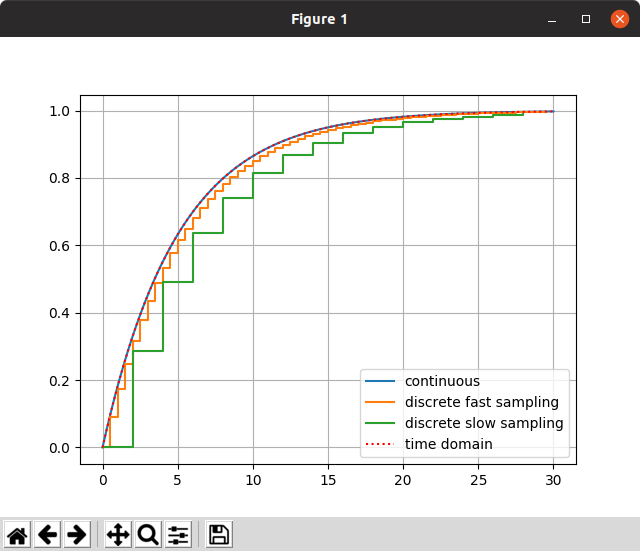
次に，時間領域で考える．ステップ応答をラプラス変換すると$\frac{1}{s}$なので，ローパスフィルタ後の出力を周波数領域で表すと

\frac{1}{1 + Ts}\frac{1}{s} = \frac{1}{s} - \frac{1}{s + \frac{1}{T}}

となる．
これを逆ラプラス変換すると

y(t) = 1 - \mathrm{e}^{-\frac{t}{T}}

となる．

#!/usr/bin/env python3
import control
import control.matlab
from matplotlib import pyplot as plt
from numpy import arange
import math

time_constant = 5.0
coarse_time_list = arange(0, 30, 0.001)

G = control.tf([0, 1], [time_constant, 1])
(y_c, T) = control.matlab.step(G, T=coarse_time_list)


def discrete(sampling_time, time_list):
    x_k = 1.0
    for idx, t in enumerate(time_list):
        if idx == 0:
            y_d = [0]
            continue
        output = time_constant / (time_constant + sampling_time) * y_d[idx - 1] + sampling_time / (time_constant + sampling_time) * x_k
        y_d.append(output)
    return y_d

y_a = [1 - math.exp(-1 * t / time_constant) for t in coarse_time_list]

plt.plot(T, y_c, label="continuous")
sampling_time_fast = 0.5
sample_time_fast_list = arange(0, 30, sampling_time_fast)
plt.plot(sample_time_fast_list, discrete(sampling_time_fast, sample_time_fast_list), label="discrete fast sampling", drawstyle="steps-post")
sampling_time_slow = 2.0
sample_time_slow_list = arange(0, 30, sampling_time_slow)
plt.plot(sample_time_slow_list, discrete(sampling_time_slow, sample_time_slow_list), label="discrete slow sampling", drawstyle="steps-post")
plt.plot(coarse_time_list, y_a, label="time domain", linestyle="dotted", c="red")

plt.legend()
plt.grid()
plt.show()

二次（second order）のローパスフィルタ

固有角振動数$\omega_n$と減衰比$\zeta$をパラメータに持つフィルタであって，周波数領域では

\frac{\omega_n^2}{s^2 + 2 \zeta \omega_n s + \omega_n^2}

で表されるフィルタである．

#!/usr/bin/env python3
import control
import control.matlab
from matplotlib import pyplot as plt

time_constant = 5.0
natural_freq = 1 / time_constant
damping_ratio = 1.0
G_first = control.tf([0, 1], [time_constant, 1])
G_second = control.tf([0, 0, natural_freq**2], [1, 2 * damping_ratio * natural_freq, natural_freq**2])
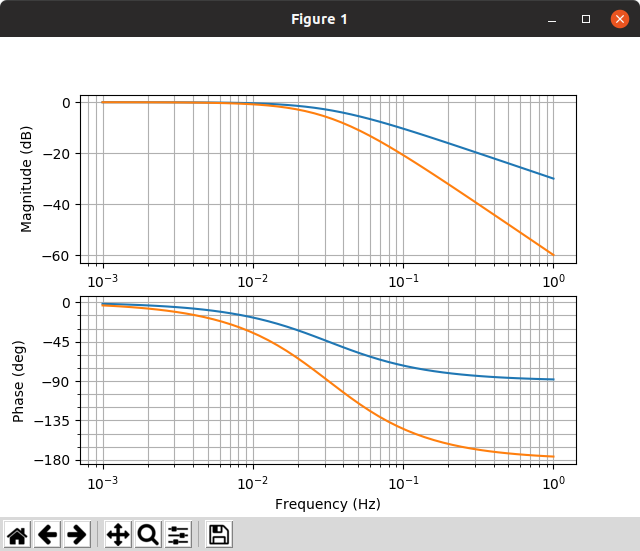
control.matlab.bode(G_first)
control.matlab.bode(G_second)
plt.show()

一次のフィルタよりも高周波のゲインが小さくなっているが，位相はより遅れるようになっていることが分かる．

#!/usr/bin/env python3
import control
import control.matlab
from matplotlib import pyplot as plt
import numpy

time_constant = 5.0
natural_freq = 1 / time_constant
damping_ratio = 1.0
G_first = control.tf([0, 1], [time_constant, 1])
G_second = control.tf([0, 0, natural_freq**2], [1, 2 * damping_ratio * natural_freq, natural_freq**2])

time_list = numpy.arange(0, 30, 0.1)
sin_one_cycle = 10.0
sin_omega = 1 / sin_one_cycle
sin_curve = 10 * numpy.sin(2 * numpy.pi * sin_omega * time_list)

(y_first, T_first, _) = control.matlab.lsim(G_first, U=sin_curve, T=time_list)
(y_second, T_second, _) = control.matlab.lsim(G_second, U=sin_curve, T=time_list)

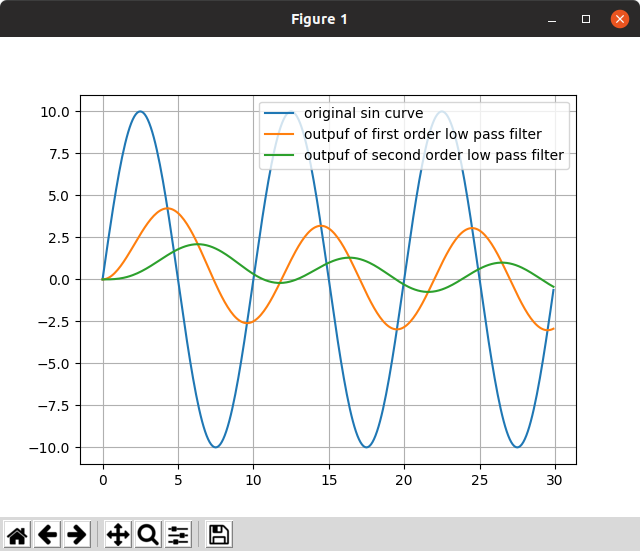
plt.plot(time_list, sin_curve, label="original sin curve")
plt.plot(T_first, y_first, label="outpuf of first order low pass filter")
plt.plot(T_second, y_second, label="outpuf of second order low pass filter")
plt.grid()
plt.legend()
plt.show()

ここで気づいたが，

• sinカーブの周波数$f$ = 1 ÷ sinカーブの周期$T$ = sinカーブの角周波数$\omega$ ÷ $2\pi$

である一方で，ローパスフィルタの時定数の$T$とカットオフ周波数$f$は

• カットオフ周波数$f$ = 1 ÷ （2$\pi$ * 時定数$T$）= カットオフ角周波数$\omega$ ÷（2$\pi$）

という関係がある．
このように，文脈によって時間に関する変数$T$の扱い方が異なるみたい．

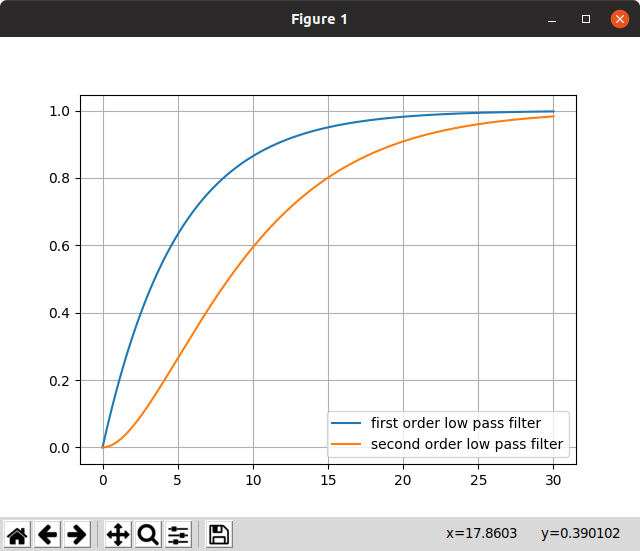
また，ステップ応答時の挙動の違いとして，初速が0になるという特徴がある．もっというと，速度が$t=0$の前後で連続になる．

#!/usr/bin/env python3
import control
import control.matlab
from matplotlib import pyplot as plt
import numpy

time_constant = 5.0
natural_freq = 1 / time_constant
damping_ratio = 1.0
G_first = control.tf([0, 1], [time_constant, 1])
G_second = control.tf([0, 0, natural_freq**2], [1, 2 * damping_ratio * natural_freq, natural_freq**2])

time_list = numpy.arange(0, 30, 0.001)
(y_first, T_first) = control.matlab.step(G_first, T=time_list)
(y_second, T_second) = control.matlab.step(G_second, T=time_list)

plt.plot(T_first, y_first, label="first order low pass filter")
plt.plot(T_second, y_second, label="second order low pass filter")
plt.grid()
plt.legend()
plt.show()

次に，時間領域で考える．ステップ応答をラプラス変換すると$\frac{1}{s}$なので，ローパスフィルタ後の出力を周波数領域で表すと（簡単のため減衰比$\zeta = 1$とする）

\frac{\omega_n^2}{s^2 + 2 \omega_n s + \omega_n^2}\frac{1}{s} = \frac{1}{s} - \frac{1}{s + \omega_n} - \frac{\omega_n}{\left(s + \omega_n\right)^2}

となる．
これを逆ラプラス変換すると

y(t) = 1 - \left(1 + \omega_n t\right)\mathrm{e}^{-\omega_n t}

となる．
これを微分して$t=0$を代入してみると，初速が0であることが分かる．

PD制御について

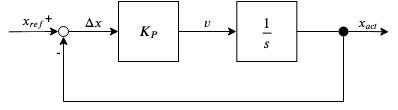
まず，以下のようなブロック線図を考える．$P(s)$は対象とするプラントの伝達関数であり，$C(s)$は適用したコントローラの伝達関数である．また，$r$は目標値，$e$は目標値と現在値の誤差，$u$はプラントに対する制御入力，$x$は現在値である．時間領域の表現を小文字，周波数領域の表現を大文字で表す．

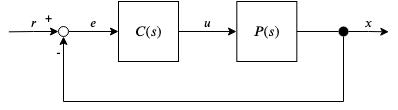
つまり

\begin{align}
X(s) &= P(s) U(s)\\
U(s) &= C(s) E(s)\\
e &= r - x
\end{align}

という関係性を持つブロック線図を考える．
このブロック線図を書いた人がやりたいことは，どんな目標値$r$を与えたとしても現在値$x$がなる早で$r$に収束させることになる．$X(s) = R(s)$と常に完全一致すればみんな幸せだし，$P(s)$が既知なら可能であるが，一般に未知なので完全一致は無理で，収束していく感じで妥協する．

ここで，$X(s) = G(s) R(s) \Leftrightarrow \frac{X(s)}{R(s)} = G(s)$の$G(s)$を閉ループ伝達関数と呼ぶ．この$G(s)$は目標値$r$に対する現在値$x$の応答を表しており，この$G(s)$だけをフィーチャーして考えればシステムの安定性などの重要な特性を議論でるので人気となっている．
で，変数除去をすると閉ループ伝達関数は

G(s) = \frac{P(s) C(s)}{1 + P(s) C(s)}

となる．

P制御

速度を積分すると位置になるという関係性をプラントとみなし，現在の位置を目標の位置に近づけるP制御を考えると，以下のブロック線図になる．

このときの閉ループ伝達関数は

G(s) = \frac{X_{act}}{X_{ref}} = \frac{\frac{K_P}{s}}{1 + \frac{K_P}{s}} = \frac{1}{1 + \frac{1}{K_P}s}

となる．これは，一次のローパスフィルタと同じ形であることが分かる！
なので，P制御で位置制御をすると，一次のローパスフィルタに対してステップ入力をしたときの挙動になる．

PD制御

加速度を２回積分すると位置になるという関係性をプラントとみなし，現在の位置を目標位置に近づけるPD制御を考えると，以下のブロック線図になる．

時間領域で書くと

\ddot{x} \leftarrow K_D \left(\dot{x}_{ref} - \dot{x}_{act}\right) + K_P \left(x_{ref} - x_{act}\right)

このときの閉ループ伝達関数は

G(s) = \frac{X_{act}}{X_{ref}} = \frac{K_D s + K_P}{s^2 + K_D s + K_P}

となる．

ここで，目標速度を0にすると，つまり，

として，

\ddot{x} \leftarrow K_D \left(0 - \dot{x}_{act}\right) + K_P \left(x_{ref} - x_{act}\right)

とすると，閉ループ伝達関数は

G(s) = \frac{X_{act}}{X_{ref}} = \frac{K_P}{s^2 + K_D s + K_P}

となる．

これは二次のローパスフィルタと同じ形であることが分かる！
なので，PD制御で位置制御をして，かつ，速度目標値に0を使うとすると，ニ次のローパスフィルタに対してステップ入力をしたときの挙動になる．

#!/usr/bin/env python3
import control
import control.matlab
from matplotlib import pyplot as plt
import numpy

time_constant = 5.0
natural_freq = 1 / time_constant
damping_ratio = 1.0
G_P = control.tf([0, 1], [time_constant, 1])
G_PD = control.tf([0, 2 * damping_ratio * natural_freq, natural_freq**2], [1, 2 * damping_ratio * natural_freq, natural_freq**2])
G_PD2 = control.tf([0, 0, natural_freq**2], [1, 2 * damping_ratio * natural_freq, natural_freq**2])

time_list = numpy.arange(0, 30, 0.1)
sin_one_cycle = 10.0
sin_omega = 1 / sin_one_cycle
sin_curve = 10 * numpy.sin(2 * numpy.pi * sin_omega * time_list)

(y_P, T_P, _) = control.matlab.lsim(G_P, U=sin_curve, T=time_list)
(y_PD, T_PD, _) = control.matlab.lsim(G_PD, U=sin_curve, T=time_list)
(y_PD2, T_PD2, _) = control.matlab.lsim(G_PD2, U=sin_curve, T=time_list)

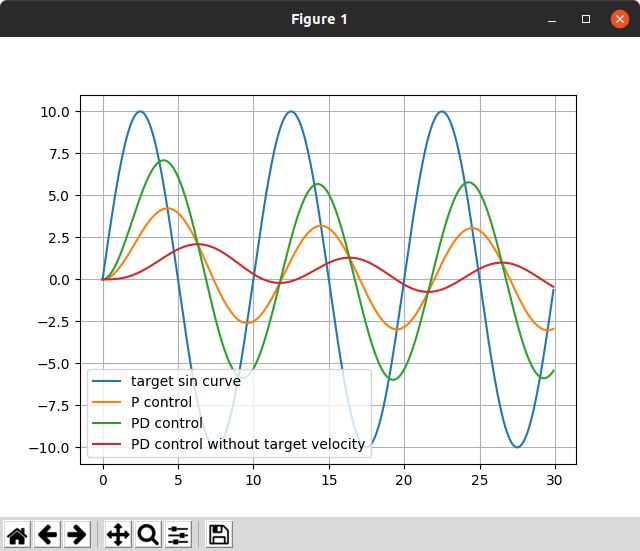
plt.plot(time_list, sin_curve, label="target sin curve")
plt.plot(T_P, y_P, label="P control")
plt.plot(T_PD, y_PD, label="PD control ")
plt.plot(T_PD2, y_PD2, label="PD control without target velocity")
plt.grid()
plt.legend()
plt.show()

このように，目標値追従性能はPD制御が最も良さそうということが分かる．

#!/usr/bin/env python3
import control
import control.matlab
from matplotlib import pyplot as plt
import numpy

time_constant = 5.0
natural_freq = 1 / time_constant
damping_ratio = 1.0
G_P = control.tf([0, 1], [time_constant, 1])
G_PD = control.tf([0, 2 * damping_ratio * natural_freq, natural_freq**2], [1, 2 * damping_ratio * natural_freq, natural_freq**2])
G_PD2 = control.tf([0, 0, natural_freq**2], [1, 2 * damping_ratio * natural_freq, natural_freq**2])

time_list = numpy.arange(0, 30, 0.001)
(y_P, T_P) = control.matlab.step(G_P, T=time_list)
(y_PD, T_PD) = control.matlab.step(G_PD, T=time_list)
(y_PD2, T_PD2) = control.matlab.step(G_PD2, T=time_list)

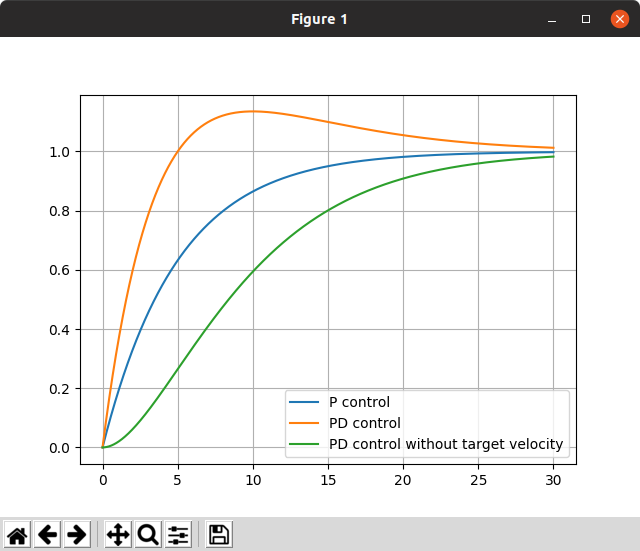
plt.plot(T_P, y_P, label="P control")
plt.plot(T_PD, y_PD, label="PD control")
plt.plot(T_PD2, y_PD2, label="PD control without target velocity")
plt.grid()
plt.legend()
plt.show()

一方で，ステップ応答への追従性能はこのようになる．PD制御だとオーバーシュートする．

アドミッタンス制御（位置制御型インピーダンス制御）

位置制御型のロボットでは接触力を制御するためのアドミッタンス制御という制御がある．実装例としてはhrpsys-baseのインピーダンス制御がある．
これはエンドエフェクタの位置$x$を

M \left(\ddot{x}_{ref} - \ddot{x}\right) + D \left(\dot{x}_{ref} - \dot{x}\right) + K \left(x_{ref} - x\right) = f_{ref} - f_{act}

という運動方程式に従うように求めることで，$f_{act}$が$f_{ref}$に収束することを目指す制御である．
これは

\frac{X_{ref} - X_{act}}{F_{ref} - F_{act}} = \frac{1}{K}\frac{K}{M s^2 + D s + K} = \frac{1}{K}\frac{\frac{K}{M}}{s^2 + \frac{D}{M} s + \frac{K}{M}}

のように二次遅れローパスフィルタと同じ形をしている．

例えばバルブに手を伸ばそうとしているときは$f_{ref}=0$となっていて，バルブが思ったより手前にあったとすると$f_{act}$が入ってきて，それが二次遅れで目標位置に伝わって，$x_{act}$は$x_{ref}$から収束することになる．ただ，$f_{act}$は0にはならない．つまり，目標力を実現することはなく，メリットは過度な$f_{act}$を出さないことにある．
また，バルブに接触している状態で接触力を発生させたい場合は，$f_{ref}=5N$で$f_{act}=0N$だったとすると，$5 / K[m]$だけ動いて止まる．そのときに$f_{act}$が何Nになるのかは状況次第．

まとめ

• P制御は一次のローパスフィルタと等価
• 速度目標値無視型PD制御は二次のローパスフィルタと等価
• trackingするという行為と急峻な変化をなますという行為は等価ではない