ASEとQuantum Espressoを使って、Ptが単純立方構造、fcc、hpcのいずれの構造をとるかを調べる

はじめに

　Jupyter上で、PythonライブラリであるASE(Atomic Simulation Environment)を介して、第一原理計算ソフトQuantum Espressoで、第一原理計算を実施してみます。
　本記事は、書籍『密度半関数理論入門(D.S.ショール，J.A.ステッケル 著、佐々木泰造，末原茂 共訳』(以下、教科書)の例題や課題を参考に、プログラムを作って計算します。

　なお、固体DFTの専門家ではありませんので、計算条件、結果等はご自身でご確認/判断ください。

今回は、教科書2章の練習問題１、
『Ptが単純立方構造・fcc・hpcのいずれの構造をとるかをDFTから見積もる』
問題に取り組んでみたいと思います。

前準備

計算に必要になるライブラリや、擬ポテンシャルを用意します。

*.jpynb

# import libs
import os
import subprocess
import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit

# import ase
from ase.build import bulk
from ase.visualize import view
from ase.calculators.espresso import Espresso

#Cuの例にならい、Ptのpw91の擬ポテンシャルを使います。
!wget http://nninc.cnf.cornell.edu/psp_files/Pt.pw91-n-van.UPF
pp_file="Pt.pw91-n-van.UPF"

関数の定義

計算するための構造を作る関数、計算条件を設定する関数などを作ります。今回は結晶系や格子定数a,cを変量するので、それに対応した関数を作ります。

*.ipynb

def make_crystal_lattice(type=None, a=None,c=None):
    model = bulk(name='Pt', crystalstructure=type, a=a, c=c,orthorhombic=False, cubic=False, basis=None)
    return model

def calc_dft_pt():
    pseudopotentials = {'Pt':pp_file}
    cmd = 'mpirun -np 5 pw.x -in espresso.pwi > espresso.pwo'
    input_data = {
        'control':{'pseudo_dir':'./'},
        'system': {
            'occupations' : 'smearing',
            'smearing' : 'mp',
            'degauss' : 0.001,
            'ecutwfc': 25.0,     #25[Ry] ~ 340[eV]
            'ecutrho': 100.0},   #ecutwfc * 4
        'disk_io': 'low'}

    calc = Espresso(command=cmd,
                    pseudopotentials=pseudopotentials,
                    kpts=(12, 12, 12),
                    input_data=input_data)
    return calc

def move_results_file(dir_for_result):
    # QEの計算ファイルを別のフォルダにまとめて格納する
    os.makedirs(dir_for_result, exist_ok=True)
    subprocess.call('mv espresso.* pwscf.save pwscf.xml '+dir_for_result+'/.', shell=True)
    subprocess.call('cp *.UPF '+dir_for_result+'/.', shell=True)

結晶系と格子定数を変えてDFT計算

まずは単純立方格子(sc)で格子定数aを変量してエネルギーを計算します。

*.ipynb

l_type = 'sc'
a_list = np.arange(2.5, 3.05, 0.05)
r=[]
for lat_a in a_list:
    print(f" a :{lat_a:.2f} [Angs.]")
    Pt = make_crystal_lattice(type=l_type, a=lat_a)
    Pt.set_calculator(calc_dft_pt())
    r.append(Pt.get_potential_energy()/len(Pt))
    move_results_file(l_type+"/a"+'{:.2f}'.format(lat_a))

a_sc = np.array(a_list)
r_sc = np.array(r)

###実行結果###
 a :2.50 [Angs.]
 a :2.55 [Angs.]
 ....

続いて面心立方格子fcc、六方最密構造hcpで格子定数を変えて計算します。hcpの方は、aとc/aを変量してエネルギーを計算します。計算数が多いこともあり、少し時間がかかります。できればcalc_dft_pt()内、cmdの-npの数字をPCのCPUコア数まで上げて計算してください。

*.ipynb

# fcc
l_type = 'fcc'
a_list = np.arange(3.75, 4.3, 0.05)

r=[]
for lat_a in a_list:
    print(f" a :{lat_a:.2f} [Angs.]")
    Pt = make_crystal_lattice(type=l_type, a=lat_a)
    Pt.set_calculator(calc_dft_pt())
    r.append(Pt.get_potential_energy()/len(Pt))
    move_results_file(l_type+"/a"+'{:.2f}'.format(lat_a))

a_fcc = np.array(a_list)
r_fcc = np.array(r)

#hcp
l_type = 'hcp'
c_per_a_list = np.arange(1.6, 1.85, 0.05)  # For hcp #0.05
a_list = np.arange(2.5, 3.5, 0.05)

r_hcp=[]
for c_per_a in c_per_a_list :
    r=[] 
    for lat_a in a_list :
        print(f" c/a:{c_per_a:.2f}, a :{lat_a:.2f} [Angs.]")
        Pt = make_crystal_lattice(type='hcp', a=lat_a, c=c_per_a*lat_a) # For hcp
        Pt.set_calculator(calc_dft_pt())
        r.append(Pt.get_potential_energy()/len(Pt))
        fname=f'{l_type}/ca{c_per_a:.2f}_a{lat_a:.2f}'
        move_results_file(fname)
    r_hcp.append(r)

ca_hcp = np.array(c_per_a_list)
a_hcp = np.array(a_list)
r_hcp = np.array(r_hcp)

計算結果の解析

まずは、格子定数に対するエネルギー変化を見てみましょう。

*.ipynb

# make a fig.
plt.rcParams["font.size"] = 12
fig = plt.figure(figsize=(5,4))
plt.xlabel("a [Angstrom]")
plt.ylabel("Etot/atom [eV]")
plt.plot(a_sc,r_sc,label="sc")
plt.plot(a_fcc,r_fcc,label="fcc")
for i, ca in enumerate(c_per_a_list):
    plt.plot(a_hcp, r_hcp[i],label=f'hcp_ca{ca:.1f}')
plt.ylim(-1212.1,-1211.0)
plt.legend(fontsize=8)
plt.show()
fig.savefig("result.png")

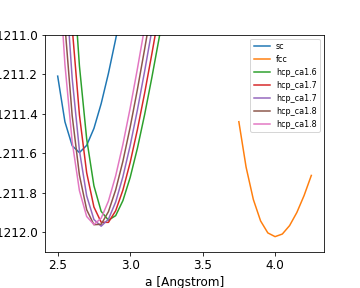
図 sc,fcc,hcpにおけるPtの格子定数aに対する全エネルギーEtot(a)

fccが若干エネルギーが低そうです。念のためそれぞれの構造のエネルギー最小値を確認してみましょう。

*.ipynb

print(f'Emin(sc ) = {r_sc.min():.2f}')
print(f'Emin(fcc) = {r_fcc.min():.2f}')
print(f'Emin(hcp) = {r_hcp.min():.2f}')
print("----")
print(f'lattice_a @ Emin(fcc) = {a_fcc[r_fcc.argmin()]:.2f}')

###実行結果###
Emin(sc ) = -1211.60
Emin(fcc) = -1212.02
Emin(hcp) = -1211.97
----
lattice_a @ Emin(fcc) = 4.00

fccが最もエネルギーが低く、最適化された格子定数は4Åであることがわかります。
この値は、今回変量したaの中で最もエネルギーが低かったaということになります。
ここで、fccのDFT結果に、Birch Murnagham状態方程式にFittigしてa0と平衡体積弾性率B0を求めてみます。

*.ipynb

def Birch_Murnagham_EoS(a, a0, B0, B02, E0):
    #a:lattice_a
    E = 9*(a**3)/4*B0/16 * ( B02*( (a0/a)**2-1)**3 + ( ((a0/a)**2-1)**2 * (6-4*(a0/a)**2) ) ) +E0
    return E

print('Fit Birch Murnagham EoS')
init_param = np.array([4, 142, 0, 0]) #初期値与えないとうまく収束しない
fit_params, std = curve_fit(Birch_Murnagham_EoS, a_fcc, r_fcc, p0=init_param, maxfev=10000)
est_BMeos = Birch_Murnagham_EoS(a_fcc, *fit_params)
print(f' a0 = {fit_params[0]:.2f}  [Angstrom]')
print(f' B0 = {fit_params[1]* 160.21766208:.2f}  [GPa]')

###実行結果###
Fit Birch Murnagham EoS
 a0 = 4.00  [Angstrom]
 B0 = 244.71  [GPa]

a0 = 4.00 [Angstrom]、B0 = 244.71 [GPa]という結果。

実験値との比較

下記に他の資料からの値を掲載します。

• Crystal Structure: fcc (Spece Group : Fm-3m)　　^[Ref.1]
• Lattice Constant : 3.925 [Angstrom]　　^[Ref.1]
• Bulk modulus : 230[GPa]　　^[Ref.2]
  Ref.1 : Ebert H. et al, Z. Phys. Chem. v.144,p.223, (1985) by NIMS AtomWorks
  Ref.2 : Wikipedia(実験値?)

DFTで求められた構造と格子定数はよく一致しているかと。B₀は５％以上異なっていますがこんなものなんでしょうか....

---

ASEとQuantum Espresso関連の投稿記事リンク

ASEとQuantum Espressoを使って、

• 手動でCuの単位格子最適化して、平衡体積弾性率を見積る
• Ptが単純立方構造、fcc、hpcのいずれの構造をとるかを調べる
• 六方晶Hfの格子定数aとcを最適化する
• H2Oなどの３原子分子を構造を最適化して、安定構造を見つける

他

• ASEでモデルの図を保存する,描写する,モデルを出力する(png,cif,traj,pov)
• Quantum Espressoを色々なライブラリでコンパイルして、自分のPCに最速な状態にする