概要
今回はフラクタルブラウン運動(Fractal brown motion(FBM))と、それを応用したドメインワープについて調べたのでそれについて書きたいと思います。
ちなみにドメインワープってなんぞや、というところですが以下の動画のような絵を描ける方法です。

上記の動画は、Shadertoyのデモで実際に動くものが見れます。
要は、こうした雲や波のような表現を計算によって(ノイズによって)表現しよう、というものです。
なお、今回の記事は以下の記事を参考にさせていただいています。
上記記事でもドメインワーピングについて触れられていますが、大本はInigo Quilez氏のこちらの記事です↓
フラクタルブラウン運動とは
表題のひとつの「フラクタルブラウン運動」とはなんでしょうか。
「フラクタル」の名前からなんとなく想像つくかもしれませんが、いわゆるフラクタル図形に代表される「自己相似性」のある図をノイズによって生み出すもの、と解釈しています。
フラクタルブラウン運動のベースはノイズ
フラクタルブラウン運動の説明の前にノイズの話を。
フラクタルブラウン運動はノイズによって生み出されます。
ノイズは以下のような感じのザラザラした絵ですね。
上記のようなノイズはプログラムから生成することができます。(ノイズ関数)
ポイントはノイズ関数を「オクターブを変えて重ねる」
フラクタルブラウン運動は前述の「ノイズ関数」を複数回重ねることで実現するものです。
そしてその重ね方にも特徴があります。
参考にさせていただいた記事から引用すると以下のように記されています。
周波数を一定の割合で増加させる(lacunarity)と同時に振幅を減らしながら(gain)ノイズを(octaveの数だけ)繰り返し重ねることで、より粒度の細かいディテールを持ったノイズを作り出すことができます。このテクニックは「非整数ブラウン運動(fBM)」または単に「フラクタルノイズ」と呼ばれていて、最も単純な形は下記のコードのようになります。
大事な点は「周波数を一定の割合で増加させる(lacunarity)と同時に振幅を減らしながら(gain)ノイズを(octaveの数だけ)繰り返し重ねる」という点です。
さらにこの「octave(オクターブ)の数だけ」繰り返すというのがポイントで、オクターブをWikipediaで調べると以下のように記されています。
オクターヴは、西洋音楽における8度音程であり、周波数比2:1の音程である。
周波数比2:1の音程、というのがポイントですね。
なので大体の実装では、指定した回数(オクターブ)分、forループで繰り返し処理させ、周波数をループのたびに2倍にしていく、という実装が多く見られます。
コード断片で示すと以下のような感じです。
# define OCTAVES 5
float fbm(vec2 p)
{
float result = 0.0;
float amplitude = 1.0;
for (int i = 0; i < OCTAVES; i++)
{
result += amplitude * noise(p);
amplitude *= 0.5;
p *= 2.0;
}
return result;
}
コード解説の前にもう一度説明を引用すると、
周波数を一定の割合で増加させる(lacunarity)と同時に振幅を減らしながら(gain)ノイズを(octaveの数だけ)繰り返し
ここで、周波数に対応するのがpです。(今回のサンプルは2次元の画像なのでたんにUV座標です)
そしてamplitudeが「振幅」ですね。
つまり、周波数をループごとに2倍にしながら、振幅を0.5倍(減少)し、OCTAVES分繰り返しているわけです。
この2.0や0.5はサンプルでは固定値となっていますが、実装によっては変数化して動的に変えられるようにしているケースもあります。
とはいえ大事な点は、「ループごとに周波数を増幅させ、振幅を減少させる」です。
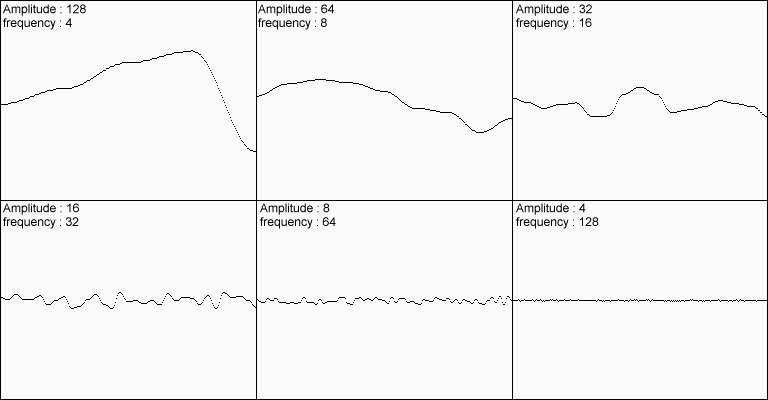
こちらの記事(パーリンノイズを理解する | POSTD)でもオクターブについて言及されており、その画像を引用させていただくと以下のような感じになります。
図で見るとオクターブごとの周波数と振幅の変化が分かりやすいですね。
図を見てもらうと分かりますが、Amplitudeが半分になり、frequencyが倍になっていっているのが分かりますね。
そしてそれぞれの振幅、周波数をグラフ化したものを見ると、「徐々に細かく」なっていっているのが分かるかと思います。
つまり、この大小の波を合成することでフラクタル特有の「自己相似性」を生み出している、というわけなんですね。
(拡大しても縮小しても似た波の形状が現れる)
ノイズ関数は任意
フラクタルブラウン運動については以上です。
これを実現するのに利用するノイズは任意のノイズ関数で良さそうです。
(冒頭の動画は以下のようにとてもシンプルなノイズ関数で表現したものです)
// Get random value
float random(in vec2 st)
{
return fract(sin(dot(st.xy, vec2(12.9898, 78.233))) * 43758.5453123);
}
// Get noise
float noise(in vec2 st)
{
// Splited integer and float values.
vec2 i = floor(st);
vec2 f = fract(st);
float a = random(i + vec2(0.0, 0.0));
float b = random(i + vec2(1.0, 0.0));
float c = random(i + vec2(0.0, 1.0));
float d = random(i + vec2(1.0, 1.0));
// -2.0f^3 + 3.0f^2
vec2 u = f * f * (3.0 - 2.0 * f);
return mix(a, b, u.x) + (c - a) * u.y * (1.0 - u.x) + (d - b) * u.x * u.y;
}
余談ですが、以前にパーリンノイズについて記事を書いたので、パーリンノイズに興味がある方は読んでみてください。
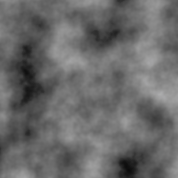
パーリンノイズがどんなものかというと、以下の画像のような「雲模様」を描くことができるノイズです。(こちらの画像もフラクタルブラウン運動を使っています)
ドメインワーピング
一番書きたかったのはこの「ドメインワーピング」です。
ドメインワーピング自体はInigo Quilez氏のこちらの記事が詳細に説明されています。
これを応用すると、以下のようなすばらしい映像を描き出すこともできます。
(これはレイマーチングと呼ばれる方法で、GLSLのプログラムコードだけで実現している映像です)

https://www.shadertoy.com/view/4sXGRM
レイマーチングの仕組みについては以前、Qiitaに記事を書いているので、興味がある方はそちらも合わせてご覧ください。
[2018.10.18追記]
上記のとは若干違う作品ですが、Shadertoyでも人気の以下の作品のコードリーディングについて記事に書きました。
ドメインワーピングの仕組み
大雑把に説明すると、FBM(Fractal Brownian Motionの略)関数の引数をFBM関数自身によって歪め、それを利用することで冒頭の動画のような効果を得る、というものです。
冒頭のものはFBM関数に渡す引数を時間によって徐々に変化させることで動きを出しています。
まずは実装したコードを見てみましょう。
(冒頭のShadertoyで利用しているコードを若干変更し、より簡易的なものにしています)
void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
// 解像度から、UV座標に変換(正規化)
vec2 st = fragCoord / iResolution.xy;
vec3 color = vec3(0, 0.745, 0.9);
// 最初の引数
vec2 q = vec2(0.0);
q.x = fbm(st + vec2(0.0));
q.y = fbm(st + vec2(1.0));
// 最初の引数をさらに加工。
// 1.7, 9.2などの数字は任意の数字。特別な意味はなし。
vec2 r = vec2(0.0);
r.x = fbm(st + (4.0 * q) + vec2(1.7, 9.2) + (0.15 * iTime));
r.y = fbm(st + (4.0 * q) + vec2(8.3, 2.8) + (0.12 * iTime));
// やっていることは以下と同義
// d1とd2は便宜上設定した追加パラメータ(上の例ではvec2(1.7, 9.2)などがそれ。
// fbm(st + fbm(st + fbm(st + d1) + d2))
// つまり、3段階のfbmで最後の係数を求めている
float f = fbm(st + 4.0 * r);
// f^3 + 0.6f^2 + 0.5f
float coef = (f * f * f + (0.6 * f * f) + (0.5 * f));
color *= coef;
fragColor = vec4(color, 1.0);
}
上記は、Shadertoyで利用されるメイン関数の中身です。
コメントにも書いていますが、途中で出てくるvec2(1.7, 9.2)などの数字は特に意味のある数字ではありません。
ランダム性を変化させる目的で使っていて、任意の数字を指定することができます。
(Shadertoyではコードを変更して実行できるので、色々数字を変化させて見てみると分かるかと思います)
肝は複数回のfbm関数による引数の加工
コード量もそれほど多くないので処理を追うのはそれほど大変ではないと思います。
今回のドメインワーピングを理解するにあたって重要な点は、fbm関数の引数をfbm関数自身で微妙に変化させながら最終的なアウトプットとする点です。
コメントにも書いてある通り、定数などを除去して数式風に変換すると以下のようになります。
\begin{eqnarray}
f &=& fbm(st + fbm(st + fbm(st + d_1) + d_2)) \\
result &=& f^3 + 0.6f^2 + 0.5f
\end{eqnarray}
やっていることはとてもシンプルですね。
定義したfbm関数の引数に、微妙に異なる値を加算したものを引数とし、その戻り値をさらにfbm関数に渡し・・・というのを3回繰り返しています。
(この繰り返し回数は任意のようです。実際、2回だけにしても似たアニメーションとなりました)
実際のところ、ノイズによって歪んだ空間を、さらに同じノイズで歪ませるため似たような変化が連続して起き、結果的に流体のようなアニメーションになるのだと思います。
ちなみに最後の方に出てくる3次関数ですが、これをグラフにすると以下のようななめらかな曲線になります。
(ただ、この3次関数による補間を行わなくてもアニメーションなどには影響ないようでした)
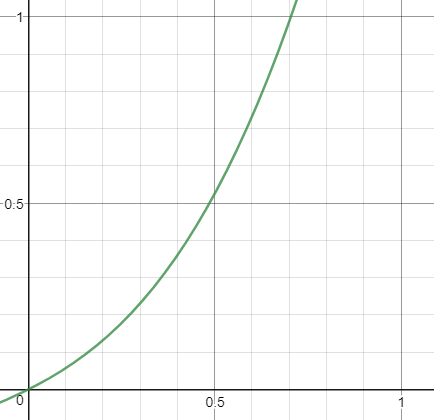
https://www.desmos.com/calculator/klxrt5nslu
コード全文
最後に、今回Shadertoyに投稿したシェーダコード全文を載せておきます。
(元のコードは、今回の記事の参考にさせてもらった記事(非整数ブラウン運動)から引用させていただき、必要最低限の状態に変更した上でコメントを追加したものとなります)
/**
* Fractal Brownian Motion
*
* Reference: https://thebookofshaders.com/13/
*
* See also: http://www.iquilezles.org/www/articles/morenoise/morenoise.htm
* : http://www.iquilezles.org/www/articles/warp/warp.htm
*/
const vec3 mixColor1 = vec3(0.8, 0.35, 0.12);
const vec3 mixColor2 = vec3(0.3, 0.75, 0.69);
# define NUM_OCTAVES 5
// Get random value
float random(in vec2 st)
{
return fract(sin(dot(st.xy, vec2(12.9898, 78.233))) * 43758.5453123);
}
// Get noise
float noise(in vec2 st)
{
// Splited integer and float values.
vec2 i = floor(st);
vec2 f = fract(st);
float a = random(i + vec2(0.0, 0.0));
float b = random(i + vec2(1.0, 0.0));
float c = random(i + vec2(0.0, 1.0));
float d = random(i + vec2(1.0, 1.0));
// -2.0f^3 + 3.0f^2
vec2 u = f * f * (3.0 - 2.0 * f);
return mix(a, b, u.x) + (c - a) * u.y * (1.0 - u.x) + (d - b) * u.x * u.y;
}
// fractional brown motion
//
// Reduce amplitude multiplied by 0.5, and frequency multiplied by 2.
float fbm(in vec2 st)
{
float v = 0.0;
float a = 0.5;
for (int i = 0; i < NUM_OCTAVES; i++)
{
v += a * noise(st);
st = st * 2.0;
a *= 0.5;
}
return v;
}
void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
// Calculate normalized UV values.
vec2 st = fragCoord / iResolution.xy;
vec3 color = vec3(0.0);
vec2 q = vec2(0.0);
q.x = fbm(st + vec2(0.0));
q.y = fbm(st + vec2(1.0));
// These numbers(such as 1.7, 9.2, etc.) are not special meaning.
vec2 r = vec2(0.0);
r.x = fbm(st + (4.0 * q) + vec2(1.7, 9.2) + (0.15 * iTime));
r.y = fbm(st + (4.0 * q) + vec2(8.3, 2.8) + (0.12 * iTime));
// Mixed color by 'q' and 'r'.
color = mix(color, mixColor1, clamp(length(q), 0.0, 1.0));
color = mix(color, mixColor2, clamp(length(r), 0.0, 1.0));
// Calculate by 'r' is that getting domain warping.
float f = fbm(st + 4.0 * r);
// f^3 + 0.6f^2 + 0.5f
float coef = (f * f * f + (0.6 * f * f) + (0.5 * f));
color *= coef;
fragColor = vec4(color, 1.0);
}