この記事は「GLSL Advent Calendar 2016」の 17日目 の記事になります。
前日までdoxasさんの独壇場でとても高度な内容だったのに、その後にこの記事をアップするのはとても気が引けましたが勇気を出してアップしますw
概要
そろそろレイトレーシングに挑戦する時期かなということで、レイトレの一種である「レイマーチング」について再入門してみたいと思います。(前に少しだけやって放置してた)
※ ちょっと長くなりそうなので、今回の記事はvol.1としました。
レイトレとは
レイトレ(レイトレーシング)とは、Wikipediaを引用させてもらうと以下のような意味になります。
レイトレーシング(ray tracing)は、波の線(伝播経路)を追跡することで、ある点において観測される画像・音像などをシミュレートする計算手法である。
レイトレーシングを行う対象は「光線」が基本でありこれは「光線追跡法」とも呼ばれるが、他にも「電波」「地震波」「超音波」などでも行われることがあり、それぞれ「波線追跡法」「音線追跡法」などと呼ばれることもある。
ある点(ある人の視点・耳・電波観測装置など)に届く光線・波線(電波の仮想的な線)・音線(音波の仮想的な線)などを逆にたどることによって、その点における視像(画像)・音像などを描画する。たとえば光線であれば、物体の表面の反射率、また透明度・屈折率等々を細かく反映させた像を得られるのが特徴で、1画素ずつ光線の経路を計算するので、高い画質で描画することができるという特長がある、が反面、一般的に計算量は多くなる。
この手法では反射や屈折は忠実に再現できるが、回折は近似やモデリングを必要とする。対象が異なっても伝播経路を追跡する基本的な原則は共通であるが、計算手順はそれぞれで異なる。
ざっくり言うと、「視点に入ってくる光の経路を追跡(トレース)する」ということです。
人間は目で物を見ます。そして周りの物が見えるのは、その物体が反射している光を視神経で電気信号に変換して、それを脳に届け、脳がそれを解釈しているからです。
つまり、人間は光を電気信号に変えて世界を認識している、というわけですね。
そしてレイトレーシングはまさにこの「光」の経路を細かに追跡することによって、視神経に届くはずの光を計算から導き出そう、というものです。
(実際にはカメラのレンズに入る光をイメージしたほうが分かりやすいかもしれませんが)
完全に余談ですが、レイトレで通常「トレースする」と言った場合、「視点から光源への経路」を追跡することを指します。
一方、「光源から視点への経路」の場合、「逆トレース」となります。感覚からすると逆ですが、元々は「視点からの光の経路」を求めることが先に作られたためにそうなっています。
レイマーチングとは
さて、レイマーチングとはなんでしょうか。レイマーチングはレイトレの一種です。
光(レイ)を行進(マーチ)させてトレースする手法のため、レイマーチング、と呼ばれています。
ざっくりとフローを挙げると、
- カメラ(視点)の方向を決める
- (1)の方向にレイを飛ばす
- シーン内のオブジェクト すべて と当たり判定を行い、「現在の位置」から一番近いオブジェクトへの距離を求める(※1、※2)
- (3)で求めた距離分だけ、レイの位置を進める
- (3)に戻り、オブジェクトとの距離がしきい値を超えた、あるいは規定回数の計算が終わったら終了
という流れになります。
・・フローだけ見てもなんのこっちゃ、ですねw
※1 ... 当たり判定のチェックは、ある程度の絞込などで軽減することが可能です。が、今回の記事では登場オブジェクトが少ないので総当りで書いています。
※2 ... 「現在の位置」とは、初期位置はカメラの位置になります。そこからレイを行進(マーチ)させ、「現在位置」を行進していきます。
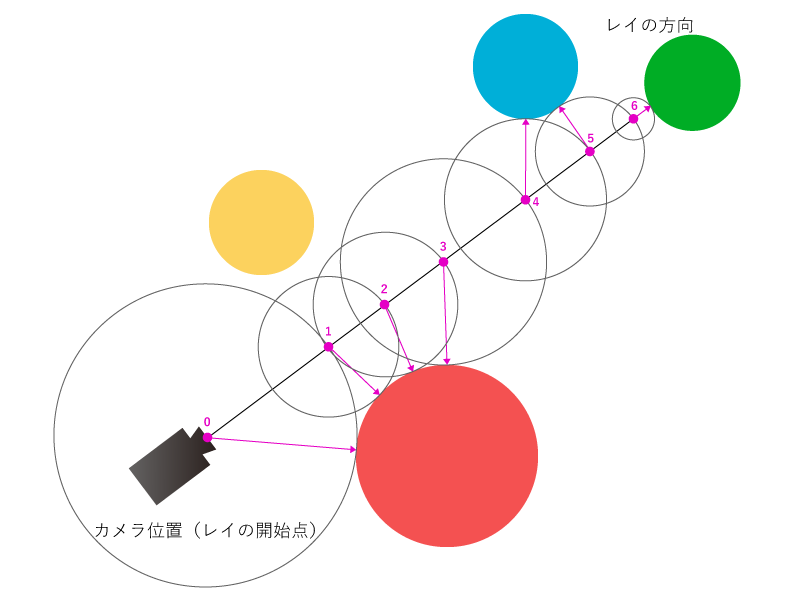
以下にレイマーチのイメージを載せておきます。
ぱっと見はちょっとなにが行われているのか分かりづらいかもしれませんが、ひとつずつ見ていけば難しいことはありません。
注目してほしいところは紫色の点と矢印です。
図中の数字は何回目のレイの位置計算か、を表しています。計算回数を重ねるごとに、カメラの視点方向にある緑色の球体に近づいていっているのが分かると思います。
では順番に見ていきましょう。
まず、最初の位置(カメラの位置)から一番近いオブジェクトの「距離」を求め、視点方向にその分だけ進めます。(紫色の0番がカメラの視点位置になっているのが分かるかと思います。)
(このとき、あくまで「一番近いオブジェクトへの距離」は「カメラの視点方向とはまったく関係なく」、総当りで全オブジェクト表面への直線距離を求め、その中から最も短いものを選択しているに過ぎません。これを間違えて「視点方向に一番近いオブジェクト」と考えてしまうと理解がむずかしくなってしまうので注意が必要です)
計算してみると、カメラの視点位置から一番近いオブジェクトは赤の球体というのが分かります。
そしてその赤い球体までの距離を表しているのが、0番から伸びている紫色の矢印です。
ただし、矢印はあくまで「球体への距離を利用するのみ」で方向は関係ありません。
そして0番から伸びている紫色の矢印の同心円状に1番の点があります。
視点位置から、赤い球体への距離分レイを進めるとちょうどその位置になりますよね。
続けて同じ計算を行います。すると、今度も赤い球体が一番近い距離になりました。
同じようにレイを進め、さらに次の計算を行います。
すると今度は、レイが赤い球体を行き過ぎていますが依然として赤い球体が一番近いオブジェクトです。
さらにレイを進めてみましょう。
すると、4番目の位置にきた時点でやっと、今度は青い球体が一番近いオブジェクトになりました。
5番目も同様ですね。
そして6番目の位置にきたときにやっと、緑色のオブジェクトが一番近いオブジェクトとなりました。
緑色のオブジェクトは実際にレイが当たっているオブジェクトになるため、ここで計算は終了し、レイは緑色のオブジェクトにぶつかった、ということで緑色を検知したことになります。
以上が、簡単なレイマーチの動作の仕組みです。
こんな感じで、とにかく視点位置からレイを飛ばしまくって、ぶつかったオブジェクトの色を見つけてそれをレンダリングしていくのがレイトレでのレンダリング手法となります。
実装解説
さて、文章だけでは眠くなってきてしまうかもしれないので、以後はコードを交えつつ説明していきたいと思います。
ちなみに解説するコードを実行すると、以下のような形になります。
どうでしょうか。
サンプルはとてもシンプルに「球体」をレンダリングしています。
(サンプルはGLSL Sandboxで実際に動作しているところを見ることができます。 http://glslsandbox.com/e#37221.1 )
このあとに解説しますが、とあるオブジェクトの形状を描き出す関数として「距離関数」というものがすでにいくつも求められています。
これらを応用することで、(そして組み合わせることで)様々な形状を描き出すことが可能となります。
一枚のプレーンにドットを打つイメージ
実装解説に入る前にひとつだけ。
今回のサンプル(というか、レイトレや様々なポストエフェクトなど)はポリゴンを利用していません。
代わりに、一枚のプレーンにドットを打っていくような感じでレンダリングしていきます。
今回のサンプルを理解するのに地味に重要なので覚えておいてください。
(1枚のキャンバスにレイを飛ばして色を決定していく、というのをイメージすると分かりやすいかもしれません)
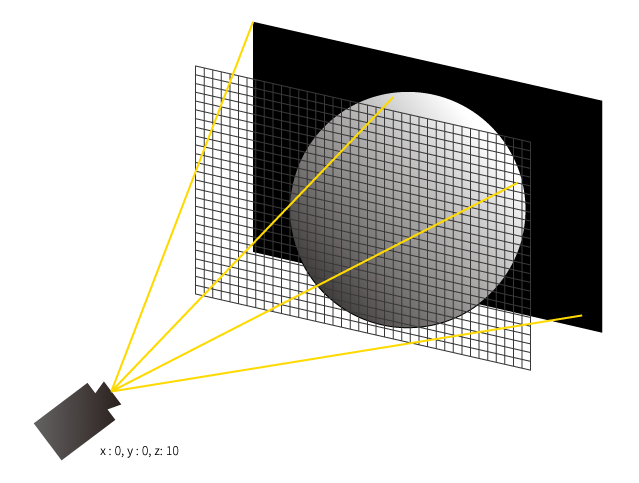
(格子になっているところがドットです。ドットひとつひとつにレイを飛ばして、そこの色を決定していく、というイメージです)
全体のコードを見てみる
まずは今回のサンプルのコード全体を見てみたいと思います。(前述したGLSL Sandboxのものです)
コード自体は長くないのでさらっと見てみてください。
# ifdef GL_ES
precision mediump float;
# endif
# extension GL_OES_standard_derivatives : enable
uniform float time;
uniform vec2 mouse;
uniform vec2 resolution;
vec3 lightDir = normalize(vec3(1.0, 1.0, 1.0));
float dist_func(vec3 pos, float size)
{
return length(pos) - size;
}
vec3 getNormal(vec3 pos, float size)
{
float ep = 0.0001;
return normalize(vec3(
dist_func(pos, size) - dist_func(vec3(pos.x - ep, pos.y, pos.z), size),
dist_func(pos, size) - dist_func(vec3(pos.x, pos.y - ep, pos.z), size),
dist_func(pos, size) - dist_func(vec3(pos.x, pos.y, pos.z - ep), size)
));
}
void main( void )
{
// 解像度からテクスチャとして利用できる`-1~1`の間に正規化する
vec2 pos = (gl_FragCoord.xy * 2.0 - resolution.xy) / min(resolution.x, resolution.y);
vec3 col = vec3(0.0);
vec3 cameraPos = vec3(0.0, 0.0, 10.0);
vec3 ray = normalize(vec3(pos, 0.0) - cameraPos);
vec3 cur = cameraPos;
vec2 mouseNorm = mouse * 2.0 - 1.0;
float size = 1.0 - length(mouseNorm);
for (int i = 0; i < 16; i++)
{
float d = dist_func(cur, size);
if (d < 0.0001)
{
vec3 normal = getNormal(cur, size);
float diff = dot(normal, lightDir);
col = vec3(diff) + vec3(0.1);
break;
}
cur += ray * d;
}
gl_FragColor = vec4(col, 1.0);
}
読みやすいように改行を多めに入れているので長く見えますが、実際はそんなに長いコードではありません。
GLSLを多少書いたことがある人であればそれほどむずかしいと感じないと思います。
では、順を追ってひとつずつ見ていきましょう。
コードの最初のほうでいくつかの関数が定義されていますが、まずはmain関数の中から見ていきます。
解像度を正規化する
まずは以下のコードを見てください。
// 解像度からテクスチャとして利用できる`-1~1`の間に正規化する
vec2 pos = (gl_FragCoord.xy * 2.0 - resolution.xy) / min(resolution.x, resolution.y);
通常、GLSLで扱う値は基本的に1.0以下の値になります。
なので、解像度をそのまま使うととんでもなく大きな数字になってしまうため、それを正規化して扱いやすいようにしているのが上記の計算です。
gl_FragCoordには計算中のピクセルの位置がシステムから渡されます。
これは解像度と同じ範囲のため、当然ながら1.0以上の値が渡されてきます。(フルHDなら1920×1080ですね)
しかしこのままだと、前述のように適切に値を扱うことができません。
そこで、GLSL Sandboxでは解像度の値を渡してくれています。それがresolutionという変数です。
この値で割ることによって、解像度の値が0.0~1.0の間の値に正規化できる、というわけです。
ただ話はこれだけで終わらなくて、今回のサンプルでは、0.0~1.0の範囲ではなく、-1.0~1.0の範囲に正規化してやる必要があります。
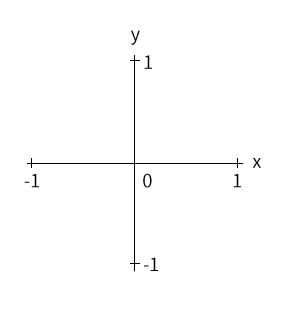
(下の図のように、数学でよく見るグラフをイメージしてもらうと分かりやすいと思いますが、中心から左はマイナスになっていますよね)
この-1.0~1.0の間に補正しているのが上記の計算の意味になります。
これをさらに、縦横の解像度の値のうち、小さいほうで割っているのは画角を保つためです。
これを行わないと横に間延びした画像になってしまいます。(ためしにサンプルを変更してもらうと分かると思います)
この正規化は、wgld.orgさんのレイトレ話など、様々なところで必要になってくるので、このコード断片を見たら「あ、正規化してるんだな」って思えるようになっておくと色々と捗ります。
レイを定義する
続いてレイの定義を見てみます。
vec3 cameraPos = vec3(0.0, 0.0, 10.0);
vec3 ray = normalize(vec3(pos, 0.0) - cameraPos);
vec3 cur = cameraPos;
上の図で、カメラの位置からまっすぐにレイを飛ばしていたのを思い出してください。
ここで行っている処理は、あの図のようにレイを飛ばすための準備です。
まず最初に行っているのは「カメラの位置」を定義しています。
このあたりは任意の数値です。カメラをもっと近づけたければZの値を小さくすればいいし、少し上からの視点にするならYの値を大きくすればOKです。
続くrayの定義は、「レイの方向」を定義している箇所です。
レイの定義のイメージは上で紹介した以下の図のようになります。
カメラの位置から、スクリーンの各ドットに対してレイを飛ばしています。
格子状の部分がドットのイメージです。
これを全ピクセル分行うわけですね。
普通のモニタであっても相当な数のレイを飛ばす必要があることが容易に想像できます。
最近では4Kのディスプレイも当たり前になってきていますし、今後ますます、画面に向かって飛ばすレイの数が増えていくことでしょう。
余談ですが、これをCPUでやっていては、当然ですが処理が追いつきません。
しかしGPUの場合は全ドットに対して「同時に」計算を行う、優れた並列処理があるために、高速に計算が行えているわけなんですね。
前に、CPUとGPUを「ひとりの天才と100人の凡人」と例えて分かりやすい!と言ってもらえたのでここでも書いておきますw
閑話休題。
さて、最後の部分は
vec3 cur = cameraPos;
ですが、これはカメラの位置をレイの初期位置としています。
冒頭のレイマーチのイメージ図で言うと、0番目の位置を指定したことになります。
以後は、前述のように、各オブジェクトごとの距離を計算し、一番近いオブジェクトの距離分だけレイを進めていくことになります。
レイを進める
for (int i = 0; i < 16; i++)
{
float d = dist_func(cur, size);
if (d < 0.0001)
{
vec3 normal = getNormal(cur, size);
float diff = dot(normal, lightDir);
col = vec3(diff) + vec3(0.1);
break;
}
cur += ray * d;
}
さていよいよ大詰めです。
最後の部分は「レイを進める処理」です。
レイマーチの名の通り、for文を使って徐々にレイの位置を進めているのが分かるかと思います。
dist_funcは「距離関数」です。距離関数に関しては後述しますが、ざっくり言うと「オブジェクトへの最短距離を計算する関数」です。
前述のように、レイの位置から一番近いオブジェクトへの距離分、レイを進めていく仕組みのため、この距離関数が使われているわけですね。
さて、d < 0.0001はなにを意味しているかと言うと。
一言で言うと「レイがオブジェクトに限りなく近づいた」ことを表現しています。
(dは距離(distance)の意味と捉えてください)
もしこのif文の中に入らないとすると、まだレイはどのオブジェクトともぶつかっていないことになります。
そのため、if文のブロックをスキップしてcur += ray * dを実行しています。
これがまさに、「レイの位置」を「レイの方向」に「一番近いオブジェクトの距離分」進めている箇所になります。
さて、ではなにかしらのオブジェクトにレイが当たった場合はどういう処理をしているのでしょうか。
具体的には以下の部分です。
vec3 normal = getNormal(cur, size);
float diff = dot(normal, lightDir);
col = vec3(diff) + vec3(0.1);
getNormal関数は距離関数とともに説明しますが、「法線を得ている」というのは伝わるかと思います。
続く行は、たんにディレクショナルライトの位置を定義したベクトルと内積を取って、光の辺り方(強度)を計算しているだけです。
あとはその強度と若干のAmbientLight風の色を乗せて、最終的な色の決定を行っています。
この値を画面に出力してやれば、サンプルのような球体が描かれる、というわけですね。
とってもシンプル!
距離関数で表される様々な図形
さて、以上でレイマーチによる球体のレンダリングについての解説は終わりです。
球体を描くだけならこれだけのコードで描くことができます。
が、やはり球体を描くだけでは色々なものを表現しきれません。
それ以外の形状はどう描いたらいいのでしょうか。
その答えは「こちらのサイト」にあります。
サイトを見てもらうと分かりますが、実に様々な図形が、とてもシンプルな数式で表せているのが分かるかと思います。
ひとつ具体例を上げましょう。
Boxのレンダリング
Boxのレンダリングは以下のようになります。

(サンプル用にコード書いたので貼っておきます。 http://glslsandbox.com/e#37410.0 )
コード
距離関数のコードはこんな感じです↓
float udBox( vec3 p, vec3 b )
{
return length(max(abs(p) - b,0.0));
}
球体に負けないくらいシンプルです。
ただ、若干なにをしているのかが分かりづらいですね。
自分も最初見たときは「なんでこんな計算でBoxがレンダリングできるんだヨ!」って思いました。
色々考えて、そういうことかーと腑に落ちたので、それを残しておきたいと思います。なにかの参考になれば幸いです。
Boxの距離関数の理解
一言で言うと、Boxの表面へ垂線を引くイメージです。
いくつかのレイの位置とBoxサイズで計算してみるとイメージができてくるかもしれません。
マイナス位置にあるレイは強制的にプラスの空間に移動させられる
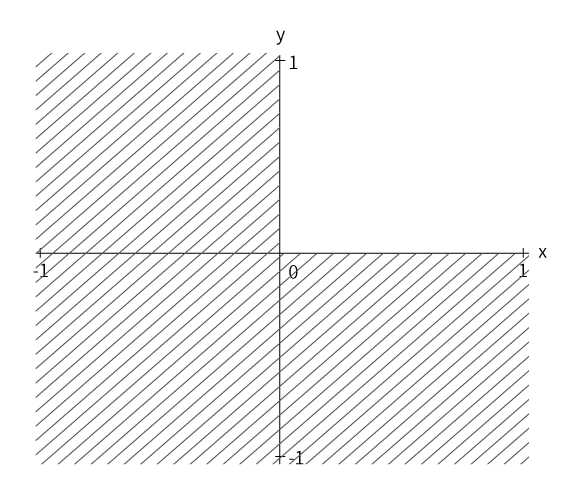
まずは以下の図を見てみてください。
斜線で表された部分はグラフ的には X,Y いずれかがマイナスのエリアです。
なぜこの図を書いたかと言うと。
距離関数を見てみると、レイの位置をabs関数によってすべてがプラスに転じて計算されます。
つまりすべての値がプラスに転じる、というわけですね。
そしてそれを図示したのが上図というわけです。
これ、地味に大事です。
つまり、レイの位置がどこにあろうと、図の斜線が引かれていないエリア(右上のエリア)の範囲ですべてを考えることができるわけです。
これでだいぶ計算が単純化されますね。
しかしなせそうするのでしょうか。
結局のところ、Boxが原点に置かれていると考えると、どの位置にレイがあっても、上図の斜線がないエリアで計算を行うのと相対的には変わらないからに他なりません。
なので、単純化するために絶対値を取って計算しているというわけなんですね。
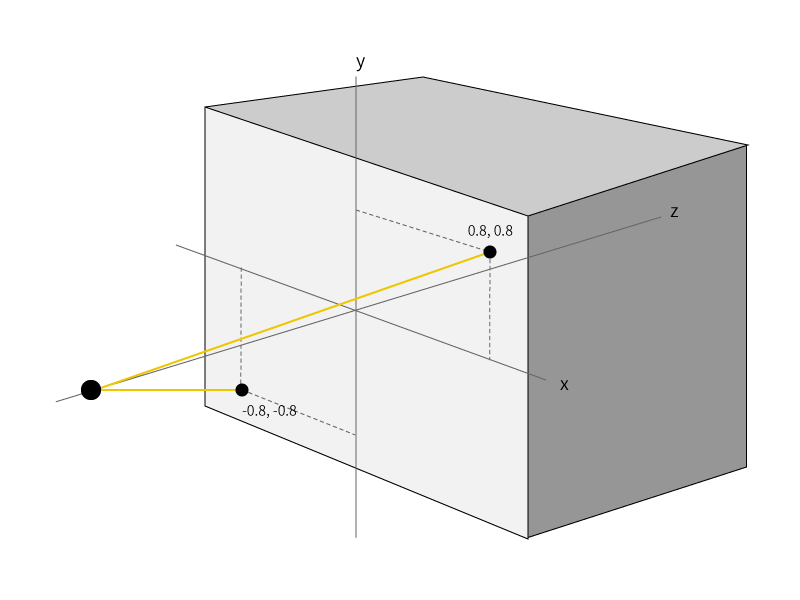
ちょっと分かりづらいかもしれませんが、(0.8, 0.8)の位置に向かうレイと、(-0.8, -0.8)に向かうレイは距離は同じになりますよね。
なので、プラス側だけの計算でも問題ない、というわけです。
差分ベクトルはBoxの表面へのベクトルに補正される
さて、プラスエリアで考えることで計算が単純化されました。
あとはそのエリアの中でBoxとの距離計算、つまり「最短距離」が計算できればいいわけです。
そしてその計算の大事なポイントはmax関数で0以下の場合はすべて0として扱う点です。
でもそれはなぜでしょうか。
想像してみてください。
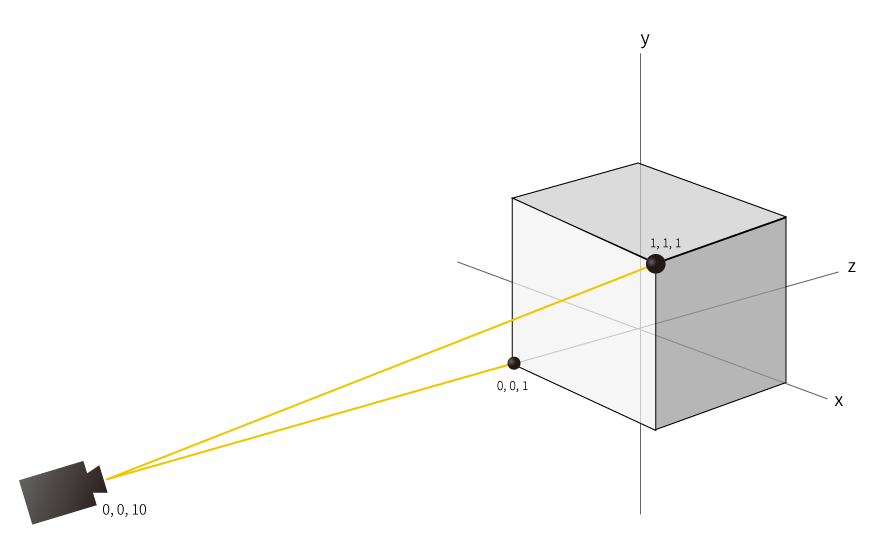
Boxのサイズが(1, 1, 1)で、レイの位置が(0, 0, 10)、レイの方向が(0, 0, -1)だとします。
図にすると以下になります。
さて、距離関数を見てみると、レイの位置の絶対値からBoxのサイズを引いています。
例ではBoxのサイズは(1, 1, 1)としました。これをそのまま座標と考えると、Box内にあるひとつの頂点の座標と見ることができます。
Boxのサイズを座標ベクトルとして使い、レイの位置とのベクトル計算と考えると、「Boxの頂点(1, 1, 1)からレイの位置への位置のベクトル」と考えられます。(差分ベクトル)
差分ベクトルということは、ある頂点から別のある頂点への方向と距離を持ったベクトルになります。つまり距離が求まった、というわけですね。
しかし図を見てみると最短距離にはなっていないことに気づくと思います。
図の通りであれば、レイの位置の正面に位置する点が最短距離となるはずですよね。
ポイントはmax関数
距離関数をあらためて見てみると、max関数が使われているのが分かります。
まずはなにをしているかを置いておいて、実際に距離関数によって計算をしてみましょう。
abs(0, 0, 10) - (1, 1, 1) = (-1, -1, 9)
となります。xyzの各要素をそれぞれ計算しただけですね。
あれ? 計算結果にマイナスがありますね。
計算結果はmax関数によって調整されるため、最終的な計算結果は(0, 0, 9)となります。
答えが見えてきました。
(1, 1, 1)頂点への計算だったはずが、マイナスが取り払われたため、レイの位置から正面に位置する頂点への距離に結果が変わりました。
(実際に、レイの方向に9だけ進めると(0, 0, 1)となって、Boxの頂点と重なります)
これがmax関数を利用したカラクリです。
ひとつずつ考えてみると単純ですね。
Boxの外側のレイは強制的にBoxの正面に移動される
上記のmax関数は実際のところ、なにをしていたのでしょうか。
それは、レイがBox(厳密には頂点(例では(1, 1, 1)の点))の正面から、マイナス方向に外れた位置にあった場合に、強制的に正面へ移動させていたと見ることができます。
もう少し具体的に言うと。
Boxの頂点に自分が移動し、レイを見つめていると想像してみてください。
そして、そこからレイの位置を見ると(上の図をベースに考えると)やや右下のほうに見えるはずです。
それが(-1, -1, 9)という計算結果ですね。その方向にレイの位置があります。
さてこのレイへのベクトルを頂点の正面に持ってくるにはどうしたらいいか。
正面、ということはX, Y軸ともに0になっていれば正面になりますね。
そうです。この処理をしているのがmax関数の役割です。
なので、Boxの正面から外にある位置のレイに関してはどれもが正常に計算されていた、というわけです。
一方、レイの位置が、頂点から見て左側に存在する場合はどうなるでしょうか。
その場合はmax関数による補正がかかりません。(計算結果がマイナスにならないからですね)
ちょっと言葉では説明しづらいのですが、前述の「正面に持ってくる」処理が必要なのは、減算に利用している(1, 1, 1)という数値は、原点から一番遠い位置にある頂点の位置でした。
そして、レイが右下にあるということは、この「一番遠い位置の頂点」よりも近くになる頂点が存在していることになります。
なので、そのまま距離計算としてしまうと「最短距離」の計算になりません。
しかし、「一番遠い頂点」から見て左側にレイの位置がある場合は、「レイから見て一番近い点は、原点から一番遠い頂点」になりますよね。
つまり、なにも補正をかけなくても、その頂点への距離を計算してやれば「最短距離」となるわけです。
ものすごく大雑把に言うと、Boxの距離関数の計算は、計算に利用した頂点への最短距離を求めると、結果としてBox表面への最短距離を求めることと同義となる、というのが意味するところなのです。
・・・・と偉そうに書きましたが、実際の定義とかを調べたわけではなく、単純に計算式からどういうことをやったのかを想像しただけです。
なので間違ったことを書いているかもしれないのであくまで参考として考えてください。
(やっと説明書けた・・図にしてもなにしても、記事でこれを説明するのはしんどい( ;´Д`))
法線の取得
コードの解説ではさっと「法線を得ています」という簡単な解説で終わらせていましたが、実際のところ自分もまだ、なぜこの計算で法線が取得できるのかは分かっていません;
我無さん(@gam0022)のツイートを引用させてもらうと以下のようです。
距離関数の勾配は法線になるのを言葉で説明するの難しいよね
ほとんどの人は陽関数表現に慣れているから勾配とると傾きになるんじゃね?っと誤解してしまうし、距離関数=陰関数表現というところから説明しないといけない…
引用元: https://twitter.com/gam0022/status/804931136606478336
とのこと。
確かに微分すると(勾配)傾きになるイメージしかなかったのでなんで?となりますね。
と思って色々調べていたら、なぜそうなるかの解説動画があったので紹介しておきます。
動画の解説を見るに、陰関数のそれぞれの要素(X,Y)の微分を取り、その値とグラフの接線とのベクトルの内積を取ると0になる。
つまり、陰関数の微分したベクトルはグラフの接線と垂直である=法線ベクトルである、ということのようです。
何回か動画を見てイメージは湧きましたが、まだうまく説明できる自信がないので、興味がある人は動画を見てくださいw
コードの解説
さて、ではgetNormal関数がなにをしているか見てみましょう。
vec3 getNormal(vec3 pos, float size)
{
float ep = 0.0001;
return normalize(vec3(
dist_func(pos, size) - dist_func(vec3(pos.x - ep, pos.y, pos.z), size),
dist_func(pos, size) - dist_func(vec3(pos.x, pos.y - ep, pos.z), size),
dist_func(pos, size) - dist_func(vec3(pos.x, pos.y, pos.z - ep), size)
));
}
計、6回の距離関数の実行がされています。
そして引数に渡している値をよく見てみると、引いている側の距離関数(右側)の値は、x, y, zの要素がそれぞれ微量だけ引かれたものを利用しています。
微量だけ増減させた値、つまり微分を行っている、というわけですね。
そして前述の通り、距離関数(陰関数)を微分した結果は法線ベクトルとなるため、それを正規化して法線として利用している、というわけですね。
様々な距離関数(Distance Function)
今回紹介したのは球体とBoxの距離関数だけでしたが、それ以外にも様々な距離関数がすでに確立されています。
一番シンプルな球体から、かなり複雑な形状まで色々あります。
そしてそれらは以下のサイトでまとめられているので、どんなものがあるかを見てみるといいでしょう。
modeling with distance functions
今回解説した内容と、上記の距離関数を組み合わ合わせることで色々な形状を描き出すことができると思います。
次のvol.2ではこれら距離関数を組み合わせて複雑な形状を描く方法を書きたいと思います。