フラクタル地形自動生成

概要

マイクラなどの地形をどうやって自動生成しているのか気になったので，
代表的なものをさっくり実装して確認してみた．

この記事では，フラクタル地形についてさっくり紹介した後，以下の手法について述べる．
・バリューノイズ
・パーリンノイズ
・中点変位法

なお，全て二次元ベースで実装している．理論自体は何次元のものでも適用可能である．

事前準備

コード中でオレオレ構造体やオレオレマクロを使っているので，載せておく．

//指定範囲でクリップする.
#define CLIP(e,l,h) (min(max(e,l),h))

//配列の要素数取得.
#define COUNTOF(a) ( sizeof( a ) / sizeof( a[0] ) )

//ベクトル構造体.
#define VECTOR SVector2D<float>
template <class T>
struct SVector2D
{
    typedef T DataType;
    T x;
    T y;
    SVector2D(){ Init(); }
    void Init()
    {
        x = T();
        y = T();
    }
    SVector2D   operator +  ( const SVector2D& e ) const { SVector2D tmp; tmp.x = x + e.x; tmp.y = y + e.y; return tmp; }
    SVector2D&  operator += ( const SVector2D& e ){ x += e.x; y += e.y; return (*this); }
    SVector2D   operator -  ( const SVector2D& e ) const { SVector2D tmp; tmp.x = x - e.x; tmp.y = y - e.y; return tmp; }
    SVector2D&  operator -= ( const SVector2D& e ){ x -= e.x; y -= e.y; return (*this); }
    T           operator *  ( const SVector2D& e ) const { return ( x * e.x ) + ( y * e.y ); }
    SVector2D&  operator *= ( const int e ){ x *= e; y *= e; return (*this); }
    SVector2D&  operator *= ( const float e ){ x *= e; y *= e; return (*this); }
    SVector2D&  operator /= ( const int e ){ x /= e; y /= e; return (*this); }
    SVector2D&  operator /= ( const float e ){ x /= e; y /= e; return (*this); }
};

フラクタル地形とは

wikipedia曰く，
「フラクタル地形（フラクタルちけい、英: Fractal landscape）は、基本的には2次元形式のフラクタルによる海岸線であり、コッホ曲線の確率論的生成と見なすことができる。ハウスドルフ次元 D は、2 と 3 の間の小数である。」

なるほどよくわからん，ということでフラクタルのwikipediaを参照した所，
「フラクタル（仏: fractale, 英: fractal）は、フランスの数学者ブノワ・マンデルブロが導入した幾何学の概念である。図形の部分と全体が自己相似になっているものなどをいう。」
「フラクタルの具体的な例としては、海岸線の形などが挙げられる。一般的な図形は複雑に入り組んだ形状をしていても、拡大するに従ってその細部は変化が少なくなり、滑らかな形状になっていく。これに対して海岸線は、どれだけ拡大しても同じように複雑に入り組んだ形状が現れる。」

つまり，幾何学において，図形内の全体の形状と一部の形状が似通る性質を自己相似性と呼び，
そういった性質が現れている図形をフラクタル図形と呼んでいる，
そして，地形に自己相似性が現れているものをフラクタル地形と呼ぶってことらしい．
なお，海岸線の他に，雪の結晶やロマネスコなんかもフラクタルとして有名だが，
こちらは地形ではないので，フラクタル図形，フラクタル形状と呼ばれている．

バリューノイズ

概要

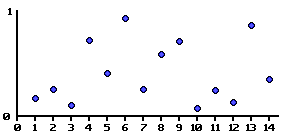
ホワイトノイズ(ただ乱数を羅列したノイズ)の乱数間を補間関数でボカしてあげたノイズ．
乱数間を補間することで，離散的な数値の羅列を波形に変換し，波形の連続性が自然な地形を再現する．
単純に乱数間を線形補間すると波形というよりは折れ線グラフになってしまうので，
五次関数などで補間することが多い．

　　　　　　　　↓↓↓

(引用：Perlinノイズの【ノイズ関数入門】)

これを二次元平面に適用する場合，1ピクセル単位で乱数を配置してしまうと，その間を補間することができない．
そのため，例えば8*8ピクセルを1ボックスとして，ボックス間で補間してあげるようにする．

コード

#define HASH_CODE_MAX       (256)
#define HASH_CODE_TABLE_NUM     (HASH_CODE_MAX*2)

int g_HashCode[ HASH_CODE_TABLE_NUM ] = {};

//乱数テーブル作成.
void SettingHash( unsigned int seed )
{
    //乱数ライブラリ初期化.
    srand( seed );

    //ハッシュコード初期化.
    memset( g_HashCode, 0, sizeof( unsigned int ) * COUNTOF( g_HashCode ) );

    //ランダムテーブル生成.
    const int TABLE_NUM = HASH_CODE_MAX;
    unsigned int randomTable[ TABLE_NUM ] = {};
    for( int i = 0; i < COUNTOF( randomTable ); ++i ){
        randomTable[i] = rand() % HASH_CODE_MAX;
    }

    //ハッシュコード生成.
    for( int i = 0; i < COUNTOF( g_HashCode ); ++i ){
        g_HashCode[i] = randomTable[i % TABLE_NUM];
    }
}

//乱数値取得.
unsigned int GetHash( int x, int y )
{ 
    x %= HASH_CODE_MAX; 
    y %= HASH_CODE_MAX; 
    return g_HashCode[ x + g_HashCode[y] ]; 
}

//乱数を0.0f~1.0fに正規化したものを取得する.
float GetValue( int x, int y )
{ 
    return (float)GetHash( x, y ) / (float)( HASH_CODE_MAX - 1 ); 
}

//五次補間関数.
float Fade( float t )
{ 
    //Ken Perlin氏(パーリンノイズを作った人)が考えだした補間関数.
    //6x^5 - 15x^4 + 10x^3.
    return ( 6 * powf( t, 5 ) - 15 * powf( t, 4 ) + 10 * powf( t, 3 ) ); 
}

//線形補間.
float Lerp( float a, float b, float t )
{ 
    return ( a + ( b - a ) * t ); 
}

//バリューノイズ取得.
float ValueNoise( float x, float y )
{
    //整数部と小数部に分ける.
    int xi = (int)floorf( x );
    int yi = (int)floorf( y );
    float xf = x - xi;
    float yf = y - yi;

    //格子点を取り出す.
    float a00 = GetValue( xi        , yi        );
    float a10 = GetValue( xi + 1    , yi        );
    float a01 = GetValue( xi        , yi + 1    );
    float a11 = GetValue( xi + 1    , yi + 1    );

    //小数部分を使ってそのまま線形補間してしまうと折れ線グラフになってしまうので.
    //線形補間する前に小数部分を五次補間関数で歪めちゃう.
    xf = Fade( xf );
    yf = Fade( yf );

    //位置を基準に，各格子点からの影響を考慮した値を算出する.
    return Lerp( Lerp( a00, a10, xf ), Lerp( a01, a11, xf ), yf );
}

//呼び出し例.
void Call()
{
    SettingHash(0);

    const float RECT_SIZE   = 32.0f;
    const int   COLOR_MAX   = 255;
    const int   IMAGE_SIZE  = 200;

    for( int i = 0; i < IMAGE_SIZE; ++i ){
        for( int j = 0; j < IMAGE_SIZE; ++j ){
            float x = (float)i / RECT_SIZE;
            float y = (float)j / RECT_SIZE;

            const int r = (int)((float)COLOR_MAX * ValueNoise( x, y ));
            const int g = (int)((float)COLOR_MAX * ValueNoise( x, y ));
            const int b = (int)((float)COLOR_MAX * ValueNoise( x, y ));

            //決まったRGBでピクセルを描画する的な.
            //SetPixel( image, i, j, RGB( r, g, b ) );
        }
    }
}

波形内の同じ頂点を参照しているのに参照する度に値が違う，といったことが起こらないように，
乱数をテーブルに保持している．

テーブルのサイズが乱数の最大値の2倍なのは，アクセスの利便性からである．
乱数テーブルから返ってくる値は，HASH_CODE_MAXが最大なので，
入力値をHASH_CODE_MAXでクリップさえしておけば，
g_HashCode[ x + g_HashCode[y] ]のようなアクセスの仕方でも，
最大値がHASH_CODE_MAX*2に収まるので，配列外アクセスなどのエラーチェックが必要ない．

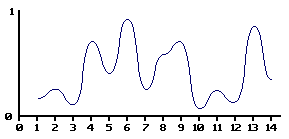
動作結果

補間はされているので，ホワイトノイズよりかは良いと思う．
が，フラクタルではない…ホワイトノイズ感も抜けてない…
とてもじゃないが使いものにならないので，オクターブという概念を導入してみる．

オクターブ

Perlinノイズの【Perlinノイズ関数を作成する】項曰く，
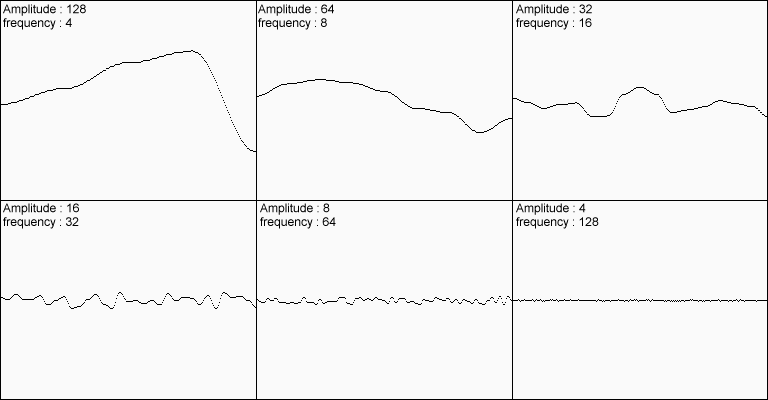
周波数と振幅が違う多様な波形を合成することで，小さい変化から大きな変化まで含んだ波形となり，より自然な形状となるんだそうな．確かにそんな気もしてくる．

　　　　　　↓↓↓

(引用：パーリンノイズを理解する)

その周波数と振幅を計算する数式としては以下が用いられる．

振幅 = persistence ^ i
周波数 = 2.0f ^ i

persistenceとは振幅を指定する数値で，マンデルブロがフラクタル発見後に命名したものである．
これが大きいと，その波形を合成した時の影響度が大きくなる．基本的には0.5fが使われる．
何故オクターブと呼ばれているのかというと，物理学におけるオクターブの定義が，特定の波形に対して周波数が二倍になるような波形のこと，となっているためである．
(上記の数式で周波数が2のべき乗になっていることに注目)

なお，ノイズの話やランダム地形生成 Part2～フラクタルブラウン運動にあるように，
フラクタルブラウン運動も同じような数式を示すらしい．
(物理学は門外漢なので何もわからないが，最終的に同じような結果が出るだけで，原理は違う気もする)

オクターブバリューノイズ

前述した通り，バリューノイズは波形であるため，オクターブは容易に適用できる．

コード

float OctaveValueNoise( float x, float y )
{
    float a = 1.0f;
    float f = 1.0f;
    float maxValue = 0.0f;
    float totalValue = 0.0f;
    float per = 0.5f;
    for( int i = 0; i < 5; ++i ){
        totalValue  += a * ValueNoise( x * f, y * f );
        maxValue    += a;
        a *= per;
        f *= 2.0f;
    }
    return totalValue / maxValue;
}

ValueNoise( x * f, y * f )について補足．
周波数を2倍にするというのは，波形の頂点数を2倍にするということと同義である．
今回の実装において頂点数を2倍にするには，関数呼び出し元に定義されているRECT_SIZEを0.5倍すればいい．
RECT_SIZEはいわば，頂点間の長さ，であるので，波形の長さが変わらない限り，
RECT_SIZEを大きくすれば波形内の頂点数は減るし，小さくすれば増える．

ValueNoise( x * f, y * f )は上記計算を以下のように式変形させただけである．

X / ( RECT_SIZE / 2.0f )    = x
X / RECT_SIZE               = x * 2.0f

動作確認

　

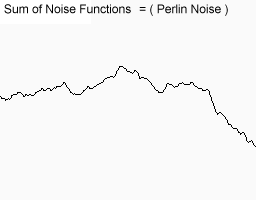
かなり綺麗になった．フラクタル感もある．
これなら実用に耐えそうではある．

パーリンノイズ

概要

Ken Perlin氏が，かの有名なディズニー映画「TRON」製作時に，より自然なテクスチャを得るべく考案されたとされるノイズ．
彼はこのノイズアルゴリズムでアカデミー賞を受賞したんだそうな．

基本的な処理内容はバリューノイズと変わらないが，波形の頂点が持っているものがちょっと違う．
バリューノイズでは，頂点が乱数値を持っていて，頂点からどれくらいの距離にいるか，をもとに頂点の値からノイズ値を決めていた．
パーリンノイズでは，頂点が勾配ベクトルを持っていて，頂点からどれくらいの距離，方向にいるか，をもとにノイズ値を決める．勾配ベクトル自体は乱数値から決定する．

実際にノイズ値を求める際には，各頂点が持っている勾配ベクトルと，
頂点から現在位置までの距離ベクトルを内積した結果をノイズ値とする．

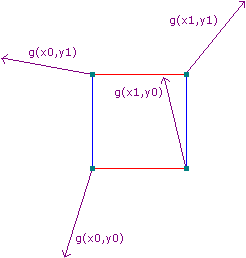
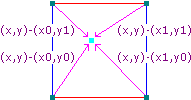
(左が各頂点の勾配ベクトル，右が各頂点から現在位置までの距離ベクトル)
(引用：パーリンノイズを理解する)

内積を取ることで，勾配ベクトルの方向にある地点は正の数値，つまり取りうる値の最大値に近づき，
逆方向にある地点は負の数値，つまり最低値に近づく．
なお，直交した場合と頂点自身は内積を取った結果が0になることに注意．

コード

float Grad( unsigned int hash, float a, float b )
{
    unsigned int key = hash % 0x4;
    switch( key )
    {
    case 0x0:   return a;   //a * 1.0f + b * 0.0f.
    case 0x1:   return -a;  //a * -1.0f + b * 0.0f.
    case 0x2:   return -b;  //a * 0.0f + b * -1.0f.
    case 0x3:   return b;   //a * 0.0f + b * 1.0f.
    };
    return 0.0f;
}

float PerlinNoise( float x, float y )
{
    //整数部と小数部に分ける.
    int xi = (int)floorf( x );
    int yi = (int)floorf( y );
    float xf = x - xi;
    float yf = y - yi;

    //格子点からハッシュを取り出し，その値を基に勾配を取得する.
    float a00 = Grad( GetHash( xi       , yi    ), xf       , yf        );
    float a10 = Grad( GetHash( xi + 1   , yi    ), xf - 1.0f, yf        );
    float a01 = Grad( GetHash( xi       , yi + 1), xf       , yf - 1.0f );
    float a11 = Grad( GetHash( xi + 1   , yi + 1), xf - 1.0f, yf - 1.0f );

    //補間をかける.
    xf = Fade( xf );
    yf = Fade( yf );

    //位置に合わせて格子点のどの点から一番影響を受けるかを決める.
    //(勾配関数内で内積を取っているので，ベクトルの向きによっては負の値が出る．範囲は-1.0f~1.0f).
    //(なので，正の値にするために1.0fを足して2.0fで割っている).
    return ( Lerp( Lerp( a00, a10, xf ), Lerp( a01, a11, xf ), yf ) + 1.0f ) / 2.0f;
}

勾配ベクトルは，正規ベクトル且つ矩形の中心地点から各辺に向かうようなベクトル，になっている．
理由はパーリンノイズを理解するを参照のこと．

動作結果

かなり自然な感じがする．しかもフラクタル感もある．
が，なんというか均一感が否めない．

オクターブパーリンノイズ

こちらにもオクターブを適用してみる．

コード

float OctavePerlinNoise( float x, float y )
{
    float a = 1.0f;
    float f = 1.0f;
    float maxValue = 0.0f;
    float totalValue = 0.0f;
    float per = 0.5f;
    for( int i = 0; i < 5; ++i ){
        totalValue  += a * PerlinNoise( x * f, y * f );
        maxValue    += a;
        a *= per;
        f *= 2.0f;
    }
    return totalValue / maxValue;
}

動作確認

かなり綺麗になった．フラクタル感も健在．
オクターブバリューノイズよりも若干平滑化されている感じだろうか．
煙とか雲とかのテクスチャになら全く違和感なく使える．

中点変位法

概要

wikipedia曰く
「正方形を4つの同じ大きさの小さい正方形に分割し、その中心の点を無作為な値で垂直方向に変位させる。この過程を4つに分けられた各正方形についても繰り返し、再帰的に実施して必要な詳細レベルに到達するまで行う。」

実装する際には，まず分割する前の領域の4頂点に対してランダムで値を決めた後，
中心の値を平均＋ランダムで決めて，更に矩形の各辺の中点の値も決める．
あとは同じことを分割しながら繰り返すだけである．

コード

#define TABLE_SIZE 200
int g_NoiseValue[ TABLE_SIZE ][ TABLE_SIZE ];

//テーブル生成.
void SetupMidpointDisplaceNoise( unsigned int seed )
{
    //乱数ライブラリ初期化.
    srand( seed );

    //ハッシュコード初期化.
    for( int i = 0; i < TABLE_SIZE; ++i ){
        for( int j = 0; j < TABLE_SIZE; ++j ){
            g_NoiseValue[i][j] = -1;
        }
    }

    //四隅に初期値を設定する.
    g_NoiseValue[0][0]                              = ( rand() % HASH_CODE_MAX );
    g_NoiseValue[TABLE_SIZE - 1][0]                 = ( rand() % HASH_CODE_MAX );
    g_NoiseValue[0][TABLE - 1]                  = ( rand() % HASH_CODE_MAX );
    g_NoiseValue[TABLE_SIZE - 1][TABLE_SIZE - 1]    = ( rand() % HASH_CODE_MAX );

    //残りの点を決定する.
    VECTOR topLeft; topLeft.x = topLeft.y = 0.0f;
    VECTOR rightBottom; rightBottom.x = rightBottom.y = (float)(TABLE_SIZE - 1);
    SetupMidpointDisplaceNoise( topLeft, rightBottom, HASH_CODE_MAX );
}

void Noise::SetupMidpointDisplaceNoise( VECTOR topLeft, VECTOR rightBottom, int heightMax )
{
    static const int    SMOOTH_COEF     = 4;

    //始点と終点の各成分.
    int nTop    = (int)floorf( topLeft.y );
    int nLeft   = (int)floorf( topLeft.x );
    int nBottom = (int)floorf( rightBottom.y );
    int nRight  = (int)floorf( rightBottom.x );

    //正方形の四点の値.
    const int nTopLeft      = g_NoiseValue[nLeft][nTop];
    const int nTopRight     = g_NoiseValue[nRight][nTop];
    const int nBottomLeft   = g_NoiseValue[nLeft][nBottom];
    const int nBottomRight  = g_NoiseValue[nRight][nBottom];

    //中点の位置.
    int nX  = (nLeft + nRight) / 2;
    int nY  = (nTop + nBottom) / 2;

    if( heightMax <= 1 ){
        int value = ( nTopLeft + nTopRight + nBottomLeft + nBottomRight ) / SMOOTH_COEF;
        value = CLIP( value, 0, HASH_CODE_MAX - 1 );
        if( g_NoiseValue[nX][nY] < 0 ){
            g_NoiseValue[nX][nY] = value;
        }
    }
    else{
        int value = ( nTopLeft + nTopRight + nBottomLeft + nBottomRight ) / SMOOTH_COEF;
        value += ( rand() % heightMax ) - ( heightMax / 2 );
        value = CLIP( value, 0, HASH_CODE_MAX - 1 );
        if( g_NoiseValue[nX][nY] < 0 ){
            g_NoiseValue[nX][nY] = value;
        }

        //上下左右の点も値を決める.
        {
            if( g_NoiseValue[nX][nTop] < 0 ){
                g_NoiseValue[nX][nTop]      = ( nTopLeft + nTopRight ) / 2;
            }
            if( g_NoiseValue[nX][nBottom] < 0 ){
                g_NoiseValue[nX][nBottom]   = ( nBottomLeft + nBottomRight ) / 2;
            }
            if( g_NoiseValue[nLeft][nY] < 0 ){
                g_NoiseValue[nLeft][nY]     = ( nTopLeft + nBottomLeft ) / 2;
            }
            if( g_NoiseValue[nRight][nY] < 0 ){
                g_NoiseValue[nRight][nY]    = ( nTopRight + nBottomRight ) / 2;
            }
        }

        //分割した正方形に関して，同じように中点の高さを決める.
        {
            VECTOR midPoint;        midPoint.x      = (float)nX;        midPoint.y      = (float)nY;
            VECTOR midUpEdge;       midUpEdge.x     = (float)nX;        midUpEdge.y     = (float)nTop;
            VECTOR midDownEdge;     midDownEdge.x   = (float)nX;        midDownEdge.y   = (float)nBottom;
            VECTOR midLeftEdge;     midLeftEdge.x   = (float)nLeft;     midLeftEdge.y   = (float)nY;
            VECTOR midRightEdge;    midRightEdge.x  = (float)nRight;    midRightEdge.y  = (float)nY;

            heightMax /= 2;
            SetupMidpointDisplaceNoise( topLeft,        midPoint,       heightMax );
            SetupMidpointDisplaceNoise( midUpEdge,      midRightEdge,   heightMax );
            SetupMidpointDisplaceNoise( midLeftEdge,    midDownEdge,    heightMax );
            SetupMidpointDisplaceNoise( midPoint,       rightBottom,    heightMax );
        }   
    }
}

float Noise::GetMidpointDisplaceNoise( float x, float y )
{
    int xi = (int)floorf( x );
    int yi = (int)floorf( y );
    return ( (float)g_NoiseValue[xi][yi] / (float)(HASH_CODE_MAX - 1) );
}

//呼び出し例.
void Call()
{
    SetupMidpointDisplaceNoise(0);

    for( int i = 0; i < TABLE_SIZE; ++i ){
        for( int j = 0; j < TABLE_SIZE; ++j ){
            float x = (float)i;
            float y = (float)j;
            const int r = (int)((float)COLOR_MAX * GetMidpointDisplaceNoise( x, y ));
            const int g = (int)((float)COLOR_MAX * GetMidpointDisplaceNoise( x, y ));
            const int b = (int)((float)COLOR_MAX * GetMidpointDisplaceNoise( x, y ));

            //取得したRGBでピクセルを描画する的な.
            //SetPixel( image, i, j, RGB( r, g, b ) );
        }
    }
}

動作結果

結構良い感じに出ていて，充分実用に耐えると思われる．フラクタル感もある．
が，所々で矩形が浮いて見えてしまっているのが，若干残念である．

参考

ノイズの話：各種ノイズの一覧と簡単な説明．分かりやすい．
パーリンノイズを理解する：パーリンノイズの実装を詳しく説明している．とても分かりやすい．
Perlinノイズ：パーリンノイズ関連の論文の和訳．が，元の論文の手法自体がパーリンノイズではなくバリューノイズであったため，パーリンノイズの説明足り得ていない．が，かなり分かりやすいしおすすめ．
ランダム地形生成 Part1～パーリンノイズ：パーリンノイズの解説記事．絵も入っていて分かりやすかった．が，若干読みづらい．
ランダム地形生成 Part2～フラクタルブラウン運動：フラクタルブラウン運動の解説記事．オクターブの話が若干混じっている気もするが，分かりやすい．
3Dグラフィックス・マニアックス　人工知性でコンテンツを生成するプロシージャル技術(4)：ゲーム業界で非常に有名な西川善司さんの解説記事．
次世代のスーパーエンジニアたちも学ぶ！マインクラフトで触れる技術たちその１:マインクラフト関連の記事一覧．分かりやすくまとめられている．

総括

色々手法がある中で，比較してみると以外と違いがあるものだなぁという印象．
状況に応じて使い分けたいものです．