概要
以前に、「[コードリーディング] レイマーチングによる波表現を読み解く」というタイトルで波表現をするレイマーチングのコードを読み解きました。
(そのときの動画はこれ↓)

今回はこちらのShadertoyの作品をコードリーディングしたいと思います。
ちなみにこんな感じの絵が出ます↓
(下記は、上の作品にコメントつけたり分かりやすくしたりしたもののキャプチャです)
こちらの作品を、自分が分かる範囲でコメントを付けつつ、変数などもできるだけ意味付けしながら解説・読解していこうと思います。
なお、自分がコメントを付けたバージョンはこちらにポストしてあります。
また読解に際して、こちらのブログ記事(Creating a Volumetric Ray Marcher)も参考にさせていただきました。
いちおう翻訳とかも全文やってみたのですが、書いた方が許可してくれたら掲載しようと思います。
許可されたので掲載しました。
コード全文
まずはコード全文を掲載します。
見てもらうと分かりますが、コード量はそれほど多くありません。
// ------------------------------------------
//
// This post cloned from "https://www.shadertoy.com/view/lss3zr"
//
// I also refer this blog post below.
// https://shaderbits.com/blog/creating-volumetric-ray-marcher
//
// This post is to learn how to cloud raymarching is working.
//
// ------------------------------------------
# define USE_LIGHT 0
mat3 m = mat3( 0.00, 0.80, 0.60,
-0.80, 0.36, -0.48,
-0.60, -0.48, 0.64);
float hash(float n)
{
return fract(sin(n) * 43758.5453);
}
///
/// Noise function
///
float noise(in vec3 x)
{
vec3 p = floor(x);
vec3 f = fract(x);
f = f * f * (3.0 - 2.0 * f);
float n = p.x + p.y * 57.0 + 113.0 * p.z;
float res = mix(mix(mix(hash(n + 0.0), hash(n + 1.0), f.x),
mix(hash(n + 57.0), hash(n + 58.0), f.x), f.y),
mix(mix(hash(n + 113.0), hash(n + 114.0), f.x),
mix(hash(n + 170.0), hash(n + 171.0), f.x), f.y), f.z);
return res;
}
///
/// Fractal Brownian motion.
///
/// Refer to:
/// EN: https://thebookofshaders.com/13/
/// JP: https://thebookofshaders.com/13/?lan=jp
///
float fbm(vec3 p)
{
float f;
f = 0.5000 * noise(p); p = m * p * 2.02;
f += 0.2500 * noise(p); p = m * p * 2.03;
f += 0.1250 * noise(p);
return f;
}
//////////////////////////////////////////////////
///
/// Like sphere distance function.
///
/// But this function return inverse value.
/// Normal dist function is like below.
///
/// return length(pos) - 0.1;
///
/// Because this function is used for density.
///
float scene(in vec3 pos)
{
return 0.1 - length(pos) * 0.05 + fbm(pos * 0.3);
}
///
/// Get normal of the cloud.
///
vec3 getNormal(in vec3 p)
{
const float e = 0.01;
return normalize(vec3(scene(vec3(p.x + e, p.y, p.z)) - scene(vec3(p.x - e, p.y, p.z)),
scene(vec3(p.x, p.y + e, p.z)) - scene(vec3(p.x, p.y - e, p.z)),
scene(vec3(p.x, p.y, p.z + e)) - scene(vec3(p.x, p.y, p.z - e))));
}
///
/// Create a camera pose control matrix.
///
mat3 camera(vec3 ro, vec3 ta)
{
vec3 cw = normalize(ta - ro);
vec3 cp = vec3(0.0, 1.0, 0.0);
vec3 cu = cross(cw, cp);
vec3 cv = cross(cu, cw);
return mat3(cu, cv, cw);
}
///
/// Main function.
///
void mainImage(out vec4 fragColor, in vec2 fragCoord)
{
vec2 uv = (fragCoord.xy * 2.0 - iResolution.xy) / min(iResolution.x, iResolution.y);
vec2 mo = vec2(iTime * 0.1, cos(iTime * 0.25) * 3.0);
// Camera
float camDist = 25.0;
// target
vec3 ta = vec3(0.0, 1.0, 0.0);
// Ray origin
//vec3 ori = vec3(sin(iTime) * camDist, 0, cos(iTime) * camDist);
vec3 ro = camDist * normalize(vec3(cos(2.75 - 3.0 * mo.x), 0.7 - 1.0 * (mo.y - 1.0), sin(2.75 - 3.0 * mo.x)));
float targetDepth = 1.3;
// Camera pose.
mat3 c = camera(ro, ta);
vec3 dir = c * normalize(vec3(uv, targetDepth));
// For raymarching const values.
const int sampleCount = 64;
const int sampleLightCount = 6;
const float eps = 0.01;
// Raymarching step settings.
float zMax = 40.0;
float zstep = zMax / float(sampleCount);
float zMaxl = 20.0;
float zstepl = zMaxl / float(sampleLightCount);
// Easy access to the ray origin
vec3 p = ro;
// Transmittance
float T = 1.0;
// Substantially transparency parameter.
float absorption = 100.0;
// Light Direction
vec3 sun_direction = normalize(vec3(1.0, 0.0, 0.0));
// Result of culcration
vec4 color = vec4(0.0);
for (int i = 0; i < sampleCount; i++)
{
// Using distance function for density.
// So the function not normal value.
// Please check it out on the function comment.
float density = scene(p);
// The density over 0.0 then start cloud ray marching.
// Why? because the function will return negative value normally.
// But if ray is into the cloud, the function will return positive value.
if (density > 0.0)
{
// Let's start cloud ray marching!
// why density sub by sampleCount?
// This mean integral for each sampling points.
float tmp = density / float(sampleCount);
T *= 1.0 - (tmp * absorption);
// Return if transmittance under 0.01.
// Because the ray is almost absorbed.
if (T <= 0.01)
{
break;
}
#if USE_LIGHT == 1
// Light scattering
// Transmittance for Light
float Tl = 1.0;
// Start light scattering with raymarching.
// Raymarching position for the light.
vec3 lp = p;
// Iteration of sampling light.
for (int j = 0; j < sampleLightCount; j++)
{
float densityLight = scene(lp);
// If densityLight is over 0.0, the ray is stil in the cloud.
if (densityLight > 0.0)
{
float tmpl = densityLight / float(sampleCount);
Tl *= 1.0 - (tmpl * absorption);
}
if (Tl <= 0.01)
{
break;
}
// Step to next position.
lp += sun_direction * zstepl;
}
#endif
// Add ambient + light scattering color
float opaity = 50.0;
float k = opaity * tmp * T;
vec4 cloudColor = vec4(1.0);
vec4 col1 = cloudColor * k;
#if USE_LIGHT == 1
float opacityl = 30.0;
float kl = opacityl * tmp * T * Tl;
vec4 lightColor = vec4(1.0, 0.7, 0.9, 1.0);
vec4 col2 = lightColor * kl;
#else
vec4 col2 = vec4(0.0);
#endif
color += col1 + col2;
}
p += dir * zstep;
}
vec3 bg = mix(vec3(0.3, 0.1, 0.8), vec3(0.7, 0.7, 1.0), 1.0 - (uv.y + 1.0) * 0.5);
color.rgb += bg;
fragColor = color;
}
さて、ではこれをベースにひとつずつ見ていきましょう。
ノイズ関数とFBM
冒頭で定義されている関数を見てみましょう。
mat3 m = mat3( 0.00, 0.80, 0.60,
-0.80, 0.36, -0.48,
-0.60, -0.48, 0.64);
float hash(float n)
{
return fract(sin(n) * 43758.5453);
}
///
/// Noise function
///
float noise(in vec3 x)
{
vec3 p = floor(x);
vec3 f = fract(x);
f = f * f * (3.0 - 2.0 * f);
float n = p.x + p.y * 57.0 + 113.0 * p.z;
float res = mix(mix(mix(hash(n + 0.0), hash(n + 1.0), f.x),
mix(hash(n + 57.0), hash(n + 58.0), f.x), f.y),
mix(mix(hash(n + 113.0), hash(n + 114.0), f.x),
mix(hash(n + 170.0), hash(n + 171.0), f.x), f.y), f.z);
return res;
}
///
/// Fractal Brownian motion.
///
/// Refer to:
/// EN: https://thebookofshaders.com/13/
/// JP: https://thebookofshaders.com/13/?lan=jp
///
float fbm(vec3 p)
{
float f;
f = 0.5000 * noise(p); p = m * p * 2.02;
f += 0.2500 * noise(p); p = m * p * 2.03;
f += 0.1250 * noise(p);
return f;
}
FBMで使われるオフセット行列
冒頭で定義されている行列(m)はおそらくオフセット行列でしょう。
ノイズに引数として与えられる点を少しずつ回転させる意味がありそうです。
実際に2x2行列にして点の移動を見てみると、適当にオフセットさせるような動きをします。
desmosで実際に点を動かしてみると、行列を適用した別の点がどう動くかを確認することができます。
 https://www.desmos.com/calculator/e0tlzb36sy
https://www.desmos.com/calculator/e0tlzb36sy
hash関数とnoise関数
次に記述されているのはhash関数とnoise関数です。
これらに関しては前回のコードリーディングの記事で似た部分について言及しているのでそちらを見てもらうといいでしょう。
ざっくりとだけ説明しておくと、hash関数は引数が同じなら同じ値を返す関数です。
ここで使いたいものは「疑似乱数」でしょう。そして疑似乱数はhash関数同様、引数と種が同じなら同じ値を返す関数です。
つまりは「疑似乱数」を得ている、と見ていいでしょう。
FBM
そして冒頭での最後の関数はfbm関数です。
これは「Fractal Brownian motion」の略で、非整数ブラウン運動と訳されます。
これについては以前記事に書いたのでそちらを参照ください。
要は、雲のような波のうねり表現を加えてくれるもの、ですね。
距離関数の亜種
さて、次に見るのはscene関数です。
これは距離関数の亜種として利用されています。
scene関数は以下のように定義されています。
float scene(in vec3 pos)
{
return 0.1 - length(pos) * 0.05 + fbm(pos * 0.3);
}
ちょっと見慣れない形ですね。
ただ、ここで行っている処理をざっくりいうと、通常の球体の距離関数fbm関数でのノイズを混ぜたもの、という感じです。
ただし密度を計算している
少し注意してもらいたいのは、距離関数は本来、「とある点から該当オブジェクトまでの距離」を返す関数であるということです。
そして関数をよく見てみると、主な距離関数部分を「減算」する形になっていることに気づきます。
return 0.1 - length(pos);
さて、普通の球体の距離関数は以下です。
return length(pos) - 1.0;
計算が逆転していることが分かりますね。
そして、離れた位置からの計算をした場合(つまり上記関数で言えば0.1よりも離れた場所の場合)、計算結果はマイナスとなってしまいます。
これは、この関数が通常の距離関数ではく「密度」を返しているからです。
つまり、レイが球体の中に入った(0.1以下になった)ら、その値はプラスに転じます。
そしてレイが進むに連れてその値が変化し、仮に中心に向かっていくレイの場合はその値はマーチを繰り返すたびに大きくなり、さらに中心を抜けるとまた徐々に小さくなっていきます。
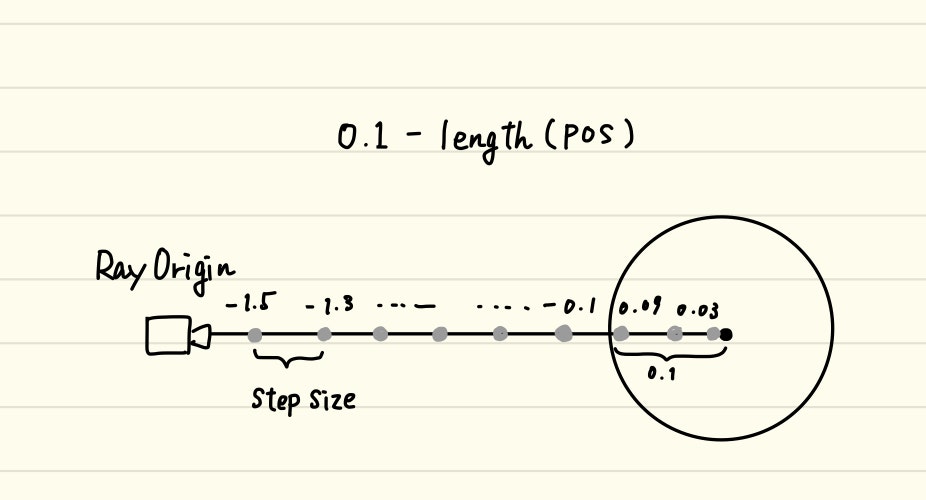
図にすると以下のような感じですね。
step size分ループするたびに進み、近づいていくにつれて関数が返す値は徐々に0に近づき、オブジェクトの中に入ったらプラスに転じる様子を示しています。
レイは「一定距離ずつ」進む
さて、もうひとつ注意点があります。
それは、通常のレイマーチングでは「一番近いオブジェクト」への距離分、レイが移動していきます。
しかし今回のレイマーチングではそうではなく、あらかじめ規定した距離(=一定距離)ずつ進んでいくことになります。
これは、不透明オブジェクトを描き出すのが目的ではなく、あくまで半透明である「雲」をレンダリングするため、一定の距離ごとにサンプリング点を取り、その位置からライト方向への密度をサンプリングしそれを累積することで雲の絵を描き出す、という手法のためです。
そのため、オブジェクトごとの最短距離、という判定ではなく一定距離ずつレイを進める必要がある、というわけなんですね。
main関数
さてではいよいよ、main関数の中身を見ていきましょう。
といっても、冒頭は通常のレイマーチと同様に、テクセルの位置を元にカメラ姿勢を適用してレイの方向を決める処理になります。
このあたりは以前書いたレイマーチング入門などにも書いているので詳細はそちらをご覧ください。
今回は雲のレンダリング処理部分に焦点を当てて書いていきたいと思います。
// For raymarching const values.
const int sampleCount = 64;
const int sampleLightCount = 6;
const float eps = 0.01;
// Raymarching step settings.
float zMax = 40.0;
float zstep = zMax / float(sampleCount);
float zMaxl = 20.0;
float zstepl = zMaxl / float(sampleLightCount);
// レイの視点(Ray Origin)を簡易アクセスするために`p`を定義
vec3 p = ro;
// Transmittance
float T = 1.0;
// 実質的には透明度
float absorption = 100.0;
// ライト方向
vec3 sun_direction = normalize(vec3(1.0, 0.0, 0.0));
// 計算結果用
vec4 color = vec4(0.0);
まず最初は変数のセットアップです。
サンプル回数を定義
sampleCountはレイマーチング自体のサンプルする点の数、sampleLightCountは、左記のサンプル点からライトへ向かうベクトル中のサンプルの数となっています。
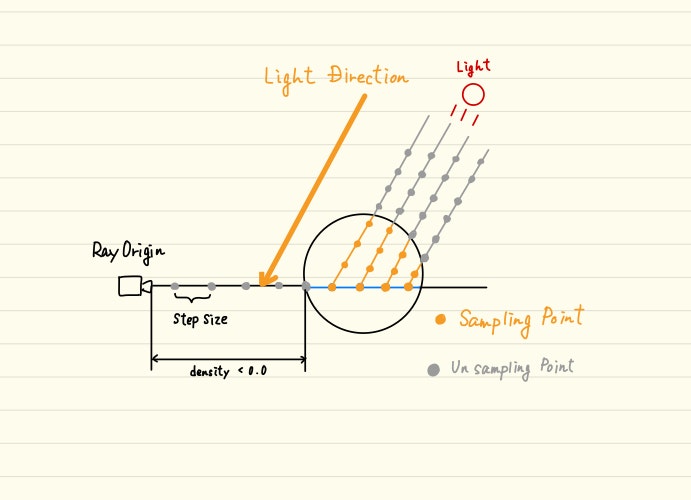
ちなみにこのサンプル点のイメージは以下になります。
まず、レイが前述の通り一定距離(step size)ずつ進んでいきます。
そしてレイがオブジェクト内に入っていたら、ライト方向に対してもサンプリングを行います。
ちなみにこれは最大、N * Mという計算量になり、とても高価な処理になります。
(N回のサンプル点に対して、ベクトル方向にもM回サンプルするため、最大でN * M回のサンプルが必要となります)
今回の例では64回のレイマーチングによるサンプルと、ライト方向への6回のサンプルを実行しているため、最大で384回のサンプリングが発生する計算になります。
距離関数が単純であればそこまで高負荷はなりませんが、複雑になればなるほどその影響が大きくなっていきます。
サンプル距離を計算
サンプル回数と最大サンプリング距離が決まれば自ずと一回のマーチで進むレイの距離が計算できます。
それを行っているのが以下の計算部分です。
// Raymarching step settings.
float zMax = 40.0;
float zstep = zMax / float(sampleCount);
float zMaxl = 20.0;
float zstepl = zMaxl / float(sampleLightCount);
上が通常のレイマーチング、下がライトへ向かうサンプルの距離です。
単純に、定めた距離をサンプル回数で割っているだけですね。
透過率・吸収率
さて、最後は以下の変数です。
(まだ説明していない変数もありますが、名称から分かる or コメントで説明できる範囲のものはコメントにしてあるのでそちらを見てください)
// Transmittance
float T = 1.0;
// Substantially transparency parameter.
float absorption = 100.0;
ここでTはTransmittance、つまり「透過率」ですね。透過率を計算結果に掛けることで徐々に不透明な感じを出していくための変数となります。
次のabsorptionは、英単語だけで言えば吸収という意味なので、光が吸収されたことを計算するために用いられるものだと思います。
つまり「どれだけ光を吸収するか」の値ですね。
計算部分を見てみると以下のようになっています。
T *= 1.0 - (tmp * absorption);
となっており、「密度 * absorption」を「1.0」から減算したものを透過率Tに掛けています。
吸収率absorptionの値が大きければ大きいほど光が吸収されるため、レイマーチング的には早々にリターンすることになります。
なので値が大きいほど雲は「透明に近く」なります。
実質的には「透明度(Transparency)」ということになりますね。
レイマーチング
さて、ではいよいよレイマーチング部分を見ていきましょう。
通常のレイマーチングと同様、指定した回数for文によってループさせます。
冒頭では距離関数を利用して「密度」を求めます。
float density = scene(p);
そしてそれがプラスに転じたらサンプリング開始です。
if (density > 0.0) { ... }
距離関数の亜種のところでも書きましたが、この関数は「密度」を返します。
つまり「雲の中」にレイがある場合は密度がある状態、「雲の外」にレイがある場合は密度がマイナスとすることで、うまく「雲の中」でだけサンプリングできるようにしている、というわけなんですね。
なので、プラスに転じた段階でサンプリングを開始しているわけです。
ちなみに、密度がマイナスの間は一定の距離ずつレイを進めていきます。
p += dir * zstep;
dirがレイの方向、zstepが事前に計算した1stepで進む距離です。
それを加算していくことでレイを進めています。
透過率計算
float tmp = density / float(sampleCount);
T *= 1.0 - (tmp * absorption);
透過率Tは、各サンプル単位に正規化(sampleCountで除算)した値を使って計算します。
また上で書いたように、absorptionを利用してどれくらい透過していくかも計算します。
そして透過率がしきい値(今回の例では0.01)を下回った場合はレイマーチングを終了します。
// Return if transmittance under 0.01.
// Because the ray is almost absorbed.
if (T <= 0.01)
{
break;
}
色の計算
実は密度だけの計算でいいならこれで計算は終わりです。
なので、#defineを使ってライトの有無を切り替えられるようにしてあります。
試しにUSE_LIGHTを1にしてみると色が加算され、より雲っぽくなります。
まずは光の計算部分をいったんスキップして、色を計算する部分を見てみましょう。
float opaity = 50.0;
float k = opaity * tmp * T;
vec4 cloudColor = vec4(1.0);
vec4 col1 = cloudColor * k;
// ... 中略 ...
color += col1;
cloudColorが雲自体の色です。上の例では「白(1.0, 1.0, 1.0)」ですね。
そして係数の計算は(実質的な)密度tmpに、透過率Tを掛け、さらにそれを50.0倍して、それを色に乗算することで求めています。
この50.0は実質的に不透明度(opaity)ということになりますね。
なのでこの値を小さくすると雲の色が薄くなります。
ここまでで、冒頭の雲の絵が描かれることになります。
光の計算を加える
さて、では光を加える計算を見てみましょう。以下の部分ですね。
// Light scattering
// Transmittance for Light
float Tl = 1.0;
// Start light scattering with raymarching.
// Raymarching position for the light.
vec3 lp = p;
// Iteration of sampling light.
for (int j = 0; j < sampleLightCount; j++)
{
float densityLight = scene(lp);
// If densityLight is over 0.0, the ray is stil in the cloud.
if (densityLight > 0.0)
{
float tmpl = densityLight / float(sampleCount);
Tl *= 1.0 - (tmpl * absorption);
}
if (Tl <= 0.01)
{
break;
}
// Step to next position.
lp += sun_direction * zstepl;
}
冒頭の変数たちはライト計算に使う透過率とサンプリングに使うレイの開始位置です。
(レイマーチング本体の位置を上書かないようコピーしています)
そして通常のレイマーチと同様に、光方向に向かってサンプリングを行っていきます。
レイマーチの計算はほぼ、本体のレイマーチングと同様ですね。方向がライト方向になっているのが異なるくらいでしょう。
そして本体と同様、透過率がしきい値以下になったらループを抜けています。
光の色を加算する
最後に、上記までで計算したTlを利用して光の色を加算します。
float opacityl = 30.0;
float kl = opacityl * tmp * T * Tl;
vec4 lightColor = vec4(1.0, 0.7, 0.9, 1.0);
vec4 col2 = lightColor * kl;
計算式自体は密度の計算で利用したものとほぼ同じですね。
違いは、係数の計算にTも利用して、T * Tlとなっている点くらいです。
色の計算
以上でコード全容を見てきました。
最後の色の計算部分について考えてみます。
計算式は、言葉で表すと
「不透明度 * 密度 * 透過率 * 色」
という形になっています。
透過率自体は以下の式になっていました。
float tmp = density / float(sampleCount);
T *= 1.0 - (tmp * absorption);
1.0から密度に吸収率を掛けたものを引いたものを累積(*=)したものですね。
おそらく、0.0〜1.0の間であることを期待している式だと思います。
(実際、試しにclamp(tmp * absorption, 0.0, 1.0)を追加してみましたが結果は変わりませんでした)
つまり、透過率は一方的に減っていく(少数値のみが掛けられる)ことになります。
そしてその累積した透過率がしきい値(0.01)を下回ったら、光がそれ以上進まないことを意味するのでループを終了しているわけですね。
まとめ
以上で雲のレイマーチングによるレンダリング方法を見てきました。
重要な点としては、
- 一定距離ずつレイを進める
- オブジェクト内にレイが入ったら、距離関数を元に密度を求める
- オブジェクト内点からライト方向にもサンプリングを行う
というあたりでしょうか。
今回は距離関数を利用して「密度」を計算していましたが、Volume Textureを使ったり、あるいは別の関数を使うなどして形状を他の方法で求めるようにすれば、色々な形の雲(や霧状のオブジェクト)なんかを描くのに使えそうですね。
また、各点におけるサンプリングの手法などは色々なことにも流用できそうなので使いみちがありそうです。
ただ、決して軽い処理ではないので、多様は禁物です。