はじめに
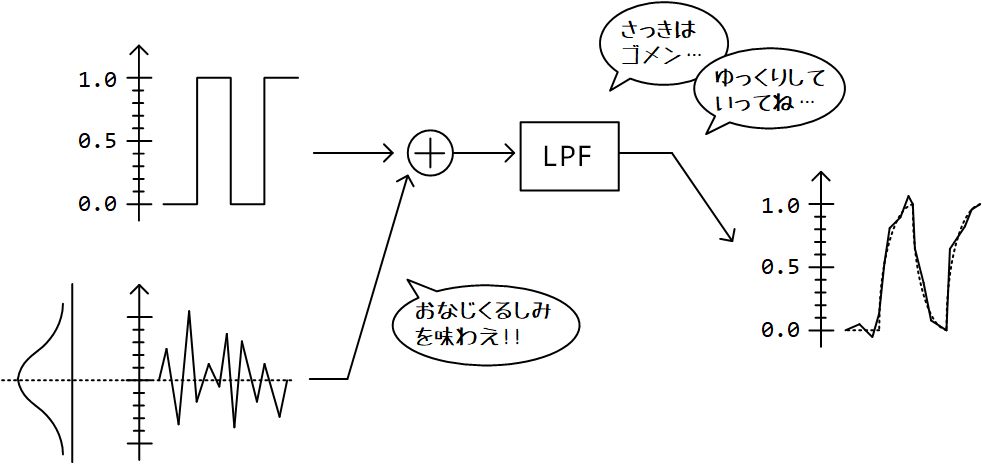
Verilogのシミュレータで表示されるデジタル信号って、きれいな形してますよね。現実世界では、シリコンもPCB上も職場も家も、ノイズばかりなのに。アナログ回路におぜん立てされた環境で、ぬくぬくとしているデジタル信号にも、私たちと同じ苦しみを味わってもらいましょう。
ノイズを入れつつ、波形もなまらせる
先ほどは、ついかっとなって、デジタル信号にノイズを食らわせてやるなんて、ひどいことを言ってしまいました。しかし、私は知っています、憎しみは何も生みません。悲しみの連鎖はここで終わらせるべきなのです。
……ということで、ノイズをぶち込んで気持ちがスッキリしたら、自分がやったことを反省し、デジタル信号にのせてしまったノイズを1次LPFでやさしく取り除いてあげましょう。「ごめん、あの時はどうかしていた」「もう絶対しないから許してほしい」と、相手に気持ちを伝えながら、ね1。
差分方程式を立てる
正規分布 $N(0, \sigma^2)$ に従うホワイトノイズ $\xi(t)$ を加えた場合、微分方程式は次のように書けます。
\begin{align}
&V_\mathrm{out}(t) + RC\frac{dV_\mathrm{out}(t)}{dt}
= V_\mathrm{in}(t) + \xi(t)\\
\therefore&
dV_\mathrm{out}
= \left(-\frac{1}{RC}V_\mathrm{out} + \frac{1}{RC}V_\mathrm{in}\right)dt
+ \frac{1}{RC} dW
\end{align}
つづいて、微小時間 $dt$ を有限の短さの時間ステップ $Δt$ で近似します。すると、次のような、時間ステップごとの出力電圧 $V_\mathrm{out}$ の差分を表す式が得られます。
\begin{align}
\Delta V_\mathrm{out}
&= \left(-\frac{1}{RC}V_\mathrm{out} + \frac{1}{RC}V_\mathrm{in}\right) \Delta t
+ \frac{1}{RC} \Delta W
\end{align}
上の式を使うと、出力電圧は最終的に次の差分方程式で表せます。
\begin{align}
V_\mathrm{out}[k+1]
&= V_\mathrm{out}[k]
+ \left(-\frac{1}{RC}V_\mathrm{out}[k]
+ \frac{1}{RC}V_\mathrm{in}[k]\right) \Delta t
+ \frac{1}{RC} \Delta W[k]\\
+ &= V_\mathrm{out}[k]
+ \left(-\frac{1}{RC}V_\mathrm{out}[k]
+ \frac{1}{RC}V_\mathrm{in}[k]\right) \Delta t
+ q[k]
\end{align}
ここで、$q[k]$ は正規分布 $N \left(0, \sigma^2\frac{\Delta t}{RC}\right)$ に従う乱数です。これは確率微分方程式2の数値解法の中でも最も素朴な方法であり、オイラー丸山法3と呼ばれています。
mutsumunemitsu - 確率微分方程式を数値計算してみよう
Mustafa Bayram - Numerical methods for simulation of stochastic differential equations
Numerical SDE Simulation - Euler vs Milstein Methods
Civil Engineering - Random Vibration
ボックスミューラー法を使う
ホワイトノイズを模擬するために、正規分布に従う乱数が必要です。しかし、SystemVerilogには、正規分布に従う real 型の乱数を生成する関数が用意されていません4。
ここでは、次式で表されるボックスミューラー法を使って、正規分布に従う real 型の乱数を生成します。
\begin{align}
&Z_0 = \sqrt{-2 \ln U_1} \cos(2\pi U_2)\\
&Z_1 = \sqrt{-2 \ln U_1} \sin(2\pi U_2)
\end{align}
上式をSystemVerilogで実装すると、次のようになります5。
今回は、ボックスミューラー法をSystemVerilogで直接実装しましたが、C言語で書いてDPI-Cで呼び出すというやり方もあるようです。HDL Advent Calendar 2015で紹介されています（今から5年前！）
mizutomo - SystemVerilogって正規分布関数ないんだってよ
module test;
timeunit 1s;
timeprecision 1ps;
function real rdist_normal (
input real mu,
input real sigma
);
localparam real pi = 4*$atan(1);
localparam real uint_max = $itor(2)**32 - 1;
real u1, u2;
real z0;
u1 = $urandom()/uint_max;
u2 = $urandom()/uint_max;
z0 = mu + sigma * $sqrt(-2*$ln(u1)) * $cos(2*pi*u2);
return z0;
endfunction
parameter int N = 200000;
int fd;
initial begin
fd = $fopen("rdist_normal.csv", "w");
for (int i=0; i<N; i++) begin
$fdisplay(fd, rdist_normal(0, 1));
end
$fclose(fd);
$finish();
end
endmodule
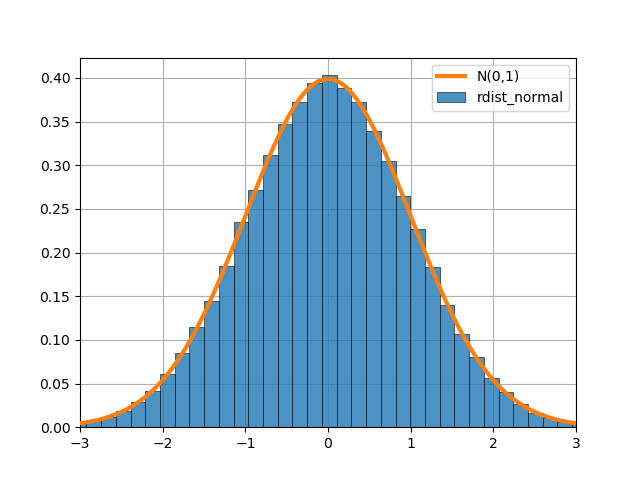
上のテストベンチで得られた乱数の確率分布を、正規分布と比較します。
import os
import pathlib
import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt
os.chdir(pathlib.Path("__file__").parent)
z = np.loadtxt("rdist_normal.csv")
plt.hist(
z,
bins=50,
density=True,
ec='black',
lw=0.5,
alpha=0.8,
zorder=2,
label="rdist_normal",
)
x = np.linspace(-3, 3, 301)
y = norm.pdf(x, 0, 1)
plt.plot(
x, y,
lw=3,
zorder=3,
label="N(0,1)",
)
plt.grid()
plt.legend()
plt.xlim([-3, 3])
plt.savefig("rdist_normal.png")
最終的に下図のような結果が得られます。
SystemVerilogで記述する
先ほど得られた差分方程式と乱数を使い、SystemVerilogで動作モデルを記述します。
module LPF1N #(
parameter realtime timestep = 100ps,
parameter real initial_vc = 0,
parameter real R = 1e3,
parameter real C = 500e-15,
parameter real sigma = 0.1
)(
input real VIN,
input real VSS,
output real VOUT
);
timeunit 1s;
timeprecision 1ps;
real _vin;
assign _vin = VIN - VSS;
event initial_step;
initial begin
#0;
-> initial_step;
end
event start_timer;
event stop_timer;
event next_step;
always @(start_timer, stop_timer) begin
if (start_timer.triggered()) begin
fork begin
#(timestep);
-> next_step;
end join_none
end else begin // stop_timer
disable fork;
end
end
function real rdist_normal (
input real mu,
input real sigma
);
localparam real pi = 4*$atan(1);
localparam real uint_max = $itor(2)**32 - 1;
real u1, u2;
real z0;
u1 = $urandom()/uint_max;
u2 = $urandom()/uint_max;
z0 = mu + sigma * $sqrt(-2*$ln(u1)) * $cos(2*pi*u2);
return z0;
endfunction
localparam realtime tau = R*C;
realtime t;
realtime last_t;
realtime delta_t;
real last_vin;
real vc;
real vn;
real delta_vc;
always @(initial_step, next_step) begin
if (initial_step.triggered()) begin
vc = initial_vc;
last_vin = _vin;
last_t = $realtime();
-> start_timer;
end else begin
-> stop_timer;
t = $realtime();
delta_t = t - last_t;
delta_vc = (-vc + last_vin)*delta_t/tau;
vc += delta_vc;
vn = rdist_normal(0, sigma*$sqrt(delta_t/tau));
last_vin = _vin;
last_t = t;
-> start_timer;
end
end
assign VOUT = vc + vn + VSS;
endmodule
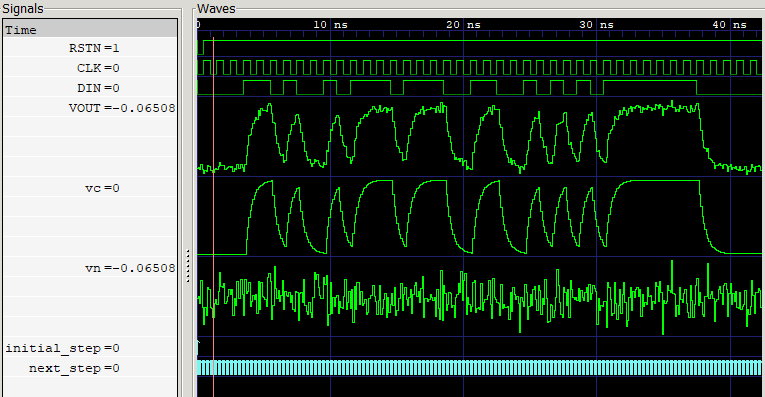
シミュレーション結果
- Simulator: ModelSim ALTERA STARTER EDITION vsim 10.5b Simulator 2016.10 Oct 5 2016
- Viewer: GTKWave Analyzer v3.3.71
おわりに
今日もおつかれさまなのじゃ
くたくたいふくに、やつれたおかお
よしよし、わらわにおまかせじゃ、そうじにせんたく、あったかごはん
-
「確率微分方程式」という単語に聞き覚えがない場合は、AIcia Solid Project - 確率微分方程式 がおすすめ。厳密な話をおいといて、ノリと感覚で説明してくれるので、何となく分かった気になれます。たぶん。 ↩
- ↩
-
SystemVerilogには、正規分布に従う乱数を生成する関数
$dist_normal()があります……が、実数ではなく整数を返すので、今回の用途には使えませんでした。 ↩ - ↩