More than 3 years have passed since last update.

デジタル信号をもっともっとなまらせよう

Last updated at 2020-12-03Posted at 2020-12-03

はじめに

もっともっと波形をなまらせたい

人間の欲望はとどまるところを知りません。
1次ができれば2次、2次ができれば3次……そうです、今さらもう後戻りはできません。
私たちには、もう、3次LPFを使うという選択肢以外、残されていないのです¹。

微分方程式を立てない

ここでは、波形をなまらせるために、下図のような3次LPFを使います。

上図から、3次LPFの出力電圧が満たすべき式として、次の3階の微分方程式が……方程式が……が……あーあー。

我々人類は怠惰な生き物です。キルヒホッフの法則から方程式を立てるなんていう、単調で面倒な作業は、何度もやりたくありません。鉛筆を片手に回路図や数式と向き合うよりも、ベッドに寝っ転がって、スマホを片手にホロライブや比良坂芽衣の配信を見ていたい。そう考えるのが自然でしょう。

記号回路解析を使わない

現在、私たちが直面している問題は、次の通りです。

3次LPFの出力電圧の計算をおこないたい。
でも、方程式を立てるという退屈な作業は回避したい。

実は、2番目の問題は、回路を数式のまま扱うことのできるシミュレータを使えば解決する可能性がある²……のですが、それだと前の記事と同じモデルを書いて終わり、となってしまいます。つまり私が何を言いたいかというと、「デジタル信号をなまらせる方法を色々紹介したい」というおのれの欲望を満たせないのは困る。この記事では無理にでも違う手法を紹介したい。そういうわけです³。

畳み込みを使う

任意の入力信号 $x(t)$ を与えたときの出力信号 $y(t)$ は、インパルス応答 $h(t)$ を使って次のように表せます⁴。前者は連続時間の場合、後者は離散時間の場合の式です。

\begin{align}
&y(t) = h(t)*x(t) = \int_{-\infty}^{\infty} h(\tau)\,x(t-\tau)\,d\tau\\
&y[n] = h[n]*x[n] = \sum_{m=-\infty}^{\infty} h[m]\,x[n-m]
\end{align}

現実世界では入力信号よりも先に出力信号が現れることはないため、入力信号が与えられた時刻を $t=0$ とすると、$t<0$ の積分を省略できます。また、損失のあるシステムのインパルス応答は時間とともに減衰するため、律儀に $t\rightarrow\infty$ まで積分せずに、適当な時刻で打ち切っても、大きな問題は起きないはずです。そこで、畳み込みを次式で近似します。

\begin{align}
&y(t) \approx \int_{0}^{t_\mathrm{stop}} h(\tau)\,x(t-\tau)\,d\tau\\
&y[n] \approx \sum_{m=0}^{N} h[m]\,x[n-m]
\end{align}

つまり、何らかの方法で、3次LPFのインパルス応答 $h[n]$ が得られれば、下図のような畳み込みによって出力電圧が計算できます。これは、いわゆるFIRフィルタです。

インパルス応答を求める

現実世界の伝送路のインパルス応答を取得しようとすると大変ですが⁵、幸いなことに、私たちがこの記事で扱っている3次LPFは、理想的な抵抗器とコンデンサで構成されています。そのため、回路シミュレータ上で、入力信号に対する応答を簡単に取得することができます⁶。

まず、下図のようなテストベンチを組み、3次LPFのステップ応答 $u[n]$ を求めます⁷。

つづいて、次のようにステップ応答 $u[n]$ からインパルス応答 $h[n]$ を求めます。

\begin{align}
&h[0] = 0\\
&h[n+1] = u[n+1] - u[n]
\end{align}

step_to_impulse.py

import os
import pathlib
import numpy as np

os.chdir(pathlib.Path(__file__).parent)
step_response = np.loadtxt("step_response_10ps.csv")
impulse_response = np.insert(np.diff(step_response[::10]), 0, 0)
np.savetxt("impulse_response_100ps.csv", impulse_response, fmt="%.8e")

最終的に、下図のようなインパルス応答 $h[n]$ が得られます。

SystemVerilogで記述する

先ほど得られたインパルス応答をもとに、SystemVerilogで3次LPFの動作モデルを記述します。

LPF3.sv

module LPF3 #(
  parameter string fname = "impulse_response_100ps.csv"
)(
  input real VIN,
  input real VSS,
  output real VOUT
);
  timeunit 1s;
  timeprecision 1ps;

  real _vin;
  assign _vin = VIN - VSS;

  real h [];
  real d [];
  int fd;
  string line;
  realtime timestep;
  event initial_step;

  initial begin
    // Get FIR coefficients.
    h = new [0];
    fd = $fopen(fname, "r");
    while (!$feof(fd)) begin
      $fgets(line, fd);
      if (line) begin
        h = new [h.size()+1](h);
        $sscanf(line, "%g", h[h.size()-1]);
      end
    end
    $fclose(fd);
    // Get time step.
    $sscanf(fname, "impulse_response_%dps", timestep);
    timestep = timestep*1ps;
    // Create delay elements.
    d = new [h.size()-1];
    // Start FIR filter.
    #0;
    -> initial_step;
  end

  event start_timer;
  event stop_timer;
  event next_step;

  always @(start_timer, stop_timer) begin
    if (start_timer.triggered()) begin
      fork begin
        #(timestep);
        -> next_step;
      end join_none
    end else begin // stop_timer
      disable fork;
    end
  end

  real _vout;

  always @(initial_step, next_step) begin
    if (initial_step.triggered()) begin
      _vout = h[0]*_vin;
      -> start_timer;
    end else begin
      -> stop_timer;
      // Shift
      for (int i=(d.size()-1); i>=0; i--) begin
        if (i < 1) begin
          d[i] = _vin;
        end else begin
          d[i] = d[i-1];
        end
      end
      // Convolution
      foreach (h[i]) begin
        if (i < 1) begin
          _vout = h[i]*_vin;
        end else begin
          _vout += h[i]*d[i-1];
        end
      end
      -> start_timer;
    end
  end

  assign VOUT = _vout + VSS;

endmodule

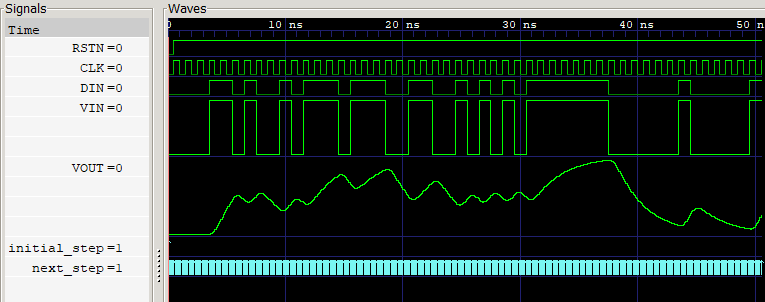
シミュレーション結果

Simulator: ModelSim ALTERA STARTER EDITION vsim 10.5b Simulator 2016.10 Oct 5 2016
Viewer: GTKWave Analyzer v3.3.71

今度こそ本当に

この「新台入替」みたいな画像はパチンコフォントメーカーを使って作成されました。 ↩
具体的な数値を代入せず、回路を数式のまま扱うような解析手法は、記号回路解析(Symbolic circuit analysis)と呼ばれます。少し古いですが、QSapecNG というソフトが無料で簡単に使えます。 ↩
このように、本来の目的を見失い、手段自体を目的にしてしまうことを、一般に「手段の目的化」と呼びます。わぁ。 ↩
やる夫で学ぶディジタル信号処理: たたみこみと積 - 線形時不変システムの入出力関係 ↩
現実世界の伝送路のインパルス応答を得る最も手軽な方法は、VNAで測定したSパラメータを逆フーリエ変換することです。ただし、この方法には面倒な問題がつきまといます。例えば、New Interconnect Models Removes Simulation Uncertaintyや、Preparing S-Parameters for Simulationを読むと、周波数領域の測定データを時間領域に持ってくることの難しさが、何となく感じられると思います。 ↩
「回路シミュレータが使えるなら、わざわざSystemVerilogで3次LPFの動作モデルを書く必要はない」「その回路シミュレータ上で、デジタル信号を3次LPFに通して、波形をなまらせればいいじゃないか」……ええ、そうです、その通りです。でも、いいじゃないか、にんげんだもの。 ↩
今回はQucsを使ってステップ応答を計算しました。無料で使える回路シミュレータの中では珍しく、Touchstone形式のSパラメータの読み込みに対応しています。GUIがKeysightのADSに少し似ている……ような気がしなくもない。 ↩

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up