はじめに

Verilogのシミュレータで表示されるデジタル信号って、立上りエッジや立下りエッジがシュッとしてて、なんだか見ていてつらいですよね。肩肘張ってちょっと無理して働いているかんじ。たまにはアナログ信号みたいに、波形をゆっくり変化させてあげましょう。

波形をなまらせる手順

デジタル信号の立上りや立下りが緩やかになることを、しばしば、「波形がなまる」と表現します。波形をなまらせる最も簡単な方法は、低域通過フィルタ (LPF: Low-pass filter) を掛けることです。この記事では、下図のように、デジタル値をアナログ値に変換 (D2A = Digital to Analog) したあと、LPFを掛けるという手順で、デジタル信号をなまらせます。

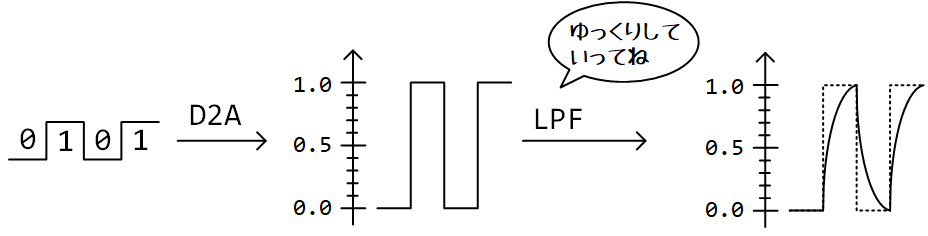
最初のD2Aは、2値型や4値型の0/1を、real型の実数値に変換する処理です。例えば、assign analog_value = digital_value ? 1.0 : 0.0;のように記述できます。この記事ではD2A後のLPF部分に焦点を当てたいので、D2Aの説明はこの1行で終わりです。

微分方程式を解く

ここでは、波形をなまらせるために、下図のような1次LPFを使います。

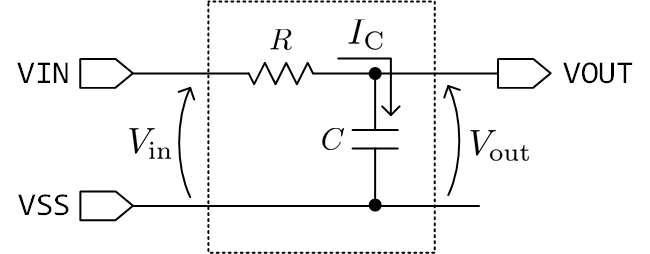
上図から、1次LPFの出力電圧が満たすべき式として、次の微分方程式が得られます。

\begin{align}
&V_\mathrm{out}
= V_\mathrm{in} - R \times I_\mathrm{C}
= V_\mathrm{in} - R \times C\frac{dV_\mathrm{out}}{dt}\\
&\therefore
V_\mathrm{out} + RC\frac{dV_\mathrm{out}}{dt}
= V_\mathrm{in}
\end{align}

この微分方程式を解いて、$V_\mathrm{out}(t)$ を求めます。過渡現象論や微分方程式の教科書を引っぱり出して、学生時代を思い出しながら手計算で解く……のは面倒なので、今回はWolframAlphaを使います。

>>> solve x + b*dx/dt = a for x, x(0)=c
x(t) = e^(-t/b) (a (e^(t/b) - 1) + c)

したがって、1次LPFの出力電圧を次式で表せます。

\begin{align}
&V_\mathrm{out}(t)
= V_\mathrm{in}(t)
- V_\mathrm{in}(t)\,e^{\displaystyle -\frac{1}{RC}t}
+ V_\mathrm{out}(0)\,e^{\displaystyle -\frac{1}{RC}t}
\end{align}

SystemVerilogで記述する

先ほど得られた出力電圧の式をもとに、SystemVerilogで1次LPFの動作モデル¹を記述します。

1次LPFの出力電圧は、時定数 $\tau = RC$ の5倍の時間で最終値の99%に到達します²。このことを考慮し、入力電圧が変化してから $5 \tau$ 経過した時点で、出力電圧に $t\rightarrow\infty$ の値を代入し、次に入力電圧が変化するまで、出力電圧の計算を行わないようにしています。

LPF1.sv

module LPF1 #(
  parameter realtime timestep = 100ps,
  parameter real initial_vc = 0,
  parameter real R = 1e3,
  parameter real C = 500e-15
)(
  input real VIN,
  input real VSS,
  output real VOUT
);
  timeunit 1s;
  timeprecision 1ps;

  real _vin;
  assign _vin = VIN - VSS;

  event vin_changed;
  always @(_vin) begin
    -> vin_changed;
  end

  event start_timer;
  event stop_timer;
  event next_step;

  always @(start_timer, stop_timer) begin
    if (start_timer.triggered()) begin
      fork begin
        #(timestep);
        -> next_step;
      end join_none
    end else begin // stop_timer
      disable fork;
    end
  end

  localparam realtime tau = R*C;
  realtime t0;
  realtime t;
  real vc0 = initial_vc;
  real vc = initial_vc;

  always @(vin_changed, next_step) begin
    -> stop_timer;
    if (vin_changed.triggered()) begin
      t0 = $realtime();
      vc0 = vc;
      -> start_timer;
    end else begin // next_step
      t = $realtime() - t0;
      if (t > 5*tau) begin
        vc = _vin;
      end else begin
        vc = _vin - (_vin - vc0)*$exp(-t/tau);
        -> start_timer;
      end
    end
  end

  assign VOUT = vc + VSS;

endmodule

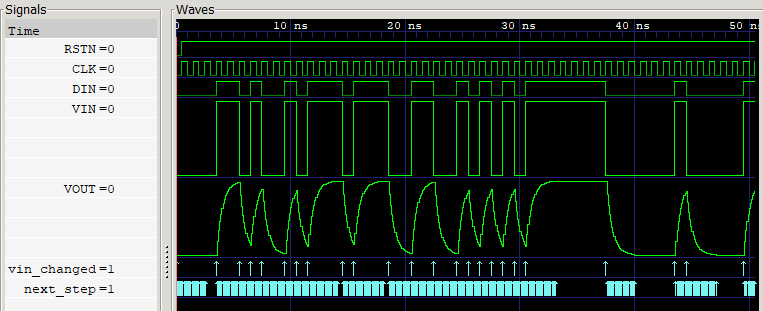
シミュレーション結果

Simulator: ModelSim ALTERA STARTER EDITION vsim 10.5b Simulator 2016.10 Oct 5 2016
Viewer: GTKWave Analyzer v3.3.71

おわりに

こんな記事を最後まで見てくれてありがとう³。

英語で言うところの Behavioral model、Functional model のこと。もしあなたがこの分野に興味があるなら、International Behavioral Modeling and Simulation Conference のアーカイブにある多くの資料を目の前にして、「ち…わきにく…おどるとはこのことだ」てきな気持ちの高ぶりを感じることでしょう。そして、トップページの「After several years of sagging attendance aggravated by the economic down turn, BMAS ceased operations after the 2010 workshop. (訳: BMASは数年に渡る景気悪化の影響で出席者数が減少した後、2010年のワークショップ終了後に運営を停止しました)」という一文に気づき、あ……(察し) ↩
Basic Electronics Tutorials and Revision - RC Charging Circuit ↩
この分野、日本語で書かれた情報が少ないので、ちょっとさみしい。そんななか、率先してネット上にこの分野の情報を流してくれている、下記のような神や仏のような人もいて、(恥ずかしいので絶対言いませんが) めっちゃリスペクトしてます。はやく続きがアップロードされないかな、投稿されないかな、って毎日ワクワクしながら、何度も同じページを開いたり閉じたりしています。つづきまだかな……まだかな…… ↩
- wyamamo74212 - Real Number Modeling (RNM) 超・初級編
- mizutomo - wrealを使ったアナログ風シミュレーション

デジタル信号をなまらせよう