記事の趣旨
ROC曲線について勉強している際に、真陽性率や特異度、検出力といった指標の関係性があやふやになってきたので、個人的な備忘として整理したいと思います。誤り等がありましたら、コメントいただけると嬉しいです。
指標の整理(1) 混同行列とその周辺
この章の執筆では以下を参考にさせていただきました。
混同行列
**混同行列(confusion matrix)**は実際の結果(正解ラベル)と予測した結果(予測ラベル)の関係についてまとめた以下のような表を指します。実際の結果と予測した結果の組み合わせから、個別のデータが下表の各要素のようにラベリングされることになります。
| 陽性と予測 | 陰性と予測 | |
|---|---|---|
| 実際に陽性 | 真陽性(TP; True Positive) | 偽陰性(FP; False Negative) |
| 実際に陰性 | 偽陽性(FP; False Positive) | 真陰性(TN; True Nagetive) |
この表を列方向(横方向)に見たときに、実際の結果(実際に陽性か実際に陰性か)に基づいて予測性能を測る指標が以下の4つです。
- 真陽性率(TPR; True Positive Rate):実際に陽性の人を正しく陽性と予測した割合
- 偽陽性率(FPR; False Positive Rate):実際には陰性の人を誤って陽性と予測した割合
- 偽陰性率(FNR; False Negative Rate):実際には陽性人を誤って陰性と予測した割合
- 真陰性率(TNR; True Negative Rate):実際には陰性の人を正しく陰性と予測した割合
感度と特異度
上の指標のいくつかには別名があり、真陽性率は感度(sensitivity)、真陰性率は**特異度(specificity)**とも呼ばれます。つまり、
- 真陽性率 = 感度(sensitivity)
- 偽陽性率 = 1 - 特異度
- 偽陰性率 = 1 - 感度
- 真陰性率 = 特異度(specificity)
となります。感度と特異度はそれぞれ医学系(疫学系)でよく用いられる用語らしいです。PCR検査を例にとると、感度は「ウイルス感染者の何%を陽性だと判断できるか」、特異度は「ウイルス非感染者の何%を陰性と判断できるか」を表しています。日本疫学会のQ&Aによると、コロナウィルスに対するPCR検査の感度は発症日(感染後5日目)で62%です。つまり感染者のうち62%が正しく陽性と判断され、残りの38%は陰性と判断されてしまうということになります。
適合率と再現率
混同行列に関連した評価指標として更に以下の4つがあります。
正解率(Accuracy):全ての予測のうち正しく予測できた割合
適合率(Prescison):陽性と予測したデータのうち実際に陽性の割合
再現率(Recall):陽性の人を正しく陽性と予測した割合
F1値(f1 score):適合率と再現率の調和平均
ここでの個人的な注目点は**「再現率=真陽性率=感度」**ということです。それぞれの概念を出会すたびに確認していたのでスッキリしました。ちなみにF1値が調和平均として定義されているのは、適合率と再現率が二律背反の関係にあることを踏まえ、これらをバランスよく評価する目的があるからです。
仮説検定との関係
続いて、第一種の過誤(type1 error)、第二種の過誤(type2 error)、**検出力(testing power)**との関係です。これらの用語は統計的仮説検定の文脈で使われる用語ですが、上記の指標と深い関連性があります。仮説検定の概要はwikiや統計学の教科書に譲りますが、第一種の過誤と第二種の過誤はそれぞれ
- 第一種の過誤:本来正しい帰無仮説を棄却してしまうこと
- 第二種の過誤:本来誤っている帰無仮説を棄却できないこと
を意味しています。**ここで「帰無仮説を棄却する=陽性」と考えると、第一種の過誤は偽陽性、第二種の過誤は偽陰性と言えることが分かります。**またここで、帰無仮説が正しいときに正しく棄却できる割合を検出力といいます。つまり、検出力は第二種の過誤を犯さない可能性のことをさすので、1-偽陰性率=1-(1-感度)=感度となります。つまり、検出力=感度=真陽性率です。
| 陽性と予測(帰無仮説を棄却) | 陰性と予測(帰無仮説を採択) | |
|---|---|---|
| 実際に陽性 | 真陽性 | 第二種の過誤(偽陰性) |
| 実際に陰性 | 第一種の過誤(偽陽性) | 真陰性 |
まとめ
見づらいですが、以上をまとめると下表のようになります。
| 陽性と予測 | 陰性と予測 | |
|---|---|---|
| 実際に陽性 | 真陽性率 = 感度 = 再現率 = 検出力 | 偽陰性 = 1-感度 = 第二種の過誤 |
| 実際に陰性 | 偽陽性率 = 1-特異度 = 第一種の過誤 | 真陰性率 = 特異度 |
指標の整理(2) ROC-AUCとPR-AUC
この章の執筆では以下を参考にさせていただきました。
- PR曲線とROC曲線を理解する(後編)
- ROC曲線とPR曲線の違いについての考察
- ROC曲線とPR曲線の違いについての考察 - 続き
- ROC曲線とPR曲線-分類性能の評価方法を理解する②
- 機械学習の評価指標 分類編:適合率や再現率、AUC(ROC曲線、PR曲線)を解説
- ROC曲線の書き方を整理する。
- インバランスデータにおけるPR曲線とROC曲線の振る舞いの違い
ROC曲線とAUC
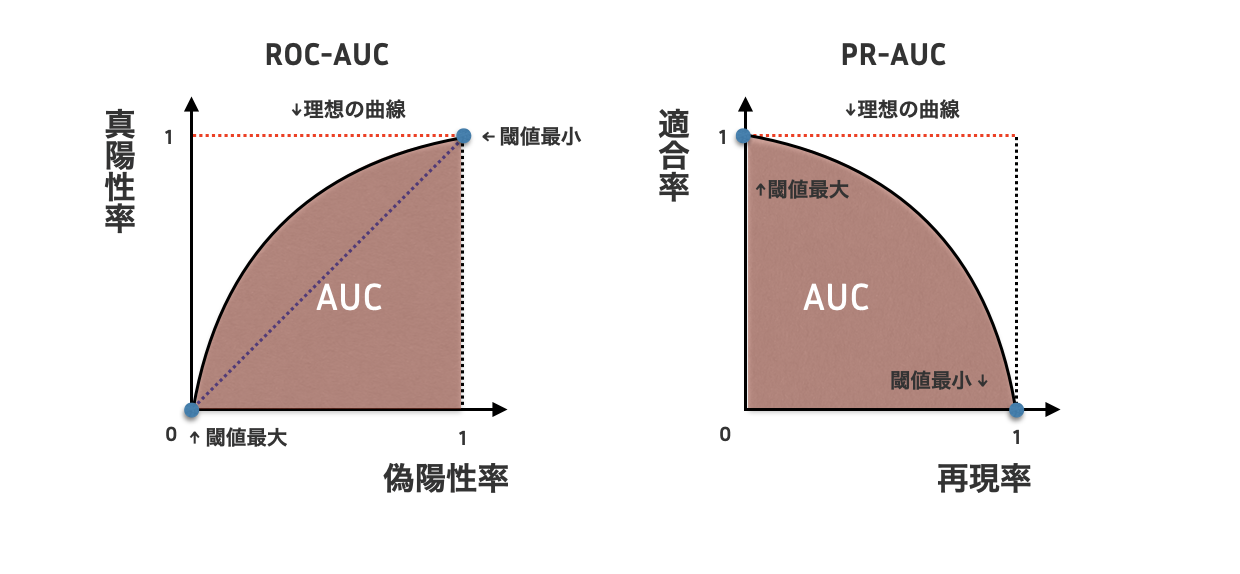
ROC曲線は縦軸に真陽性率(検出力)、横軸に偽陽性率(第一種の過誤)をとったものです。分類器(決定木やロジスティック回帰など)が判定に用いる閾値を変化させたときの、真陽性率と偽陽性率の関係性を示しています。つまり、各閾値の下での分類結果に基づいて真陽性率と偽陽性率を計算し、ひとつずつプロットしたものです。閾値を高くする(=陽性の判定基準を厳しくする)と陽性と判定されにくくなるので、真陽性率も偽陽性率も0に近づきます。一方で閾値を低くする(=陽性の判定基準を緩くする)と陽性と判定されやすくなるので、真陽性率も偽陽性率も1に近づきます。ここで問題なのは、閾値を低くしていった時の真陽性率の偽陽性率に対する増加具合です。これを見ることで、分類器同士の性能比較や、ある分類器で使用する閾値を設定するのに役立ちます。もし真陽性率と偽陽性率が同じ割合で増えるのであれば曲線は45度線に一致します。真陽性率の増加幅の方が大きい(実際に陽性の人を拾える場合の方が多いのであれば)、グラフは左上に膨らむことになります。ACU(Area Under the Curve)はROC曲線はの下側の面積のことであり、0から1までの値をとります。ROC曲線の曲がり具合を目で評価するのは難しいので、実際にはAUCの値を利用することが多いと思われます。
PR曲線とAUC
PR曲線は縦軸に適合率、横軸に再現率をとったものです。これもROC曲線と同様に考えることができ、ある各閾値の下での分類結果に対して適合率と再現率を計算し、一つずつプロットしたものです。閾値を高くする(=陽性の判定基準を厳しくする)と陽性と判定されづらくなるので、適合率は増加し、再現率は減少します。一方で閾値を低くする(=陽性の判定基準を緩くする)と陽性と判定されやすくなるので、適合率は減少し、再現率は増加します。適合率を減らさずに再現率を増やせるほど、つまり望ましい分類器ほどグラフは右上に膨らむことになります。AUCの定義は上のROC曲線の場合と同じで、値が大きいほど望ましいと言えます。
ROC曲線とPR曲線の比較
これらはどちらも分類器同士の性能比較や、ある分類器で使用する閾値を設定するのに役立つ指標です。実際には両方曲線を見ることが多いと思いますが、その違いとして、ROC曲線は分類器の大まかな性能を測るのに適しており、PR曲線は特に陰性のケースが多い場合(不均衡データの場合)の評価に適しているようです。この辺りは上にあげた記事のいくつかが詳しいです。
まとめ
2値分類の評価に使われる紛らわしい用語を簡単にまとめてみました。分かりづらい点や、説明の誤りなどありましたら、ご指摘いただけると幸いです。