はじめに
前回の記事 ではROC曲線とPR曲線の違いに着目して,実験的に性質の違いをあぶり出してみました.ただ原理的な納得度はまだイマイチですよね.
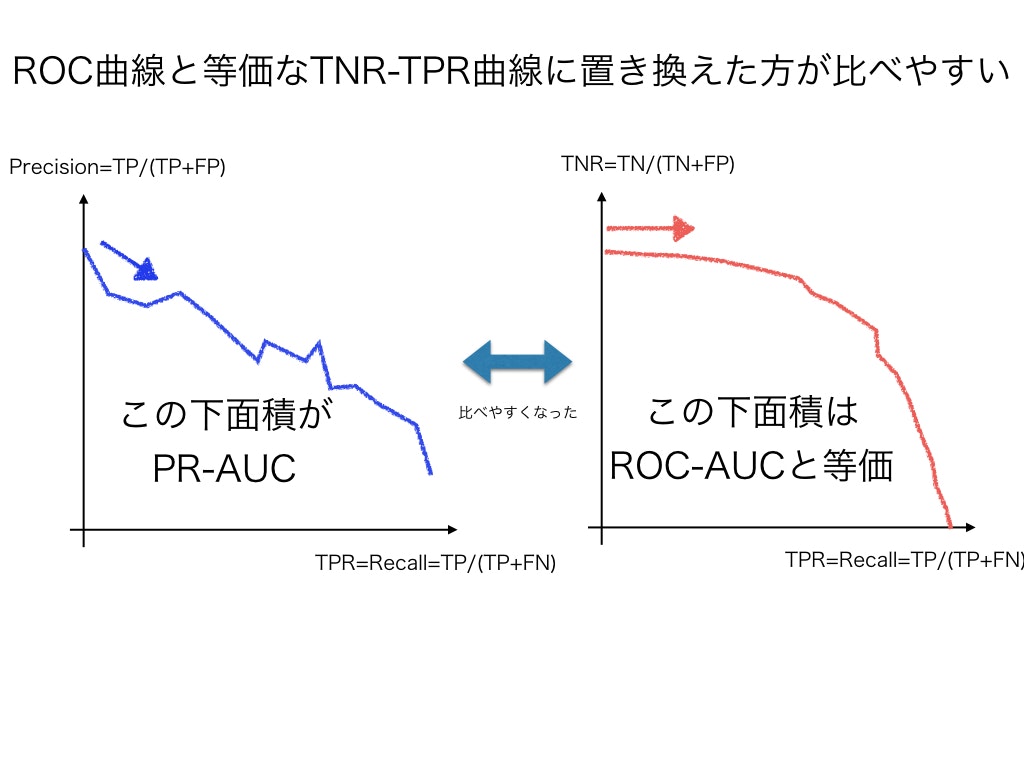
今度は, ROC曲線を等価な別の曲線と置き換えることで,よりPR曲線と比較しやすく してみたいと思います.
ROC曲線と等価な曲線
ROC曲線とPR曲線の比較しにくさは,
- ROC曲線は横軸が「小さいほうが嬉しい軸」,縦軸が「大きい方が嬉しい軸」
- PR曲線は縦軸も横軸も「大きい方が嬉しい軸」
となっていることに由来するのではと考えました.
PR曲線の縦軸Precisionと横軸Recallは,どちらも大きい方が嬉しいけど,互いにトレードオフになっていて両得は難しい,という極めて現実的に解釈しやすい軸担っていると思っています.そこで,ROC曲線の方も,縦軸と横軸が両方「大きい方が嬉しい軸」に変換してやれないでしょうか.
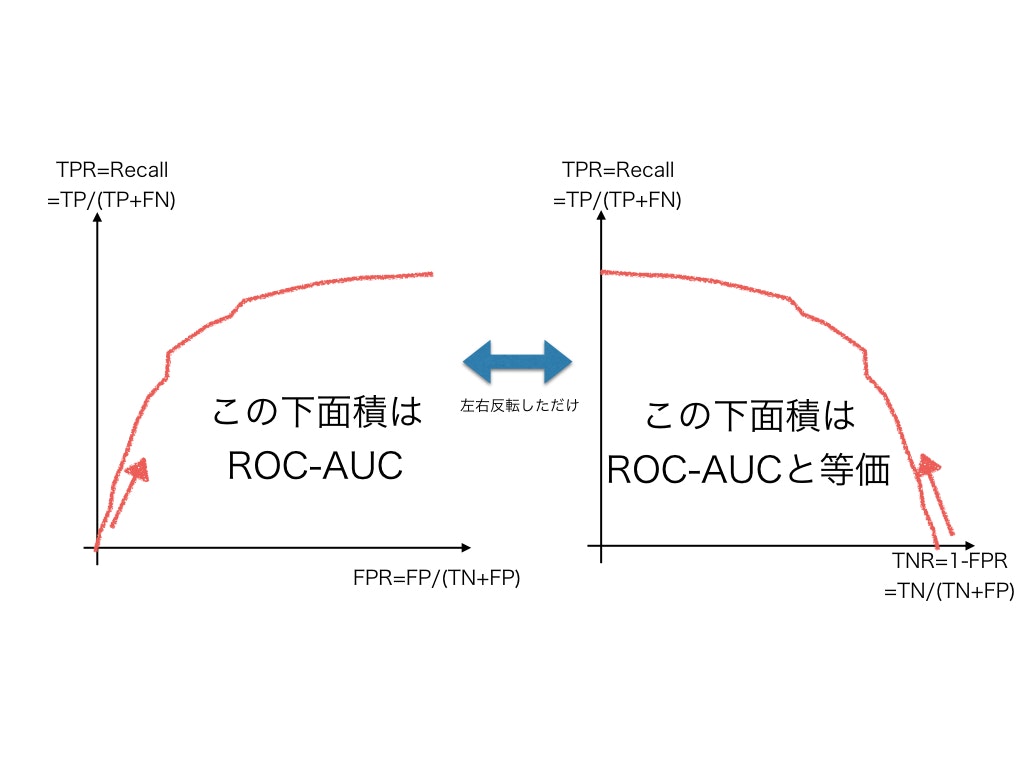
ROC曲線の横軸FPR=False Positive Rate は,TNRと FPR+TNR=1 の関係にあります.
ですので,ROC曲線の横軸をFPRから TNR=1-FPR に置き換えてやることでちょうどROC曲線とは左右を反転させたような曲線を得ることができます.
さらに縦軸と横軸を入れ替えてやると,ROC曲線と等価で,かつPrecision-Recall曲線と軸の意味合いがよく似たTNR-TPR曲線を得ることができます.これでROC曲線を直接考えるよりも比べやすくなったのではないでしょうか.
(ROC曲線と等価な)TNR-TPR曲線の形状と,負例の割合の関係
さて,各所でよく言及されているように
TNの値が大きくなりやすい場合にROC曲線よりPR曲線が一般的に適している
とは一体どういうことでしょうか.
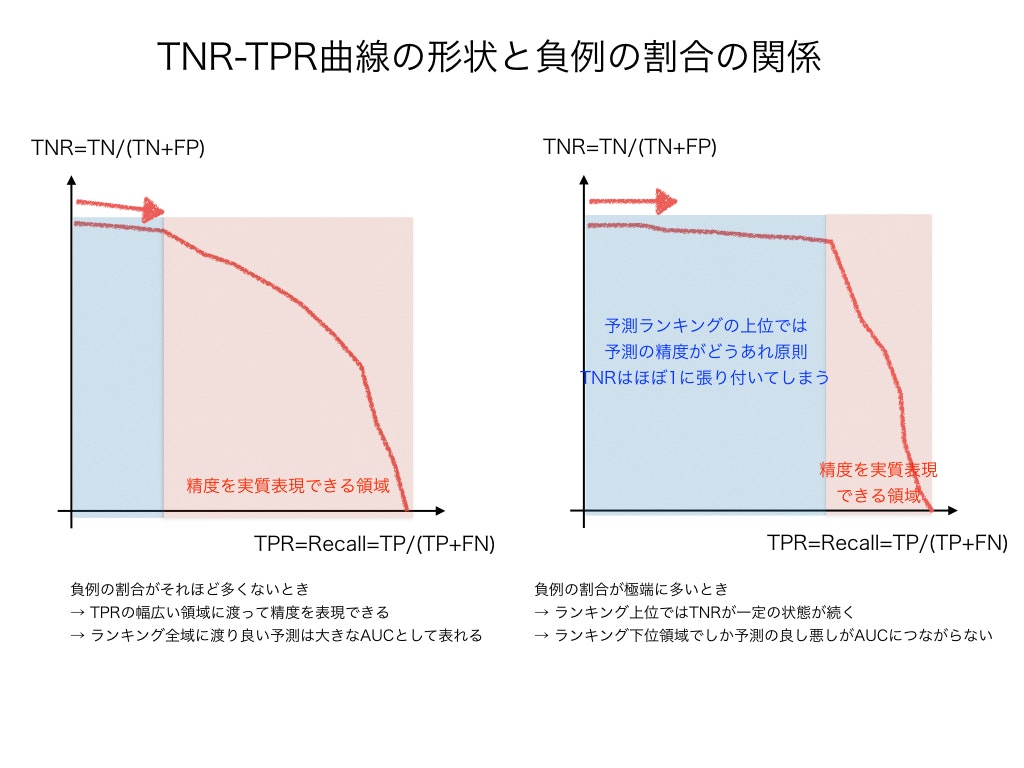
超定性的に言うと,(ROC曲線と等価な)TNR-TPR曲線は,正例に対して負例の割合が極端に大きくなるような予測問題に対しては,表現力がガクンと落ちてしまいます.
このイメージ図にあるように,正例と負例との割合があまり変わらなければば,TNR-TPR曲線は,横軸TPRの広い領域にわたって予測精度を表現できます.
一方で,正例に対して負例が極端に多いときは,予測ランキングの上位付近ではほぼほぼTN>>FPとなってしまい,TPRがそれなりに大きくなるまでは,TNRはほぼ1から張り付いて動きません.
したがってTPRがまだ小さいような予測ランキング上位付近でどれだけ良い精度が出せたところで,それはAUCの向上としては顕著には現れてこず,逆に予測ランキング下位付近で多少良い精度が出せれば,AUCは大きく動く,ということになります.
これは前回の記事の実験結果とも整合しています.
結論
以上が,「TNの値が大きくなりやすい場合にROC曲線が適していない」と言われる所以なのだと思います.まだまだ納得度は微妙ですが,ROC曲線はTNR-TPR曲線に置き換えることでPR曲線と比較しやすくできる,というのは嬉しい発見でした.
もしまだ考察を深めたい方がいらっしゃれば,ぜひこのTNR-TPR曲線を利用してみてください.