はじめに
機械学習の分類タスクにはその目的に応じて幾つかの性能評価指標があります。二項分類の主な性能評価指標であるROC曲線やPR曲線、そしてそのAUC(曲線の下側面積)についてまとめます。
参考
ROC曲線とPR曲線の理解にあたって下記を参考にさせていただきました。
分類タスク
文書分類タスクの具体例を交えて性能評価方法の説明を行います。その前段としてこの章では分類タスクの実施手法を簡単に記載しますが、分類タスク自体についての記事ではないためモデルの詳細な解説は省いています。
使用したライブラリ
- numpy 1.15.4
- lightgbm 2.3.1
- pandas 0.25.1
- scikit-learn 0.22.2
データセット
今回データセットは「livedoor ニュースコーパス」を使用しています。データセットの詳細やその形態素解析の方法は以前投稿した記事で投稿をご参照ください。
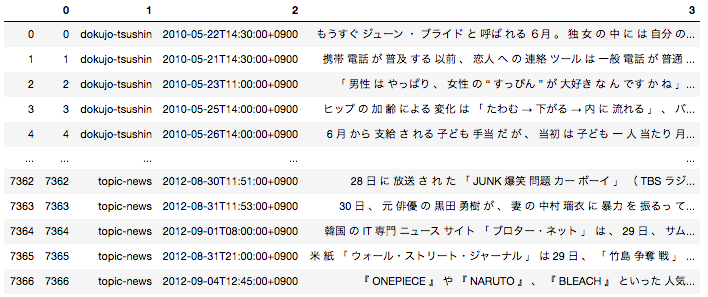
日本語の場合は事前に文章を形態素単位に分解する前処理が必要となるため、全ての文章を形態素に分解した後下記のようなデータフレームに落とし込んでいます。
一番右のカラムが文章を全て形態素解析して半角スペースごとに区切ったものになります。こちらを使用して分類タスクを実施します。
モデルの作成と分類の実施
今回は「Peachy」の記事と「独女通信」の記事(どちらも女性向けの記事)を分類します。今回は二項分類であるため、「独女通信」の記事か否かを判定する分類タスクと同義になっています。データセットを7:3に分割し、7を学習用、3を評価用にしています。
import pandas as pd
import numpy as np
import pickle
from sklearn.feature_extraction.text import TfidfVectorizer
# 形態素分解した後のデータフレームはすでにpickle化して持っている状態を想定
with open('df_wakati.pickle', 'rb') as f:
df = pickle.load(f)
# 今回に2つの種類の記事を分類できるかを検証
ddf = df[(df[1]=='peachy') | (df[1]=='dokujo-tsushin')].reset_index(drop = True)
vectorizer = TfidfVectorizer()
X = vectorizer.fit_transform(ddf[3])
def convert(x):
if x == 'peachy':
return 0
elif x == 'dokujo-tsushin':
return 1
target = ddf[1].apply(lambda x : convert(x))
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, target, train_size= 0.7, random_state = 0)
import lightgbm as lgb
from sklearn.metrics import classification_report
train_data = lgb.Dataset(X_train, label=y_train)
eval_data = lgb.Dataset(X_test, label=y_test)
params = {
'boosting_type': 'gbdt',
'objective': 'binary',
'random_state':0
}
gbm = lgb.train(
params,
train_data,
valid_sets=eval_data,
)
y_preds = gbm.predict(X_test)
こちらで予測が完了しました。y_predsにはその文書が「独女通信」である確率の値が入っています。
分類性能の評価方法
ROC曲線とPR曲線を見ていく前にその前段である混合行列について復習しておきます。
混合行列は二項分類タスクの出力結果をまとめたマトリクスで、下記のように表されます。
| Positiveと予測された | Negativeと予測された | |
|---|---|---|
| 実際にPositiveクラスに属する | TP(真陽性) | FN(偽陰性) |
| 実際にNegativeクラスに属する | FP:(偽陽性) | TN(真陰性) |
混合行列の中の各値を使用してROC曲線を描くことができます。
ROC曲線
ROC曲線の概要
\text{FPR} = \frac{FP}{TN + FP}
\text{TPR(recall)} = \frac{TP}{TP + FN}
ROC曲線とは$\text{FPR}$(偽陽性率)に対する$\text{TPR}$(真陽性率)をプロットしたものです。
このプロットが何を意味するのかという話ですが、まずは$\text{FPR}$と$\text{TPR(recall)}$の意味を具体例に当てはめて考えます。
{{\begin{eqnarray*}
\text{FPR} &=& \frac{分類モデルが「\text{Peachy}」の記事を誤って「独女通信」の記事であると予測した件数}{実際の「\text{Peachy}」の記事の全件数} \\
\end{eqnarray*}}}
{{\begin{eqnarray*}
\text{TPR(recall)} &=& \frac{分類モデルが「独女通信」の記事であると予測した結果が正解であった件数}{実際の「独女通信」の記事の全件数} \\
\end{eqnarray*}}}
この意味を整理すると下記のように言えます。
- $\text{FPR}$は誤って陽性(「独女通信」の記事)と分類された陰性(「Peachy」の記事)データの割合を表している→陰性データの判別の不正確さ表している(低いほど良い)
- $\text{TPR}$は正しく陽性(「独女通信」の記事)と分類された陽性(「独女通信」の記事)データの割合を表している→陽性判定の網羅性を表している(高いほど良い)
つまり、$\text{FPR}$が低い状態でありながら$\text{TPR}$が高いというのが理想的です。
様々な閾値における$\text{FPR}$と$\text{TPR}$をプロットすることでROC曲線を描くことができます。「$\text{FPR}$が低い状態でありながら$\text{TPR}$が高いというのが理想的である」ということを考えると、ROC曲線のカーブの形が直角に近いほどよい=AUC(ROC曲線の下側面積)が大きいほどよい、という発想に繋がっていきます。
ROC曲線の描画
ROC曲線を実際に描画してみましょう。
from sklearn import metrics
import matplotlib.pyplot as plt
fpr, tpr, thresholds = metrics.roc_curve(y_test, y_preds)
auc = metrics.auc(fpr, tpr)
print(auc)
plt.plot(fpr, tpr, label='ROC curve (area = %.2f)'%auc)
plt.plot(np.linspace(1, 0, len(fpr)), np.linspace(1, 0, len(fpr)), label='Random ROC curve (area = %.2f)'%0.5, linestyle = '--', color = 'gray')
plt.legend()
plt.title('ROC curve')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.grid(True)
plt.show()
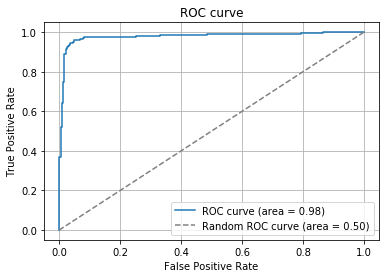
今回作成した分類器を用いてROC曲線を描画しました。ROC曲線の曲線が直角に近く、AUCが$0.98$(最大値が$1$)であることを考えると非常に精度が良いことがわかるかと思います。ランダムの分類器の場合AUCは$0.5$となることが決まっているため、ランダムとの比較の容易です。
PR曲線
PR曲線の概要
\text{precision} = \frac{TP}{TP + FP}
\text{recall(TPR)} = \frac{TP}{TP + FN}
PR曲線とは$\text{recall}$(再現率)に対する$\text{precition}$(適合率)をプロットしたものです。
このプロットが何を意味するのかという話ですが、まずは$\text{precition}$と$\text{recall}$の意味を具体例に当てはめて考えます。
{{\begin{eqnarray*}
\text{precision} &=& \frac{分類モデルが「独女通信」の記事であると予測した結果が正解であった件数}{分類モデルが「独女通信」の記事であると予測した全件数} \\
\end{eqnarray*}}}
{{\begin{eqnarray*}
\text{recall} &=& \frac{分類モデルが「独女通信」の記事であると予測した結果が正解であった件数}{実際の「独女通信」の記事の全件数} \\
\end{eqnarray*}}}
- $\text{precision}$は分類モデルが陽性と分類したデータ内、本当に陽性(「独女通信」の記事)であるデータの割合を表している→陽性判定の確からしさを表している(高いほど良い)
- $\text{recall}$は正しく陽性(「独女通信」の記事)と分類された陽性(「独女通信」の記事)データの割合を表している→陽性判定の網羅性を表している(高いほど良い)
つまり、$\text{precision}$が高い状態でありながら(確からしさを担保しながら)$\text{recall}$もできるだけ高い(網羅もできている)というのが理想的です。
様々な閾値における$\text{precision}$と$\text{recall}$をプロットすることでPR曲線を描くことができます。これもまたROC曲線と場合と同様にAUC(PR曲線の下側面積)が大きいほど精度が良いと言えます。
precision, recall, thresholds = metrics.precision_recall_curve(y_test, y_preds)
auc = metrics.auc(recall, precision)
print(auc)
plt.plot(recall, precision, label='PR curve (area = %.2f)'%auc)
plt.legend()
plt.title('PR curve')
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.grid(True)
plt.show()
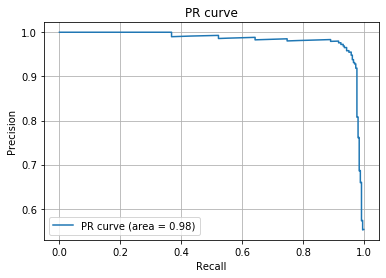
今回作成した分類器を用いてPR曲線を描画しました。AUCが$0.98$(最大値が$1$)であることを考えると、PR曲線の観点で見ても非常に精度が良いことがわかるかと思います。ただROC曲線の場合とは違ってランダムの分類器の場合でおAUCは$0.5$となるとは限りません。
ROC曲線とPR曲線
ROC曲線とPR曲線のどちらを使えばよいのか、という話ですが一般的には不均衡データの場合(negativeの数がpositiveの数よりも圧倒的に多い等)はPR曲線を使い、それ以外はROC曲線を使用するのがよいとされています。
解釈としては、ROC曲線においてはPositiveをPositiveであると判断できていること、NegativeをNegativeと判断できること両方を観点として持っていますが、PR曲線はPositiveをPositiveと判断できるていることのみに着目しています。なので、分類器の性能指標としては両方のバランスを見ているROC曲線を使用するのがよいのですが、Negativeの方が圧倒的に多い場合は大多数のNegativeをNegativeと判断することによって精度が良いと判断されてしまいます。(Positveの判断は適当であっても。)なので、少数のPositiveをちゃんと判断できているか見るためにPR曲線を使用する、というのが私の見解です。
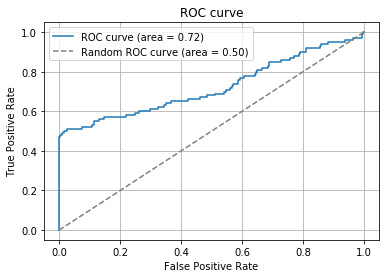
極端な例ですが、Positive100件のデータとNegative99900件のデータにおいて、Positiveは適当に予測し、NegativeはNegativeと確実に判断するモデルがあったとします。するとROC曲線とPR曲線は下記のようになります。
rand_predict = np.concatenate((np.random.rand(100) , 0.5*np.random.rand(99900)))
rand_test = np.concatenate((np.ones(100), np.zeros(99900)))
from sklearn import metrics
import matplotlib.pyplot as plt
fpr, tpr, thresholds = metrics.roc_curve(rand_test, rand_predict)
auc = metrics.auc(fpr, tpr)
print(auc)
# ROC曲線
plt.plot(fpr, tpr, label='ROC curve (area = %.2f)'%auc)
plt.plot(np.linspace(1, 0, len(fpr)), np.linspace(1, 0, len(fpr)), label='Random ROC curve (area = %.2f)'%0.5, linestyle = '--', color = 'gray')
plt.legend()
plt.title('ROC curve')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.grid(True)
plt.show()
## PR曲線
precision, recall, thresholds = metrics.precision_recall_curve(rand_test, rand_predict)
auc = metrics.auc(recall, precision)
print(auc)
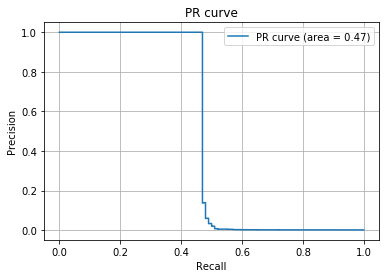
plt.plot(recall, precision, label='PR curve (area = %.2f)'%auc)
plt.legend()
plt.title('PR curve')
plt.xlabel('Recall')
plt.ylabel('Precision')
plt.grid(True)
plt.show()
AUCに大きな差があることがわかるでしょうか(ROC曲線のAUCは$0.72$、PR曲線のAUCは$0.47$)。同じデータにも関わらずみる指標によって精度の判断が大きく変わってしまいます。基本は上記の観点でROC曲線とPR曲線を使い分けつつ、タスクに応じて個別で判断することが重要です。
Next
分類以外の機械学習の性能評価についてもまとめていければと思います。