本記事はNTTドコモR&Dアドベントカレンダー15日目の記事です.
こんにちは, NTTドコモ3年目社員の相場(@dcm_aiba)です.
業務ではレコメンド関連の技術開発を行っており,主にPythonやBigqueryを触ってます.
本日は大きく2つ
- 最近流行りのデータドリブンなマーケティングについて
- pythonで1に基づく施策改善を因果推論を使って検討してみた例
を紹介します!
施策評価の進め方について考えるきっかけ作りを目的としており, なるべく難しい言葉や数式は除いています. 専門的な話が知りたい方はぜひ引用先等をご参考下さい.
まだまだ勉強中の身ですので, ぜひ実務で経験された方からご意見ご感想いただけますと幸いです!
それでは早速やっていきましょう!
効果検証において理想的な施策の設計とそうもいかない現実
突然ですが, 効果検証のための理想的な実験設計ってどのようなものでしょうか?
こちらはアドベントカレンダー13日目の記事(*1)で紹介ありましたが, 条件の統制がとれたA/BテストなどのRCT(ランダム化比較試験)が理想ではあるものの, 企業では実施が難しいというのが現状です.
ビジネス観点でも, 打ったら利益が向上するかもしれない施策を一部の人にしか打たないのはもったいないわけですから... (本当にそうかはさておき)

ただ, この後紹介しますが, A/Bテストできない中では往々にして誤った施策評価が行われ, 誤った判断を招いてしまいがちです. その結果, 誤った施策改善が行われサービスの魅力やNPS等の低下に繋がる可能性があります.
その際, 適切なPDCAを回す手段として有効なのが因果推論です.
ここからはどういう意図で因果推論を使うのかといったお話をしていきます.
注)この先はA/Bテストができずに困っている方向けです!!
ぜひ, この先を読む前にA/Bテストが本当にできないのかを考えてみてください. システム改善や周囲の協力次第で可能であれば実現のため奔走いただくのが理想かと思います. 去り際にはぜひLGTM押していただけますと幸いです!←
また, A/Bテストの理想的な実施については個人的にはこちらの記事(*2)や書籍(*3)が参考になりましたのでリンク貼っておきます.
施策による真の持ち上げ効果について
では早速, A/Bテストができない場合の分析について考えてみます.
例えば購買予兆スコアの高い対象者にのみメール配信施策を行った際の購買金額の変化を考えてみると, 結果の捉え方として下記のような分類ができます.
こちらの例は書籍(*3)の例を元に若干改変しております.
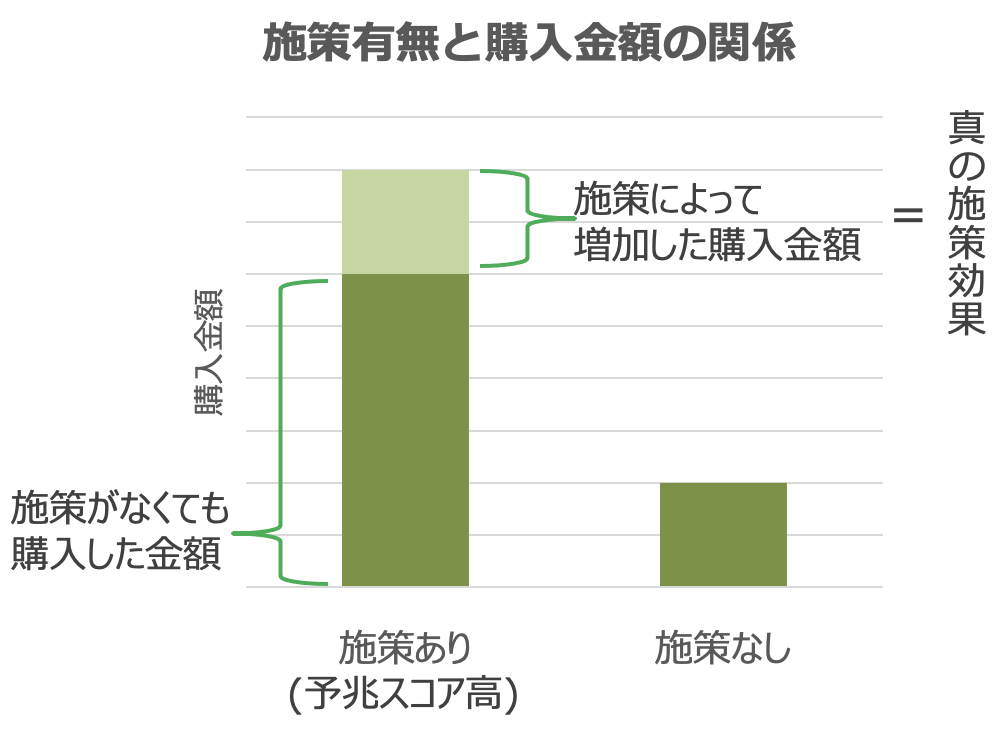
ここで, この施策対象に選ばれるような予兆スコアの高い人は, 元々購入する金額が高い, 購入頻度が多い等の傾向があるため, 元々買う予定だった分からの増分(=真の持ち上げ効果)を考えると薄緑色の部分しかないことがわかります.
この実際には見えない群別(個人別)のデフォルト値とでも呼ぶものがセレクションバイアスと呼ばれるもので, 分析ではこれを除外し真の持ち上げ効果のみを比較する必要があります.
また, この真の持ち上げ効果を求めるための仕組みは難しくなく, 単に施策ありせばの予測結果-施策なかりせばの予測結果から求めるこを考えます. イメージとしてはこんな感じ.

ここで, 各群に関して施策実施or未実施時の結果しか存在しないため, 施策あり群には施策未実施の際の結果といった, 事実とは逆のパターン(=反実仮想)については特に推論するためのモデルを作る必要があります(基本的には事実側の結果も予測モデルの結果を用います).
反実仮想の推論モデルの作り方
meta-learnerについて
反実仮想の推論モデルの一例を紹介します. meta-learnerというアルゴリズムの一つで, 下記のように施策あり/なし群の結果それぞれのみを用いて, ありせば/なかりせば結果を予測するモデルを学習すればいいという考えです.

この2つのモデルを用いれば個別に予測結果の差分をり真の持ち上げ効果を算出できますが, 前述の通り, 施策ありモデルはセレクションバイアスの影響を受けた結果を予測するモデルになっているため結果の補正が必要です.
そこで, 一般的には「そもそも施策が適用されやすいか」といった個人毎の傾向を別のモデルで学習し, その大きさで割るなどで補正を行います. この個人毎の傾向を傾向スコアと呼び, 分析において非常に大事な役割を担います.
傾向スコアによるセレクションバイアスの補正方法について
最もわかりやすいのはInverse Probability Weighting (IPW) 推定量(*4)という値を用いた補正です.
式は下記の通りで,
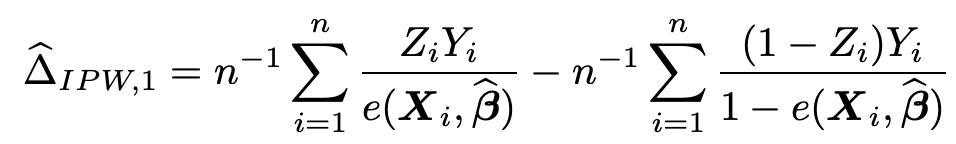
Xは入力特徴量, Yは実際の結果で, Zは施策の有無, e()は(施策ありになりうる)傾向スコアを表しておりありせば確率を, 1-e()は同様になかりせば確率を表します. ただ単純に施策ありの結果, なしの結果を, それらに該当した人のそのようになる傾向の大きさで割っていることがわかります. イメージしやすいですね. ただこちらはあくまで実際の結果のみを用いるので, 個別の反実仮想は算出できません. よって今回はDoubly Robust 推定法という手法(*4)という別の手法を用いることにします.
Doubly Robust 推定法は以下の通りです.
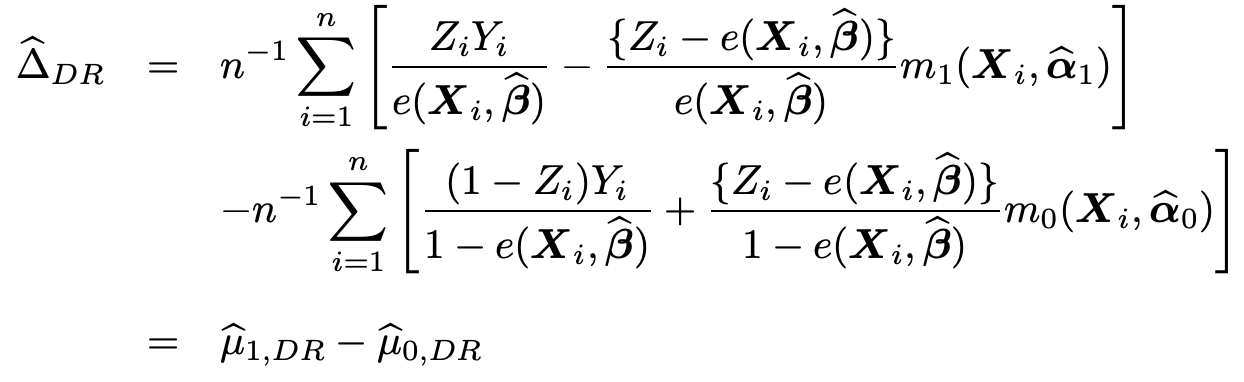
ベースはIPW推定量と同様ですが, m_i()が追加されています. こちら, m_1()は施策ありせば, m_0()はなかりせばモデルの予測結果です. IPW推定量に加えモデル予測結果を併用することで, 傾向スコアの予測誤りに対してもよりロバストな推定結果を導くことができます. 今回はこちらを個人毎に算出します.
その他必要な考慮
また, 使用する特徴量にも注意です. 例えば他にも同時に別のキャンペーンをやっている, そもそも購買価格が高い人であるなど, 施策対象へのなりやすさや施策の結果それぞれに影響しそうな特徴(交絡因子と呼ばれる)をきちんと投入しないと, 反実仮想の正しい推定ができません.
さらには, 苦労して求めたこの真の持ち上げ効果は思ったほど高くはないことが多く(バイアス分を除いているので), 予測モデルの結果であることからも実務上疑念を抱かれることもしばしば...
いかがでしょう? なんだかA/Bテスト実施の方が簡単な気がしてきますね.
ただし, そうもいかない環境で結果を正しく捉えるためにはこういった分析をするしかありません.
もちろん大きなメリットもあります. それは施策改善に活かす材料になるということです.
最後に, この施策改善をどう行うかについて触れた後, 実装に入ります.
施策改善について ~真の持ち上げ効果をどう捉えるか~
ここで, 関連する考え方にuplift modelingというものがあります. この枠組みで考えると非常にわかりやすいので紹介します.
例として, 商品の推薦施策にCVするか否かを考えるとき, uplift modelingでは下記に示す4セグメントに分類します. そして各結果から右のような検討ができます.
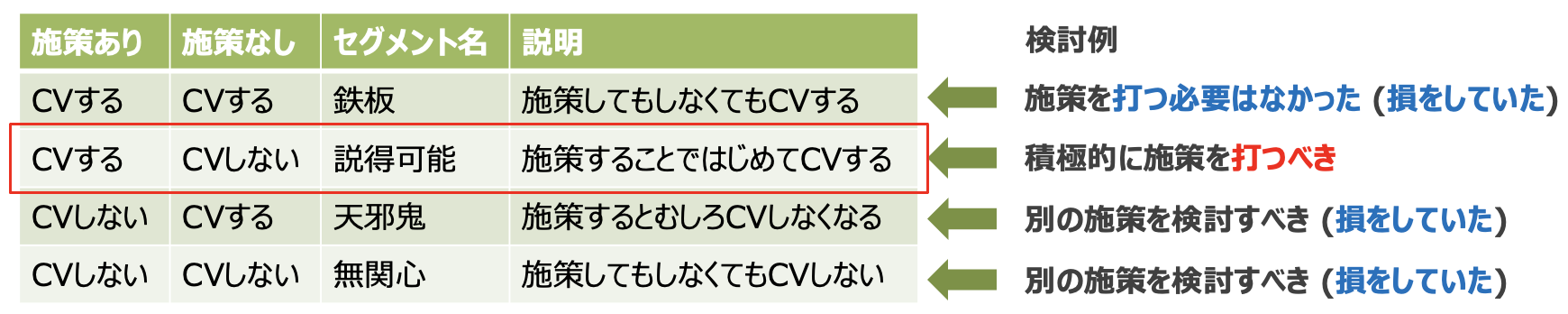
※左表はこちらの記事(*5)から引用.
表のように「鉄板」は施策しなくてもCVしてくれた, 「説得可能」は施策をした意味があった等, 反実仮想を推論することで次に施策を打つべき層や除外すべき層を見出すことができます.
さらに, 真の持ち上げ効果を持ち上げ効果を予測するモデルができれば, 施策効果を受けやすい人の特性などもわかりそうですよね!
適切に反実仮想を推論することは難しいながらもビジネスを回す上で非常に大事な分析になります. では, 実際のデータで試してみましょう!
実際に求めてみる ~Doubly Robust 推定法~
今回はDoubly Robust 推定量を算出しセレクションバイアスを除外したスコアを算出します.
データは岩波データサイエンス Vol.3(*6)のサンプルデータ(*7)を用いています.
こちらは, あるアプリゲームのTVCM視聴有無と, スマートフォンでのアプリゲーム利用情報を同一対象者から得たデータであり, 年齢, 性別, 居住地といった様々な属性データ, TV視聴時間等の行動データと紐づけられています.
データの特徴として,
- ゲームのCM未視聴者はCM視聴者より平均のゲーム利用時間が短い.
といったものがあります. 一見CMによって負の効果があるように見えますが, CM視聴者はそもそもTV視聴時間等のセレクションバイアスがかかっているためです.
本記事ではセレクションバイアスを除外しCM視聴がゲーム利用時間に与える効果, その結果の活用方法を考えます. あくまで流れを理解するという目的で簡単なコードで進めますのでご了承下さい.
より正確に検証する場合は別の記事(*8)が参考になります. 同じデータでより詳しい検証をされています. コードも一部参考にさせていただきました.
# ライブラリインポート
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression, Ridge
import lightgbm as lgb
import shap
import seaborn as sns
import matplotlib.pyplot as plt
import warnings
warnings.simplefilter('ignore')
# サンプルデータの取得
df = pd.read_csv('https://raw.githubusercontent.com/iwanami-datascience/vol3/master/kato%26hoshino/q_data_x.csv')
# x_cols : 学習特徴量(目的変数相当の特徴量を削ります)
# treatment_col : 介入有無(今回はCM視聴)
# y_col : 施策結果(目的変数,利用回数など:今回はゲーム利用時間)
x_cols = [col for col in df.columns \
if col not in ['gamecount', 'gamedummy', 'gamesecond', 'cm_dummy']]
treatment_col = 'cm_dummy'
y_col = 'gamesecond'
続いてDoubly Robust 推定量の算出に必要な
- 施策ありせばモデル
- 施策なかりせばモデル
- 傾向スコア算出モデル
を学習します. 実際には交差検証等を行い精度向上を目指して下さい. 今回の傾向スコア算出モデルはAUC0.78でした. 0.8が望ましいとのこと.
# データ分割
# 一部を評価用にとっておく(評価部分は割愛)
train_data, test_data = train_test_split(df, test_size=0.2, random_state=1)
# train_dataを2群に分ける
# 介入を受けた(=CM視聴)集団(=介入群)
df_1 = train_data[train_data[treatment_col] == 1.0]
# 介入を受けていない(=CM未視聴)集団(=対照群)
df_0 = train_data[train_data[treatment_col] == 0.0]
# モデル学習
# M_g : 傾向スコア算出モデル(学習用全データで介入(ここではCM視聴)傾向を学習)
M_g = Ridge().fit(train_data[x_cols], train_data[treatment_col])
# M_1 : 介入ありせば結果予測モデル(介入群のみで学習)
# M_0 : 介入なかりせば結果予測モデル(対照群のみで学習)
M_1 = LogisticRegression().fit(df_1[x_cols], df_1[y_col])
M_0 = LogisticRegression().fit(df_0[x_cols], df_0[y_col])
準備ができたのでいよいよDoubly Robust 推定量を求めます. ここで, 個別のDoubly Robust 推定量は, ある属性に対する真の施策効果を推定したものになるので, 一般に条件付き平均処置効果(Conditional Average Treatment Effect, CATE)と呼ばれます. 以降CATEと呼びます.
# Doubly Robust 推定量の算出
# 介入群の条件付き平均処置効果
Y_1 = df_1[y_col] / M_g.predict(df_1[x_cols]) \
- M_1.predict(df_1[x_cols]) * (1 - M_g.predict(df_1[x_cols])) / M_g.predict(df_1[x_cols])
Y_0 = M_0.predict(df_1[x_cols])
df_1["CATE"] = Y_1 - Y_0 # ありせば-なかりせばで介入群の推定個別処置効果を推定
# 対照群の条件付き平均処置効果
Y_1 = M_1.predict(df_0[x_cols])
Y_0 = df_0[y_col] / (1 - M_g.predict(df_0[x_cols])) \
- M_0.predict(df_0[x_cols]) * (M_g.predict(df_0[x_cols])) / (1 - M_g.predict(df_0[x_cols]))
df_0["CATE"] = Y_1 - Y_0 # ありせば-なかりせばで対照群の推定個別処置効果を推定
# 交差検証もしていないので外れ値等の誤差が...
print(df_0['CATE'].mean(), df_1['CATE'].mean())
# (9798.658486929771, -4787.006727540364)
# 介入群と対照群の予測結果のdfを結合する
df_DR = pd.concat([df_0, df_1])
他の方の分析結果と比べると雑にモデリングをしている分やや誤差が大きそうですがひとまずCATEが算出できました.
ここで, このCATEを汎化的に予測するためのモデルを学習します. 今回はlightgbmを使いますが, モデル自体はなんでも大丈夫です.
# CATEを目的変数としてvalidationデータを作成
X_train, X_val, y_train, y_val = train_test_split(df_DR[x_cols], df_DR['CATE'], test_size=0.2, random_state=100)
lgb_train = lgb.Dataset(X_train, y_train)
lgb_val = lgb.Dataset(X_val, y_val, reference=lgb_train)
# パラメータの設定
params = {'task': 'train',
'boosting_type': 'gbdt',
'objective': 'regression',
'metric': 'rmse',
'learning_rate': 0.1 }
# CATE予測モデルの学習
M_DR = lgb.train(params,
lgb_train,
num_boost_round=1000,
valid_names=['train', 'valid'],
valid_sets=[lgb_train, lgb_val],
evals_result=evaluation_results,
early_stopping_rounds=30,
verbose_eval=0)
# CATE予測モデルを用いて全対象者のCATEを予測
df['pred_CATE'] = M_DR.predict(df[x_cols])
これにより, 施策に関係ないデータもCATEを予測することができるようになりました!(精度はさておき)
結果の活用
ここから結果の活用に入ります.
まずは, 次に施策を打つべき対象を考えてみます. 本当に施策を打つべきは, 施策なかりせば時かたありせば時の持ち上げ効果の値が高い「説得可能」層です.
今回は個別の持ち上げ効果(=CATE)順に並べ替えて上位1000人のみが施策を受けた場合の群毎の平均の施策効果を考えてみます. ここで, 注目する群全体に対する真の効果はその群平均をもって, 平均処置効果(Average Treatment Effect, ATE)と呼ばれます.
※CATE上位と下位に大きな外れ値があったため上下1%を除外して表示しています.
# CATE上位1000人のみのレコードを表示用dfに再度追加
df_tmp = df.sort_values(['pred_CATE'], ascending=False).head(1000)
df_tmp[treatment_col] = 2
df_next = pd.concat([df, df_tmp],axis=0)
# 外れ値を除外
p99_value = df_next["pred_CATE"].quantile(0.99)
p01_value = df_next["pred_CATE"].quantile(0.01)
df_next = df_next[(df_next["pred_CATE"]<=p99_value)&(df_next["pred_CATE"]>=p01_value)]
font='IPAGothic'
fig = plt.figure(figsize=(7, 7))
ax = fig.add_subplot(1, 1, 1)
ax = sns.barplot(x='cm_dummy', y='pred_CATE', data=df_next, ax=ax, palette="Blues")
ax.set_xticklabels(['CM未視聴', 'CM視聴', '次回の対象候補者'], fontproperties=font)
ax.set_xlabel('')
ax.set_ylabel('CATE平均(持ち上げゲーム利用時間)[秒]', fontproperties=font)
fig.show()

ここで,
- CM未視聴者よりもCM視聴者の方がCM視聴時の持ち上げ効果が高い
- 仮にCATE上位1,000人のみに施策を打つと持ち上げ効果は9,000秒になり現状のCM視聴者よりも約7,000秒長くなる
ことがわかります.
まず1に関してはCMをみてくれる層にきちんと効果あったことを示す結果で, 施策を行ってよかったことがわかります(ビジネスサイドは安心しますね). また, 「CMの費用対効果」という場合にはCM視聴者のみのATEを用いて問題ありません. CMを見た場合の効果なので. ここでは約2,000秒です.
2に関しては本事例だとわかりにくいですが, 仮にメール施策等の場合は次に施策打つ層をCATEの上位層にすると, 施策効果が大きく変わることを示すものになります. 施策の改善案を示すときに使えそうですね! 実はこちらはUplift modelingの文脈でより詳細に分析できるので詳しくは別記事(*5)をご参照下さい.
続いて, モデルの変数重要度やSHAPなどをみていきます.
# 変数重要度を取得
lgb_imp = M_DR.feature_importance(importance_type='gain')
df_importance = pd.DataFrame({'feature':x_cols, 'importance':lgb_imp})
# 変数重要度(上位10件)の表示
plt.figure(figsize=(7, 7))
sns.barplot(
x="importance",
y="feature",
data=df_importance.sort_values('importance', ascending=False).head(10),
palette="Blues_r")
plt.tight_layout()

TV視聴日数や課金額はCATEの予測に大きく関わっていそうですね.
# SHAP値の取得
DR_explainer = shap.TreeExplainer(M_DR, data=df[x_cols])
DR_shap_values = DR_explainer.shap_values(df[x_cols])
# SHAP値の表示
shap.summary_plot(shap_values=DR_shap_values,
features=df[x_cols],
feature_names=x_cols,
max_display=10)

例としてSHAPも簡単に出してみましたが, 年齢は低い方が, 京阪神エリア居住だと効果高そうといったこともわかりますね.
CATE予測モデルを作ることで, 次施策を打つべき対象や, 真に効果を受けやすい属性等が見え, 改善に繋がりそうです!
おわりに
いかがだったでしょうか?
繰り返しになりますが因果推論で分析を行う大きなメリットはセレクションバイアスの除去です.
本ページのコードのように交差検証をしていない, 十分な精度があることを確認しないで取り組むと往々にして誤った解釈を招きかねません.
モデルの結果が全てである因果推論において, 予測結果の正しさは重要です.
さらに, N歳以上の人のみに施策を打つ等, 施策対象とそうでない集団の属性が全く異なる場合にはモデルがうまく学習できず, 傾向スコアだけでは補正できない場合もあります. 与える特徴量も, 交絡因子と呼ばれるものを考慮していないとただ他キャンペーンの影響を大きく受けた予測になってしまったり...
あくまで最終的にはCATEを正しいとみなして議論することになるため, 大前提としてCATEが正しい必要があるのです(そりゃそうだ).
この記事で興味を持たれた方は文献や書籍等で詳しく調べていただくのがよろしいかと思います.
反対に, 大変そうだと思われた方, ぜひ元からバイアスの少ないA/Bテスト実施を目指しましょう!!! (切実)
最後まで読んでいただきありがとうございました.
参考文献
- *1 ノーベル経済学賞から学ぶA/Bテストできない場合の効果検証/@dcm_tzkm
- *2 あなたはA/Bテストを理解しているか?/usaito
- *3 効果検証入門〜正しい比較のための因果推論/計量経済学の基礎
-
*4 Double Robustness in Estimation
of Causal Treatment Effects資料より式引用 (Based in part on Lunceford, J.K. and Davidian, M. (2004). Stratification and
weighting via the propensity score in estimation of causal treatment effects: A
comparative study. Statistics in Medicine 23:2937–2960) - *5 Python で Uplift modeling/0NE_shoT_
- *6 岩波データサイエンス Vol.3
- *7 https://github.com/iwanami-datascience/vol3
- *8 下町データサイエンティストの日常/傾向スコアを用いた因果推論入門~実装編~