はじめに
Uplift modeling は、マーケティング施策によって利益を最大化するための手法です。利益がより大きい顧客にターゲットを絞って、メール送付や広告配信などの施策を打つことで、マーケティングの効率化が実現できます。
この記事では、Uplift modeling の概要と、それを実現するための実装例を備忘録としてまとめます。
Uplift modeling
概要
**Uplift modelingは、ある属性を持つ顧客の、施策実施による利益の増加分(施策を実施した場合の利益と実施しない場合の利益の差分)を予測する方法です。**通常の機械学習による予測タスクでは、施策に対して単純にどう反応するか(予約するか/しないか、予約金額はいくらか、など)を予測しますが、Uplift modelingでは、施策に対して反応がどう変化するか(予約確率や予約金額がどう変化するか)を予測します。顧客の施策に対する反応がどう変化するかを明らかにすることで、効果が高い顧客にのみ施策を実施するターゲッティングや、各顧客に適したマーケティング施策を実施するパーソナライゼーションが可能になります。Uplift modeling で予測されるものは、顧客の属性を条件づけたとき(つまり、同質な属性を持つ顧客)の、施策実施による利益の増加分とも言い換えられるので、CATE (Conditional Average Treatment Effect)、ITE(Indivisual Treatment Effect)とも呼ばれます。
Uplift modeling における顧客の分類
Uplift modeling の枠組みでは、介入(施策の実施)に対してどう反応する(クリックや予約などのコンバージョン(CV)をする)かによって、顧客を4つのセグメントに分類して考えます。
| 介入あり | 介入なし | セグメント名 | 説明 |
|---|---|---|---|
| CVする | CVする | 鉄板 | 介入してもしなくてもCVする |
| CVする | CVしない | 説得可能 | 介入することではじめてCVする |
| CVしない | CVする | 天邪鬼 | 介入するとむしろCVしなくなる |
| CVしない | CVしない | 無関心 | 介入してもしなくてもCVしない |
鉄板は、介入してもしなくてもCVする顧客層です。介入にコストがかかる場合はコストが無駄になるので介入すべきではありません。例えば、直近の購買履歴があるアクティブユーザーがこの層に該当し、メール配信などによって購買を喚起しなくても購買してくれる場合は、メール配信のコストが無駄になってしまいます。
説得可能は、介入しない場合はCVしませんが、介入することではじめてCVする顧客層です。例えば、購買意欲はあるものの購買に踏み切れないユーザーがこの層に該当し、割引クーポンなどを配信することで、この層に属するユーザーが購買してくれる可能性が高くなります。
天邪鬼は、介入しない場合はCVしますが、介入するとむしろCVしなくなる顧客層です。介入することで利益が減少するため、絶対に介入してはいけない顧客層です。
無関心は、介入してもしなくてもCVしない顧客層です。例えば、直近の購買から長期間が経過している離反・休眠ユーザーがこの層に該当し、メール配信をしても購買が見込めない場合は、メール配信をやめることでコストを削減することができます。
Uplift modeling は、説得可能に属する顧客層を見極め、これらの顧客を対象に施策を実施することで、効率的なマーケティングを実現します。
Uplift modeling の主なアルゴリズム
Uplift modelingには、主に2つのアルゴリズムがあります。1つは、Meta-Learner アルゴリズムと呼ばれ、介入する場合の利益と介入しない場合の利益を予測するモデル(base-learner と呼びます)を構築し、利益の増加分を推定するアルゴリズムです。もう1つは、Uplift Tree と呼ばれ、「利益の増加分が大きくなるか?」という基準で、顧客の集団を分割する木を構築するアルゴリズムです。
Meta-Learner アルゴリズム
Meta-Learner アルゴリズムには、介入する場合の利益と介入しない場合の利益をどう予測するかによって、さらに T-Learner, S-Learner, X-Learner, R-Learner などのアルゴリズムに分類されます。
T-Learner
介入する場合の利益の予測するモデルと、介入しない場合の利益を予測するモデルを別個に構築し、それぞれの予測値の差分をとることで、利益の増加分を予測するアルゴリズムです。介入する場合と介入しない場合を分けてモデルを構築するため、介入有無は特徴量として採用しません。
式で書くと、
\mu_1(x) = E(Y_1 | X=x)
\mu_0(x) = E(Y_0 | X=x)
\hat{\tau}(x) = \hat{\mu}_1(x) - \hat{\mu}_0(x)
です。
顧客の背景情報 $x$(デモグラフィック属性や購買履歴など)を特徴量として、介入する場合の利益(予約確率、予約金額など) $Y_1$ を予測するモデルと、介入しない場合の利益 $Y_0$ を予測するモデルを構築し、それらの予測値 $\hat{\mu}_1(x), \hat{\mu}_0(x)$ の差分が、利益の増加分 $\hat{\tau}(x)$ となります。
S-Learner
利益を予測するモデルを1つ構築し、介入する場合と介入しない場合の利益を予測し、それらの差分をとることで、利益の増加分を予測するアルゴリズムです。T-Learner と異なり、介入有無を特徴量として採用します。
式で書くと、
\mu(x, z) = E(Y | X=x, Z=z)
\hat{\tau}(x) = \hat{\mu}(x, Z=1) - \hat{\mu}(x, Z=0)
です。
顧客の背景情報 $x$ と、介入有無を表す群別変数 $z$($z=1$ は介入あり、$z=0$ を表す)を特徴量として、利益 $Y$ を予測するモデルを構築し、介入する場合の予測値 $\hat{\mu}(x, Z=1)$ と介入しない場合の予測値 $\hat{\mu}(x, Z=0)$ の差分が、利益の増加分 $\hat{\tau}(x)$ となります。
X-Learner
介入する場合と介入しない場合の pseudo-effects(疑似的な利益の増加分)をそれぞれ推定し、それらを重み付けをして足し合わせることで、利益の増加分を予測するアルゴリズムです。
X-Learner は、まず顧客の背景情報 $x$ を特徴量として、介入する場合の利益 $Y_1$ を予測するモデルと、介入しない場合の利益 $Y_0$ を予測するモデルを構築します。
\mu_1(x) = E(Y_1 | X=x)
\mu_0(x) = E(Y_0 | X=x)
そして、介入する場合と介入しない場合の pseudo-effects を以下の式で推定します。
D_i^1 = Y_i^1 - \hat{\mu}_0(x_i^1)
D_i^0 = \hat{\mu}_1(x_i^0) - Y_i^0
上付き数字は、1は介入した顧客に紐づくデータ、0は介入していない顧客に紐づくデータを利用することを示します。$D_i^1$ は、介入した顧客から得られた利益 $Y_i^1$ と、介入した顧客に仮に介入しなかった場合の利益 $\hat{\mu}_0(x_i^1)$ の差分であり、介入する顧客グループにおける疑似的な利益の増加分を表します。$D_i^0$ は、介入しなかった顧客に仮に介入した場合の利益 $\hat{\mu}_1(x_i^0)$ と、介入しなかった顧客から得られた利益 $Y_i^0$ の差分であり、介入しない顧客における疑似的な利益の増加分を表します。
さらに、顧客の背景情報 $x$ から、pseudo-effects $D_1, D_2$ を予測するモデルを構築します。
\tau_1(x) = E(D_1 | X=x)
\tau_0(x) = E(D_0 | X=x)
最後に、介入する場合の予測値 $\hat{\tau}_0(x)$ と介入しない場合の予測値 $\hat{\tau}_1(x)$ を $g(x)$ で重みを付けて平均をとり、利益の増加分 $\hat{\tau}(x)$ を予測しています。$g(x)$ の値域は $g(x) \in [0,1]$ で、$g(x)$ としては傾向スコア $e(x)=P(Z=1 | X=x)$ を利用することもできます。
\hat{\tau}(x) = g(x)\hat{\tau}_0(x)+(1-g(x))\hat{\tau}_1(x)
R-Learner
R-Learner は、それぞれの顧客から得られる平均的な利益 $m(x)$ と傾向スコア(=顧客が介入される確率)$e(x)$ を予測し、利益の増加分の予測誤差を最小化するアルゴリズムです。
R-Learner は、まず顧客の背景情報 $x$ を特徴量とし、平均的な利益 $m(x)$、傾向スコア $e(x)$ を予測するモデルを構築します。
m(x) = E(Y | X=x)
e(x) = P(Z=1 | X=x)
そして、利益の増加分の予測誤差(損失関数)$\hat{L}_n(\tau(・))$ が最小になるような、利益の増加分 $\tau(・)$ を求めます。
\hat{\tau}(・) = argmin_{\tau}\{\hat{L}_n(\tau(・)) + \Lambda_n(\tau(・))\}
\hat{L_n(\tau(・))} = \frac{1}{n}\sum_{i=1}^n((Y_i-\hat{m}^{(-i)}(x_i))-(z_i-\hat{e}^{(-i)}(x_i))\tau(x_i))^2
$\Lambda_n(\tau(・))$ は正則化項です。$\hat{m}^{(-i)}(x_i), \hat{e}^{(-i)}(x_i)$ は、顧客 $i$ のデータ以外のデータで構築したモデルで予測した、顧客 $i$ の平均的な利益と傾向スコアを表します。
Uplift Tree
Uplift Tree は、「利益の増加分が大きくなるか?」という基準で、顧客の集団を分割する木を構築するアルゴリズムです。二値分類タスクで用いられる決定木では、分割後の集団におけるクラスの不純度が、分割前に比べて減少するように、ある属性に関する条件で集団を分割します。一方、Uplift Tree では、分割後の集団における、介入ありグループの利益の分布と介入なしグループの利益の分布の距離が、分割前に比べて増加するように、ある属性に関する条件で集団を分割します。つまり、利益の増加に関連が強い属性で顧客集団を分割していきます。
式で書くと、
D_{gain} = D_{after-split}(P^T, P^C) - D_{before-split}(P^T, P^C)
で定義される $D_{gain}$ が大きくなるように木を構築していきます。$P^T, P^C$ は、それぞれ介入ありグループと介入なしグループにおける利益の分布を表し、$D$ は分布の距離を表します。$D$ としては、カルバック・ライブラー情報量や、ユークリッド距離が用いられます。
Uplift modeling の評価指標
Uplift modeling の性能は、**AUUC(Area Under the Uplift Curve)**という指標を用いて評価します。AUUC は、ランダムに選択した顧客に介入する場合と比較して、Uplift moeling で予測した利益の増加分が大きい顧客にのみ介入する場合、どの程度利益が増加するかを正規化した指標です。AUUCの値が大きいほど、Uplift modeling の性能が高いといえます。AUUC を算出する手順は以下の通りです。
- Uplift modeling により予測した利益の増加分が大きいほど大きな値をとるように、それぞれの顧客をスコアリングします。ここでは、このスコアを uplift score と呼びます。(利益としてCVRなどの割合を用いている場合、CVR の増加分をそのまま uplift score として利用できます。)
- uplift score が閾値以上をとる顧客にのみ介入した場合、介入しなかった場合と比較してどれだけ利益が増加したか(ここでは、この値を lift と呼びます)を算出します。
- 2.で介入する顧客と同数の顧客をランダムに選択し介入した場合の利益の増加分と比較して、2.で求めた lift はどの程度増加するかを算出します。
- 2., 3. を閾値を変化させて繰り返し算出した lift を足し合わせ、最後に正規化します。(閾値を変化させて得られる lift をプロットした曲線を uplift curve と呼びます。)
式で書くと、
AUUC = \sum_{k=1}^n AUUC_{\pi}(k)
AUUC_{\pi}(k) = AUL_{\pi}^T(k) - AUL_{\pi}^C(k) = \sum_{i=1}^k (R_{\pi}^T(i) - R_{\pi}^C(i)) - \frac{k}{2}(\bar{R}^T(k) - \bar{R}^C(k))
です。$n$ は全顧客数、$k$ は uplift score が閾値以上となる顧客数、$\pi$ は顧客の順序(uplift socre が大きい順)を表します。$AUL_{\pi}^T(k)$ は、順序 $\pi$ にしたがって $k$ 番目までの顧客に介入した場合の lift、$AUL_{\pi}^C(k)$ は、ランダムに $k$ 人の顧客を選択して介入した場合の利益の増加分です。$R_{\pi}^T(i)$ は、順序 $\pi$ における $i$ 番目の顧客に介入した場合の利益、$R_{\pi}^C(i))$ は、順序 $\pi$ における $i$ 番目の顧客に介入しなかった場合の利益です。$\bar{R}^T(k)$ は、ランダムに選択した $k$ 人に介入した場合の利益、$\bar{R}^C(k)$ は、ランダムに選択した $k$ 人に介入しなかった場合の利益です。$AUL_{\pi}^C(k)$は、底辺 $k$、高さ $\bar{R}^T(k) - \bar{R}^C(k)$ の三角形の面積と見做すこともできます。
実装例
Python で Uplift modeling により利益の増加分を予測するコードを実装します。ここでは、T-Learner, S-Learner を実装しています。なお、ここでの実装は仕事ではじめる機械学習の9章を参考にしています。また、実行環境は、Python 3.7.6, numpy 1.18.1, pandas 1.0.2, scikit-learn 0.22.2 です。以下、コードです。
- 必要なライブラリの読み込み
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
sns.set_style('whitegrid')
import random
from sklearn.linear_model import LogisticRegression
- 利用するデータの生成
ここでの利益は CVR としています。
def generate_sample_data(num, seed=0):
cv_flg_list = [] # コンバージョンしたかを表すフラグのリスト
treat_flg_list = [] # 介入したかを表すフラグのリスト
feature_vector_list = [] # 特徴量のリスト
feature_num = 8 # 特徴量の数
base_weight = [0.02, 0.03, 0.05, -0.04, 0.00, 0.00, 0.00, 0.00] # 特徴量のベース
lift_weight = [0.00, 0.00, 0.00, 0.05, -0.05, 0.00, 0.0, 0.00] # 介入時の特徴量の変化量
random_instance = random.Random(seed)
for i in range(num):
feature_vector = [random_instance.random() for n in range(feature_num)] # 特徴量をランダムに生成
treat_flg = random_instance.choice((1, 0)) # 介入フラグをランダムに生成
cv_rate = sum([feature_vector[n]*base_weight[n] for n in range(feature_num)]) # CVRのベースとなる値を生成
if treat_flg == 1:
cv_rate += sum([feature_vector[n]*lift_weight[n] for n in range(feature_num)]) # 介入するならlift_weightを加味してCVRを加算
cv_flg = 1 if cv_rate > random_instance.random() else 0
cv_flg_list.append(cv_flg)
treat_flg_list.append(treat_flg)
feature_vector_list.append(feature_vector)
df = pd.DataFrame(np.c_[cv_flg_list, treat_flg_list, feature_vector_list],
columns=['cv_flg', 'treat_flg','feature0', 'feature1', 'feature2',
'feature3', 'feature4', 'feature5', 'feature6', 'feature7'])
return df
train_data = generate_sample_data(num=10000, seed=0) # モデル構築用データ(学習データ)
test_data = generate_sample_data(num=10000, seed=1) # モデル性能評価用データ(検証データ)
- T-Learner の実装
# 介入する場合の利益(CVR)を予測するモデル用のデータを用意
X_train_treat = train_data[train_data['treat_flg']==1].drop(['cv_flg', 'treat_flg'], axis=1)
Y_train_treat = train_data.loc[train_data['treat_flg']==1, 'cv_flg']
# 介入しない場合の利益(CVR)を予測するモデル用のデータを用意
X_train_control = train_data[train_data['treat_flg']==0].drop(['cv_flg', 'treat_flg'], axis=1)
Y_train_control = train_data.loc[train_data['treat_flg']==0, 'cv_flg']
# 2つのモデルを構築
treat_model = LogisticRegression(C=0.01, random_state=0)
control_model = LogisticRegression(C=0.01, random_state=0)
treat_model.fit(X_train_treat, Y_train_treat)
control_model.fit(X_train_control, Y_train_control)
# 検証データに対して CVR を予測
X_test = test_data.drop(['cv_flg', 'treat_flg'], axis=1)
treat_score = treat_model.predict_proba(X_test)[:, 1]
control_score = control_model.predict_proba(X_test)[:, 1]
# uplift score を算出
uplift_score = treat_score - control_score
- AUUC の算出
# uplift score が大きい順に検証データを並び替え
result = pd.DataFrame(np.c_[test_data['cv_flg'], test_data['treat_flg'], uplift_score], columns=['cv_flg', 'treat_flg', 'uplift_score'])
result = result.sort_values(by='uplift_score', ascending=False).reset_index(drop=True)
# lift の算出
result['treat_num_cumsum'] = result['treat_flg'].cumsum()
result['control_num_cumsum'] = (1 - result['treat_flg']).cumsum()
result['treat_cv_cumsum'] = (result['treat_flg'] * result['cv_flg']).cumsum()
result['control_cv_cumsum'] = ((1 - result['treat_flg']) * result['cv_flg']).cumsum()
result['treat_cvr'] = (result['treat_cv_cumsum'] / result['treat_num_cumsum']).fillna(0)
result['control_cvr'] = (result['control_cv_cumsum'] / result['control_num_cumsum']).fillna(0)
result['lift'] = (result['treat_cvr'] - result['control_cvr']) * result['treat_num_cumsum']
result['base_line'] = result.index * result['lift'][len(result.index) - 1] / len(result.index)
# AUUC の算出
auuc = (result['lift'] - result['base_line']).sum() / len(result['lift'])
print('AUUC = {:.2f}'.format(auuc))
# 出力:=> AUUC = 37.70
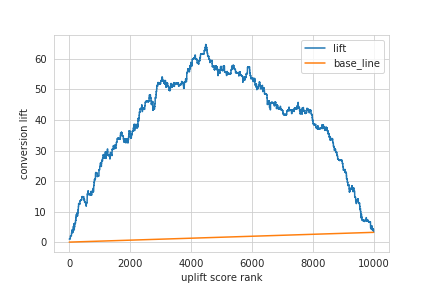
- uplift curve の描画
result.plot(y=['lift', 'base_line'])
plt.xlabel('uplift score rank')
plt.ylabel('conversion lift')
plt.show()
- S-Learner の実装
# 学習データの用意(介入有無と特徴量の交互作用項を作成)
X_train = train_data.drop('cv_flg', axis=1)
for feature in ['feature'+str(i) for i in range(8)]:
X_train['treat_flg_x_' + feature] = X_train['treat_flg'] * X_train[feature]
Y_train = train_data['cv_flg']
# モデルを構築
model = LogisticRegression(C=0.01, random_state=0)
model.fit(X_train, Y_train)
# 介入する場合の検証データの用意
X_test_treat = test_data.drop('cv_flg', axis=1).copy()
X_test_treat['treat_flg'] = 1
for feature in ['feature'+str(i) for i in range(8)]:
X_test_treat['treat_flg_x_' + feature] = X_test_treat['treat_flg'] * X_test_treat[feature]
# 介入しない場合の検証データの用意
X_test_control = test_data.drop('cv_flg', axis=1).copy()
X_test_control['treat_flg'] = 0
for feature in ['feature'+str(i) for i in range(8)]:
X_test_control['treat_flg_x_' + feature] = X_test_control['treat_flg'] * X_test_control[feature]
# 検証データに対して利益 CVR を予測
treat_score = model.predict_proba(X_test_treat)[:, 1]
control_score = model.predict_proba(X_test_control)[:, 1]
# uplift score の算出
uplift_score = treat_score - control_score
T-Learner と同様に AUUC を評価したところ、AUUC = 19.60となり、今回のデータでは T-Learner のほうが性能が高いという結果になりました。
おわりに
Uplift modeling の概要と、それを実現するための実装例をまとめました。
誤りなどありましたら編集リクエストをして頂けると幸いです。