Go to Qiita Advent Calendar 2024 Top
LoginSignup
8
9

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 1 year has passed since last update.

@dc1394

有限要素法で、ヘリウム原子に対するHartree-Fock方程式を解いてみる（Juliaでやってみた）

Last updated at Posted at 2021-03-07

この記事では，ヘリウム原子に対するHartree-Fock方程式を有限要素法（Finite Element Method，FEM）で，数値的に解いてみることにします．有限要素法自体については，この記事ではあまり深入りしません（有限要素法自体の解説は，@Sunset_Yuhi様のこちらの記事や，参考文献1，参考文献2などが分かりやすいのではないかと思います）．

ヘリウム原子に対するHartree-Fock方程式

さて，早速ですが，ヘリウム原子に対するHartree-Fock方程式は，Hartree原子単位系で（以下，断りなしにHartree原子単位系を用いることとします），

\left(  -\dfrac{1}{2}\nabla^{2}-\dfrac{2}{r_{1}}+%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
d\vec{r}_{2}\left\vert \phi\left(  \vec{r}_{2}\right)  \right\vert ^{2}%
\dfrac{1}{\left\vert \vec{r}_{1}-\vec{r}_{2}\right\vert }\right)  \phi\left(
\vec{r}_{1}\right)  dr=E^{\prime}\phi\left(  \vec{r}_{1}\right) \tag{1}

となります（この導出についてはこちらの記事をご覧ください）．ここで，興味があるのはヘリウム原子の基底状態のみであり，球対称条件が使えるので，水素原子のSchrödinger方程式を有限要素法で解いたときの記事と同じ論法が使え，ヘリウム原子に対するHartree-Fock方程式は，

\left(  -\dfrac{1}{2}\dfrac{d^{2}}{dr^{2}}-\dfrac{1}{r}\dfrac{d}{dr}%
-\dfrac{2}{r}+%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
d\vec{r}_{2}\left\vert \phi\left(  \vec{r}_{2}\right)  \right\vert ^{2}%
\dfrac{1}{\left\vert \vec{r}_{1}-\vec{r}_{2}\right\vert }\right)  \phi\left(
r\right)  dr=E^{\prime}\phi\left(  r\right) \tag{2}

となります（左辺第四項を除いて，1次元の問題になったので，添字も省略しました）．ここで，まず$ (2) $式の左辺第四項を無視します．すると，

\left(  -\dfrac{1}{2}\dfrac{d^{2}}{dr^{2}}-\dfrac{1}{r}\dfrac{d}{dr}%
-\dfrac{2}{r}\right)  \phi\left(  r\right)  dr=E^{\prime}\phi\left(  r\right) \tag{3}

が得られます．まずは，水素原子のSchrödinger方程式を有限要素法で解いたときと同様に，$ (3) $式を弱形式にしてみることにします．

(3)式を弱形式にする

水素原子のSchrödinger方程式を有限要素法で解いたときと同様な方法で，$ (3) $式を弱形式にしてみると（詳細は水素原子のときと全く同じなので割愛します），

%
%TCIMACRO{\dint \nolimits_{0}^{r_{c}}}%
%BeginExpansion
{\displaystyle\int\nolimits_{0}^{r_{c}}}
%EndExpansion
\left[  \dfrac{r^{2}}{2}\dfrac{d\phi^{\ast}\left(  r\right)  }{dr}\dfrac
{d\phi\left(  r\right)  }{dr}-2r\phi^{\ast}\left(  r\right)  \phi\left(
r\right)  \right]  dr=E^{\prime}%
%TCIMACRO{\dint \nolimits_{0}^{r_{c}}}%
%BeginExpansion
{\displaystyle\int\nolimits_{0}^{r_{c}}}
%EndExpansion
r^{2}\phi^{\ast}\left(  r\right)  \phi\left(  r\right)  dr \tag{4}

が得られます（この計算は，こちらを参照してください）．ただし，境界条件として，

\phi\left(  r_{c}\right)  =\phi^{\ast}\left(  r_{c}\right)  =0 \tag{5}

を使っていることに注意してください．

HartreeポテンシャルをPoisson方程式から求める

さて次に，$ (1) $式の左辺第四項を求める方法について考えてみましょう．$ (1) $式の左辺第四項は，波動関数から決まる電荷分布により作られるポテンシャルであり，Hartreeポテンシャルと呼ばれています．Hartreeポテンシャル$ V_{H}( \vec{r}_{1}) $は，$ (1) $式の左辺第四項の通り，

V_{H}\left(  \vec{r}_{1}\right)  =%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
d\vec{r}_{2}\left\vert \phi\left(  \vec{r}_{2}\right)  \right\vert ^{2}%
\dfrac{1}{\left\vert \vec{r}_{1}-\vec{r}_{2}\right\vert } \tag{6}

で定義されますが，定義の通り$ (6) $式の右辺を積分して$ V_{H}(\vec{r}_{1}) $を求めるより，次のPoisson方程式

\nabla^{2}V_{H}\left(  \vec{r}\right)  =-4\pi n\left(  \vec{r}\right) \tag{7}

を用いて求めた方が簡単です（3次元の問題になったので，添字を省略しました）．ここで，

n\left(  \vec{r}\right)  =\left\vert \phi\left(  \vec{r}\right)  \right\vert
^{2} \tag{8}

です．さらにここで，電子密度$ n(\vec{r}) $が球対称であることを用い，

U\left(  r\right)  =rV_{H}\left(  r\right) \tag{9}

と書きます．すると，$ (7) $式は，

\dfrac{d^{2}U\left(  r\right)  }{dr^{2}}=-4\pi rn\left(  r\right) \tag{10}

に帰着します．ここで，$ \phi(r) $を，

%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
r^{2}n\left(  r\right)  dr=%
%TCIMACRO{\dint }%
%BeginExpansion
{\displaystyle\int}
%EndExpansion
r^{2}\left\vert \phi\left(  r\right)  \right\vert ^{2}dr=1 \tag{11}

ととると，電子密度に（角度に関する積分からくる）因子$ 4\pi $が含まれているので，Poisson方程式の因子$ 4\pi $が落ちて，

\dfrac{d^{2}U\left(  r\right)  }{dr^{2}}=-rn\left(  r\right) \tag{12}

となります．ここで，境界条件は，

U\left(  0\right)  =0 \tag{13-1}

U\left(  r_{c}\right)  =1 \tag{13-2}

です．ここで，$ (13-2) $式は，Hartreeポテンシャルはこの場合は遠方で$ 1/r $で減衰し，$ r=r_{c} $では$ U(r) = r \times 1/r = 1 $と見なせることを用いました．

Hartree-Fock方程式について，弱形式からローカル行列を生成する

以上より，ヘリウム原子（の基底状態）に対するHartree-Fock方程式は，

\left(  -\dfrac{1}{2}\dfrac{d^{2}}{dr^{2}}-\dfrac{1}{r}\dfrac{d}{dr}%
-\dfrac{2}{r}+\dfrac{U\left(  r\right)  }{r}\right)  \phi\left(  r\right)
dr=E\phi\left(  r\right) \tag{14}

となります．ここで，$ (14) $式は$ (12) $式との非線形連立常微分方程式になっており，一回では解けません．こちらの記事で，基底で展開した場合と同様に，SCF（自己無撞着）計算によって解かなければなりません．
さて，水素原子のSchrödinger方程式を有限要素法で解いたときと同様に，両辺に$ r^{2} $を掛けて，右辺と左辺の満たす行列方程式およびローカル行列$ \mathbf{A} $と$ \mathbf{B} $の成分を求めると，

\left\langle \phi_{\alpha}^{\left(  e\right)  }\right\vert A_{\alpha\beta
}^{\left(  e\right)  }\left\vert \phi_{\beta}^{\left(  e\right)
}\right\rangle =\left\langle \phi_{\alpha}^{\left(  e\right)  }\right\vert
B_{\alpha\beta}^{\left(  e\right)  }\left\vert \phi_{\beta}^{\left(  e\right)
}\right\rangle \tag{15}

A_{11}^{\left(  e\right)  }=\dfrac{l^{e}}{2}\left(  e^{2}+e+\dfrac{1}
{3}\right)  -\left(  l^{e}\right)  ^{2}\left(  \dfrac{2}{3}e+\dfrac{1}
{6}\right)  +%
%TCIMACRO{\dint _{r_{0}^{e}}^{r_{1}^{e}}}%
%BeginExpansion
{\displaystyle\int_{r_{0}^{e}}^{r_{1}^{e}}}
%EndExpansion
\chi_{1}\left(  r\right)  rU\left(  r\right)  \chi_{1}\left(  r\right) \tag{16-1}

A_{12}^{\left(  e\right)  }=A_{21}^{\left(  e\right)  }=-\dfrac{l^{e}}
{2}\left(  e^{2}+e+\dfrac{1}{3}\right)  -\left(  l^{e}\right)  ^{2}\left(
\dfrac{e}{3}+\dfrac{1}{6}\right)  +%
%TCIMACRO{\dint _{r_{0}^{e}}^{r_{1}^{e}}}%
%BeginExpansion
{\displaystyle\int_{r_{0}^{e}}^{r_{1}^{e}}}
%EndExpansion
\chi_{1}\left(  r\right)  rU\left(  r\right)  \chi_{2}\left(  r\right) \tag{16-2}

A_{22}^{\left(  e\right)  }=\dfrac{l^{e}}{2}\left(  e^{2}+e+\dfrac{1}
{3}\right)  -\left(  l^{e}\right)  ^{2}\left(  \dfrac{2}{3}e+\dfrac{1}
{2}\right)  +%
%TCIMACRO{\dint _{r_{0}^{e}}^{r_{1}^{e}}}%
%BeginExpansion
{\displaystyle\int_{r_{0}^{e}}^{r_{1}^{e}}}
%EndExpansion
\chi_{2}\left(  r\right)  rU\left(  r\right)  \chi_{2}\left(  r\right) \tag{16-3}

B_{11}^{\left(  e\right)  }=\left(  l^{e}\right)  ^{3}\left(  \dfrac{e^{2}%
}{3}+\dfrac{e}{6}+\dfrac{1}{30}\right) \tag{16-4}

B_{12}^{\left(  e\right)  }=B_{21}^{\left(  e\right)  }=\left(  l^{e}\right)
^{3}\left(  \dfrac{e^{2}}{6}+\dfrac{e}{6}+\dfrac{1}{20}\right) \tag{16-5}

B_{22}^{\left(  e\right)  }=\left(  l^{e}\right)  ^{3}\left(  \dfrac{e^{2}%
}{3}+\dfrac{e}{2}+\dfrac{1}{5}\right)  \ \tag{16-6}

となります．ここで，

\chi_{1}\left(  r\right)  =\dfrac{r_{2}^{e}-r}{l_{e}} \tag{17-1}

\chi_{2}\left(  r\right)  =\dfrac{r-r_{1}^{e}}{l_{e}} \tag{17-2}

です．ただし，$ r^e_1, r^e_2 $は$ e $番目の要素をなす2節点の$r$座標，$l^e=r_2^e - r_1^e $は線分要素の長さです．$ (16-1) $～$ (16-6) $式の計算はこちらにあります（ただし，$ (16-1) $～$ (16-3) $式の左辺第三項は，数値積分により求めなければならないので，計算から省いてあります）．

ローカル行列から全体行列を生成し，一般化固有値問題を導く

次に，ローカル行列から全体行列$ \mathbf{H} $と$ \mathbf{U} $が満たす行列方程式を生成し，一般化固有値問題を導きます（詳細は水素原子のときと全く同じなので割愛します）．全体行列$ \mathbf{H} $と$ \mathbf{U} $は以下の関係式を満たします．

\left\langle \Phi_{i}\right\vert H_{ij}\left\vert \Phi_{j}\right\rangle
=\left\langle \Phi_{i}\right\vert U_{ij}\left\vert \Phi_{j}\right\rangle
~~~\left(  i,j=1,\ldots,N\right) \tag{18}

ただし，$ H_{ij} $は，$ N $次正方行列$ \mathbf{H} $の成分，$ U_{ij} $は，$ N $次正方行列$ \mathbf{U} $の成分です．ここで，変分原理を用いると，$ (18) $式から結局，

H_{ij}\left\vert \Phi_{j}\right\rangle =E^{\prime}U_{ij}\left\vert \Phi_{j}%
\right\rangle \tag{19}

なる，一般化固有値問題が得られます．ここで，$ E^{\prime} $は，Hartree-Fock方程式のエネルギー固有値です．

Hartree-Fock方程式の境界条件処理

境界条件は，$ \phi(0) $ = 有限，$ \phi(r_{c}) $ = 0ですが，後者の境界条件処理は簡単で，全体行列$ \mathbf{H} $と$ \mathbf{U} $の，$ N $行目と$ N $列目を削るだけです．前者については，水素原子の場合と同様に，境界条件処理が不要とします．

波動関数を規格化（正規化）する

最後に，波動関数$ \phi(r) $を規格化（正規化）します．具体的には，

%
%TCIMACRO{\dint \nolimits_{0}^{r_{c}}}%
%BeginExpansion
{\displaystyle\int\nolimits_{0}^{r_{c}}}
%EndExpansion
r^{2}\phi^{\ast}\left(  r\right)  \phi\left(  r\right)  dr=1 \tag{20}

が満たされるように，$ \phi(r) $を定数倍します．これは，

A^{2}=%
%TCIMACRO{\dint \nolimits_{0}^{r_{c}}}%
%BeginExpansion
{\displaystyle\int\nolimits_{0}^{r_{c}}}
%EndExpansion
r^{2}\phi^{\ast}\left(  r\right)  \phi\left(  r\right)  dr \tag{21}

\phi\left(  r\right)  :=\dfrac{1}{A}\phi\left(  r\right) \tag{22}

とすることにより可能です．ここで，$ (21) $式は，数値積分によって求めなければなりません．

ヘリウム原子のHartree-Fock方程式を，有限要素法で数値的に解くJuliaのプログラム

上述の方法によって，ヘリウム原子の基底状態に対するHartree-Fock方程式を，有限要素法で数値的に解くJuliaのプログラムは以下のようになります．ただし，全部載せると非常に長くなってしまうので，一部だけを掲載しています．なお，完全なコードはGitHubのこちらで公開しています．

function make_wavefunction(iter, hfem_param, hfem_val, vh_val)
    if iter == 0
        # データの生成
        make_data!(hfem_param, hfem_val)
    
        return nothing
    end

    # 要素行列の生成
    make_element_matrix!(hfem_param, hfem_val, vh_val)

    # 全体行列を生成
    hg_tmp, ug_tmp = make_global_matrix(hfem_param, hfem_val)

    # 境界条件処理を行う
    boundary_conditions!(hfem_param, hfem_val, hg_tmp, ug_tmp)

    # 一般化固有値問題を解く
    eigenval, phi = eigen!(hfem_val.hg, hfem_val.ug)
    
    # 基底状態の固有ベクトルを取り出す
    hfem_val.phi = @view(phi[:,1])

    # 固有ベクトルの要素数を増やす
    resize!(hfem_val.phi, NODE_TOTAL)

    # 端点rcでの値を0にする
    hfem_val.phi[NODE_TOTAL] = 0.0

    # 固有ベクトル（波動関数）を規格化
    normalize!(hfem_val)

    return eigenval[1]
end

function boundary_conditions!(hfem_param, hfem_val, hg_tmp, ug_tmp)
    hfem_val.hg = Symmetric(zeros(hfem_param.ELE_TOTAL, hfem_param.ELE_TOTAL))
    hfem_val.ug = Symmetric(zeros(hfem_param.ELE_TOTAL, hfem_param.ELE_TOTAL))

    @inbounds for i = 1:hfem_param.ELE_TOTAL
        for j = i - 1:i + 1
            if j != 0 && j != hfem_param.NODE_TOTAL
                hfem_val.hg.data[j, i] = hg_tmp.data[j, i]
                hfem_val.ug.data[j, i] = ug_tmp.data[j, i]
            end
        end
    end
end

get_A_matrix_element(e, le, p, q, hfem_param, hfem_val, vh_val) = let
    ed = float(e - 1)
    @match p begin
        1 =>
            @match q begin
                1 => return 0.5 * le * (ed * ed + ed + 1.0 / 3.0) - le * le * (2.0 * ed / 3.0 + 1.0 / 6.0) + 
                            GaussLegendre.gl_integ(r -> r * (hfem_val.node_r_ele[e, 2] - r) / hfem_val.length[e] * rVh(hfem_param, hfem_val, vh_val, r) * (hfem_val.node_r_ele[e, 2] - r) / hfem_val.length[e],
                                                   hfem_val.node_r_ele[e, 1],
                                                   hfem_val.node_r_ele[e, 2],
                                                   vh_val)
                2 => return -0.5 * le * (ed * ed + ed + 1.0 / 3.0) - le * le * (ed / 3.0 + 1.0 / 6.0) +
                            GaussLegendre.gl_integ(r -> r * (hfem_val.node_r_ele[e, 2] - r) / hfem_val.length[e] * rVh(hfem_param, hfem_val, vh_val, r) * (r - hfem_val.node_r_ele[e, 1]) / hfem_val.length[e],
                                                   hfem_val.node_r_ele[e, 1],
                                                   hfem_val.node_r_ele[e, 2],
                                                   vh_val)
                _ => return 0.0
            end

        2 =>
            @match q begin
                2 => return 0.5 * le * (ed * ed + ed + 1.0 / 3.0) - le * le * (2.0 * ed / 3.0 + 0.5) +
                            GaussLegendre.gl_integ(r -> r * (r - hfem_val.node_r_ele[e, 1]) / hfem_val.length[e] * rVh(hfem_param, hfem_val, vh_val, r) * (r - hfem_val.node_r_ele[e, 1]) / hfem_val.length[e],
                                                        hfem_val.node_r_ele[e, 1],
                                                        hfem_val.node_r_ele[e, 2],
                                                        vh_val)
                _ => return 0.0
            end

        _ => return 0.0
    end
end

get_B_matrix_element(e, le, p, q) = let
    ed = float(e - 1)
    @match p begin 
        1 =>
            @match q begin
                1 => return le * le * le * (ed * ed / 3.0 + ed / 6.0 + 1.0 / 30.0)
                2 => return le * le * le * (ed * ed / 6.0 + ed / 6.0 + 0.05)
                _ => return 0.0
            end

        2 =>
            @match q begin
                2 => return le * le * le * (ed * ed / 3.0 + ed / 2.0 + 0.2)
                _ => return 0.0
            end
        
        _ => return 0.0
    end
end

function make_data!(hfem_param, hfem_val)
    # Global節点のx座標を定義(R_MIN～R_MAX）
    dr = (hfem_param.R_MAX - hfem_param.R_MIN) / float(hfem_param.ELE_TOTAL)
    @inbounds for i = 0:hfem_param.NODE_TOTAL - 1
        # 計算領域を等分割
        hfem_val.node_r_glo[i + 1] = hfem_param.R_MIN + float(i) * dr
    end

    @inbounds for e = 1:hfem_param.ELE_TOTAL
        hfem_val.node_num_seg[e, 1] = e
        hfem_val.node_num_seg[e, 2] = e + 1
    end
        
    @inbounds for e = 1:hfem_param.ELE_TOTAL
        for i = 1:2
            hfem_val.node_r_ele[e, i] = hfem_val.node_r_glo[hfem_val.node_num_seg[e, i]]
        end
    end

    # 各線分要素の長さを計算
    @inbounds for e = 1:hfem_param.ELE_TOTAL
        hfem_val.length[e] = abs(hfem_val.node_r_ele[e, 2] - hfem_val.node_r_ele[e, 1])
    end
end

function make_element_matrix!(hfem_param, hfem_val, vh_val)
    # 要素行列の各成分を計算
    @inbounds for e = 1:hfem_param.ELE_TOTAL
        le = hfem_val.length[e]
        for j = 1:2
            for i = 1:j
                hfem_val.mat_A_ele[e, i, j] = get_A_matrix_element(e, le, i, j, hfem_param, hfem_val, vh_val)
                hfem_val.mat_B_ele[e, i, j] = get_B_matrix_element(e, le, i, j)
            end
        end
    end
end

function make_global_matrix(hfem_param, hfem_val)
    hg_tmp = Symmetric(zeros(hfem_param.NODE_TOTAL, hfem_param.NODE_TOTAL))
    ug_tmp = Symmetric(zeros(hfem_param.NODE_TOTAL, hfem_param.NODE_TOTAL))

    @inbounds for e = 1:hfem_param.ELE_TOTAL
        for j = 1:2
            for i = 1:j
                hg_tmp.data[hfem_val.node_num_seg[e, i], hfem_val.node_num_seg[e, j]] += hfem_val.mat_A_ele[e, i, j]
                ug_tmp.data[hfem_val.node_num_seg[e, i], hfem_val.node_num_seg[e, j]] += hfem_val.mat_B_ele[e, i, j]
            end
        end
    end

    return hg_tmp, ug_tmp
end

function normalize!(hfem_val)
    sum = 0.0
    len = length(hfem_val.phi)
    max = len - 2

    # Simpsonの公式によって数値積分する
    @inbounds @simd for i = 1:2:max
        f0 = hfem_val.phi[i] * hfem_val.phi[i] * hfem_val.node_r_glo[i] * hfem_val.node_r_glo[i]
        f1 = hfem_val.phi[i + 1] * hfem_val.phi[i + 1] * hfem_val.node_r_glo[i + 1] * hfem_val.node_r_glo[i + 1]
        f2 = hfem_val.phi[i + 2] * hfem_val.phi[i + 2] * hfem_val.node_r_glo[i + 2] * hfem_val.node_r_glo[i + 2]
        
        sum += (f0 + 4.0 * f1 + f2)
    end
    
    hfem_val.phi = map(x -> abs(x * sqrt(sum * hfem_val.length[1] / 3.0)), hfem_val.phi)
end

ヘリウム原子のPoisson方程式を弱形式にする

次に，$ (12) $式のPoisson方程式を弱形式にして，ローカル行列を生成していきましょう．例のごとく，$ (12) $式の両辺に，左から重み関数$ \omega(r) $を乗じて，全空間で部分積分することにより，弱形式にしていきましょう．ここで，重み関数$ \omega(r) $には，$ U(r) $自身を用います．すると，

%
%TCIMACRO{\dint \nolimits_{0}^{r_{c}}}%
%BeginExpansion
{\displaystyle\int\nolimits_{0}^{r_{c}}}
%EndExpansion
\dfrac{dU\left(  r\right)  }{dr}\dfrac{dU\left(  r\right)  }{dr}dr=%
%TCIMACRO{\dint \nolimits_{0}^{r_{c}}}%
%BeginExpansion
{\displaystyle\int\nolimits_{0}^{r_{c}}}
%EndExpansion
rn\left(  r\right)  U\left(  r\right)  dr \tag{23}

が得られます．この計算は，こちらを参照してください（導出の過程で，境界条件$ (13-1) $～$ (13-3) $式を使っていることに注意してください．

弱形式から要素行列と各要素におけるローカル節点ベクトル（各要素における未知係数ベクトル）を生成する

では，$ (23) $式から要素行列とローカル節点ベクトル（各要素における未知係数ベクトル）を生成していきましょう．$ (23) $式を$ N $個の要素で離散化することにより，

%
%TCIMACRO{\dsum \limits_{e=1}^{N}}%
%BeginExpansion
{\displaystyle\sum\limits_{e=1}^{N}}
%EndExpansion%
%TCIMACRO{\dint \nolimits_{0}^{r_{c}}}%
%BeginExpansion
{\displaystyle\int\nolimits_{0}^{r_{c}}}
%EndExpansion
\dfrac{dU\left(  r\right)  }{dr}\dfrac{dU\left(  r\right)  }{dr}dr=%
%TCIMACRO{\dsum \limits_{e=1}^{N}}%
%BeginExpansion
{\displaystyle\sum\limits_{e=1}^{N}}
%EndExpansion%
%TCIMACRO{\dint \nolimits_{0}^{r_{c}}}%
%BeginExpansion
{\displaystyle\int\nolimits_{0}^{r_{c}}}
%EndExpansion
rn\left(  r\right)  U\left(  r\right)  dr \tag{24}

なる式が得られます．ここで，$ (23) $式に$ (17-1) $式と$ (17-2) $式を代入すると，

\mathbf{A}^{\prime\left(  e\right)  }\vec{u}^{\left(  e\right)  }=\vec
{b}^{\left(  e\right)  } \tag{25}

なる連立方程式（要素方程式）が得られます．ここで，左辺の要素行列$ \mathbf{A}^{(e)} $（$ 2 $次正方行列）の成分は，

A_{ij}^{\left(  e\right)  }=\dfrac{\left(  -1\right)  ^{i}\left(  -1\right)
^{j}}{l^{e}} \tag{26}

であり，右辺のローカル節点ベクトル$ \vec{b}^{(e)} $（$ 2 $行$ 1 $列ベクトル）の成分は，

b_{i}^{\left(  e\right)  }=%
%TCIMACRO{\dint \nolimits_{r_{0}^{e}}^{r_{1}^{e}}}%
%BeginExpansion
{\displaystyle\int\nolimits_{r_{0}^{e}}^{r_{1}^{e}}}
%EndExpansion
rn\left(  r\right)  \chi_{i}^{e}\left(  r\right)  dr \tag{27}

です（この計算は，こちらを参照してください）．ここで，$ (27) $式は数値積分により求めなければなりません．

ローカル行列から係数行列と右辺ベクトルを生成し，連立方程式（全体方程式）を導く

次に，要素行列から係数行列$ \mathbf{A}^{\prime} $（$ N $次正方行列）を生成し，またローカル節点ベクトルから右辺ベクトル$ \vec{b} $（$ N $行$ 1 $列ベクトル）を生成することにしましょう．また，それらが満たす連立方程式（全体方程式）も生成していきましょう．これは，係数行列の対角要素と右辺ベクトル（最初と最後を除く）が隣接する要素からの寄与の合計であることに注意して，要素ごとに$ (25) $式を重ね合わせることで可能です．これにより，以下の連立方程式が得られます．

\mathbf{A}^{\prime}\vec{u}=\vec{b} \tag{28}

Poisson方程式の境界条件処理

次に，$ (28) $式の$ \mathbf{A}^{\prime} $，$ \vec{b} $に境界条件処理を行います．$ (14-1) $式，および$ (14-2) $式は，いわゆるDirichlet境界条件です．
ここで，原点でのDirichlet境界条件処理を行う場合は，$ U(0) = 0 $および$ \mathbf{A}^{\prime} $が三重対角行列であることを利用すると，まず，$ \vec{b} $の$ 1 $行成分を$ 0 $にします．次に，$ \mathbf{A}^{\prime} $の(1, 2)成分と，$ \mathbf{A}^{\prime} $の(2, 1)成分を$ 0 $にした後，最後に$ \mathbf{A}^{\prime} $の(1 , 1)成分を$ 1 $にして完成です．
また，$ r = r_c $でのDirichlet境界条件処理を行う場合は，$ U(r_c) = 1 $および$ \mathbf{A}^{\prime} $が三重対角行列であることを利用すると，まず$ \vec{b} $の$ N $行要素を$ 1 $にし，$ \vec{b} $の$ N - 1 $行要素から$ \mathbf{A}^{\prime} $の(N - 1, N)成分を引きます．さらに，$ \mathbf{A}^{\prime} $の(N - 1, N)成分と，$ \mathbf{A}^{\prime} $の(N, N - 1)成分を$ 0 $にした後，最後に$ \mathbf{A}^{\prime} $の(N , N)成分を$ 1 $にして完成です．

ヘリウム原子のPoisson方程式を，有限要素法で数値的に解くJuliaのプログラム

上述の方法によって，ヘリウム原子のPoisson方程式を，有限要素法で数値的に解くJuliaのプログラムは以下のようになります．ただし，全部載せると非常に長くなってしまうので，一部だけを掲載しています．なお，完全なコードはGitHubのこちらで公開しています．

function solvepoisson!(iter, hfem_param, hfem_val, vh_val)
    @match iter begin
        # 要素行列とLocal節点ベクトルを生成
        0 => make_element_matrix_and_vector_first(hfem_param, hfem_val, vh_val)
    
        # 要素行列とLocal節点ベクトルを生成
        _ => make_element_matrix_and_vector(hfem_param, hfem_val, vh_val)
    end

    # 係数行列と右辺ベクトルを生成
    tmp_dv, tmp_ev = make_global_matrix_and_vector(hfem_param, hfem_val, vh_val)

    # 境界条件処理
    boundary_conditions!(vh_val, hfem_param, tmp_dv, tmp_ev)

    # 連立方程式を解く
    vh_val.ug = vh_val.mat_A_glo \ vh_val.vec_b_glo
end

function boundary_conditions!(vh_val, hfem_param, tmp_dv, tmp_ev)
    a = 0.0
    tmp_dv[1] = 1.0
    vh_val.vec_b_glo[1] = a
    tmp_ev[1] = 0.0

    b = 1.0
    tmp_dv[hfem_param.NODE_TOTAL] = 1.0
    vh_val.vec_b_glo[hfem_param.NODE_TOTAL] = b
    vh_val.vec_b_glo[hfem_param.NODE_TOTAL - 1] -= b * tmp_ev[hfem_param.NODE_TOTAL - 1]
    tmp_ev[hfem_param.NODE_TOTAL - 1] = 0.0

    vh_val.mat_A_glo = SymTridiagonal(tmp_dv, tmp_ev)
end

function make_element_matrix_and_vector(hfem_param, hfem_val, vh_val)
    # 要素行列とLocal節点ベクトルの各成分を計算
    for e = 1:hfem_param.ELE_TOTAL
        for i = 1:2
            for j = 1:2
                vh_val.mat_A_ele[e, i, j] = (-1) ^ i * (-1) ^ j / hfem_val.length[e]
            end

            vh_val.vec_b_ele[e, i] =
                @match i begin
                    1 => GaussLegendre.gl_integ(r -> r * rho(hfem_param, hfem_val, r) * (hfem_val.node_r_ele[e, 2] - r) / hfem_val.length[e],
                                                 hfem_val.node_r_ele[e, 1],
                                                 hfem_val.node_r_ele[e, 2],
                                                 vh_val)
                    
                    2 => GaussLegendre.gl_integ(r -> r * rho(hfem_param, hfem_val, r) * (r - hfem_val.node_r_ele[e, 1]) / hfem_val.length[e],
                                                 hfem_val.node_r_ele[e, 1],
                                                 hfem_val.node_r_ele[e, 2],
                                                 vh_val)
                
                    _ => 0.0
                end
        end
    end
end

function make_element_matrix_and_vector_first(hfem_param, hfem_val, vh_val)
    # 要素行列とLocal節点ベクトルの各成分を計算
    for e = 1:hfem_param.ELE_TOTAL
        for i = 1:2
            for j = 1:2
                vh_val.mat_A_ele[e, i, j] = (-1) ^ i * (-1) ^ j / hfem_val.length[e]
            end

            vh_val.vec_b_ele[e, i] =
                @match i begin
                    1 => GaussLegendre.gl_integ(r -> 4.0 * r * exp(-2.0 * r) * (hfem_val.node_r_ele[e, 2] - r) / hfem_val.length[e],
                                                 hfem_val.node_r_ele[e, 1],
                                                 hfem_val.node_r_ele[e, 2],
                                                 vh_val)
                    
                    2 => GaussLegendre.gl_integ(r -> 4.0 * r * exp(-2.0 * r) * (r - hfem_val.node_r_ele[e, 1]) / hfem_val.length[e],
                                                 hfem_val.node_r_ele[e, 1],
                                                 hfem_val.node_r_ele[e, 2],
                                                 vh_val)
                
                    _ => 0.0
                end
        end
    end
end

function make_global_matrix_and_vector(hfem_param, hfem_val, vh_val)
    tmp_dv = zeros(hfem_param.NODE_TOTAL)
    tmp_ev = zeros(hfem_param.NODE_TOTAL - 1)

    vh_val.vec_b_glo = zeros(hfem_param.NODE_TOTAL)

    # 係数行列と右辺ベクトルを生成
    for e = 1:hfem_param.ELE_TOTAL
        for i = 1:2
            for j = 1:2
                if hfem_val.node_num_seg[e, i] == hfem_val.node_num_seg[e, j]
                    tmp_dv[hfem_val.node_num_seg[e, i]] += vh_val.mat_A_ele[e, i, j]
                elseif hfem_val.node_num_seg[e, i] + 1 == hfem_val.node_num_seg[e, j]
                    tmp_ev[hfem_val.node_num_seg[e, i]] += vh_val.mat_A_ele[e, i, j]
                end
            end
            
            vh_val.vec_b_glo[hfem_val.node_num_seg[e, i]] += vh_val.vec_b_ele[e, i]
        end
    end

    return tmp_dv, tmp_ev
end

自己無撞着問題の解法

上述のように，$ (13) $式および$ (15) $式は非線形連立常微分方程式になっており，SCF計算によって解を求めなければなりません．SCF計算の手続きは以下のようになります．

  1. 電子密度の初期値を適当に選びます．何でもいいのですが，著者は水素原子の厳密な電子密度$ 4\exp(-2r) $を電子密度の初期値$ n(r) $としました．
  2. この$ n(r) $から，$ (29) $式の連立方程式を解くことによって，$ U(r) $を計算します．
  3. 2.で求めた$ U(r)$を用いて，$ (20) $式の一般化固有値問題を数値的に解きます．
  4. 波動関数$ \phi(r) $を規格化（正規化）します．
  5. エネルギー
E=2E^{^{\prime}}-%
%TCIMACRO{\dint \nolimits_{0}^{r_{c}}}%
%BeginExpansion
{\displaystyle\int\nolimits_{0}^{r_{c}}}
%EndExpansion
rU\left(  r\right)  \left\vert \phi\left(  r\right)  \right\vert ^{2}dr \tag{29}

を求めます（この計算はこちらの記事や，こちらを参照してください．ここで，$ (29) $式は数値積分により求めなければなりません．
6. ステップ4で求まった波動関数$ \phi(r) $を二乗し，電子密度$ n(r) $を求めます．
7. ステップ2～6を繰り返します．

ここで，このままでは無限ループになってしまうので，どこかで計算を打ち切らなくてはなりません．通常は，前回計算したエネルギー$ E_{old} $と，今回計算したエネルギー$ E_{new} $の差の絶対値$ \left\vert E_{new}-E_{old}\right\vert $が，ある閾値未満になったところで計算を打ち切ります．

SCF計算でヘリウム原子のエネルギーを求めるJuliaのプログラム

SCF計算でヘリウム原子のエネルギーを求めるJuliaのプログラムは以下のようになります．ただし，全部載せると非常に長くなってしまうので，一部だけを掲載しています．なお，完全なコードはGitHubのこちらで公開しています．また，以上の全てのコードは，GitHubのこちらで公開しています．

function scfloop()
    # Schrödinger方程式を解くルーチンの初期処理
    hfem_param, hfem_val = Helium_HF_FEM_Eigen.construct()
    
    # 有限要素法のデータのみ生成
    Helium_HF_FEM_Eigen.make_wavefunction(0, hfem_param, hfem_val, nothing)
    
    # Poisson方程式を解くルーチンの初期処理
    vh_param, vh_val = Helium_Vh_FEM.construct(hfem_param)
    
    # 仮の電子密度でPoisson方程式を解く
    Helium_Vh_FEM.solvepoisson!(0, hfem_param, hfem_val, vh_val)

    # 新しく計算されたエネルギー
    enew = 0.0

    for iter in 1:MAXITER
        eigenenergy = Helium_HF_FEM_Eigen.make_wavefunction(iter, hfem_param, hfem_val, vh_val)
        
        # 前回のSCF計算のエネルギーを保管
        eold = enew
        
        # 今回のSCF計算のエネルギーを計算する
        enew = Helium_HF_FEM_Eigen.get_totalenergy(eigenenergy, hfem_param, hfem_val, vh_val)
        
        @printf "Iteration # %2d: HF eigenvalue = %.14f, energy = %.14f\n" iter eigenenergy enew
        
        # SCF計算が収束したかどうか
        if abs(enew - eold) <= THRESHOLD
            # 波動関数を規格化
            hfem_val.phi ./= sqrt(4.0 * pi)

            # 収束したのでhfem_param, hfem_val, エネルギーを返す
            return hfem_param, hfem_val, enew
        end
        
        # Poisson方程式を解く
        Helium_Vh_FEM.solvepoisson!(scfloop, hfem_param, hfem_val, vh_val)
    end

    return nothing
end

なお，これらのプログラムは，@Sunset_Yuhi様のこちらの記事の，fem1d_poisson01.pyを参考にさせて頂きました．

プログラムの実行結果

前節で紹介したプログラムを実行した結果は，以下の画像のようになります．
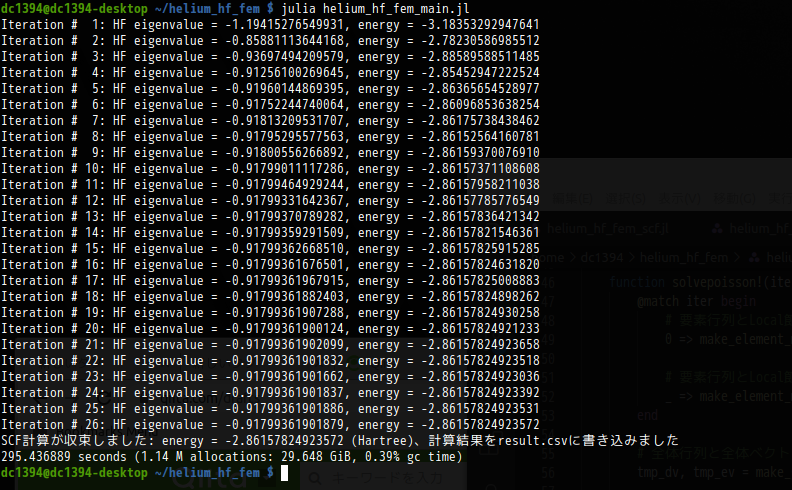
プログラム実行結果.png

$ N = 5000 $で，カットオフ$ r_c = 50.0(a.u.) $の場合，$ \left\vert E_{new}-E_{old}\right\vert $が，閾値（今の場合$ 5 \times 10^{-13} $）未満になるまでに，26回のループを要していることが分かります．

有限要素法を用いたヘリウム原子の基底状態のHartree-Fockエネルギーの計算結果の結果

ここで，この有限要素法のプログラムによる$ N = 100 $，$ N = 500 $，$ N = 1000 $，$ N = 5000 $のときの基底状態のHartree-Fockエネルギーの計算結果（ただし，$ r_{c} = 50.0(a.u.) $）を表に示しますと，以下のようになります（単位は全てHartree原子単位です）．

N 基底状態のエネルギー
100 -2.758369
500 -2.852320
1000 -2.859188
5000 -2.861578
Hartree-Fock極限 -2.861680

表から分かるとおり，$ N $が大きくなるほどHartree-Fock極限に近づいていることが分かります． 特に，$ N = 5000 $の時は，厳密な値の99.9964％のエネルギーを与え，非常に良好な結果となっています．

有限要素法を用いたヘリウム原子の基底状態のHartree-Fock波動関数と6個のGTOで展開したHartree-Fock波動関数との比較

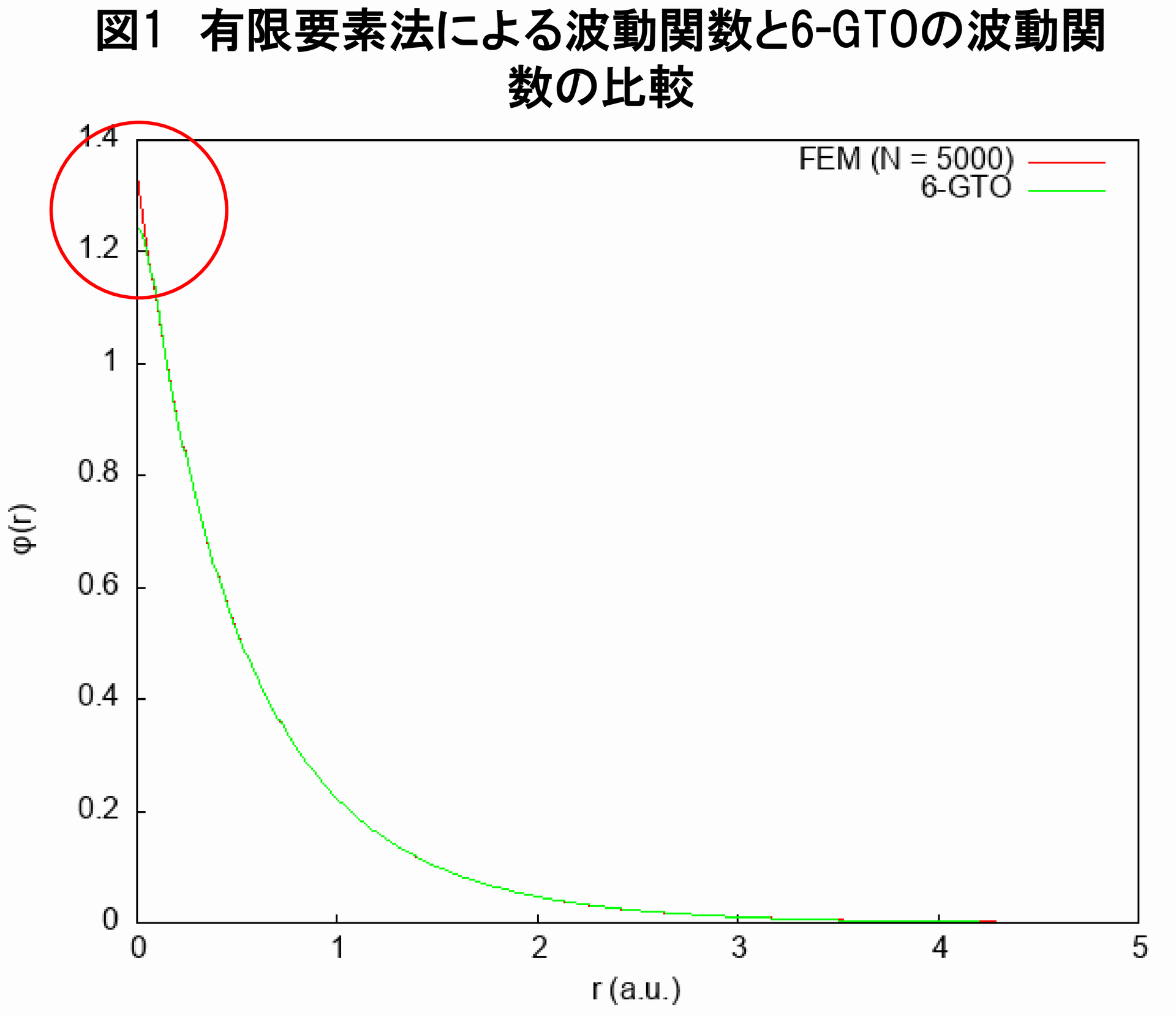
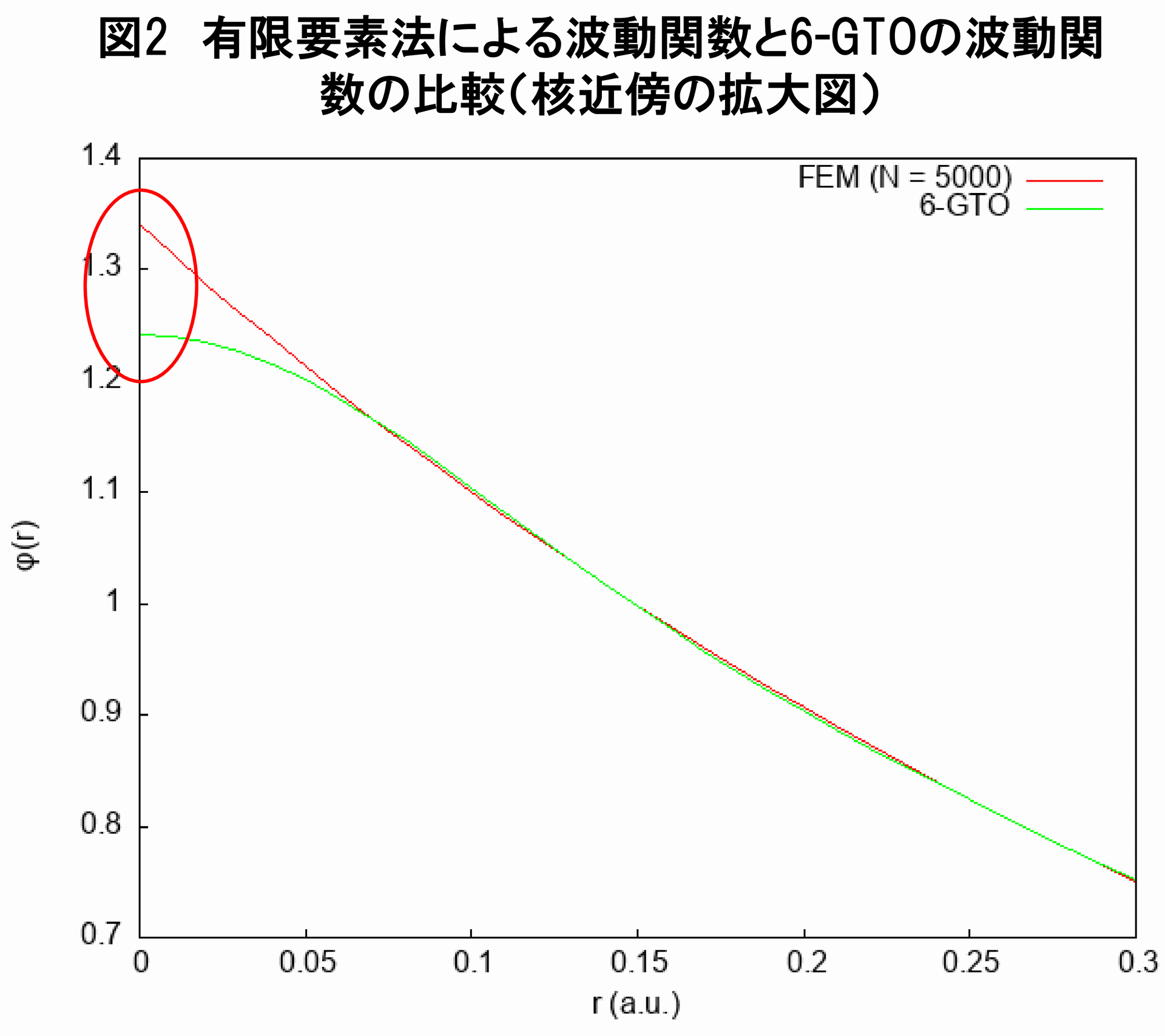
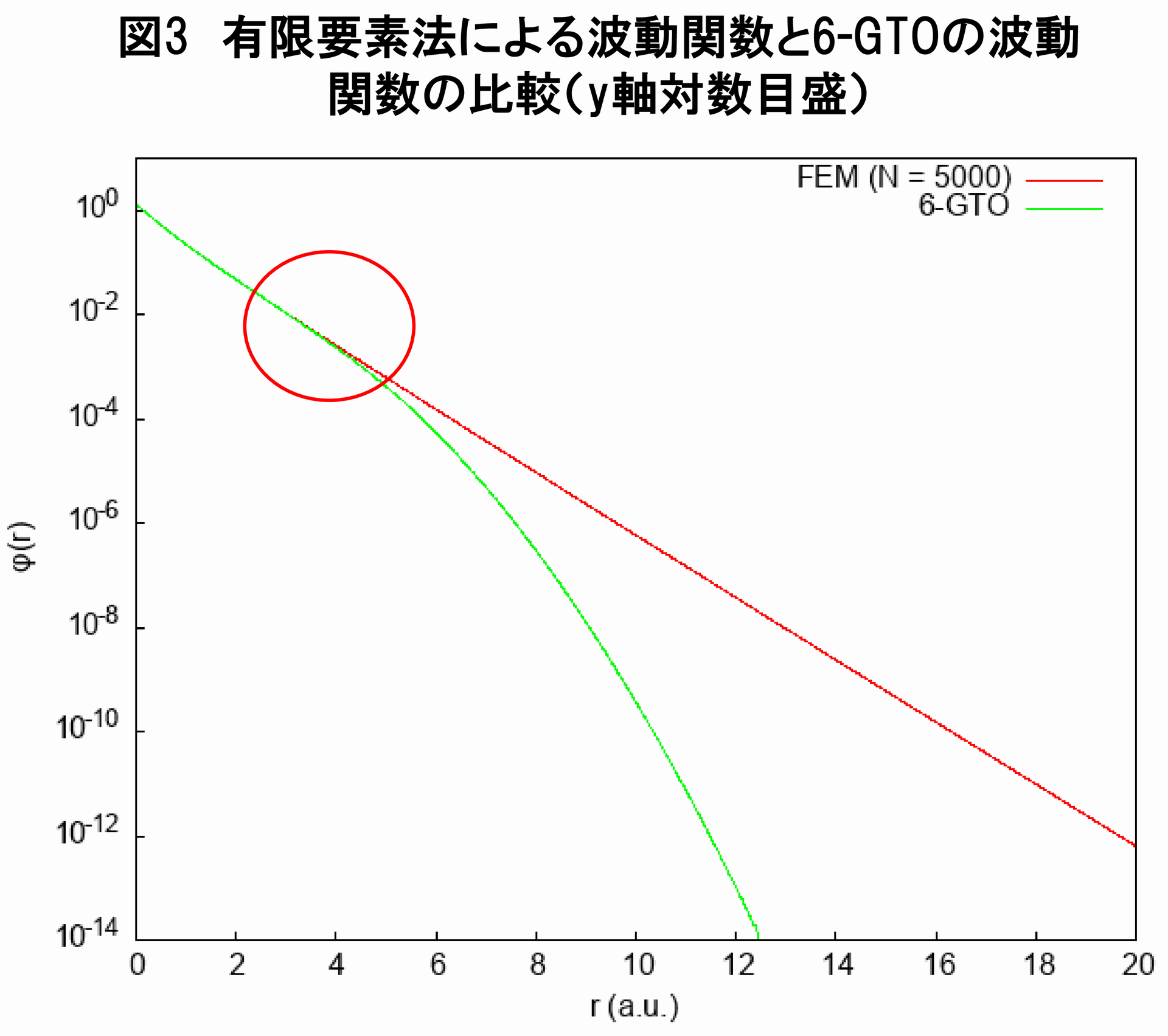
続いて，有限要素法を用いたヘリウム原子の基底状態のHartree-Fock波動関数（$ N = 5000 $，$ r_{c} = 50.0(a.u.) $のとき）と6個のGTOで展開したHartree-Fock波動関数とを，プロットで比較してみることにしましょう．

有限要素法と6-GTOの比較-01.png
有限要素法と6-GTOの比較-02.png
有限要素法と6-GTOの比較-03.png

図1と図2を見る限り，GTOで展開した場合と異なり，有限要素法によるHartree-Fock波動関数は原点でカスプを持ち，原点付近で指数関数の振る舞いをしています．また図3を見ると，これもGTOで展開した場合と異なり，遠方で指数関数で減衰していることが分かります（波動関数をGTOで展開したときに生じる問題については，こちらの記事をご覧ください）．

まとめ

  1. ヘリウム原子の基底状態のHartree-Fock方程式を弱形式にする方法を説明しました．
  2. Hartree-Fock方程式について，弱形式からローカル行列を生成し，ローカル行列の行列方程式から全体行列の行列方程式を求める方法について説明しました．
  3. Hartree-Fock方程式について，全体行列の行列方程式が，一般化固有値問題に帰着することを説明しました．
  4. Hartree-Fock方程式について，全体行列の境界条件処理について説明しました．
  5. 工程2.～4.と一般化固有値問題を解き，その解である波動関数を正規化するJuliaプログラムを紹介しました．
  6. ヘリウム原子のPoisson方程式を弱形式にする方法を説明しました．
  7. Poisson方程式について，弱形式から要素行列とローカル節点ベクトル（各要素における未知係数ベクトル）を生成し，要素行列から係数行列，ローカル節点ベクトルから右辺ベクトルを生成する方法について説明しました．
  8. Poisson方程式について，係数行列と右辺ベクトルが連立方程式を満たすことを説明しました．
  9. Poisson方程式について，係数行列と右辺ベクトルの境界条件処理について説明しました．
  10. 工程6.～9.と連立方程式を解くJuliaプログラムを紹介しました．
  11. 工程1.～11.はSCF（自己無撞着）計算を行わなければならないことを説明し，SCF計算を行うJuliaプログラムを紹介しました．
  12. 有限要素法によるヘリウム原子の基底状態のエネルギー固有値とHartree-Fock極限の比較を行いました
  13. 有限要素法によるヘリウム原子の基底状態の波動関数と，6個のGTOで展開した場合の波動関数との比較を行いました．

参考サイト

[1] Pythonで有限要素法（1次元Poisson方程式）

参考文献

J.M.ティッセン『計算物理学』シュプリンガー・フェアラーク東京（2003）

  1. 日本計算工学会編『計算力学（第2版）』森北出版（2012） ↩

  2. 菊地文雄『有限要素法概説―理工学における基礎と応用』サイエンス社（1999） ↩

8
9
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
8
9

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?