Pythonで数値計算プログラムを書き直そうシリーズもよければどうぞ。
2次元Helmholtz方程式を有限要素法で解くPythonプログラムを、GitHubに上げてみました。読みにくいコードかもしれませんが、固有値や固有ベクトルを愛でてみたい方、よければ使ってください。https://t.co/oPi2dlYGE8 pic.twitter.com/sm4RS0C1AG
— サンセット (@Sunset_Yuhi) 2019年5月28日
Qiita全体で数値計算の話題が少なそうだったので、有限要素法(finite element method, FEM)の記事を書いてみました。書き足りなかったり内容が曖昧な所があります。修正リクエストなど書いていただける方、お待ちしています。
1.解きたい問題
\frac{d}{dx} \left[ p(x) \frac{d u(x)}{dx} \right] = f(x)~~~ (a < x < b) \tag{1-1}
式(1-1)はPoisson(ポアソン)方程式と呼ばれる微分方程式で、非常に様々な分野で登場します。例えば、熱伝導や物質拡散、静電場(静磁場)や重力場、引張圧縮応力、非圧縮性流れなどを考える時に出てきます。$x$は位置座標、$p(x),f(x)$は既知の関数とし、未知関数である$u(x)$を求めるのが今回の目標です。しかし、微分方程式だけでは解が一意に定まらないため、現実的な計算では何か境界条件を決める必要があります。今回は境界条件を次のように置きます。
u(a) = \alpha,~~~ \frac{du(b)}{dx} = \beta \tag{1-2}
式(1-2)の第1式は定義域の左端で$u(x)$の値を直接決めるDirichlet(ディリクレ)境界条件、式(1-2)の第2式は定義域の右端で$u(x)$の傾きを決めるNeumann(ノイマン)境界条件です。
このように、微分方程式と境界条件からなる問題は、「境界値問題」と呼ばれます。
2.厳密解を求める
$p(x)$と$f(x)$が定数の時、この境界値問題の厳密解は、高校数学レベルの計算ですぐに求められます。まず式(1-1)について、$p$と$f$を1つの定数$f$にまとめて書き直すと、
$$\frac{d^2 u(x)}{dx^2} = f~~~ (a < x < b)$$
両辺を$x$で2回積分すると、
$$\frac{du(x)}{dx} = fx +C_1,~~~ u(x) = \frac{f}{2}x^2 +C_1 x +C_2$$
境界条件(1-2)を代入すると、
$$C_1 = -fb +\beta,~~~ C_2 = -\frac{f}{2}a^2 -(-fb +\beta)a +\alpha$$
よって、
$$u(x) = \frac{f}{2}x^2 +(-fb +\beta)x -\frac{f}{2}a^2 -(-fb +\beta)a +\alpha$$
この解はあとで、有限要素解析プログラムを検証するのに使います。
3.近似解の求め方を考える
微分方程式における関数$u(x)$の近似解を求める場合、非線形の関数で近似したり、Fourier(フーリエ)級数展開や差分法から計算する方法が考えられます。しかし、この精度には限界があります。例えば、Fourier級数展開ならGibbs(ギブズ)現象、差分法ならTaylor(テイラー)展開の打ち切り誤差などが、計算結果に無視できない誤差を与えます。
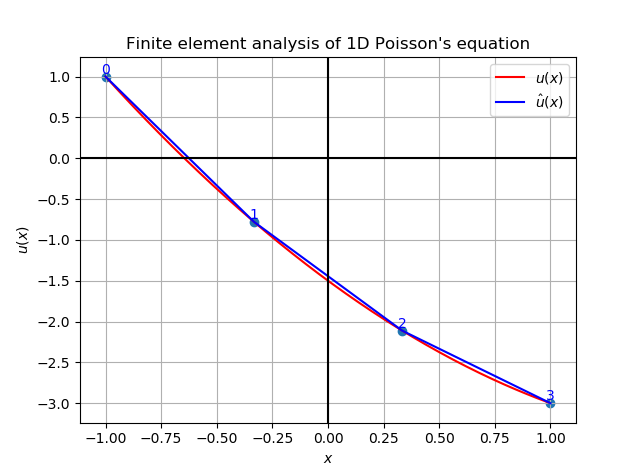
それでは、定義域を細かく分割して、分割した領域ごとに関数$u(x)$を近似するのはどうでしょうか。変化が激しい所ほど細かく分割すれば、区分線形関数でも精度よく近似できそうです。ここで一度、有限要素解析の結果を天下り的に見てしまいましょう。
赤線が厳密解、青線が有限要素法で求めた数値解ですが、厳密解にそって区分線形近似されていることが分かります。有限要素法では、まず定義域を多数の「要素」と呼ばれる領域に分割し、各要素の頂点には計算点である「節点」を定義します。定義域を有限個の要素に分割するので、「有限要素法」です。また、有限要素法で直接求めるのは節点上の$u(x)$の値で、それ以外の領域は線形関数などで補間して、解を得たとみなします。
ちなみに、有限個の節点上の$u(x)$は、元の境界値問題を線形連立方程式に置きかえてしまうことで計算します。そしてその定式化には、「重み付き残差法」の一種である「Galerkin(ガラーキン)法」というのを使います。専門用語が出てきましたが、考え方の基本としては上のグラフのように、小さな領域ごとに近似関数を求める方法と考えれば、いい取っ掛かりになるのではと思います。
4.近似関数の表現を考える
[TODO:local節点の値とglobal節点の値の対応を説明する。]
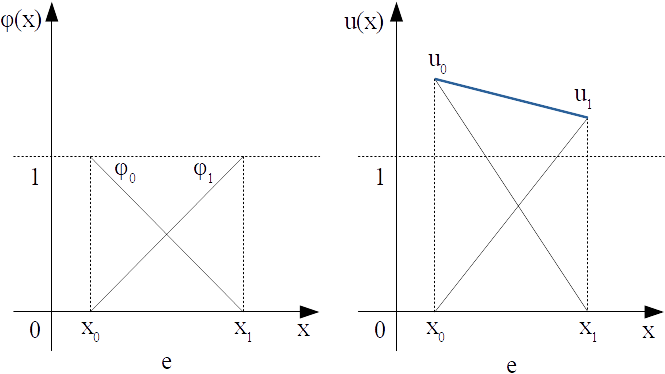
近似関数を要素ごとに求めるのが有限要素法の発想、ということは先に書きました。では、各要素における近似関数は、どう表現したらいいのでしょうか。区分線形近似をする場合、要素ごとに線形関数で近似することになりますが、この線形関数は要素の情報と結び付けて表す必要があります。そしてそれを実現するのが、形状関数というものです。今回は、左から$e$番目($e=0,1,\dots,N-1$)の要素における形状関数$\boldsymbol{\phi}^e(x)$を線形関数で定義します。2点$(x^e_0,1),(x^e_1,0)$を通る線形関数を$\phi_0^e(x)$、2点$(x^e_0,0),(x^e_1,1)$を通る線形関数を$\phi_1^e(x)$とすると、それぞれ次のように書けます。
\phi_0^e(x) = -\frac{x-x_1^e}{l^e},~~~~~ \phi_1^e(x) = \frac{x-x_0^e}{l^e}
ただし、$x^e_0,x^e_1$は$e$番目の要素をなす2節点の$x$座標、$l^e=x_1^e -x_0^e$は線分要素の長さです。ちなみに、番号を0から始めているのは、Pythonの配列番号が0から始まっているのに合わせたためです。また、この形状関数をグラフで表すと、左図のようになります。
この形状関数の特徴を考えてみましょう。まず線分要素の場合、1要素につき2節点あるので、形状関数も1要素につき2つ定義されることになります。また、この形状関数は、定義された節点上で1、それ以外の節点上では0となる関数になっています。そして最後に重要な点として、$\phi_0^e(x)$と$\phi_1^e(x)$を足し合わせると、高さが1の定数関数の線分になります(重ね合わせの原理)。
ここで、節点における近似関数の値$u_0^e$と$u_1^e$が分かったとします。$\phi_0^e(x)$を$u_0^e$倍、$\phi_1^e(x)$を$u_1^e$倍して、近似関数を$\hat{u}(x)$と書きます。この時、近似関数$\hat{u}(x)$は次のように表現できます。
\begin{align}
\hat{u}^e(x) = \boldsymbol{u}^e \cdot \boldsymbol{\phi}^e(x)~~~~~ (x_0^e \leq x \leq x_1^e)
\end{align}
ここで、$\boldsymbol{u}^e$は各要素における未知係数ベクトル、$\boldsymbol{\phi}^e(x)$は各要素における形状関数ベクトルと言います。この近似解をグラフで表すと、右図のようになります。この考え方で、各要素の形状関数$\boldsymbol{\phi}^e(x)$を何倍したら近似解になるかを求めます。これを要素ごとに行えば、先に見た有限要素解析の結果になる訳です。
5.支配方程式の弱形式化
[TODO:Galerkin法を紹介してから領域分割をするやり方に書き換える。]
では、重み付き残差法のプロセスに沿って、具体的に定式化しましょう。まず支配方程式(1-1)から残差$R(x)$というものを定義します。
R(x) = \frac{d}{dx} \left[ p(x) \frac{d u(x)}{dx} \right] -f(x) = 0 \tag{5-1}
この時、$u(x)$が真の解であれば$R(x)=0$となりますが、近似解$\hat{u}(x)$であれば$R(x) \simeq 0$となるはずです。そして次に、任意の重み関数$w(x)$を考え、$R(x)$に掛けて定義域内で積分します。$R(x) \to 0$となれば、この積分も0に収束すると期待できるので、次のように書けます(ただし、後の計算の便宜上、Dirichlet境界上では$w(x)=0$とします)。
\int_a^b R(x) w(x) dx = 0 \tag{5-2}
式(5-2)より、残差に重みを掛けて積分した時、それが0に収束するような$\hat{u}(x)$を求めれば、精度のよい近似解を求めたことになります。また、元の支配方程式(1-1)が一度積分されたことで、$u(x)$の微分可能回数の条件が1階だけ弱められています。このことから、式(5-2)は弱形式とも呼ばれます。重み付き残差法の一種であるGalerkin法は、この弱形式(5-2)を精度よく解くことができます。
重み付き残差法の中でもGalerkin法がよく使われる理由を知るには、変分法の一種であるRitz(リッツ)法との関係を理解する必要があります。Ritz法を含む変分法は、弱形式の解を求められることが数学的に保証されています。そのため、本来なら弱形式を解くには変分法を使いたいのですが、計算が煩雑になるという欠点があります。一方、Galerkin法で定式化した式は、Ritz法で定式化した式と全く同じ式になるという特徴があります。ただし、元の関数$u(x)$の汎関数が存在する場合に限ります。汎関数は、関数を変数に持つ関数、言わば関数の関数です。
そして、Galerkin法の方がRitz法よりも計算方法が単純なので、Galerkin法で定式化することが多いのです。なお、2つの名前を折衷して「Ritz-Galerkin法」と呼ぶこともあります。
さて、弱形式(5-2)をもう少し整理しましょう。まず、弱形式(5-2)の左辺を展開してみます。
\int_a^b R(x) w(x) dx = \int_a^b \frac{d}{dx} \left[ p(x) \frac{d u(x)}{dx} \right] w(x) dx -\int_a^b f(x) w(x) dx \tag{5-3}
ここで1つテクニックを使い、更に式を展開します。Gauss(ガウス)の発散定理を使う方法もありますが、今回は式(5-3)の右辺第1項に対して、部分積分の式を適用してみましょう。それを式(5-2)に戻すと、次のように書けます。
\left[ p(x) \frac{d u(x)}{dx} w(x) \right]^b_a -\int_a^b p(x) \frac{d u(x)}{dx} \frac{dw(x)}{dx} dx -\int_a^b f(x) w(x) dx = 0 \tag{5-4}
ここで現れた左辺第1項が重要です。境界条件はこの項を利用して入れてやります。ただし、Dirichlet境界上では$w(x)=0$、Neumann境界上では$\frac{du(b)}{dx} = \beta$なので、定積分項では$p(a) \frac{du(a)}{dx} w(a) = 0$、$p(b) \frac{du(b)}{dx} w(b) = p(b) \beta w(b)$となり、式(5-4)は次のように単純化できます。
p(b) \beta w(b) -\int_a^b p(x) \frac{du(x)}{dx} \frac{dw(x)}{dx} dx -\int_a^b f(x) w(x) dx = 0 \tag{5-5}
まとめとして、式(5-2)~(5-5)までの式展開を続けて書いてみます。自分が定式化をする時には、このように一度に書くことが多いです。
\begin{align}
\int_a^b R(x) w(x) dx &= \int_a^b \left\{ \frac{d}{dx} \left[ p(x) \frac{d u(x)}{dx} \right] -f(x) \right\} w(x) dx~~~~~ (残差を代入した)
\\
&= \int_a^b \frac{d}{dx} \left[ p(x) \frac{d u(x)}{dx} \right] w(x) dx -\int_a^b f(x) w(x) dx~~~~~ (展開した)
\\
&= \left[ p(x) \frac{d u(x)}{dx} w(x) \right]^b_a -\int_a^b p(x) \frac{d u(x)}{dx} \frac{dw(x)}{dx} dx -\int_a^b f(x) w(x) dx~~~~~ (部分積分した)
\\
&= p(b) \beta w(b) -\int_a^b p(x) \frac{du(x)}{dx} \frac{dw(x)}{dx} dx -\int_a^b f(x) w(x) dx~~~~~ (境界条件を入れた)
\\
&= 0~~~~~ (R(x) \to 0なら弱形式も0)
\end{align}
6.弱形式の離散化
[TODO:ちゃんと導出する。]
式(4-5)の左辺第2項と第3項を、$N$個の領域(要素)に離散化しましょう。式(4-5)の左辺第1項は、要素ごとというよりも全体の領域の境界に対する条件なので、一旦後回しで考えます。
\begin{align}
\int_a^b p(x) \frac{du(x)}{dx} \frac{dw(x)}{dx} dx &= \sum_{e=0}^{N-1} \int_{x_0^e}^{x_1^e} p^e(x) \frac{du^e(x)}{dx} \frac{dw^e(x)}{dx} dx \tag{6-1}
\\
\int_a^b f(x) w(x) dx &= \sum_{e=0}^{N-1} \int_{x_0^e}^{x_1^e} f^e(x) w^e(x) dx \tag{6-2}
\end{align}
続いて、$e$番目の要素内の未知関数$u(x)$および重み関数$w(x)$を、形状関数を用いてさらに離散化します。重み関数は本来任意の関数でよいのですが、形状関数と同じ関数にすると計算精度が上がることが知られており、その方法こそがGalerkin法と呼ばれています。今回はGalerkin法に従って、重み関数は形状関数と同じ形にします。
\begin{align}
u^e(x) = \sum_{i=0}^1 u_i^e \phi_i^e(x) \tag{6-3}
\\
w^e(x) = \sum_{i=0}^1 w_i^e \phi_i^e(x) \tag{6-4}
\end{align}
すると式(6-1)、(6-2)は、次のように離散化されます。
\sum_{e=0}^{N-1} \int_{x_0^e}^{x_1^e} p_i^e \frac{d u_i^e \phi_i^e(x)}{dx} \frac{d \phi_j^e(x)}{dx} dx = \sum_{e=0}^{N-1} \sum_{i=0}^1 p_i^e \frac{ (-1)^{i+1} (-1)^{j+1} }{l^e} u_i^e~~~~~ (j=0,1) \tag{6-5}
\sum_{e=0}^{N-1} \int_{x_0^e}^{x_1^e} f^e \phi_i^e(x) dx = \sum_{e=0}^{N-1} \sum_{i=0}^1 f^e \frac{l^e}{2} \tag{6-6}
7.要素ごとに連立方程式を作る
この辺はプログラムを見たほうが早いかもしれません。
離散化した式を元に、各要素で成り立つ連立方程式を作ります。これを要素方程式といいます。行列$\boldsymbol{A}^e$の次数は2です(要素の節点数と同じ)。
\begin{bmatrix}
A^e_{0,0}& A^e_{0,1}\\
A^e_{1,0}& A^e_{1,1}
\end{bmatrix}
\begin{Bmatrix}
u^e_0\\ u^e_1
\end{Bmatrix}
= \begin{Bmatrix}
b^e_0\\ b^e_1
\end{Bmatrix}
$$\boldsymbol{A}^e \boldsymbol{u}^e = \boldsymbol{b}^e$$
$$A_{ij}^e = \sum_{e=0}^{N-1} \sum_{i=0}^1 p_i^e \frac{ (-1)^{i+1} (-1)^{j+1} }{l^e} u_i^e~~~ (j=0,1),~~~~~ b_i = -\sum_{e=0}^{N-1} \sum_{i=0}^1 f^e \frac{l^e}{2}$$
8.領域全体で成り立つ連立方程式を作る
次に、要素方程式の行列成分を、全体で成り立つように組み立てなおします。これを全体方程式といいます。行列$\boldsymbol{A}^e$の次数はNです(全体の節点数と同じ)。
\begin{bmatrix}
A_{0,0}& \cdots& A_{0,N-1}\\
\vdots& \ddots& \vdots\\
A_{N-1,0}& \cdots& A_{N-1,N-1}
\end{bmatrix}
\begin{Bmatrix}
u_0\\ \vdots\\ u_{N-1}
\end{Bmatrix}
= \begin{Bmatrix}
b_0\\ \vdots\\ b_{N-1}
\end{Bmatrix}
$$\boldsymbol{A} \boldsymbol{u} = \boldsymbol{b}$$
要素方程式の各成分を、全体方程式の各成分にどう足しこむかが問題になりますが、要素の節点に対応する全体の節点に対して、節点上の値をひも付ければいいです。また、有限要素法で扱う行列は巨大になることも多いため、本来は行列の圧縮形式などを工夫する必要がありますが、今回は説明の簡略化のために省略します。
9.境界条件処理
[TODO:定式化からこの処理の正当性を確かめる。]
この辺もプログラムを見た方が早いかもしれません。
Dirichlet境界条件の処理をする場合は、まず$[\boldsymbol{A}]$のn行目に$\alpha$をかけたものを${\boldsymbol{u}}$から引き、${\boldsymbol{u}}$のn行目を$\alpha$にします。そして、$[\boldsymbol{A}]$の(n,n)成分を1、それ以外のn行とn列成分を0にすれば完了です。
Neumann境界条件を実装する場合は,定義域の端に当たる節点に処理します。${\boldsymbol{u}}$の$n$行目に$\beta$を加えれば完了です。
10.プログラム
[TODO:処理を関数で分けて、モジュールとして使える書き方にする。]
#1次元Poisson方程式を、有限要素法で解く
#d/dx[p(x)du(x)/dx]=f(x) (x_min<x<x_max)
#u(x_min)=alpha, du(x_max)/dx=beta
import time #時刻を扱うライブラリ
import numpy as np #NumPyライブラリ
import scipy.linalg #SciPyの線形計算ライブラリ
import matplotlib.pyplot as plt #データ可視化ライブラリ
x_min = -1.0 #計算領域のXの最小値
x_max = 1.0 #計算領域のXの最大値
node_total = 4 #節点数(>=2)
ele_total = node_total-1 #要素数
func_f = 1.0 #定数関数f
#境界条件u(x_min)=alpha,du(x_max)/dx=beta。
#alphaやbetaが"inf"の時は、何も処理しないようにする。
alpha = 1.0 #左端のディリクレ境界条件
beta = -1.0 #右端のノイマン境界条件
#任意の節点に境界条件を実装する
def boundary(node_num_glo, Dirichlet, Neumann):
#ディリクレ境界条件
if (Dirichlet!="inf"): #Dirichlet=無限大の時は処理しない
vec_b_glo[:] -= Dirichlet*mat_A_glo[node_num_glo,:] #定数ベクトルに行の値を移項
vec_b_glo[node_num_glo] = Dirichlet #関数を任意の値で固定
mat_A_glo[node_num_glo,:] = 0.0 #行を全て0にする
mat_A_glo[:,node_num_glo] = 0.0 #列を全て0にする
mat_A_glo[node_num_glo,node_num_glo] = 1.0 #対角成分は1にする
#ノイマン境界条件
if (Neumann!="inf"): #Neumann=無限大の時は処理しない
vec_b_glo[node_num_glo] += Neumann #関数を任意の傾きで固定
############### 入力データの用意 ###############
#計算の開始時刻を記録
compute_time = time.time()
print("node_total = ",node_total, ", ele_total = ",ele_total)
#Global節点のx座標を定義(x_min〜x_max)
print("Global node X")
node_x_glo = np.empty(node_total, np.float64) #Global節点のx座標
node_x_glo = np.linspace(x_min,x_max, node_total) #計算領域を等分割
print(node_x_glo)
#各要素のGlobal節点番号
print("Node number of each elements")
node_num_glo_in_seg_ele = np.empty((ele_total,2), np.int) #各要素のGlobal節点番号
for e in range(ele_total):
node_num_glo_in_seg_ele[e,0] = e
node_num_glo_in_seg_ele[e,1] = e+1
print(node_num_glo_in_seg_ele)
#各要素のLocal節点座標
print("Local node X")
node_x_ele = np.empty((ele_total,2), np.float64) #各要素のLocal節点のx座標
for e in range(ele_total):
for i in range(2):
node_x_ele[e,i] = node_x_glo[ node_num_glo_in_seg_ele[e,i] ]
print(node_x_ele)
########## 要素行列を求める ##########
#各線分要素の長さを計算
print("Element length")
length = np.empty(ele_total, np.float64) #各要素の長さ
for e in range(ele_total):
length[e] = np.absolute( node_x_ele[e,1] -node_x_ele[e,0] )
print(length)
#要素行列の初期化
mat_A_ele = np.zeros((ele_total,3,3), np.float64) #要素係数行列(ゼロで初期化)
vec_b_ele = np.zeros((ele_total,3), np.float64) #要素係数ベクトル(ゼロで初期化)
#要素行列の各成分を計算
print("Local matrix")
for e in range(ele_total):
for i in range(2):
for j in range(2):
mat_A_ele[e,i,j] = ( (-1)**(i+1) *(-1)**(j+1) ) / length[e]
vec_b_ele[e,i] = -func_f *length[e]/2.0
########## 全体行列を組み立てる ##########
#全体行列の初期化
mat_A_glo = np.zeros((node_total,node_total), np.float64) #全体係数行列(ゼロで初期化)
vec_b_glo = np.zeros(node_total, np.float64) #全体係数ベクトル(ゼロで初期化)
#要素行列から全体行列を組み立てる
print("Global matrix (constructed)")
for e in range(ele_total):
for i in range(2):
for j in range(2):
mat_A_glo[ node_num_glo_in_seg_ele[e,i], node_num_glo_in_seg_ele[e,j] ] += mat_A_ele[e,i,j]
vec_b_glo[ node_num_glo_in_seg_ele[e,i] ] += vec_b_ele[e,i]
if (node_total<20): #節点数が20未満の時、全体行列を確認
for i in range(node_total):
for j in range(node_total):
print("{:6.2f}".format(mat_A_glo[i,j]), end='')
print(";{:6.2f}".format(vec_b_glo[i]))
############### 境界条件処理 ###############
print("Boundary conditions")
boundary(0, alpha, 0.0) #左端はディリクレ境界
boundary(node_total-1, "inf", beta) #右端はノイマン境界
print("Post global matrix") #節点数が20未満の時、全体行列を確認
if (node_total<20):
for i in range(node_total):
for j in range(node_total):
print("{:6.2f}".format(mat_A_glo[i,j]), end='')
print(";{:6.2f}".format(vec_b_glo[i]))
############### 連立方程式を解く ###############
print('node_total = ',node_total, ', ele_total = ',ele_total)
#print('detA = ', scipy.linalg.det(mat_A_glo)) #Aの行列式
#print('Rank A = ', np.linalg.matrix_rank(mat_A_glo)) #AのRank(階数)
#print('Inverse A = ', scipy.linalg.inv(mat_A_glo)) #Aの逆行列
print('Unkown vector u = ') #未知数ベクトル
unknown_vec_u = scipy.linalg.solve(mat_A_glo,vec_b_glo) #Au=bから、未知数ベクトルuを求める
print(unknown_vec_u)
print('Max u = ', max(unknown_vec_u), ', Min u = ',min(unknown_vec_u)) #uの最大値、最小値
#計算時間の表示
compute_time = time.time() -compute_time
print ('compute_time: {:0.5f}[sec]'.format(compute_time))
############### 計算結果を可視化 ###############
#plt.rcParams['font.family'] = 'Times New Roman' #全体のフォントを設定
#plt.rcParams['font.size'] = 10 #フォントサイズを設定
#plt.rcParams['lines.linewidth'] = 2 # 線の太さ設定
#plt.title("Finite element analysis of 1D Poisson's equation") #グラフタイトル
plt.xlabel("$x$") #x軸の名前
plt.ylabel("$u(x)$") #y軸の名前
plt.grid() #点線の目盛りを表示
#厳密解をプロット
exact_x = np.arange(x_min,x_max,0.01)
exact_y = (func_f/2)*exact_x**2 +(-func_f*x_max +beta)*exact_x \
-(func_f/2)*x_min**2 -(-func_f*x_max +beta)*x_min +alpha
plt.plot(exact_x,exact_y, label="$u(x)$", color='#ff0000') #折線グラフを作成
#近似解をプロット
plt.plot(node_x_glo,unknown_vec_u, label="$\hat{u}(x)$", color='#0000ff') #折線グラフを作成
plt.scatter(node_x_glo,unknown_vec_u) #点グラフを作成
#更に体裁を整える
plt.axis('tight') #余白を狭くする
plt.axhline(0, color='#000000') #x軸(y=0)の線
plt.axvline(0, color='#000000') #y軸(x=0)の線
plt.legend(loc='best') #凡例(グラフラベル)を表示
for n in range(node_total): #節点番号をグラフ内に表示
plt.text(node_x_glo[n],unknown_vec_u[n], n, ha='center',va='bottom', color='#0000ff')
plt.show() #グラフを表示
#plt.savefig('fem1d_poisson.pdf')
#plt.savefig('fem1d_poisson.png')
11.資料とか
J. L. Volakis, A. Chatterjee, and L. C. Kempel, Finite Element Method for Electromagnetics, Wiley-IEEE Press, (1998).
竹内則雄, 樫山和男, 寺田賢二郎, 日本計算工学会編, 計算力学 第2版 有限要素法の基礎, 森北出版, (2012).
菊地文雄, 有限要素法概説 理工学における基礎と応用, コロナ社, (1999).
奥田洋司, 1次元問題の有限要素法, 東京大学大学院, (2006).
中島研吾, 有限要素法で学ぶ並列プログラミングの基礎, 東京大学, (2018).
中島研吾, 一日速習:三次元並列有限要素法とハイブリッド並列プログラミング, 東京大学, (2017).
畔上秀幸, シミュレーション工学特論, 名古屋大学, (2018).
日本建築学会編, はじめての音響数値シミュレーション プログラミングガイド, コロナ社, (2012).
JIKO, FEM基礎理論, CAE技術者のための情報サイト.
南木集, 1,2次元Poisson方程式に対する有限要素法, 明治大学理工学部, (2004).
Freeball, Bar Element - Coding in Python, Youtube, (2016).