水素原子に対するSchrödinger方程式を有限要素法で数値的に解いてみる（C++とJuliaのソースコード付き）

この記事では，水素原子に対するSchrödinger方程式を有限要素法（Finite Element Method，FEM）で，数値的に解いてみることにします．有限要素法自体については，この記事ではあまり深入りしません（有限要素法自体の解説は，@Sunset_Yuhi様のこちらの記事や、参考文献¹，参考文献²などが分かりやすいのではないかと思います）．

水素原子に対するSchrödinger方程式

さて，早速ですが，水素原子に対するSchrödinger方程式は，Hartree原子単位系で（以下，断りなしにHartree原子単位系を用いることとします），

\left(  -\dfrac{1}{2}\nabla^{2}-\dfrac{1}{r}\right)  \psi\left(
r\right)  =E\psi\left(  r\right) \tag{1}

となります．本来ならば，$ (1) $式を，3次元有限要素で離散化して数値的に解きたいところですが，正直に言って，3次元有限要素法は複雑なのであまりやりたくありません．従って，今回は，水素原子のs状態のエネルギー固有値と波動関数（固有関数）のみを求めることにします．水素原子のs状態の波動関数は球対称なので，ラプラシアンは，

\nabla^{2}=\dfrac{d^{2}}{dr^{2}}+\dfrac{2}{r}\dfrac{d}{dr} \tag{2}

となります（1次元なので，偏微分記号の代わりに常微分記号を用いました）．$ (2) $式を$ (1) $式に代入すると，

\left(  -\dfrac{1}{2}\dfrac{d^{2}}{dr^{2}}-\dfrac{1}{r}\dfrac{d}{dr}%
-\dfrac{1}{r}\right)  \psi\left(  r\right)  =E\psi\left(  r\right) \tag{3}

となります．これで$ (1) $式を1次元問題に帰着できましたので，$ (3) $式を1次元有限要素で離散化して数値的に解くことにします．

水素原子のs状態に対するSchrödinger方程式を弱形式にする

では早速，$ (3) $式の両辺に，左から重み関数$ \omega(r) $を乗じて，全空間で部分積分することにより，弱形式にしていきましょう．ここで，重み関数$ \omega(r) $には，波動関数$ \psi(r) $の複素共役である$ \psi^{\ast}(r) $を用います（もっとも，水素原子のs状態の波動関数は実関数なので，$ \psi(r) $と$ \psi^{\ast}(r) $は等しくなります）．ただし，ここで注意するべきことは，$ (3) $式括弧の中の第2項と第3項が原点で発散してしまうので，原点から積分できない点です．この問題は，$ r^{2} $を両辺に乗じてから部分積分することで解決できます．従って，部分積分するべき式は，

%
%TCIMACRO{\dint \nolimits_{0}^{\infty}}%
%BeginExpansion
{\displaystyle\int\nolimits_{0}^{\infty}}
%EndExpansion
r^{2}\psi^{\ast}\left(  r\right)  \left(  -\dfrac{1}{2}\dfrac{d^{2}}{dr^{2}%
}-\dfrac{1}{r}\dfrac{d}{dr}-\dfrac{1}{r}\right)  \psi\left(  r\right)  dr=E%
%TCIMACRO{\dint \nolimits_{0}^{\infty}}%
%BeginExpansion
{\displaystyle\int\nolimits_{0}^{\infty}}
%EndExpansion
r^{2}\psi^{\ast}\left(  r\right)  \psi\left(  r\right)  dr \tag{4}

となります．ただし，コンピュータでは無限大を扱えないので，実際には，適当なカットオフ$ r_{c} $を設けて，

%
%TCIMACRO{\dint \nolimits_{0}^{r_{c}}}%
%BeginExpansion
{\displaystyle\int\nolimits_{0}^{r_{c}}}
%EndExpansion
r^{2}\psi^{\ast}\left(  r\right)  \left(  -\dfrac{1}{2}\dfrac{d^{2}}{dr^{2}%
}-\dfrac{1}{r}\dfrac{d}{dr}-\dfrac{1}{r}\right)  \psi\left(  r\right)  dr=E%
%TCIMACRO{\dint \nolimits_{0}^{r_{c}}}%
%BeginExpansion
{\displaystyle\int\nolimits_{0}^{r_{c}}}
%EndExpansion
r^{2}\psi^{\ast}\left(  r\right)  \psi\left(  r\right)  dr \tag{5}

を，部分積分することになります．そして，

\psi\left(  r_{c}\right)  =\psi^{\ast}\left(  r_{c}\right)  =0 \tag{6}

を，境界条件として設定してやります．ここで，$ (5) $式を部分積分すると，

%
%TCIMACRO{\dint \nolimits_{0}^{r_{c}}}%
%BeginExpansion
{\displaystyle\int\nolimits_{0}^{r_{c}}}
%EndExpansion
\left[  \dfrac{r^{2}}{2}\dfrac{d\psi^{\ast}\left(  r\right)  }{dr}\dfrac
{d\psi\left(  r\right)  }{dr}-r\psi^{\ast}\left(  r\right)  \psi\left(
r\right)  \right]  dr=E%
%TCIMACRO{\dint \nolimits_{0}^{r_{c}}}%
%BeginExpansion
{\displaystyle\int\nolimits_{0}^{r_{c}}}
%EndExpansion
r^{2}\psi^{\ast}\left(  r\right)  \psi\left(  r\right)  dr \tag{7}

なる，弱形式が得られます（この計算は，こちらを参照してください）．

弱形式からローカル行列を生成する

では，$ (7) $式からローカル行列を生成していきましょう．$ (7) $式を$ N $個の要素で離散化することにより，

%
%TCIMACRO{\dsum \limits_{e=0}^{N-1}}%
%BeginExpansion
{\displaystyle\sum\limits_{e=0}^{N-1}}
%EndExpansion%
%TCIMACRO{\dint \nolimits_{r_{0}^{e}}^{r_{1}^{e}}}%
%BeginExpansion
{\displaystyle\int\nolimits_{r_{0}^{e}}^{r_{1}^{e}}}
%EndExpansion
\left[  \dfrac{r^{2}}{2}\dfrac{d\psi^{\ast}\left(  r\right)  }{dr}\dfrac
{d\psi\left(  r\right)  }{dr}-r\psi^{\ast}\left(  r\right)  \psi\left(
r\right)  \right]  dr=E%
%TCIMACRO{\dsum \limits_{e=0}^{N-1}}%
%BeginExpansion
{\displaystyle\sum\limits_{e=0}^{N-1}}
%EndExpansion%
%TCIMACRO{\dint \nolimits_{r_{0}^{e}}^{r_{1}^{e}}}%
%BeginExpansion
{\displaystyle\int\nolimits_{r_{0}^{e}}^{r_{1}^{e}}}
%EndExpansion
r^{2}\psi^{\ast}\left(  r\right)  \psi\left(  r\right)  dr \tag{8}

なる式が得られます．ここで，$ r_{0}^{e},r_{1}^{e} $は$ e $番目（$ e=0,1,\dots,N-1 $）の要素をなす2節点の$ r $座標です．さてここで，

r=el^{e}+yl^{e} \tag{9}

l^{e}=r_{1}^{e}-r_{0}^{e} \tag{10}

とおき，変数変換すると，

r_{0}^{e}=el^{e} \tag{11}

r_{1}^{e}=\left(  e+1\right)  l^{e} \tag{12}

となります．さらに，形状関数（重み関数）を，

\psi\left(  y\right)  =\psi^{\ast}\left(  y\right)  =%
%TCIMACRO{\dsum \limits_{i=0}^{1}}%
%BeginExpansion
{\displaystyle\sum\limits_{i=0}^{1}}
%EndExpansion
\psi_{i}^{e}\phi_{i}\left(  y\right)  ,\left(  0\leq y\leq1\right) \tag{13}

\phi_{0}\left(  y\right)  =1-y \tag{14}

\phi_{1}\left(  y\right)  =y \tag{15}

とします（ここで，$ \psi_{i}^{e} $は各要素における未知係数ベクトルの要素です），ここで，$ (9) $式～$ (15) $式を$ (8) $式に代入すると，左辺の$ 2 \times 2 $ローカル行列$ \mathbf{A} $と，右辺の$ 2 \times 2 $ローカル行列$ \mathbf{B} $が得られます．通常の微分方程式を有限要素で離散化すると，左辺がローカル行列と各要素における未知係数ベクトルの積で，右辺がベクトルの連立方程式が得られます．**しかし，Schrödinger方程式を有限要素で離散化すると，左辺と右辺にローカル行列が一つずつ現れ，行列方程式となります．**これは，Schrödinger方程式が固有方程式であり，エネルギー固有値$ E $も未知数であるためです．
さて，左辺のローカル行列$ \mathbf{A}^{(e)} $と，右辺のローカル行列$ \mathbf{B}^{(e)} $は，次の行列方程式を満たします（参考文献³）．

\left\langle \psi_{\alpha}^{\left(  e\right)  }\right\vert A_{\alpha\beta
}^{\left(  e\right)  }\left\vert \psi_{\beta}^{\left(  e\right)
}\right\rangle =\left\langle \psi_{\alpha}^{\left(  e\right)  }\right\vert
B_{\alpha\beta}^{\left(  e\right)  }\left\vert \psi_{\beta}^{\left(  e\right)
}\right\rangle \tag{16}

ここで，左辺のローカル行列$ \mathbf{A} $の成分$ A_{\alpha\beta}^{\left( e\right) } $は，

A_{00}^{\left(  e\right)  }=\dfrac{l^{e}}{2}\left(  e^{2}+e+\dfrac{1}
{3}\right)  -\left(  l^{e}\right)  ^{2}\left(  \dfrac{e}{3}+\dfrac{1}
{12}\right) \tag{17}

A_{01}^{\left(  e\right)  }=A_{10}^{\left(  e\right)  }=-\dfrac{l^{e}}
{2}\left(  e^{2}+e+\dfrac{1}{3}\right)  -\left(  l^{e}\right)  ^{2}\left(
\dfrac{e}{6}+\dfrac{1}{12}\right) \tag{18}

A_{11}^{\left(  e\right)  }=\dfrac{l^{e}}{2}\left(  e^{2}+e+\dfrac{1}
{3}\right)  -\left(  l^{e}\right)  ^{2}\left(  \dfrac{e}{3}+\dfrac{1}
{4}\right) \tag{19}

となります．また，右辺のローカル行列$ \mathbf{B} $の成分$ B_{\alpha\beta}^{\left( e\right) } $は，

B_{00}^{\left(  e\right)  }=\left(  l^{e}\right)  ^{3}\left(
\dfrac{e^{2}}{3}+\dfrac{e}{6}+\dfrac{1}{30}\right) \tag{20}

B_{01}^{\left(  e\right)  }=B_{10}^{\left(  e\right)  }=\left(  l^{e}\right)
^{3}\left(  \dfrac{e^{2}}{6}+\dfrac{e}{6}+\dfrac{1}{20}\right) \tag{21}

B_{11}^{\left(  e\right)  }=\left(  l^{e}\right)  ^{3}\left(  \dfrac{e^{2}%
}{3}+\dfrac{e}{2}+\dfrac{1}{5}\right) \tag{22}

となります（この計算は，こちらを参照してください）．

ローカル行列から全体行列を生成し，一般化固有値問題を導く

次に，ローカル行列から全体行列$ \mathbf{H} $と$ \mathbf{U} $が満たす行列方程式を生成します．これは，全体行列の対角要素（最初と最後を除く）が隣接する要素からの寄与の合計であることに注意して，要素ごとに$ (16) $式を重ね合わせることで可能です．これにより，以下の行列方程式が得られます．

\left\langle \psi_{i}\right\vert H_{ij}\left\vert \psi_{j}\right\rangle
=\left\langle \psi_{i}\right\vert U_{ij}\left\vert \psi_{j}\right\rangle
,\left(  i,j=0,\ldots,N-1\right) \tag{23}

ただし，$ H_{ij} $は，$ N $次正方行列$ \mathbf{H} $の成分，$ U_{ij} $は，$ N $次正方行列$ \mathbf{U} $の成分です．ここで，変分原理を用いると，$ (23) $式から結局，

H_{ij}\left\vert \psi_{j}\right\rangle =EU_{ij}\left\vert \psi_{j}%
\right\rangle \tag{24}

なる，一般化固有値問題が得られます．ここで，$ E $は，水素原子のs状態のエネルギー固有値です．

境界条件処理

~~なお，Schrödinger方程式を有限要素で離散化した場合，通常の有限要素法と異なり，境界条件の処理は不要です（そもそも，上述したように，$ E $が未知数であるため，境界条件の処理を行いたくてもできません）．~~などと書いていましたが、やはり境界条件処理は必要のようです（Twitterでご指摘を多数頂きました．ありがとうございます）．境界条件は，$ \psi(0) $ = 有限，$ \psi(r_{c}) $ = 0ですが，後者の境界条件処理は簡単で，全体行列$ \mathbf{H} $と$ \mathbf{U} $の，$ N $行目と$ N $列目を削るだけです．前者については，Twitterで@moshi_moshi_9様が，以下のようなツイートをされていましたので，結局，境界条件処理は不要のようです．@moshi_moshi_9様，本当にありがとうございました．

なので、シュレディンガー方程式の場合も別の（もっと条件の厳しい）境界を設定しないといけません．すぐ思いつくのは、Quiitaの式(3)に対してr→0の極限をとると、∂ψ+ψ=0の第三種境界条件がでることでしょうか．

— もしもし９ (@moshi_moshi_9) October 4, 2020

まとめると、ψで解く場合は第三種境界条件を使うべきである．Quiitaでは誤った境界条件に関する仮定から出発しているが、幸運にもほかの境界条件から導いた表式と同じものになっているため、厳密解に相当する答えが得られた．ということでしょうか．

— もしもし９ (@moshi_moshi_9) October 4, 2020

また、wakabame様のブログでも，原点での境界条件処理が不要なことについての証明がなされています．wakabame様，本当にありがとうございました．

波動関数を規格化（正規化）する

最後に、波動関数$ \psi(r) $を規格化（正規化）します．具体的には、

%
%TCIMACRO{\dint \nolimits_{0}^{r_{c}}}%
%BeginExpansion
{\displaystyle\int\nolimits_{0}^{r_{c}}}
%EndExpansion
r^{2}\psi^{\ast}\left(  r\right)  \psi\left(  r\right)  dr=1 \tag{25}

が満たされるように、$ \psi(r) $を定数倍します．これは、

A^{2}=%
%TCIMACRO{\dint \nolimits_{0}^{r_{c}}}%
%BeginExpansion
{\displaystyle\int\nolimits_{0}^{r_{c}}}
%EndExpansion
r^{2}\psi^{\ast}\left(  r\right)  \psi\left(  r\right)  dr \tag{26}

\psi\left(  r\right)  :=\dfrac{1}{A}\psi\left(  r\right) \tag{27}

とすることにより可能です．ここで、$ (26) $式は、数値積分によって求めなければなりません．

水素原子のs状態に対するSchrödinger方程式を，有限要素法で数値的に解くC++のプログラム

上述の方法によって，水素原子のs状態に対するSchrödinger方程式を，有限要素法で数値的に解くC++のプログラムは以下のようになります（多次元配列のためにBoost C++ Librariesを，また一般化固有値問題の解を求めるためにEigenをそれぞれ使っていますので，注意してください）．ただし，全部載せると非常に長くなってしまうので，一部だけを掲載しています．なお，完全なコードはGitHubのこちらで公開しています．

double Hydrogen_FEM::do_run()
{
    // 各種データの生成
    make_data();

    // 要素行列の生成
    make_element_matrix();

    // 全体行列を生成
    make_global_matrix();
    
    // 境界条件処理を行う
    boundary_conditions();

    // 一般化固有値問題を解く
    Eigen::GeneralizedSelfAdjointEigenSolver<Eigen::MatrixXd> es(hg_, ug_);

    // 固有ベクトル（波動関数）を取得
    phi_ = es.eigenvectors().col(0);

    // 固有ベクトル（波動関数）のN要素目を追加
    phi_.resize(NODE_TOTAL);

    // 固有ベクトル（波動関数）を規格化
    normalize();

    return es.eigenvalues();
}

void Hydrogen_FEM::boundary_conditions()
{
    // 左辺の全体行列のN行とN列を削る
    hg_.conservativeResize(hg_.rows() - 1, hg_.cols() - 1);

    // 右辺の全体行列のN行とN列を削る
    ug_.conservativeResize(ug_.rows() - 1, ug_.cols() - 1);
}

double Hydrogen_FEM::get_A_matrix_element(std::int32_t e, double le, std::int32_t p, std::int32_t q) const
{
    auto const ed = static_cast<double>(e);
    switch (p) {
    case 0:
        switch (q) {
        case 0:
            return 0.5 * le * (ed * ed + ed + 1.0 / 3.0) - le * le * (ed / 3.0 + 1.0 / 12.0);

        case 1:
            return -0.5 * le * (ed * ed + ed + 1.0 / 3.0) - le * le * (ed / 6.0 + 1.0 / 12.0);

        default:
            BOOST_ASSERT(!"heの添字が2以上！");
            return 0.0;
        }

    case 1:
        switch (q) {
        case 0:
            return -0.5 * le * (ed * ed + ed + 1.0 / 3.0) - le * le * (ed / 6.0 + 1.0 / 12.0);

        case 1:
            return 0.5 * le * (ed * ed + ed + 1.0 / 3.0) - le * le * (ed / 3.0 + 0.25);

        default:
            BOOST_ASSERT(!"heの添字が2以上！");
            return 0.0;
        }

    default:
        BOOST_ASSERT(!"heの添字が2以上！");
        return 0.0;
    }
}

double Hydrogen_FEM::get_B_matrix_element(std::int32_t e, double le, std::int32_t p, std::int32_t q) const
{
    auto const ed = static_cast<double>(e);
    switch (p) {
    case 0:
        switch (q) {
        case 0:
            return le * le * le * (ed * ed / 3.0 + ed / 6.0 + 1.0 / 30.0);

        case 1:
            return le * le * le * (ed * ed / 6.0 + ed / 6.0 + 0.05);

        default:
            BOOST_ASSERT(!"ueの添字が2以上！");
            return 0.0;
        }

    case 1:
        switch (q) {
        case 0:
            return le * le * le * (ed * ed / 6.0 + ed / 6.0 + 0.05);

        case 1:
            return le * le * le * (ed * ed / 3.0 + ed / 2.0 + 0.2);

        default:
            BOOST_ASSERT(!"ueの添字が2以上！");
            return 0.0;
        }

    default:
        BOOST_ASSERT(!"ueの添字が2以上！");
        return 0.0;
    }
}

void Hydrogen_FEM::make_element_matrix()
{
    // 各線分要素の長さを計算
    for (auto e = 0; e < ELE_TOTAL; e++) {
        length_[e] = std::fabs(node_r_ele_[e][1] - node_r_ele_[e][0]);
    }

    // 要素行列の各成分を計算
    for (auto e = 0; e < ELE_TOTAL; e++) {
        auto const le = length_[e];
        for (auto i = 0; i < 2; i++) {
            for (auto j = 0; j < 2; j++) {
                mat_A_ele_[e][i][j] = get_A_matrix_element(e, le, i, j);
                mat_B_ele_[e][i][j] = get_B_matrix_element(e, le, i, j);
            }
        }
    }
}

void Hydrogen_FEM::make_data()
{
    // Global節点のx座標を定義(R_MIN～R_MAX）
    auto const dr = (R_MAX - R_MIN) / static_cast<double>(ELE_TOTAL);
    for (auto i = 0; i <= ELE_TOTAL; i++) {
        // 計算領域を等分割
        node_r_glo_[i] = R_MIN + static_cast<double>(i) * dr;
    }

    for (auto e = 0; e < ELE_TOTAL; e++) {
        node_num_seg_[e][0] = e;
        node_num_seg_[e][1] = e + 1;
    }
    
    for (auto e = 0; e < ELE_TOTAL; e++) {
        for (auto i = 0; i < 2; i++) {
            node_r_ele_[e][i] = node_r_glo_[node_num_seg_[e][i]];
        }
    }
}

void Hydrogen_FEM::make_global_matrix()
{
    for (auto e = 0; e < ELE_TOTAL; e++) {
        for (auto i = 0; i < 2; i++) {
            for (auto j = 0; j < 2; j++) {
                hg_(node_num_seg_[e][i], node_num_seg_[e][j]) += mat_A_ele_[e][i][j];
                ug_(node_num_seg_[e][i], node_num_seg_[e][j]) += mat_B_ele_[e][i][j];
            }
        }
    }
}

void Hydrogen_FEM::normalize()
{
    auto sum = 0.0;
    auto const size = phi_.size();
    auto const max = size - 2;

    // Simpsonの公式によって数値積分する
    for (auto i = 0; i < max; i += 2) {
        auto const f0 = phi_[i] * phi_[i] * node_r_glo_[i] * node_r_glo_[i];
        auto const f1 = phi_[i + 1] * phi_[i + 1] * node_r_glo_[i + 1] * node_r_glo_[i + 1];
        auto const f2 = phi_[i + 2] * phi_[i + 2] * node_r_glo_[i + 2] * node_r_glo_[i + 2];
        sum += (f0 + 4.0 * f1 + f2);
    }
    
    auto const a_1 = 1.0 / std::sqrt(sum * length_[0] / 3.0);

    for (auto i = 0; i < size; i++) {
        phi_[i] *= -a_1;
    }
}

水素原子のs状態に対するSchrödinger方程式を，有限要素法で数値的に解くJuliaのプログラム

C++のプログラムがあまりに遅いので、同様のプログラムをJuliaに移植してみました．Julia版の方が12倍くらい速いので、こちらを推奨します（なお、C++版の方も、EigenからLAPACK/BLASを呼び出すようにすれば、Julia版と同等の速度が出ます）．ただし，全部載せると非常に長くなってしまうので，一部だけを掲載しています．なお，完全なコードはGitHubのこちらで公開しています．

function do_run(param, val)
    # データの生成
    make_data!(param, val)

    # 要素行列の生成
    make_element_matrix!(param, val)

    # 全体行列を生成
    hg_tmp, ug_tmp = make_global_matrix(param, val)

    # 境界条件処理を行う
    boundary_conditions!(param, val, hg_tmp, ug_tmp)

    # 一般化固有値問題を解く
    eigenval, phi = eigen(val.hg, val.ug)
    
    # s状態の固有ベクトルを取り出す
    val.phi = @view(phi[:,1])

    # 固有ベクトルの要素数を増やす
    resize!(val.phi, NODE_TOTAL)

    # 固有ベクトル（波動関数）を規格化
    normalize!(val)

    return eigenval
end

function boundary_conditions!(param, val, hg_tmp, ug_tmp)
    @inbounds for i = 1:param.ELE_TOTAL
        for j = i - 1:i + 1
            if j != 0 && j != param.NODE_TOTAL
                # 左辺の全体行列のN行とN列を削る
                val.hg.data[j, i] = hg_tmp.data[j, i]

                # 右辺の全体行列のN行とN列を削る    
                val.ug.data[j, i] = ug_tmp.data[j, i]
            end
        end
    end
end

get_A_matrix_element(e, le, p, q) = let
    ed = float(e - 1);
    @match p begin
        1 =>
            @match q begin
                1 => return  0.5 * le * (ed * ed + ed + 1.0 / 3.0) - le * le * (ed / 3.0 + 1.0 / 12.0);
                2 => return -0.5 * le * (ed * ed + ed + 1.0 / 3.0) - le * le * (ed / 6.0 + 1.0 / 12.0);
                _ => return 0.0
            end

        2 =>
            @match q begin
                1 => return -0.5 * le * (ed * ed + ed + 1.0 / 3.0) - le * le * (ed / 6.0 + 1.0 / 12.0);
                2 => return 0.5 * le * (ed * ed + ed + 1.0 / 3.0) - le * le * (ed / 3.0 + 0.25);
                _ => return 0.0
            end

        _ => return 0.0
    end
end

get_B_matrix_element(e, le, p, q) = let
    ed = float(e - 1);
    @match p begin 
        1 =>
            @match q begin
                1 => return le * le * le * (ed * ed / 3.0 + ed / 6.0 + 1.0 / 30.0);
                2 => return le * le * le * (ed * ed / 6.0 + ed / 6.0 + 0.05);
                _ => return 0.0
            end

        2 =>
            @match q begin
                1 => return le * le * le * (ed * ed / 6.0 + ed / 6.0 + 0.05);
                2 => return le * le * le * (ed * ed / 3.0 + ed / 2.0 + 0.2);
                _ => return 0.0
            end
        
        _ => return 0.0
    end
end

function make_data(param, val)
    # Global節点のx座標を定義(R_MIN～R_MAX）
    dr = (param.R_MAX - param.R_MIN) / float(param.ELE_TOTAL);
    for i = 0:param.NODE_TOTAL - 1
        # 計算領域を等分割
        val.node_r_glo[i + 1] = param.R_MIN + float(i) * dr;
    end

    for e = 1:param.ELE_TOTAL
        val.node_num_seg[e, 1] = e;
        val.node_num_seg[e, 2] = e + 1;
    end
        
    for e = 1:param.ELE_TOTAL
        for i = 1:2
            val.node_r_ele[e, i] = val.node_r_glo[val.node_num_seg[e, i]];
        end
    end
end

function make_element_matrix(param, val)
    # 各線分要素の長さを計算
    for e = 1:param.ELE_TOTAL
        val.length[e] = abs(val.node_r_ele[e, 2] - val.node_r_ele[e, 1]);
    end

    # 要素行列の各成分を計算
    for e = 1:param.ELE_TOTAL
        le = val.length[e];
        for i = 1:2
            for j = 1:2
                val.mat_A_ele[e, i, j] = get_A_matrix_element(e, le, i, j);
                val.mat_B_ele[e, i, j] = get_B_matrix_element(e, le, i, j);
                end
            end
        end
    end
end

function make_global_matrix(param, val)
    hg_tmp = Symmetric(zeros(param.NODE_TOTAL, param.NODE_TOTAL))
    ug_tmp = Symmetric(zeros(param.NODE_TOTAL, param.NODE_TOTAL))

    for e = 1:param.ELE_TOTAL
        for i = 1:2
            for j = 1:2
                hg_tmp.data[val.node_num_seg[e, i], val.node_num_seg[e, j]] += val.mat_A_ele[e, i, j]
                ug_tmp.data[val.node_num_seg[e, i], val.node_num_seg[e, j]] += val.mat_B_ele[e, i, j]
            end
        end
    end

    return hg_tmp, ug_tmp
end

function normalize!(val)
    sum = 0.0
    len = length(val.phi)
    max = len - 2

    # Simpsonの公式によって数値積分する
    @inbounds @simd for i = 1:2:max
        f0 = val.phi[i] * val.phi[i] * val.node_r_glo[i] * val.node_r_glo[i]
        f1 = val.phi[i + 1] * val.phi[i + 1] * val.node_r_glo[i + 1] * val.node_r_glo[i + 1]
        f2 = val.phi[i + 2] * val.phi[i + 2] * val.node_r_glo[i + 2] * val.node_r_glo[i + 2]
        
        sum += (f0 + 4.0 * f1 + f2)
    end
    
    val.phi .*= (-1.0 / sqrt(sum * val.length[1] / 3.0))
end

なお，これらのプログラムは，@Sunset_Yuhi様のこちらの記事の，fem1d_poisson01.pyを参考にさせて頂きました．

有限要素法のプログラムによる水素原子の基底状態のエネルギーの計算結果の結果と考察

ここで，この有限要素法のプログラムによる$ N = 100 $，$ N = 500 $，$ N = 1000 $，$ N = 5000 $のときのエネルギーの計算結果（ただし，$ r_{c} = 30 (a.u.) $）を表に示しますと，以下のようになります（単位は全てHartree原子単位です）．

N	s状態のエネルギー
100	-0.496368
500	-0.499845
1000	-0.499962
5000	-0.499998
厳密	-0.500000

表から分かるとおり，$ N $が大きくなるほど厳密な値に近づいていることが分かります． 特に，$ N = 5000 $の時は，厳密な値の99.9996％のエネルギーを与え，非常に良好な結果となっています．

有限要素法のプログラムによる水素原子のエネルギー固有値と厳密なエネルギー固有値の比較

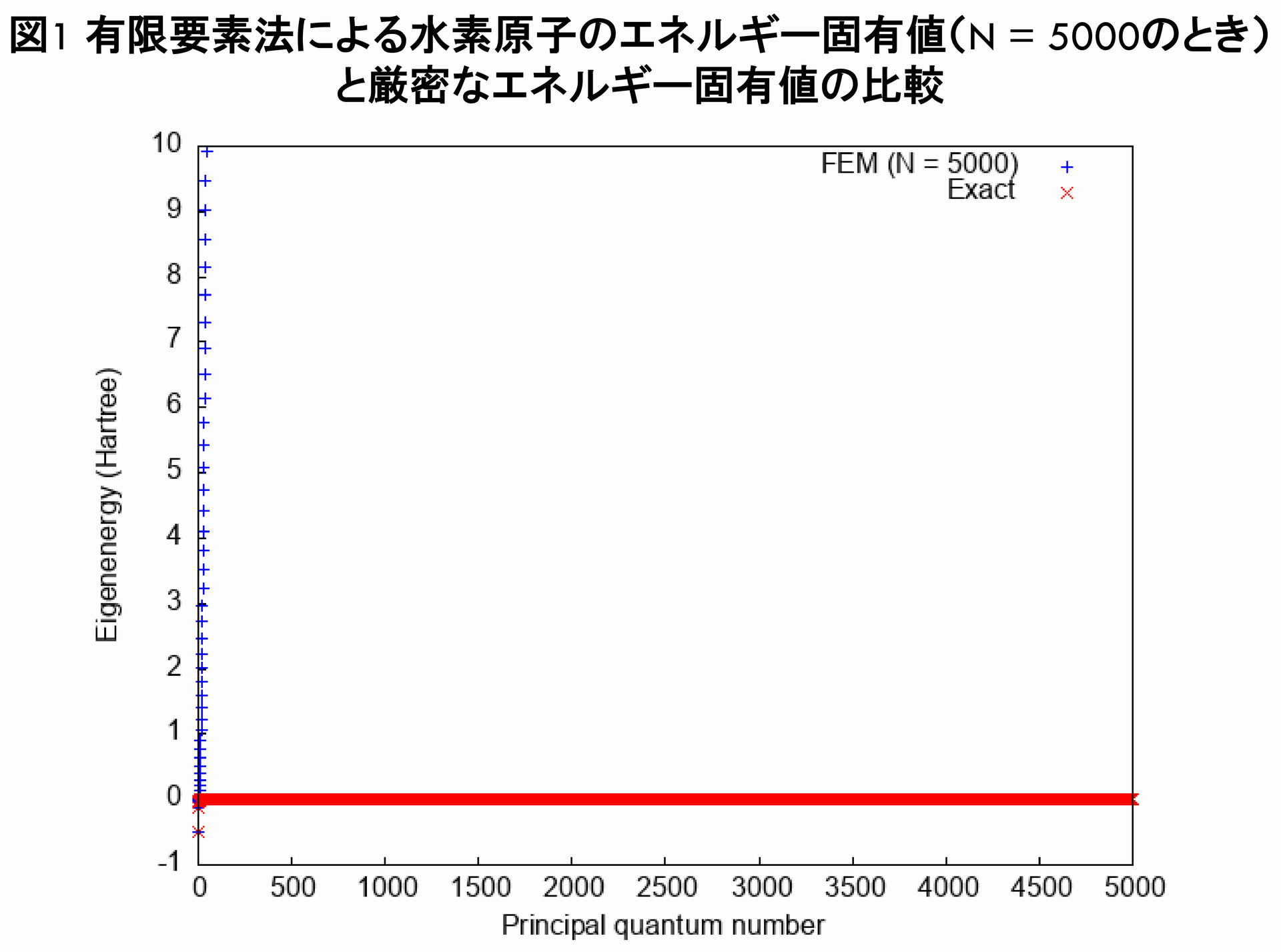
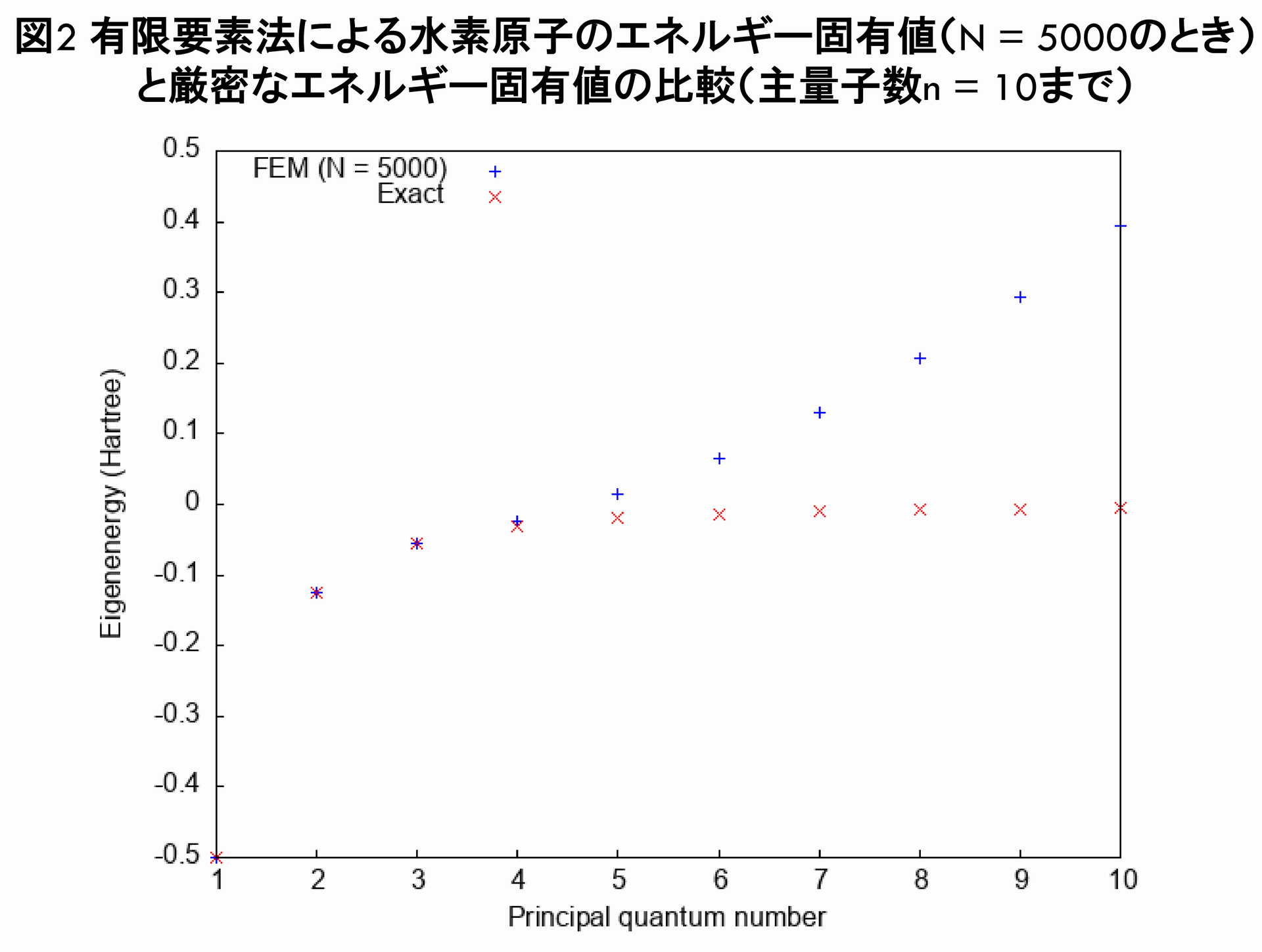
続いて，この有限要素法のプログラムによる水素原子のエネルギー固有値（$ N = 5000 $のとき）と厳密なエネルギー固有値とを，プロットで比較してみることにしましょう．

図1の通り、有限要素法のプログラムによる水素原子のエネルギー固有値は、厳密なエネルギー固有値を全く再現していないことが分かります．ただし図2を見ると，どうやら主量子数$ n = 3 $までは，厳密なエネルギー固有値を再現しているらしいことが分かります．

@cometscome_physさんから，以下のようなツイートを頂きました．

原因がわかりました。rc=30が小さすぎます。差分化でrc=30で有限要素法とほぼ同じ結果になりました。rcを大きくしていくと厳密解に近づいていきます

— Yuki Nagai (@cometscome_phys) March 7, 2021

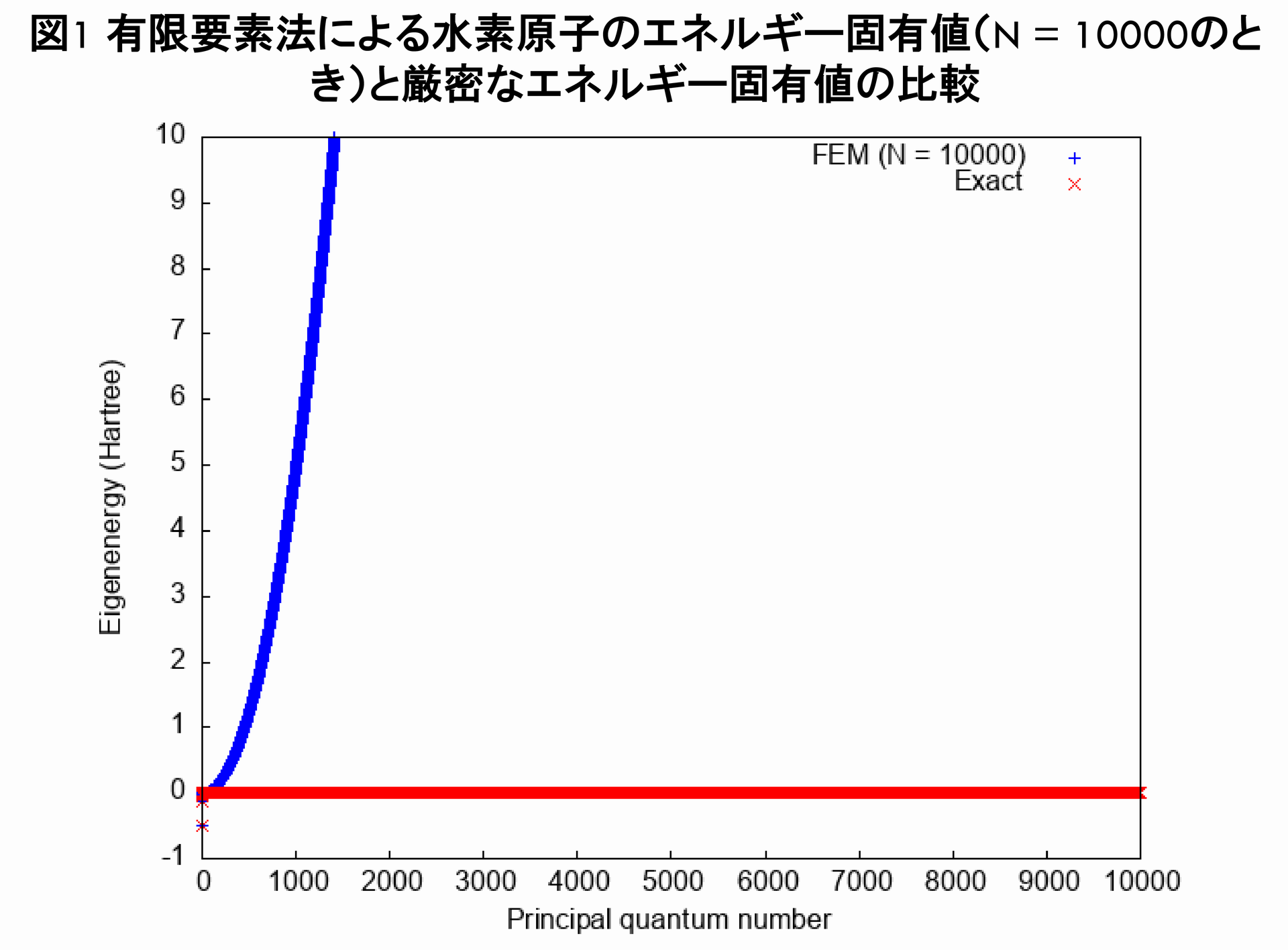
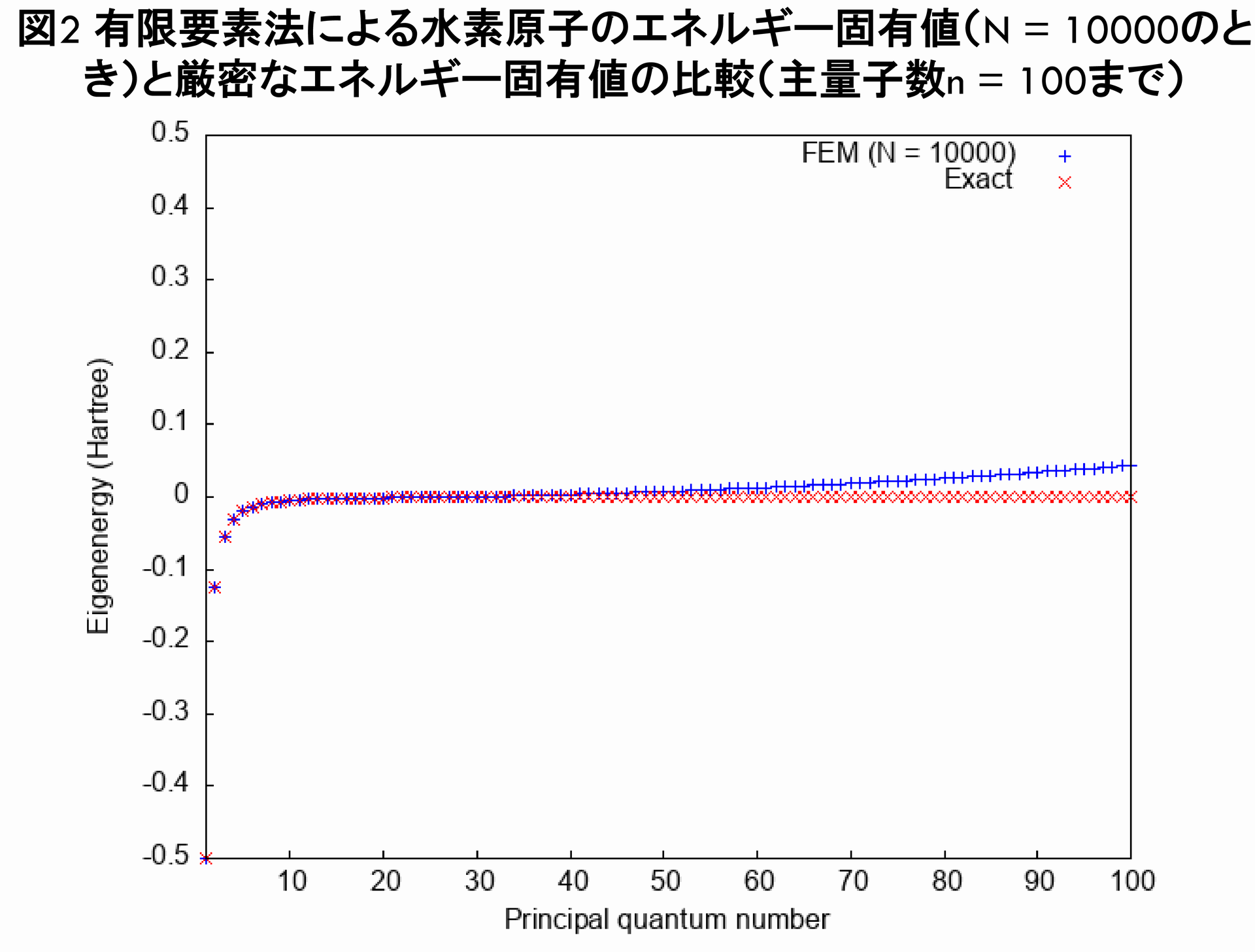
従って，$ r_c = 30.0(a.u.) $から$ r_c = 1000.0(a.u.) $に変更して計算し直したら（ついでに$ N = 10000 $に増やしました），以下の図1，図2のような結果が得られました．図2を見ると，どうやら主量子数$ n = 30 $くらいまでは，厳密なエネルギー固有値を再現しているらしいことが分かります．

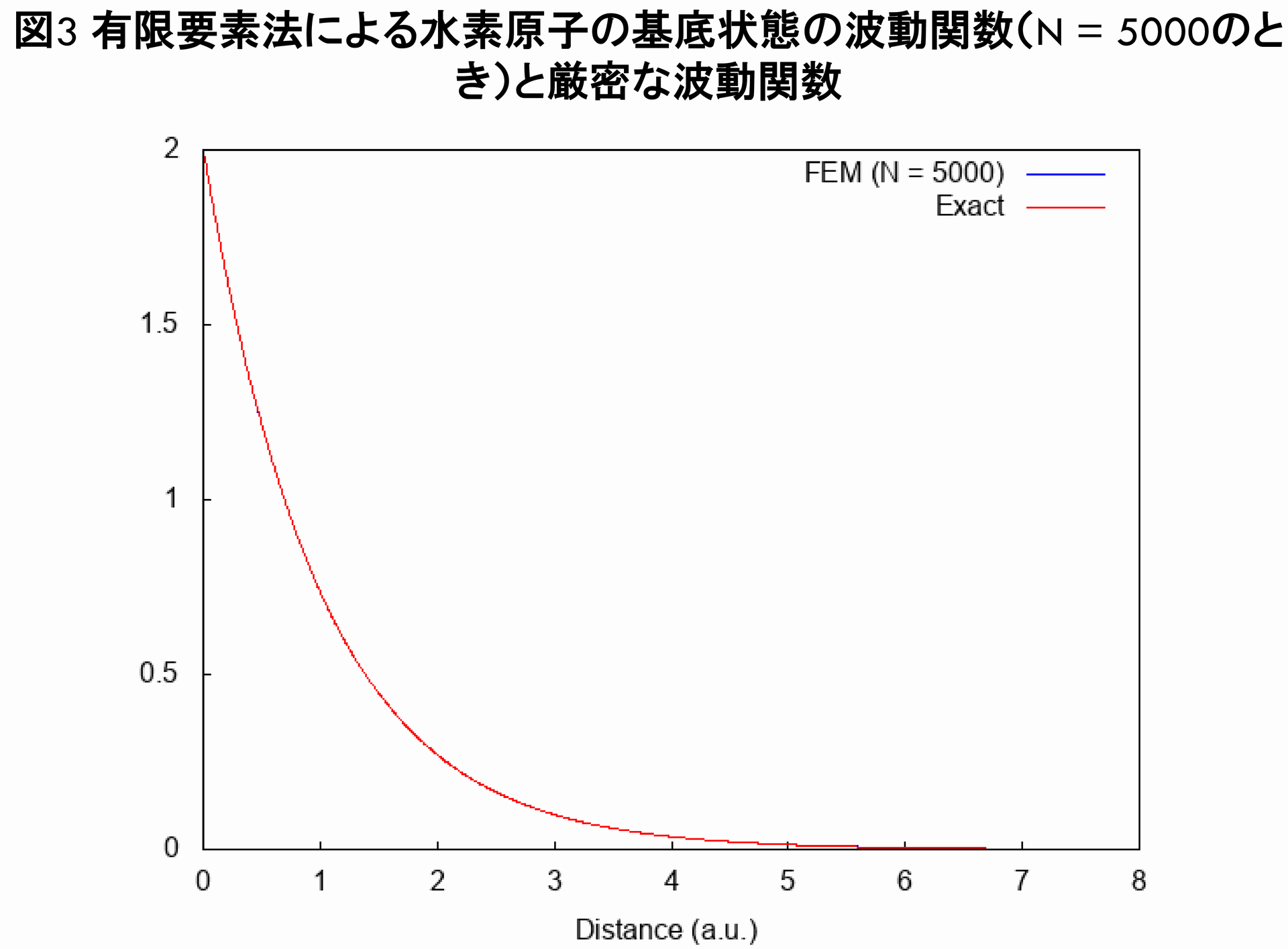
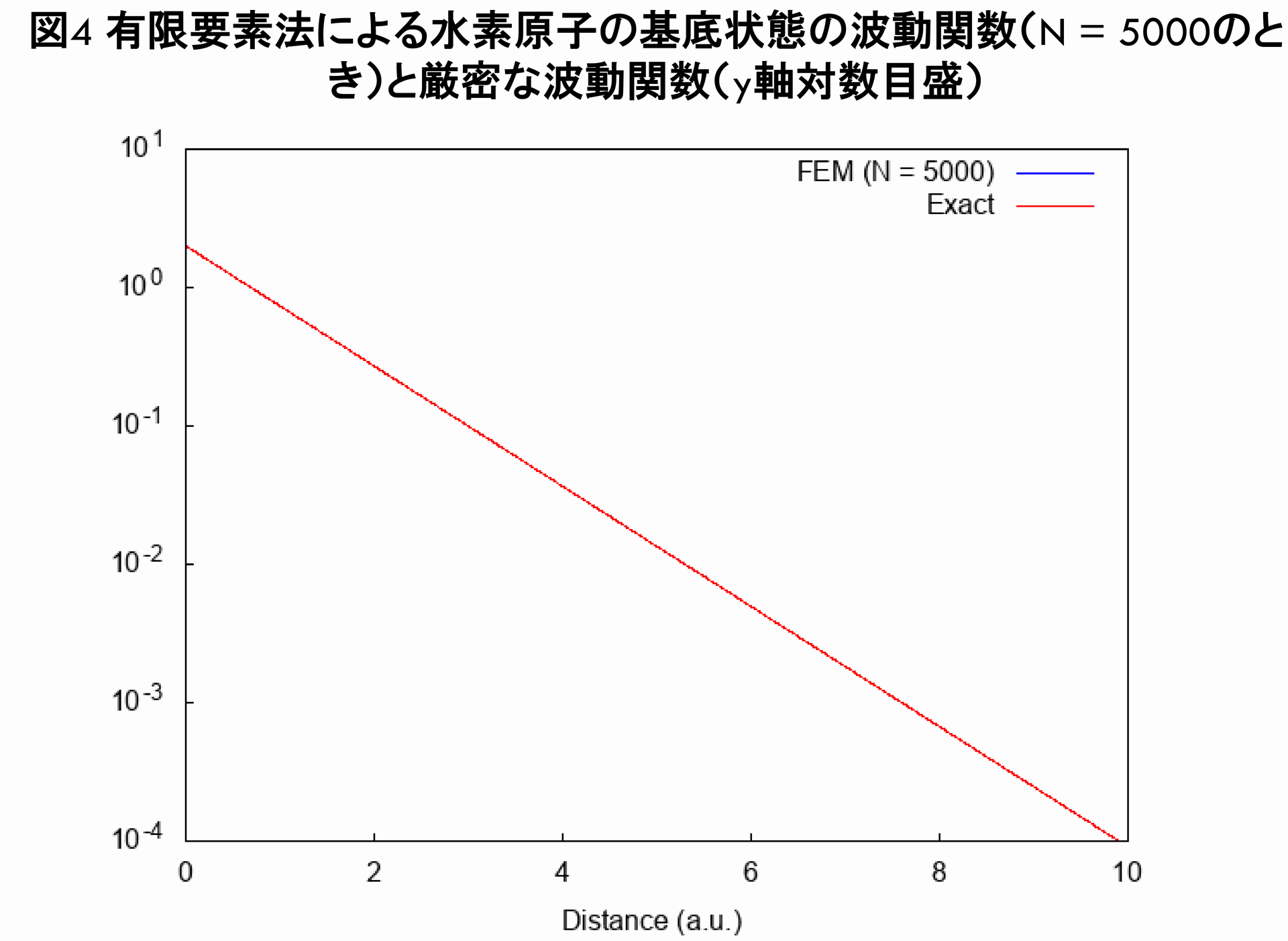
有限要素法のプログラムによる水素原子の基底状態の波動関数と厳密な波動関数との比較

続いて，この有限要素法のプログラムによる水素原子の基底状態の波動関数（$ N = 5000 $のとき）と厳密な波動関数とを，プロットで比較してみることにしましょう．

ここで，図3は普通の目盛，図4はy軸対数目盛となっていることに注意してください．図1，図2の通り，有限要素法による水素原子の基底状態の波動関数と厳密な波動関数は，プロットでは完全に一致しており，非常に良好な結果と言えます．

まとめ

1. 水素原子のs状態に対するSchrödinger方程式を弱形式にする方法を説明しました．
2. 弱形式からローカル行列を生成し，ローカル行列の行列方程式から全体行列の行列方程式を求める方法について説明しました．
3. 全体行列の行列方程式が，一般化固有値問題に帰着することを説明しました．
4. 全体行列の境界条件処理について説明しました．
5. 工程2.～4.と一般化固有値問題を解き、その解である波動関数を正規化するC++プログラムおよびJuliaプログラムを紹介しました．
6. 有限要素法のプログラムによる水素原子のエネルギー固有値と厳密なエネルギー固有値の比較を行いました．
7. 有限要素法のプログラムによる水素原子の基底状態の波動関数と厳密な波動関数との比較を行いました．

参考サイト

[1] Pythonで有限要素法（1次元Poisson方程式）

参考文献

1. 日本計算工学会編『計算力学（第2版）』森北出版（2012） ↩

2. 菊地文雄『有限要素法概説―理工学における基礎と応用』サイエンス社（1999） ↩

3. L. R. Ram‐Mohan, S. Saigal, D. Dossa, and J. Shertzer, Computers in Physics 4, 50 (1990). ↩