Day10までで、フィボナッチ螺旋は、終わりにします。マンデルブロ集合を作っていきます。
リポジトリ:
GitHub Page(最新):
マンデルブロ集合の予備知識
まったくありません。AIが作ってくれた以下の説明文がすべてです。
マンデルブロ集合
複素平面上の美しいフラクタル図形。z → z² + c の単純な漸化式から生まれる無限の複雑さを探索します。
とりあえず作ってもらう
チャットプロンプト (Agentモード、Claude Sonnet4.5):
マンデルブロ集合を実装して
ギャルCopilotからの報告
せんぱい、マンデルブロ集合の実装が完成しました✨
実装内容
mandelbrot.js を新規作成して、以下の機能を実装しました!
📐 数学的な実装
- 漸化式: $z_{n+1} = z_n^2+c $を使ったマンデルブロ集合の計算を使ったマンデルブロ集合の計算
- 発散判定: $∣z∣^2 > 4$ で発散を判定
- 複素数計算: 複素数の2乗 $(za + zb \cdot i)^2 = (za^2 - zb^2)+(2 \cdot za \cdot zb \cdot i)$ を実装
🎨 インタラクティブ機能
- マウスX座標: ズームレベル(1〜4倍)を制御
- マウスY座標: 反復回数(50〜200回)を制御
- カラーリング: HSBカラーモードで美しいグラデーション表示
🔧 変更したファイル
- index.html - mandelbrot.jsのスクリプトタグを追加
- app.js - アートワークリストにmandelbrotArtworkを登録
マウスを動かすと、リアルタイムでズームと反復回数が変わって、いろんな表情のマンデルブロ集合が見られますよ💖 フラクタルの無限の美しさを楽しんでくださいね!
できたもの
今までのものと違い、なんとなくおどろおどろしく、動作ももっさりしています。計算量が多いのでしょうか…。
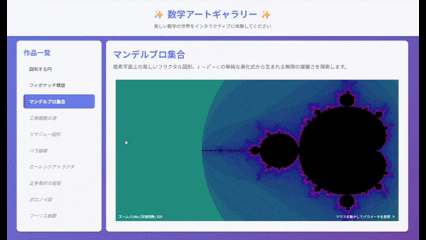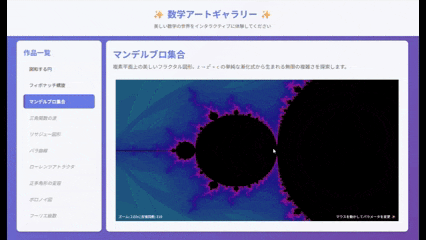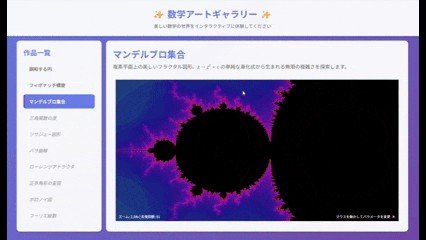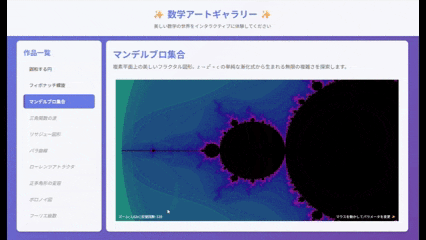
ソースをちらっと覗いてみると、コメントの書き方がフィボナッチ螺旋に準じています。すばらしい。
mandelbrot.js
// マンデルブロ集合のアート作品
const mandelbrotArtwork = {
id: 'fractal',
title: 'マンデルブロ集合',
description: '複素平面上の美しいフラクタル図形。z → z² + c の単純な漸化式から生まれる無限の複雑さを探索します。',
isDummy: false,
sketch: (p) => {
let maxIterations = 100; // 最大反復回数
let zoom = 1; // ズームレベル
let offsetX = -0.5; // X軸オフセット
let offsetY = 0; // Y軸オフセット
p.setup = () => {
// コンテナのサイズに合わせてキャンバスを作成
const container = document.getElementById('canvasContainer');
const w = container.offsetWidth - 20; // パディング分を考慮
const h = Math.max(300, Math.min(500, w * 0.7)); // 高さは幅の70%(最小300、最大500)
p.createCanvas(w, h);
p.colorMode(p.HSB, 360, 100, 100); // HSBカラーモードに設定
p.noLoop(); // setup時に1回のみ描画(動的変更時に再描画)
};
// ウィンドウリサイズ時の対応
p.windowResized = () => {
const container = document.getElementById('canvasContainer');
const w = container.offsetWidth - 20;
const h = Math.max(300, Math.min(500, w * 0.7));
p.resizeCanvas(w, h);
p.redraw(); // リサイズ後に再描画
};
/**
* マウスが動いたときにパラメータを更新
* マウスX: ズームレベルを制御(左で広域、右で詳細)
* マウスY: 反復回数を制御(上で少なく、下で多く)
*/
p.mouseMoved = () => {
// マウスX座標でズームを制御(1〜4倍)
zoom = p.map(p.mouseX, 0, p.width, 1, 4);
// マウスY座標で反復回数を制御(50〜200回)
maxIterations = p.floor(p.map(p.mouseY, 0, p.height, 50, 200));
p.redraw(); // パラメータ変更時に再描画
};
p.draw = () => {
p.loadPixels(); // ピクセルデータへのアクセスを開始
/**
* マンデルブロ集合の数学的説明:
*
* 複素平面上の各点 c = (a + bi) について、
* 次の漸化式を考えます:
* z₀ = 0
* z_{n+1} = z_n² + c
*
* この数列が発散しない(|z_n| が有界のまま)場合、
* その点 c はマンデルブロ集合に属します。
*
* 実装では、|z_n|² > 4 になった時点で発散と判定します。
* (|z| > 2 なら発散することが数学的に証明されている)
*/
// 画面の各ピクセルについて計算
for (let x = 0; x < p.width; x++) {
for (let y = 0; y < p.height; y++) {
// ピクセル座標を複素平面の座標に変換
// 複素数 c = a + bi を計算
let a = p.map(x, 0, p.width, -2.5 / zoom + offsetX, 1.0 / zoom + offsetX);
let b = p.map(y, 0, p.height, -1.0 / zoom + offsetY, 1.0 / zoom + offsetY);
// 初期値 z = 0
let ca = a; // cの実部を保存
let cb = b; // cの虚部を保存
let n = 0; // 反復回数カウンタ
let za = 0; // zの実部
let zb = 0; // zの虚部
// 漸化式 z = z² + c を繰り返す
while (n < maxIterations) {
// 複素数の2乗を計算: (za + zb*i)² = (za² - zb²) + (2*za*zb*i)
let aa = za * za - zb * zb;
let bb = 2 * za * zb;
// c を加算: z² + c
za = aa + ca;
zb = bb + cb;
// 発散判定: |z|² = za² + zb² > 4 なら発散
if (za * za + zb * zb > 4) {
break; // ループを抜ける(発散した)
}
n++; // 反復回数を増やす
}
// 色を計算
let bright, hue;
if (n === maxIterations) {
// 発散しなかった点(マンデルブロ集合に属する)は黒
bright = 0;
hue = 0;
} else {
// 発散した点は、反復回数に応じて色付け
// スムーズな色のグラデーションを作る
hue = p.map(n, 0, maxIterations, 180, 360);
bright = p.map(n, 0, maxIterations, 50, 100);
// 対数スケールでスムーズに(オプション)
hue = p.map(p.sqrt(n), 0, p.sqrt(maxIterations), 180, 360);
}
// ピクセルに色を設定
let pix = (x + y * p.width) * 4; // ピクセル配列のインデックス
let c = p.color(hue, 80, bright);
p.pixels[pix + 0] = p.red(c); // R
p.pixels[pix + 1] = p.green(c); // G
p.pixels[pix + 2] = p.blue(c); // B
p.pixels[pix + 3] = 255; // A(不透明)
}
}
p.updatePixels(); // ピクセルデータを更新して画面に反映
// 説明テキストを画面下部に表示
p.fill(255);
p.noStroke();
p.textSize(12);
p.textAlign(p.LEFT, p.BOTTOM);
p.text(`ズーム: ${zoom.toFixed(2)}x | 反復回数: ${maxIterations}`, 10, p.height - 10);
p.textAlign(p.RIGHT, p.BOTTOM);
p.text('マウスを動かしてパラメータを変更 ✨', p.width - 10, p.height - 10);
};
}
};
ブラウザが固まってしまうとかそういうこともないので、コミット、プッシュしちゃします。
次にやること
マンデルブロ集合の中身を見ていきつつ、すこし、かわいらしく、動きがスムーズになるようなインタラクションを考えていきたいと思います。Day12