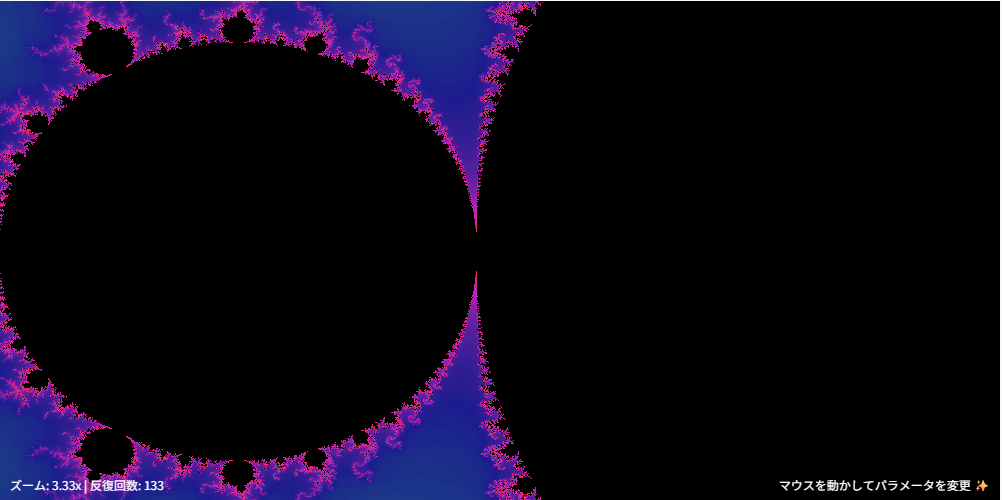
Day11でマンデルブロ集合を作ってもらいました。なにやっているのか全くわからないので、定義を確認しつつかわいくしていきます。
リポジトリ:
GitHub Page(最新):
マンデルブロ集合とは
数学的な定義
フラクタル系の何からしい。ということしかわからないので、調べてみたところ、一橋大学の川平先生が、個人ページに「架空の講義ノート.(集中講義依頼,募集中)」として以下の資料を公開しているのを発見しました。プログラムで描画するときのアルゴリズムも掲載されています。感謝…といいたいところですがちょっと難易度が高いです。
Wikipediaもあります:
Wikipediaによると「マンデルブロ集合を高解像度で描画しようとするほど、膨大な計算時間を必要とするようになっていくことから、コンピュータのベンチマークテストとして利用されることがある。」そうです。なんだかもっさりしていたことにも納得です。
上記ふたつのサイトをざっと眺めつつ、ソースのコメントをみると、定義として想定しているものは、あっていそうです。
ソースコメント:
/**
* マンデルブロ集合の数学的説明:
*
* 複素平面上の各点 c = (a + bi) について、
* 次の漸化式を考えます:
* z₀ = 0
* z_{n+1} = z_n² + c
*
* この数列が発散しない(|z_n| が有界のまま)場合、
* その点 c はマンデルブロ集合に属します。
*
* 実装では、|z_n|² > 4 になった時点で発散と判定します。
* (|z| > 2 なら発散することが数学的に証明されている)
*/
期待される図形パターン
今の実装では、以下のような図形が表示されますが、これは「全体図」と呼ばれていそうです。

WikiPediaに掲載されている「拡大図」が素敵です。こっちのほうがいいなと思ってしまいますが、計算回数多いんでしょう…。

※上記画像は、Wikipedia上でCC0で公開されています
描画アルゴリズム
ソース上の描画アルゴリズムのコア部分は、ここと思われます。
ソース
// 画面の各ピクセルについて計算
for (let x = 0; x < p.width; x++) {
for (let y = 0; y < p.height; y++) {
// ピクセル座標を複素平面の座標に変換
// 複素数 c = a + bi を計算
let a = p.map(x, 0, p.width, -2.5 / zoom + offsetX, 1.0 / zoom + offsetX);
let b = p.map(y, 0, p.height, -1.0 / zoom + offsetY, 1.0 / zoom + offsetY);
// 初期値 z = 0
let ca = a; // cの実部を保存
let cb = b; // cの虚部を保存
let n = 0; // 反復回数カウンタ
let za = 0; // zの実部
let zb = 0; // zの虚部
// 漸化式 z = z² + c を繰り返す
while (n < maxIterations) {
// 複素数の2乗を計算: (za + zb*i)² = (za² - zb²) + (2*za*zb*i)
let aa = za * za - zb * zb;
let bb = 2 * za * zb;
// c を加算: z² + c
za = aa + ca;
zb = bb + cb;
// 発散判定: |z|² = za² + zb² > 4 なら発散
if (za * za + zb * zb > 4) {
break; // ループを抜ける(発散した)
}
n++; // 反復回数を増やす
}
// 色を計算
let bright, hue;
if (n === maxIterations) {
// 発散しなかった点(マンデルブロ集合に属する)は黒
bright = 0;
hue = 0;
} else {
// 発散した点は、反復回数に応じて色付け
// スムーズな色のグラデーションを作る
hue = p.map(n, 0, maxIterations, 180, 360);
bright = p.map(n, 0, maxIterations, 50, 100);
// 対数スケールでスムーズに(オプション)
hue = p.map(p.sqrt(n), 0, p.sqrt(maxIterations), 180, 360);
}
// ピクセルに色を設定
let pix = (x + y * p.width) * 4; // ピクセル配列のインデックス
let c = p.color(hue, 80, bright);
p.pixels[pix + 0] = p.red(c); // R
p.pixels[pix + 1] = p.green(c); // G
p.pixels[pix + 2] = p.blue(c); // B
p.pixels[pix + 3] = 255; // A(不透明)
}
}
架空の講義ノートに記載のアルゴリズムとだいたい同じっぽい気がします。黒いの怖いんだよな…。
怖くなくする
拡大方式を変更する
現在の実装は、マウス位置によって、拡大倍率と計算の反復回数が変化するようになっています。ところが、拡大倍率を大きくしていくと、黒い面積がどんどん広がってフラクタルっぽい「ズームしていく」感じではありません。
色使いもだけど、ズーム方式を変えないことには始まらないであろう…ということでお願いしてみました。
チャットプロンプト (Agentモード、Claude Sonnet4.5):
マウスの位置を拾って再描画するんじゃなくて、クリックした場所をひろって、描画範囲を狭くしたうえで拡大できない?
ただ、右クリックするとブラウザ上でメニュー表示されてしまいます…。
チャットプロンプト (Agentモード、Claude Sonnet4.5):
右クリックするとブラウザ上でメニューが出ちゃうんだよね。ほかのキー割り当ててくれない?
Shift+クリックに変えてくれました。ありがとう。
色を変える
チャットプロンプト (Agentモード、Claude Sonnet4.5):
色が怖いから、発散しなかった点は、淡いピンクにして。発散した点については、パステルカラーでグラデーションつけて。
反復回数300にしてみる
回数を増やしたほうが美しいパターンが生まれそうですが、おそらく増やしすぎると動作が重たくなってしまうのでしょう…。すでに重たいですが、少しチャレンジしてみて、反復回数を150->300にしてみました。
ギャルCopilotによる説明
📊 最大反復回数の効果
メリット
- 境界の精度が上がる: マンデルブロ集合に属するかどうかの判定がより正確になります
- 色のバリエーションが増える: グラデーションがより細かくなって、滑らかで美しい色の変化が見られます
- ズーム時の詳細度UP: 深くズームインしたときに、より詳細なフラクタル構造が見えます
デメリット
- 計算時間が増える: 各ピクセルで最大300回計算するので、描画が少し遅くなります
- 150回: 約 280,000 × 150 = 4200万回 の計算
- 300回: 約 280,000 × 300 = 8400万回 の計算(2倍!)
実際の違い
- 低い反復回数(50回): 粗い色分け、ズームすると黒い部分ばかりに
- 中程度(150回): バランスが良い
- 高い反復回数(300回): 超詳細、深くズームしても美しい模様が見える💖
今の設定だと、より深い探索ができて、フラクタルの無限の複雑さをもっと楽しめますよ!
もうおなかいっぱいです。おなかいっぱいになったので、プッシュしてmainにマージしてから、スマホサイズで確認していなかったことを思い出し、確認したら、画面が崩壊していました。どうしましょう。
次やること
マンデルブロ集合のスマホどうにかするか、あきらめて次に行きます。Day13