TensorFlowを使って、点列を補間するベジェ曲線を求める（その１） #TensorFlow

TensorFlowは、とても柔軟性にとんだフレームワークだが、APIの情報があまり充実しているとは思えないために、慣れないと靴の上から足を掻く感が否めない。APIに慣れるためには、結局、それを使い倒すしかない。うまいことに、TensorFlowはニューラルネットワークの演算に限らず、他の目的でも使用できる汎用性を持っている（実用的かどうかはともかくとして）。それを利用して、APIに慣れるためのプログラム例がいくつも公開されているが、これもその一つである。

ここでやることは、「データ点を補間するベジェ曲線を求める」という、ある意味でつまらないことである。しかし、このアルゴリズムは機械学習のアルゴリズムと良く似ている。そして、機械学習と違って誰にでも分かるシンプルな目的であるために、逆に、APIを理解するのには適しているのではないだろうか。解法の必要のために、複数のtf.Graphを使用したことは、TensorFlowシステムの理解に役立つだろう。また、Optimizerにおける学習係数の役割についても、一定の示唆を与えることが出来た。最後に、計算結果の可視化についても説明する。

最初に、ここで使用しているTensorFlowのPythonクラスと関数を提示しておく。なお、tf.placeholderは次の記事（その２）で初めて登場する。

tf.Graph (メソッド: as_default(),finalize())
tf.Operator
tf.Tensorインライン数式
tf.Variable
tf.train.GradientDescentOptimizer (メソッド: minimize())
tf.Session (メソッド: run())
tf.placeholder()
tf.constant()
tf.matmul()
tf.reduce_mean()
tf.square()
tf.pack()
tf.initialized_all_variables()
tf.train.SummaryWriter (メソインライン数式ッド: add_summary())
tf.scaler_summary()
tf.merge_all_summaries()

APIについて詳しい情報が必要な方は、TensorFlow Python referenceを参照して頂きたい。

テーマ

ベジェ曲線による補間

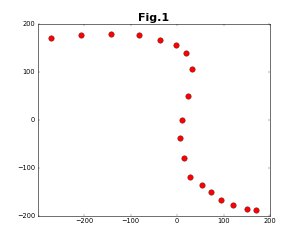
テーマは、与えられた2次元の点列を保管する3次のベジェ曲線を求める、というものである（このテーマ自体は、あまり万人に役に立つというものではない）。次のような点列を与えたと仮定する。

3次のベジェ曲線は次のように表される。

\boldsymbol{r}(t) = \sum_{k=0}^{3} f_k(t) \boldsymbol{b}_k　\tag{1}

f_k(t) =
\left(
\begin{matrix}
3 \\
k
\end{matrix}
\right)
t^k(1 - t)^{3-k} \tag{2}

ここで、$\boldsymbol{b}_k$は制御点であり、$t$は媒介変数である。3次のベジェ曲線では4点の制御点がある。点列を補間するベジェ曲線を求めることは、4点の制御点を求めることに他ならない。

補間曲線と点列との距離

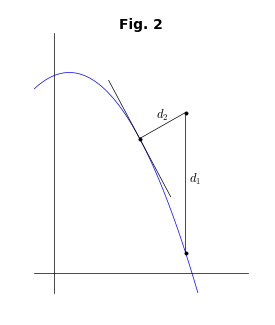
通常の最小二乗法では、補間曲線の確かさ（正確に言えば不確かさ）を表す量としての距離の二乗和の平均は、次のように表される。

D_1 = \frac{1}{N}\sum_{i=1}^N |f(x_i) - y_i|^2 \tag{3}

ここで、$y=f(x)$が補間曲線であり、$\{(x_i,y_i):i=1,N\}$はデータ点列である。実験データなどではx軸とy軸が異なる物理量であるから、これは妥当な考え方である。ところが、いま考えているような２次元平面ではｘ軸もｙ軸も同じ意味を持つため、補間曲線とデータ点の距離は、次のように表す方が適当である。

D_2 = \frac{1}{N}\sum_{i=1}^N \{(x(t_i) - x_i)^2 + (y(t_i) - y_i)^2\} \tag{4}

ここで、$(x(t),y(t))$は媒介変数$t$で表した補間曲線である（「媒介変数」と「パラメータ」は同じ意味だが、後で最適化パラメータが出てくるので、区別のために、ここでは「媒介変数」という表現を使う）。下図を見れば、2種類の距離の定義の違いは明らかであろう。

ところが、$D_2$の定義には問題がある。それは、補間曲線の法線上にデータ点が来るように媒介変数$t$を決めなければならないことである。3次のベジェ曲線の場合は、これは$t$についての5次方程式になってしまうため、解析的には解けない。

実装１

TensorFlowを使ってやりたいこと

TensorFlowでは、ニューラルネットワークの学習のために、目的関数の最小値を求める。その場合に使われる代表的な目的関数は、与えられた教師データに対して得られた試行結果と正しい結果との差の二乗平均である。言わば、どれだけ不正確かという因子であるから、損失関数と呼ばれる。その場合の最適化パラメータは相関の重み因子等々である

今回のテーマでは、$D_2$を目的関数にとる。最適化パラメータは制御点$\boldsymbol{b}_k$である。

D_2 = \frac{1}{N}\sum_{i=1}^N \{(x(t_i;\{\boldsymbol{b}_k\}) - x_i)^2 + (y(t_i;\{\boldsymbol{b}_k\}) - y_i)^2\} \tag{5}

上述のように、$D_2$の定義では媒介変数の列$\{t_i\}$を解析的に決めることができない。この困難を乗り越えるため、$\{t_i\}$も最適化パラメータにしてしまう。$D_2$が最小になるように${t_i}$を選べば、$(x(t_i;\{\boldsymbol{b}_k\}),y(t_i;\{\boldsymbol{b}_k\}))$は自動的に、データ点$(x_i,y_i)$から補間曲線に下ろした法線の足になるはずである。

【最適化パラメータ】

$\{\boldsymbol{b}_k:k=0,3\}$
$\{t_i:i=0,N-1\}$

Pythonコード

この方法で最適化を行う関数を以下に示す。完全なコードはGitHubを参照していただきたい。

main1.py

#
# 制御点座標{bs[k][m]:k=0,3;m=0,1}と、
#   媒介変数{t[i]:i=0,N-1}について最適化
#
# N=データ点の数
#
# bs0: 制御点の初期値。ndarray。shape=(4,2)
# t0: データ点に対応する媒介変数の初期値。ndarray。shape=(N,)
# r0: データ点の座標。ndarray。shape=(N,2)
# rate: 学習係数
# nstep: 総ステップ（中断後に実行する場合もある）
# loop: 逐次回数
#
# 注) コード中の説明で、obj.shapeという表現は簡単のためであり、
# objがnp.ndarrayの場合は正しいが、objがtf.Tensorの場合には正しくない。
# tf.Tensorの場合にshapeを求めるには、tf.Tensor.get_shape()を使用する
#
#
def steps(bs0, t0, r0, rate, nstep, loop):
    # 新しいGraphを作成
    g = tf.Graph()

    # 作成したGraphをデフォルトにして、Operationを登録する
    with g.as_default():
        # [グラフの作成開始]
        cr0 = tf.constant(r0, tf.float32, ,name='r0')

        # 各データ点に対する媒介変数の値を最適化パラメータとする。t.shape=(N,)
        t = tf.Variable(t0, tf.float32, name='t')

        # 制御点を最適化パラメータとする。bs.shape = (4,2)
        bs = tf.Variable(bs0, tf.float32, name='bs')

        # 各制御点との積をとるための、tおよび(1-t)の冪。T.shape = (4, N)
        one = tf.constant(1., tf.float32, name='1')
        s = one - t
        T = tf.pack([s * s * s, 3 * s * s * t, 3 * s * t * t, t * t * t])

        # 各{t_i;i=0,n-1}に対して、補間曲線を計算する。r.shape = (N, 2)
        r = tf.matmul(T, bs, transpose_a=True)

        # 変数の初期化操作
        init = tf.initialize_all_variables()

        # 目的関数（Loss関数）の作成操作
        diff = tf.reduce_mean(tf.square(r - r0))

        # 最適化操作
        train = tf.train.GradientDescentOptimizer(rate).minimize(diff)

        # [*1] 結果出力のための挿入位置
        # [グラフの作成終了]
        g.finalize()

    # [*2]

    # Sessionを作成（明示的にGraphを渡す）
    with tf.Session(graph=g) as sess:
        # 初期化の実行
        sess.run(init)
        # [*3]
        print_result(nstep, sess, diff)

        for step in range(loop):
            # 最適化の実行
            sess.run(train)
            nstep = nstep + 1
            if nstep % 1000 == 0:
                # [*3]
                print_result(nstep, sess, diff)

        # Tensorの値を出力
        bs1, t1 = sess.run([bs, t])
    return bs1, t1, nstep

コードの説明

step()関数の引数については、コード中のコメント行で説明している。関数内の流れは以下のようになる。

Graphを明示的に作成する
作成したGraphをデフォルトグラフとし、必要なOperationを登録する
- 定数を登録する
- 変数を登録する
- 演算を登録する
- 最適化操作を登録する
作成したGraphに対して、Sessionを開く
開いたSessionの中で、最適化等の各Operationを実行する

このうち、2.の登録順については、前方参照を守る限り、どの順番でも良い。また、nameキーワードを与えている場合があるが、これはデータフローグラフの自動作成のためである。「# [*1]」のような表現は、後でコードを付加（あるいは変更）するためのアンカーである。

ここで登場する各クラスと関数については、結果の議論の後に説明する。

結果

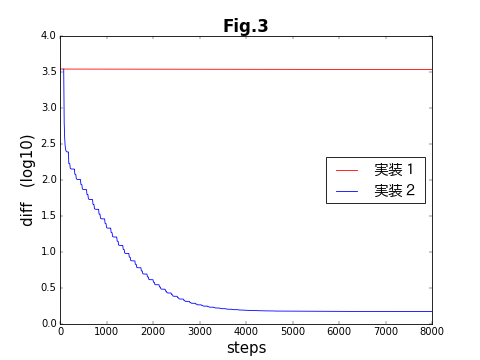
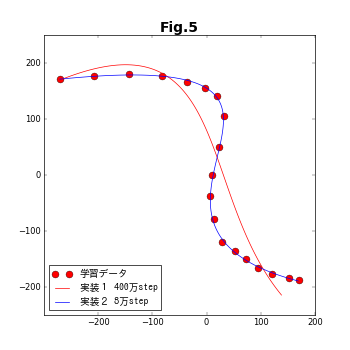
制御点と媒介変数の列を、両方共に最適化パラメータとした、今回のコードはうまく結果を出せない。下の図は、この節の方法（実装１）と次の記事（その２）で紹介する方法（実装２）の収束具合を比較したものである。結果があまにも違い過ぎるため、ひとつの図に収まるように、縦軸を対数表示している。次の記事で扱う実装２では5000ステップほどで収束しているのに対し、実装１では初期状態とほとんど変化していない。

その鍵となるのは、最適化アルゴリズム（tf.train.Optimizer）である。ここでは、最適化アルゴリズムとして最急降下法を用いている。最急降下法は、最適化パラメータが構成する多次元空間で、目的関数の勾配（接戦ベクトル）が最も急勾配になる方向を辿って行くという、直感的に分かりやすい方法である。ところが、数値計算をやったことがある方々は良くご存知だと思うが、この方法には欠点が多い。それでも、Deep Learningで最急降下法が用いられていることが多いのは、取扱いが易しいからだろう（「TensorFlowのOptimizerを比較する（ベジェ曲線編）」の記事の中で、TensorFlowで与えられている各種のOptimizerの性能を比較する）。

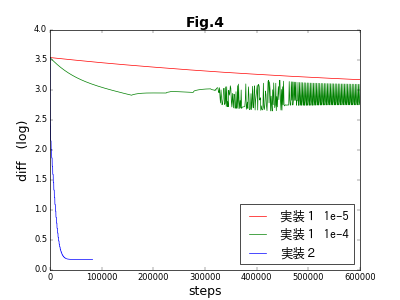
TensorFlowでの実装は、GradientDescentOptimizer()と言う長い名前のクラスで、学習係数（learning_rate）と呼ぶ唯ひとつの引数を取る。この係数は、目的関数の最適化パラメータに対する偏微分値を用いて、次のステップにおける最適化パラメータの予測値を導出する際に使用する。係数が大きいほど予測値が大胆になるが、大きすぎると結果が発散したり振動してしまう。逆に小さいと最適化されるまでの時間が長くなる。Fig.3では、learning_rate=0.00001を使用していたのだが、learning_rate=0.0001では、下図のように振動が起こる。さらに、learning_rateの値を大きくすると、完全に発散してしまう。

下図のうち赤線は、learning_rate=0.00001で400万ステップの最適化を行った結果である。残念ながら、全く補間の役割は果たしていない。実装１は失敗である。

失敗（最適化が収束しない）の原因

学習係数はたいへん微妙な因子である。種類が異なった最適化パラメータが複数ある場合、それぞれに適切な学習係数の値はみな違っている。実装２の結果を先取りして判断すると、$\{\boldsymbol{b}_k\}$と$\{t_i\}$に対する学習係数は、両者の間で5万倍も異なっていたのである。これでは、うまく行くはずがない。

これを踏まえて、実装２では、2種類のパラメータに対して別々の最適化操作を行い、それを交互に繰り返すことにより、この問題を克服する（図3で、実装２の結果が階段状になっているのは、別々の最適化が交互に行われているためである）。なお、記事が長くなるため、実装２は別の記事（その２）にする。

クラスと関数

結果がうまく行かなかったとは言え、上記のコードは完全に動作する。そこで、ここで使用しているTensorFlowのクラスと関数を、簡単に説明しておく。なお、簡略化のために、以下のaliasを行っている。

import tensorflow as tf

tf.Graph

TensorFlowの多くのコードでは、以下に示すようなGraphオブジェクトを明示的に使用する部分が、おもてに現れない。ところが、このGraphというオブジェクトは、TensorFlowの概念の基本となるオブジェクトなのである。その証拠に、TensorFlowのAPIドキュメントの最初に登場するクラスがtf.Graphである（以下、tf.Operation、tf.Tensorと続く）。

g = Graph()
with g.as_default():
    (グラフの作成=各種Operationを登録する)
    g.finalize()

ここでは、上のような形式でGraphの作成を行う。通常の計算ではデフォルトのGraphが設定されているので、Graphを一つしか使わない場合には、このように形式的に組む必要はない。しかし、ひとつには以降の説明のため、もうひとつは、実装２でGraphを２種類使用する必要があるために、ここでは明示的にGraphを使用する。

TensorFlowのプログラムは、形式にこだわらずに組んでも動作するという、良い意味での柔軟性がある。しかし、その柔軟性が逆にプログラムを分かりにくくしている。本来なら「with g.as_default()」と「g.finalize()」の間で明確に区切られるべき箇所が、露に見えないのである。ここでは、演算を行っているように見える行が、実際には、Graphオブジェクトへの、演算の登録であることが見えにくいのである。プロのプログラマの人たちには、形式にこだわることを是非、お勧めしたい。

tf.Graph.finalize()

finalize()という関数に初めて出会ったという方もいるのではないだろうか。この関数がなくても、ほとんどのプログラムが動作するという意味では、極めて形式的な存在である。しかし、プログラムの範囲を明確に示すには、私は好ましいと思う。finalize()は「これ以降Graphへの演算を登録することはできない」という意味である。これまではGraphが書き込み可能であったのが、これ以降はリードオンリーになるという意味である（「with g.as_default()」は、デフォルトグラフの範囲を示すだけで、Graphを閉じることはしない）。

g = Graph()
with g.as_default():
    ...
    g.finalize()
    diff2 = diff * 2.

従って、上のようなコードは、下のようにRuntimeErrorを引き起こす。

raise RuntimeError("Graph is finalized and cannot be modified.")

tf.Operation

TensorFlowの演算が通常の演算と決定的に異なっているのは、Operationがオブジェクトであり、実際の演算を行うわけではないところにある。Operationは、データフローグラフ（その実装がGraph）のノードであり、opと表記される。一連の計算の中における一つの操作（四則演算、関数操作...）がOperationである。Operationは入力と出力を持ち、出力は必ず、Tensorである。入力の多くもTensorである（numpy.ndarrayやリストであることもある）。このため、OperationとTensorは切り離せない。

tf.Tensor

TensorFlowによるデータの流れの中でデータを保持するオブジェクトがTensorである。Tensorのデータ構造は、名前のごとくテンソルと同じ構造をしている。通常のテンソルであるならば、例えば、[[2,3,4],[4,5,6]]は2x3の2階テンソルであり、[[[1,2],[3,4]]]は1x2x2の3階テンソルである。Tensorにはshapeという概念があり、前者のshapeは(2,3)、後者のshapeは(1,2,2)となる。

TensorFlowの演算

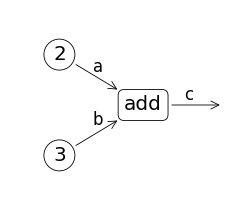
例えば下のコード中で、「c = a + b」を考えてみる。ここで、中心となるOperationは「+」である。その入力がaとbという２つのTensorであり、出力がcというTensorである。

a = tf.constant(2)
b = tf.constant(3)
c = a + b

ここで、「c = a + b」が実行された結果は、どうなるのだろうか？

この段階では演算がなされるわけではない。実行されるのは「aとbを加算して結果をcに保持せよ」といういわば「プログラム」がセットされるのである。このプログラムにあたるのがGraphである。その意味では、上のコードはプログラム（Graph）を作るプログラムと言える。このため、「c = a + b」を実行した直後には、Tensorは数値と結び付けられていない。

データフローグラフ

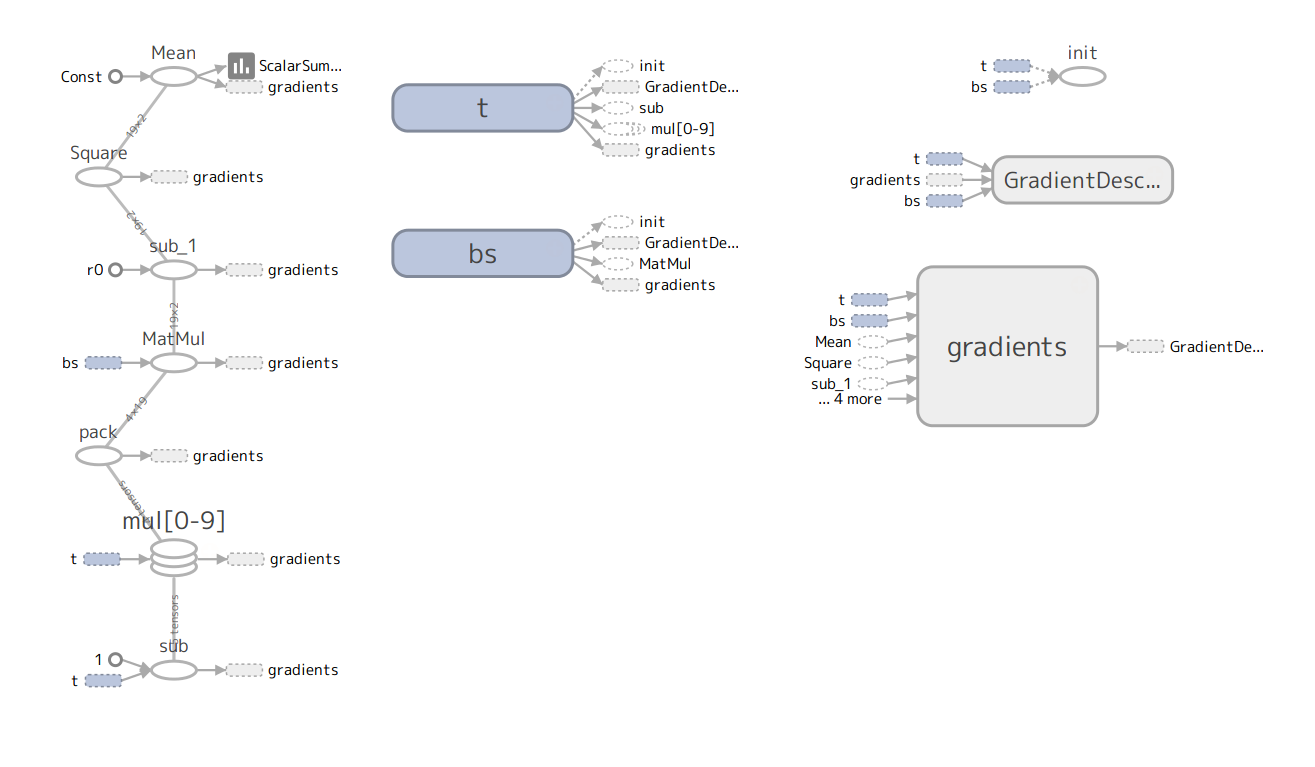
下図は、上のコードに対応するデータフローグラフである。データフローグラフの全体は、Graphに対応する。四角や丸で囲まれたのが演算を表現するopノードであり、Operationに対応する。矢印は流れるデータを表現するエッジであり、Tensorに対応する。すなわち、データはTensorオブジェクトとして流れる（Flow）のである。これが、TensorFlowという名前の由来であろう。

TensorFlowでは、データフローグラフを出力する機構が備わっている。この記事の最後に、それを使う方法を説明する。

Tensorの値

Tensorの値はそのインスタンスを引数にして、Sessionのrunコマンドを実行することで得られる。得られた値は、通常ならnumpy.ndarray型であり、そのshapeは元のTensorオブジェクトのshapeと同じである。例えば、関数tf.constant()で作成される"定数のTensor"の値は次のように出力される。

a = tf.constant([1., 3., 2.])
with tf.Session() as sess:
    print(sess.run(a))

出力結果


[ 1.  3.  2.]

2段階の実行プロセス

このように、TensorFlowの計算は2段階になっている。

Tensorに対するOperationを登録する（グラフを作成する）
Sessionを開いて、その中でグラフ（の一部）を実行する

このような2段階でTensorFlowが実行されるのは、次の理由がある。

Pythonとライブラリのやり取りにかかるオーバーヘッドを減らす
GPU等を使った複雑な並列化処理を隠蔽する

このため、実際には膨大な計算が行われているにも関わらず、そのために組まれるPythonプログラムは、有り難いことにたいへんシンプルになる。

各種Operation

四則演算

Tensor同士で四則演算を行った結果は、Tensorである。また、次に説明するVariableとTensorで演算を行った結果も、Tensorである。

x、yをTensorとしたとき、x*yは、それぞれの要素ごとの積を要素とするTensorである。一般的には、四則演算が成立するためには、xとyのshapeが同じでなければならない。ただし、shapeが一致しなくても演算が成立する場合もあるので、注意が必要である（broadcasting）。

x = tf.constant([2., 3., 5.])
y = tf.constant([3., -1., 2.])
q = x * y
with tf.Session() as sess:
    print(sess.run(q))

出力結果


[  6.  -3.  10.]

演算子に対応する関数が存在するので、「c = a + b」の代わりに、「c = tf.add(a,b)」のようにすることも出来る。関数型の方にはnameキーワードを追加することが出来るが、コードの見やすさとのバーターである。

算術関数

tf.sqrt()のような算術関数をTensorに作用させた結果も、各要素に別々にその関数を作用させた結果になる。

x = tf.constant([9., 16., 25.])
q = tf.sqrt(x)
with tf.Session() as sess:
    print(sess.run(q))

出力結果


[ 3.  4.  5.]

縮約系関数

reduce_XXX()という名前がついた関数は、要素を縮約する。第2引数を指定しなければ、結果は全次元について縮約した結果としてのスカラーになる。第2引数が指定された場合、それは縮約を行う次元を指定する。このうち、reduce_mean()は、関係する要素の平均を取る。

x = tf.constant([[1., 2., 3.], [3., 4., 5.]])
q = tf.reduce_mean(x)
q0 = tf.reduce_mean(x,0)
q1 = tf.reduce_mean(x,1)
with tf.Session() as sess:
    print(sess.run([q, q0, q1]))

出力結果


[3.0, array([ 2.,  3.,  4.], dtype=float32), array([ 2.,  4.], dtype=float32)]

tf.pack()

いま、s、tをshape=(m,)のTensorとしたとき、[s, t]はリストになる。これにtf.pack()を作用させることにより、shape=(2,m)のTensorを作成することができる。

x = tf.constant([1., 2., 3.])
y = tf.constant([3., 4., 5.])
q = tf.pack([x, y])
with tf.Session() as sess:
    print(sess.run(q))

出力結果


[[ 1.  2.  3.]
 [ 3.  4.  5.]]

tf.matmul()

matmul(x,y)は、Tensorを行列のように乗算するための関数である。xとyを2階のTensorとするとき、xの2次元目とyの1次元目のサイズが一致していなければならない。上にあげたプログラムのように、xを転置する必要がある場合は、キーワード引数を「transpose_a=True」のように指定する。ここで「_a」を「_b」に変えると、第2引数を転置するという意味になる。

x = tf.constant([[1., 2., 3.], [3., 4., 5.]])
y = tf.constant([[1., 2.], [3., 4.], [5., 6.]])
q = tf.matmul(x, y)
print('x.shape=', x.get_shape(), 'y.shape=', y.get_shape(),
    'q.shape=', q.get_shape())
with tf.Session() as sess:
    print(sess.run(q))

出力結果


(2, 3) (3, 2) (2, 2)
[[ 22.  28.]
 [ 40.  52.]]

tf.Variable

最適化の際のパラメータを定めるオブジェクトが、Variableである。Variableに対する各種の演算は、基本的にTensorと同じ性質を持つ。Variableに何らかの演算を施すと、結果はTensorになる。

Optimizerに渡す目的関数の導出過程に含まれるVariableは、この目的関数に対する最適化パラメータである。とても簡単な次のコードを見ていただければ、Variableの役割が分かるだろう。ここでは、xが最適化パラメータ、yが目的関数である。

main2.py

rate = 0.4
loop = 10
x = tf.Variable(0.)
y = (x  - 2.) * (x - 2.) + 1.
init = tf.initialize_all_variables()
optimize = tf.train.GradientDescentOptimizer(rate).minimize(y)

with tf.Session() as sess:
    sess.run(init)
    x0, y0 = sess.run([x,y])
    print(0, ') x =', x0, ', y =', y0)
    for step in range(loop):
        sess.run(optimize)
        x0, y0 = sess.run([x,y])
        print(step+1, ') x =', x0, ', y =', y0)

実行結果


0 ) x = 0.0 , y = 5.0
1 ) x = 1.6 , y = 1.16
2 ) x = 1.92 , y = 1.0064
3 ) x = 1.984 , y = 1.00026
4 ) x = 1.9968 , y = 1.00001
5 ) x = 1.99936 , y = 1.0
6 ) x = 1.99987 , y = 1.0
7 ) x = 1.99997 , y = 1.0
8 ) x = 1.99999 , y = 1.0
9 ) x = 2.0 , y = 1.0
10 ) x = 2.0 , y = 1.0

numpy.ndarray

この関数の仮引数のうち、最初の３つはNumPyライブラリのndarrayである。TensorFlowで扱うtf.Variable、tf.Tensorなどのクラスは、Python本体のリストより、ndarrayとの馴染が良いため、データの受け渡しにはndarrayを使うのが便利である。

結果の可視化

tf.train.SummaryWriter

TensorFlowの実行結果を出力するための機構である。

指定されたディレクトリの中に

events.out.tfevents.TIMESTAMP.HOST

のような名前の「eventファイル」として書き出す。ここでTEIMESTAMPは開始時刻、HOSTはホスト名である。ファイル名は指定できないようなので、違ったプログラムを実行する必要がある場合にはディレクトリを変更した方が良い。参照１のプログラム例では、diffの値をprintしているが、実行の速度を必要とする場合は避けた方が良い。SummaryWirterは非同期なので実行速度に影響しない。

実装１のプログラム中のアンカー部分に、以下のように挿入あるいは変更するだけで、SummaryWriterの実装ができる（インデントは、アンカーの場所に合せて適切に取って頂きたい）。

# 挿入場所に合わせて、インデントしてください
# [*1]
tf.scalar_summary('diff', diff)
summary_op = tf.merge_all_summaries()

# [*2]
summary_writer = tf.train.SummaryWriter('data', graph=g)

# 2箇所ある。アンカー以下の1行を削除、2行を挿入
# [*3]
summary_str = sess.run(summary_op)
summary_writer.add_summary(summary_str, nstep)

ここで、記録しているのは

ステップごとのdiffの値
データフローグラフ

の２種類である。SummaryWriterのコンストラクタでgraphキーワードを指定することにより、データフローグラフが作成できるところが、とても便利だ。コンストラクタを置く位置には注意が必要である。必ず、Operationの登録が済んだ後で行う必要がある。また、ここではGraphを明示的に作成しているので「graph=g」を指定しているが、明示的に作成しない場合には、Sessionを開いた後に実行し、「graph=sess.graph」を指定する必要がある。なお、graph_defキーワードを指定しているプログラム例も見受けられるが、これはDEPRECATEDなので、避けた方が良い。

tf.scalar_summary()

値を保存するTensor（またはVariable）と、それにつけるラベルをsummaryとして登録する。Tensorがスカラー（shape=()）である必要はないが、ラベルのshapeと値のshapeを合わせておく必要がある。例えば、上記プログラム中（main1.py）のbsはshape=(4,2)のVariableだが、この値をsummaryにする場合は、以下のようにラベルも4x2にしなければならない。

tf.scalar_summary([['bs0_x', 'bs0_y'], ['bs1_x','bs1_y'],
    ['bs2_x', 'bs2_y'], ['bs3_x', 'bs3_y']], bs)

tf.merge_all_summaries()

この関数の実行までに登録された全てのsummaryをOperationとして登録する。従って、Graphが閉じていないうちに実行しなければならない。また、この関数の戻り値として得られたTensorは、他のTensorと同様、Session内でrun()を行い、summaryの値を得る必要がある。summaryの値は、他のTensorやVariableの値とは異なり、バイト列（bytes）である。このバイト列は、以下のadd_summary()に引数として送る。

tf.train.SummaryWriter.add_summary()

Session内で値にしたsummaryの結果を出力する。第2引数はグローバルステップである。各summaryの値は、グローバルステップを横軸に取ってプロットされる。

TensorBoard

得られたeventファイルを見るためのアプリケーションがTensorBoardである。以下のように実行する。

$ tensorboard --logdir=data

tensorboardは一種のWebサーバで、デフォルトでは「0.0.0.0:6006」のURLを持つので、ブラウザでアクセスすれば良い。0.0.0.0ではどこからのアクセスも許すので、セキュリティーの問題が生じる可能性がある。その場合には、「--host=localhost」をコマンドライン引数に付加すれば、「localhost:6006」でしかアクセスできない。ポート番号も「--port=XXX」で変更できる。

以下は、TensorBoardの出力から得られた、main1.pyに対するデータフローグラフである。

参照

変更履歴

2019-09-02: TensorFlowのドキュメントのリンクを変更した r0.10 -> r1.14
2019-01-03: 表式に番号を付加した。(1)式の表記を変更した
2018-12-19: コード中の変数名と一致させるため、パラメータの名前を変更した（$\boldsymbol{a}_k$ -> $\boldsymbol{b}_k$）