TensorFlowでニューラルネットワークを学習させることは、つまるところ、教師データに対して損失関数を最小化することである。これは最小二乗法による線形回帰の問題と、とてもよく似ている。そのため、この種の最適化問題はTensorFlowのフレームワークに慣れるための演習として良く用いられる。
前の記事では、広い意味での線形回帰として、3次の補間ベジェ曲線を求める問題を解いてみた。その過程では期待どおり、Graph、Tensor、Variableというような、TensorFlowの基本的オブジェクトの働きが、かなり明白になった。
ところが、ベジェ曲線を最適化するという当初の目的においては、最適化をうまく収束させることができなかった。その原因は、最適化のためのパラメータ(TensorFlowの用語で言えば、Variable)に、下に示す異なった2種類のバラメータを同時に使用したからである。1.はベジェ曲線の4個の制御点、2.はデータ点に対応する媒介変数(Nはデータ点の総数)である。
- $ \{\boldsymbol{b}_k:k=0,3\} $
- $ \{t_i:i=0,N-1\} $
この2種類のパラメータに対する適切な学習係数(learning_rate)が大きく異なっているため、learning_rateにどんな値を使っても、最適化プロセスが発散するか、振動するか、いつまでたっても収束しないということになってしまったのである。ここでは、これを回避するために、以下のような手順で実装を行う。
- 2種類の最適化パラメータのうち、1種類だけをパラメータとする(もうひとつは定数とする)、2種類の最適化を交互に利用する(実装2)
- 計算コストを軽減するために、GraphとSessionを流用する(実装3)
これを実装する過程で、GraphとSessionの意味がより明白になる。また、必要のためにtf.placeholder()を導入したことにより、その意義を確認することができた。
なお、ここでOptimizerとして用いているのは、GradientDescentOptimizerである。このOptimizerは最急降下法を用いたものであり、最も単純なOptimizerである。TensorFlowには、これ以外に各種の確率的勾配降下法を用いたOptimizerがあり、「TensorFlowのOptimizerを比較する(ベジェ曲線編)」の記事の中で、ここで用いた主題(ベジェ曲線の最適化)を使って、各種のOptimizerの性能を比較検討する。
実装2
そこで、2種類のパラメータについて、交互に最適化する。
| $\{\boldsymbol{b}_k\}$ | $\{t_i\}$ | 学習係数 | ||
|---|---|---|---|---|
| Phase 1 | 制御点に対する最適化 | Variable | 定数Tensor | 5.0 |
| Phase 2 | 媒介変数に対する最適化 | 定数Tensor | Variable | 0.00001 |
ところが、この場合には問題がある。それは、2種類の最適化でデータフローグラフが異なるのである。通常は1種類のグラフしかないため意識することはないのだが、Tensorに対する演算はデフォルトのグラフに登録される。そのため、2種類の最適化が同じグラフに登録されてしまい、互いに矛盾が起きてしまう。
これを逃れるためには、別々のGraphオブジェクトを明示的に作成しなければならない。その1では、既に、この方式(明示的なGraphの作成)を導入していたのだが、改めて以下に示す。
g = Graph()
with g.as_default():
グラフの作成
g.finalize()
with Session(graph=g) as sess:
sess.run(グラフに登録したop)
g.as_default()は、gをデフォルトグラフとして設定し、それ以降に行われたTensorに対する演算はgに登録される。ここで、Sessionに対するwith文は、以下のように「入れ子にする必要がない」ことに注意して頂きたい。Sessionを開始する前に、グラフの作成は終わっているからである。
# 入れ子にする必要はない
g = Graph()
with g.as_default():
グラフの作成
g.finalize()
with Session(graph=g) as sess:
sess.run(グラフに登録したop)
Phase1:制御点に対する最適化
完全なコードは、GitHubを参照していただきたい。
#
# ベジェ制御点{bs[k]:k=0,3}についての最適化
#
# bs0: 制御点の初期値。ndarray。shape=(4,2)
# t0: データ点に対応する媒介変数の初期値。ndarray。shape=(n,)
# r0: データ点の座標。ndarray。shape=(n,2)
# rate: 学習係数
# nc: 総ステップ数
# loop: 逐次回数
#
def phase1(bs0, t0, r0, rate, nstep, loop):
g = tf.Graph()
with g.as_default():
# [グラフの作成開始]
# 入力となるN個の教師データ。shape = (N,)
t = tf.constant(t0, tf.float32)
# T.shape = (N, 4)
# ちょっと手抜きをした記述
s = 1 - t
T = tf.pack([s * s * s, 3 * s * s * t, 3 * s * t * t, t * t * t])
# 4個の制御点の座標。最適化パラメータ。bs.shape = (4,2)
bs = tf.Variable(bs0, tf.float32)
# 各データ点に対応する補間曲線上の点。r.shape = (N,2)
r = tf.matmul(T, bs, transpose_a=True)
# tf.Variableの初期化を行うOP
init = tf.initialize_all_variables()
# 目的関数
# 手抜きをしてr0を直接、演算に投入している
diff = tf.reduce_mean(tf.square(r - r0))
# トレーニング操作(最適化)
train = tf.train.GradientDescentOptimizer(rate).minimize(diff)
# [グラフの作成終了]
g.finalize()
with tf.Session(graph=g) as sess:
sess.run(init)
print_result('P1', nstep, sess, diff)
for step in range(loop):
sess.run(train)
nstep = nstep + 1
if (step + 1) % 10 == 0:
print_result('P1', nstep, sess, diff)
bs1 = sess.run(bs)
return bs1, t0, nstep
これは、制御点だけを最適化する関数である。その1と比べると、データフローグラフの出力を意識していないためnameキーワードを設定していないこと、定数データをtf.constant()を使用せずに直接、演算へ代入しているなど、いくつかの手抜きをしている。しかし、それらは本質的なことではなく、重要な変更点は以下だけである。
# main1.py (nameキーワードはグラフ出力のためで、重要な変更ではない)
t = tf.Variable(t0, tf.float32, name='t')
# main3.py/phase1()
t = tf.constant(t0, tf.float32)
前者ではtがVariableオブジェクトであるのに対し、後者ではtが定数Tensorであることだけが異なっている。これだけの変更にもかかわらず、学習係数(rate)は、5.0でも収束するのである。
Phase2:媒介変数に対する最適化
#
# 各データ点に対応する媒介変数値{t[i]:i=0,N-1}についての最適化
# 各引数は、phase1()に同じ
#
def phase2(bs1, t1, r0, rate, nstep, loop):
g = tf.Graph()
with g.as_default():
# t1の両端を切り取る st1.shape = (N-2,)
st1 = t1[1:len(t1) - 1]
# t[0]を0に固定するための定数
fti = tf.constant([0.])
# t[N-1]を1に固定するための定数
ftf = tf.constant([1.])
# 両端を切り取ったt1を初期値として、1階の変数Tensorを作成する
st = tf.Variable(st1)
# stの両端に定数を加えて、1階のTensorを作成する
t = tf.concat(0, [fti, st, ftf])
# 入力に相当する1個で、4x2サイズの教師データ。bs.shape = (4,2)
bs = tf.constant(bs1)
# T.shape = (4, N)
s = 1 - t
T = tf.pack([s * s * s, 3 * s * s * t, 3 * s * t * t, t * t * t])
# 各{t_i;i=0,n-1}に対して、補間曲線を計算する。r.shape = (N, 2)
r = tf.matmul(T, bs, transpose_a=True)
init = tf.initialize_all_variables()
diff = tf.reduce_mean(tf.square(r - r0))
train = tf.train.GradientDescentOptimizer(rate).minimize(diff)
g.finalize()
with tf.Session(graph=g) as sess:
sess.run(init)
print_result('P2', nstep, sess, diff)
for step in range(loop):
sess.run(train)
nstep = nstep + 1
if (step + 1) % 10 == 0:
print_result('P2', nstep, sess, diff)
t2 = sess.run(t)
return bs1, t2, nstep
phase2()の方は、phase1()に比べて、分かりにくくなっている。その原因は、
t_0=0, t_{N-1}=1
という束縛条件を入れているからである。それは、$\{t_i\}$に曖昧さがあるからである。$\{t_i\}$に定数を加えたり、定数倍しても、$\{\boldsymbol{b}_k\}$で調整すれば、ほぼ同じ補間曲線が得られる。この曖昧さを解消するために、両端を固定するのである。
数値的な最適化を行う際に、束縛条件を導入するのは、かなり難しい。理論上ではラグランジェの未定係数法を使うのだが、未定係数法では、目的関数が最大値または最小値を持つことが保証されないため(鞍部点であることが多い)、数値計算では発散してしまうのである。そこでコード中に、直接、束縛条件を入れ込むことにする。ところが、tが定数の列である場合には簡単に実現できるのに対し、tがVariableの場合は、束縛条件のついた両端を、あらかじめVariableから除いておかなければならない。そのため、main1.pyと比較すると以下のように、手順が増えている。
# main1.py (nameキーワードはグラフ出力のためで、重要な変更ではない)
t = tf.Variable(t0, tf.float32, name='t')
bs = tf.Variable(bs0, tf.float32, name='bs')
# main3.py/phase2()
st1 = t1[1:len(t1) - 1]
fti = tf.constant([0.])
ftf = tf.constant([1.])
st = tf.Variable(st1)
t = tf.concat(0, [fti, st, ftf])
bs = tf.constant(bs1)
こうして、phase2()では、$\{t_i:i=1,N-2\}$だけを最適化パラメータとすることができたのだが、その収束のためには、学習定数が0.00001という小さい値でなければならないことが判明したのである。
交互に最適化
こうして、得られた2種類の最適化関数を、以下のように交互に使用する。
def do_cycle(nd, r0):
bs2 = get_initial_control_points(r0)
t2 = get_initial_ts(r0, bs2)
nstep = 0
for id in range(nd):
bs1, t1, nstep = phase1(bs2, t2, r0, 5.0, nstep, 100)
bs2, t2, nstep = phase2(bs1, t1, r0, 1e-5, nstep, 30)
return bs2, t2, nstep
$\{t_i\}$に対する最適化では、学習曲線が0.00001という小さい値である反面、30ステップほどで、ある程度収束してしまう。2種類の最適化を1サイクルとして、これを繰り返すわけである。
結果
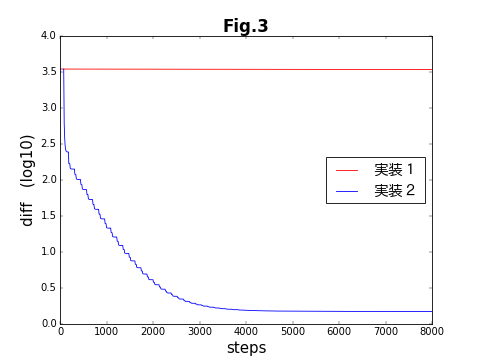
前の記事でも示した、目的関数が収束する様子を示した図を、再び示す。横軸は、両方の最適化を合わせた全ステップ数である。5000ステップ程度で、ほぼ収束している。これは、ほぼ50サイクルに相当する。改めて最適化を分解する前(実装1)と比べると、実装2が成功したことが分かる。グラフが階段状になっているのは、交互に2種類の最適化が繰り返されているからである。
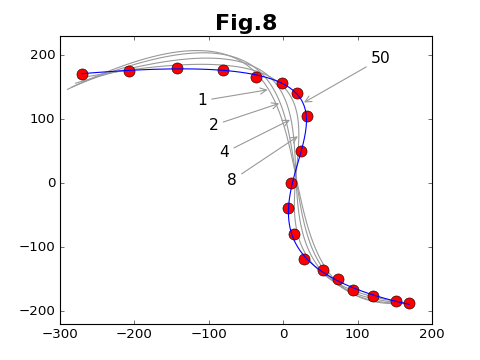
収束の様子を、データ点と各段階での補間曲線と比較したのが下図である。図中の数字は、サイクル数である。サイクル数の130倍がステップ数に相当する。
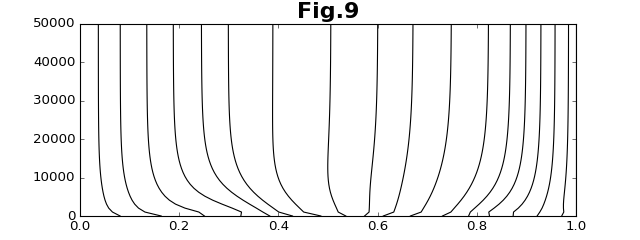
このとき、各データ点に対応する媒介変数$\{t_i:i=1,N-2\}$の値は、次のように変化する。縦軸がステップ数である。なお、両端のデータ点の媒介変数は、それぞれ、$t_0=0$と$t_{N-1}=1$に固定している。
ところで、実際にこのコードを実行してみると、1サイクル毎に実行が止まってしまう瞬間が起きる。この原因は、phase1()/phase2()共に、関数の内部で1回ごとにGraphとSessionを生成しているためである。Graphオブジェクトインスタンスの生成とSessionオブジェクトインスタンスの生成は、共にコストが大きい操作である。この問題は、実装3で解決する。
実装3
GraphならびにSessionのインスタンスを維持し、それぞれのサイクルで共用すれば、コストの大きいインスタンスの生成という操作を逃れることができる。だが、TesnforFlowのサイトを見た限りでは、このようなことが可能かどうか良く分からない。まずは、試みてみることにする。
GraphPhase1クラス
main3.pyのphase1()関数に対応するクラスを実装する。phase2()に対応するクラスも必要だから、共通の部分は基底クラスGraphPhaseで実装する。ここにはコンストラクタだけを表示しているが、これが鍵である。コンストラクタの中では、最初にGraphを生成し、そのインスタンスを用いてSessionを生成している。
GraphPhase1のコンストラクタは、ただ一つの引数rateを取る。rateは学習係数である。rateは、Optimizerのminimize()メソッドに与える引数であるから、GraphへOperationを登録するために必要である。クラスでの実装の唯一の欠点は、「self.」を付ける必要のためにコードが煩わしくなる点である。
class GraphPhase:
def __init__(self):
self.g = tf.Graph()
self.sess = tf.Session(graph=self.g)
self.writer = None
(一部省略)
class GraphPhase1(GraphPhase):
def __init__(self, rate=None):
GraphPhase.__init__(self)
self.rate = rate
with self.g.as_default():
# 最適化パラメータとしての制御点を(形式的に)初期化するため
self.bs0 = tf.placeholder(tf.float32, shape=(4, 2), name='bs0')
# 入力となるN個の教師データ。shape = (N,)GraphとSession
self.t = tf.placeholder(tf.float32, shape=(None,), name='t')
# ラベルとなるN個の教師データ。shape = (N,2)
self.r0 = tf.placeholder(tf.float32, shape=(None, 2), name='r0')
# T.shape = (4,N)GraphとSession
self.s = 1 - self.tGraphとSession
self.T = tf.pack(
[self.s * self.s * self.s, 3 * self.s * self.s * self.t,
3 * self.s * self.t * self.t, self.t * self.t * self.t])
# 4個の制御点の座標。最適化パラメータ。bs.sGraphとSessionhape = (4,2)
self.bs = tf.Variable(self.bs0, tf.float32, name='bs')
# 各データ点に対応する補間曲線上の点。r.shape = (N,2)
self.r = tf.matmul(self.T, self.bs, transpose_a=True)
# tf.Variableの初期化を行うOPGraphとSession
self.init = tf.initialize_all_variables()
if self.rate is not None:
# 目的関数
self.diff = tf.reduce_mean(tf.square(self.r - self.r0))
# トレーニング操作(最適化)
self.train = tf.train.GradientDescentOptimizer(self.rate)\
.minimize(self.diff)
tf.scalar_summary('diff', self.diff)
self.summary = tf.merge_all_summaries()
else:
self.diff = None
self.summary = None
self.g.finalize()
def execute(self, bs0, t0, r0, nc, loop):`
if self.rate is None:
return None, None, None
# 最適化のために、placeholderに値を代入するための辞書
feed_dict = {self.t: t0, self.r0: r0}
# 初期化。初期化のためのplaceholderにbs0をセット
self.sess.run(self.init, feed_dict={self.bs0: bs0})
self.print_result('P1', nc, self.sess,
self.diff, self.summary, feed_dict)
for step in range(loop):
self.sess.run(self.train, feed_dict=feed_dict)
nc = nc + 1
if (step + 1) % 100 == 0:
self.print_result('P1', nc, self.sess,
self.diff, self.summary, feed_dict)
bs1 = self.sess.run(self.bs)
return bs1, t0, nc
def get_points(self, bs0, t0):
self.sess.run(self.init, feed_dict={self.bs0: bs0})
r1 = self.sess.run(self.r, feed_dict={self.t: t0})
return r1
tf.placeholder()
ここで初めて、tf.placeholder()が登場した。注意が必要なことは、placeholder()は、クラスではなく関数だということである。戻り値は、Tensorオブジェクトである。その意味では、tf.constant()と良く似ている。constant()もTensorオブジェクトを戻す関数である。両者の違いは、constant()は値の定まった定数Tensorを戻すのに対し、placeholder()が戻すTensorオブジェクトでは、関数を実行した時点では内容が決まっておらず、型とshapeが決まっているだけだというところにある。
placeholder()を使用するメリットは、GraphとSessionの流用と関係している。GraphPhase1のコンストラクタで、placeholder()で生成しているTensorは、
- self.bs0
- self.t
- self.r0
の3種類である。このうち、self.bs0とselft.tは、それぞれのフェーズにおける最適化パラメータに対応しており、各サイクルごとに変化する。そのため、コンストラクタの実行時には値が定まっていないので、constant()を使うことが出来ない。実装2でそれができたのは、1サイクル毎にGraphインスタンスを作成していたからである。ここでは、placeholder()を使用するのが必然なのである。
なお、self.r0は、データ点に対応するものなので、コンストラクタにデータ点列を送っておけば、constant()を利用できる。ここでは、TensorFlowのExampleプログラム(MNIST)と形式的な類似を強調するために、敢えてplaceholder()を使用している。
各サイクルでの最適化
各サイクルでは、
execute(self, bs0, t0, r0, nc, loop)
を実行する。ここで、制御点列bs0と媒介変数列t0は、各サイクルで異なっている。placeholder()で作成したTensorオブジェクトは、Session.run()での実行時に、割り当てるべき値を、feed_dictキーワードを使って割り当てる必要である。ここでは3個の未定Tensorオブジェクトがあるが、全部を同時に割り当てる必要はない。例えば、初期化(self.init)の際に必要なのは、self.bs0だけである。逆に、self.diffを使う場合には、self.t0とself.r0が必要になる。
ここでは、GraphPhase2クラスは省略するが、完全なコードは、GitHubを参照していただきたい。2つのクラスは以下のように呼び出し、実行する。クラスインスタンスを流用していることがお分かりだろう。グラフとSessionの作成は、それぞれのクラスで一回づつ行われるだけである。
def do_cycle(nd, r0):
bs2 = fitter4.get_initial_control_points(r0)
t2 = fitter4.get_initial_ts(r0, bs2)
gr1 = fitter4.GraphPhase1(5.0)
gr2 = fitter4.GraphPhase2(1e-5, len(t2))
writer = fitter4.create_summary_writer('data/main4')
gr1.set_summary_writer(writer)
gr2.set_summary_writer(writer)
writer.add_graph(gr1.get_graph())
dk = fitter4.DataKeeper()
nc = 0
dk.append(bs2, t2, nc)
for id in range(nd):
bs1, t1, nc = gr1.execute(bs2, t2, r0, nc, 100)
bs2, t2, nc = gr2.execute(bs1, t1, r0, nc, 30)
dk.append(bs2, t2, nc)
return dk
return dk
結果
この結果、実行時間は、以下のようになる。
| 実行時間 | |
|---|---|
| GraphとSessionを、毎回生成する | 98秒 |
| Sessionだけを、毎回生成する | 52秒 |
| 両方とも流用する | 29秒 |
placeholder()の効用
上記、GraphPhase1クラスに、get_points()メソッドがあることに注目して頂きたい。これが、placeholder()で作成した未定Tensorの効用である。
self.t = tf.placeholder(tf.float32, shape=(None,), name='t')
placeholder()で、self.tを作成した際、上のように、サイズが不明の1階テンソルとして作成していたことを思い出していただきたい。tはデータ点列に対応する媒介変数列であるから、今までは(実装1や実装2)、データ点列の点の数と同じサイズだった。しかし、placeholder()で作成したTensorでは、Noneを指定することにより、次元のひとつ(複数の次元でNoneを指定できるかどうかは不明)のサイズを未定にすることができる。
x = tf.placeholder(tf.float32,[None,784])
例えば、TensorFlowサイトのMNISTのExample(TutorialはTensorFlowのサイト、コードはGitHub)では、上のように、2次元のうち最初の次元を未定にしている。ここで、xというTensorはデータ画像を格納するものであり、2次元目の784は28x28サイズの画像のピクセルを1列に並び替えたものであり、1次元目は画像を識別する。従って、xには複数の画像を同時に格納できる。
これにより、ニューラルネットワークの学習時には、並列化のレベルをあげるために多くの画像を同時に投入し(Exampleプログラムでは、100画像を同時に処理している)、実際に利用する際には1個づつ投入することができる。これが、placeholder()の効用である。
上にあげた図8は、GraphPhase1のコンストラクタと、get_points()メソッドを使って描いている。
gr1 = fitter4.GraphPhase1()
data = np.load('../data/m-cap.2.main4.npz')
bss = data['bss']
t = np.linspace(0., 1., 101)
r = gr1.get_points(bss[-1], t)
ax.plot(r[:,0], r[:,1], color='blue')
関連する部分だけを取り出すと、上のようになる。ここで、m-cap.2.main4.npzは、main4.pyの実行結果を格納したファイルである。ここでは、tのサイズは101個であるが、placeholder()の自由度のおかげで、最適化に使用したクラスを流用して、簡単にグラフを作成できる。
前の記事も含めて、挿入した図はMatplotlibを使って作成している。そのコードも、同じGitHubに置いてあるので、作図の参考になるかも知れない。
参照
変更履歴
- 2019-09-02: TensorFlowサイトへのリンクを変更した。低水準APIのチュートリアルが参照できなくなっている
- 2018-12-19: コード中の変数名と一致させるため、パラメータの名前を変更した($\boldsymbol{a}_k$ -> $\boldsymbol{b}_k$)