こちら練習問題になっていますが、元ネタは2015年に実際に行われていたこちらのコンペのようです。
このモデルのRMSEは6.69380で、本投稿時6位相当でした。
データ分析の基本的な流れは網羅できていると思いますので、参考になれば幸いです。
目次
以下の順に沿って解説していきます。
- データの可視化
- トレンド抽出
- 特徴量エンジニアリング
- 特徴選択
- モデル作成
- テストデータの前処理と予測
1. データの可視化
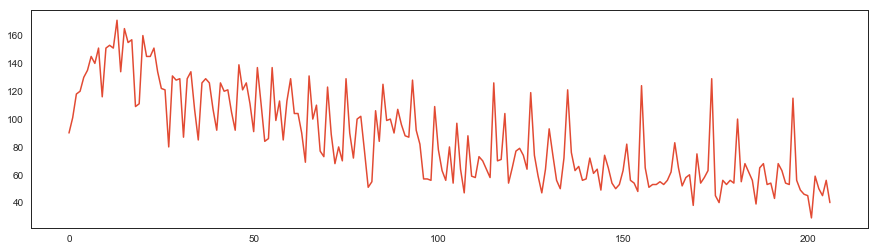
まず目的変数である販売数の変動を可視化します。
train = pd.read_csv('../train.csv')
test = pd.read_csv('../test.csv')
train['y'].plot
販売数をみて気になったこと:
- チュートリアルにもある通り、初めの数十レコードは傾向が違う。ので、丸っと落としました
- 明らかに右下がりのトレンドがあります。方針としては、トレンド抽出 → トレンド抜きのデータでモデル作成&予測 → トレンドを戻す
- スパイクが多数存在します。スパイクを考慮せずにデータの平均を取ったりすると、おかしなことになりそう...
トレーニングデータとテストデータに大きな差異がないか確認
train.describe(include='all')

test.describe(include='all')

2. トレンド抽出
販売数のトレンドを抽出します。
statsmodelsのdecomposeを使う手もありますが、今回は最小二乗法によるカーブフィッティングでトレンドを抽出し、それを販売数から引き算することでトレンドを除いた目的変数を作成しました。
また、フィッティングに用いる関数は二次関数を使うより、ある値に漸近する指数関数を使う方が好ましいと考えました。
(販売数の減少量はどこかで飽和すると考えられるので)
from scipy.optimize import curve_fit
def func(x, a, b, c):
return a * np.exp(-b * x) + c
xs = train.index.values
ys = train['y'].values
popt, pcov = curve_fit(func, xs, ys)
a1, b1, c1 = popt
y_reg = a1 * np.exp(-b1 * xs) + c1
plt.figure()
plt.plot(train['y'])
plt.plot(y_reg)
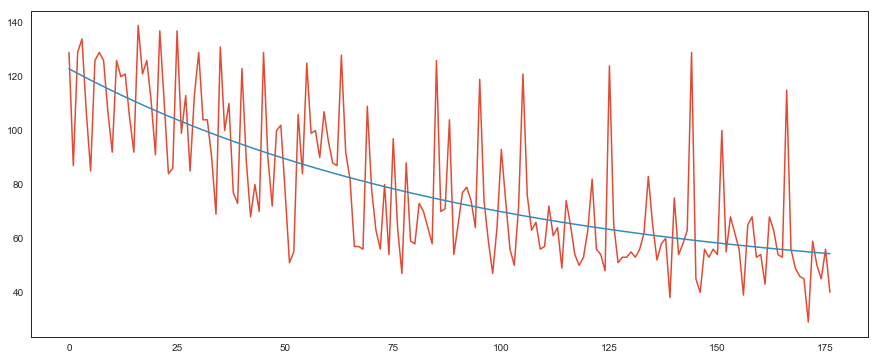
初めの数十レコードを落としたデータに当てはめました。良い感じです。
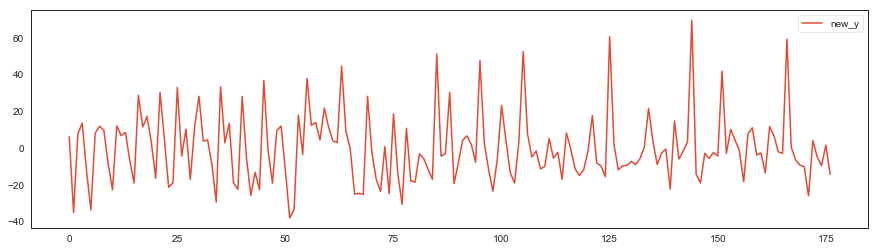
トレンドを除去します。
new_y = train['y'] - y_reg
new_y = pd.DataFrame({'new_y': new_y})
new_y.plot()
3. 特徴量エンジニアリング
説明変数を一つ一つ見ていきます。
datetime
splitして月と日にちの部分だけ使います。
ただ、テストデータにしか存在しない月があるので、学習に月を使うのは微妙と思い今回は落としました。使うにしても加工が必要です。
train['day'] = train['datetime'].apply(lambda x : int(x.split("-")[2]))
「day」と「販売数」の関係性をplotlyで可視化します。
(インタラクティブなグラフなので本来なら触ると統計量を見れるのですが、今回は画像でご勘弁ください...)
import plotly.offline as offline
offline.init_notebook_mode(connected=False)
import plotly.graph_objs as go
layout = go.Layout(
autosize=False,
width=950,
height=500,
margin=go.layout.Margin(
l=80,
r=50,
b=50,
t=10,
pad=4),
xaxis=dict(
title='day',
titlefont=dict(
size=14,
),
showticklabels=True,
tickangle=0,
tickfont=dict(
size=12,
),
),
yaxis=dict(
title='トレンドを除いた販売数',
titlefont=dict(
size=14,
),
showticklabels=True,
tickfont=dict(
size=10,
),
))
data = [go.Box( x=train['day'], y=train['new_y'] )]
fig = go.Figure(data=data, layout=layout)
offline.iplot(fig, filename='example', show_link=False,
config={"displaylogo":False, "modeBarButtonsToRemove":["sendDataToCloud"]})
 plotlyで描画し、17日のBOXを触ってキャプチャしたのが上図です。
グラフを見ると何らかの周期性があり、paydayとの関係性も存在するはずなので残しておきます。
plotlyで描画し、17日のBOXを触ってキャプチャしたのが上図です。
グラフを見ると何らかの周期性があり、paydayとの関係性も存在するはずなので残しておきます。
week
販売数の季節性に大きな影響を与えていそう。
「One hot / Label encoding」か「販売数の Mean/Median encoding」で数値に変換します。
(次元を増やしたくない&スパイクの影響を受けずに周期性を反映させたいので Median encodingしました。)
week_encoded = train.groupby('week').new_y.median()
| week | week_encoded |
|---|---|
| 月 | 7.854857 |
| 木 | -8.968654 |
| 水 | -1.908993 |
| 火 | -3.708110 |
| 金 | -8.816003 |
train['week'] = train['week'].replace(week_encoded)
soldout
「売り切れた日」と「売れ残った日」では販売数の意味合いが違うので、モデルをそれぞれ分けることも考えましたが今回はいっしょくたに作成します。
name
まずは 「name」と「販売数」の関係性を可視化します。
その前に、なるべく純粋な人気度を見たいので、先ほど作成した「week」を引き算し、曜日がもたらす季節性を超簡易的に除去した販売数を用いて可視化します。
train['new_new_y'] = train['new_y'] - train['week']

グラフから読み取れること:
- 人気メニューと不人気メニューがある
- カレーが人気メニューのようにみえる
それぞれについて見ていきます。
まずはカレーから
チュートリアルの通り、「カレー」というワードを含むnameを1、含まないnameを0にラベルづけします。
train['curry'] = train['name'].apply(lambda x : 1 if x.find("カレー") >=0 else 0)

次に人気メニューと不人気メニューをラベル付けします
今回はベースライン(トレンドとweekを差し引いた販売数)から15以上大きいnameを人気メニュー、-15より小さいnameを不人気メニューとしました。
popular_menu = set(train[train['new_new_y']>15].name)
{'さわら焼味噌掛け',
'さんま辛味焼',
'ひやしたぬきうどん・炊き込みご飯',
'キーマカレー',
'サバ焼味噌掛け',
'チキンカレー',
'チンジャオロース',
'チーズハンバーグ',
'ハンバーグカレーソース',
'ポークカレー',
'ポークハヤシ',
'メンチカツ',
'ロコモコ丼',
'手作りロースカツ',
'海老クリーミ―クノーデル',
'牛丼',
'牛肉筍煮',
'豚味噌メンチカツ',
'酢豚',
'酢豚orカレー',
'鶏のピリ辛焼き',
'鶏の唐揚げおろしソース',
'鶏の親子煮',
'鶏チリソース'}
train['popular'] = train['name'].apply(lambda x : 1 if x in popular_menu else 0)
不人気メニューも同様に処理します。
unpopular_menu = set(train[train['new_new_y']<-15].name)
train['unpopular'] = train['name'].apply(lambda x : 1 if x in unpopular_menu else 0)
nameをアノテーションしてみる
次に、トレーニングデータの「name」とテストデータの「name」で積集合を取ってみると、実はテストデータにしか含まれていない「name」が多数あることがわかります。
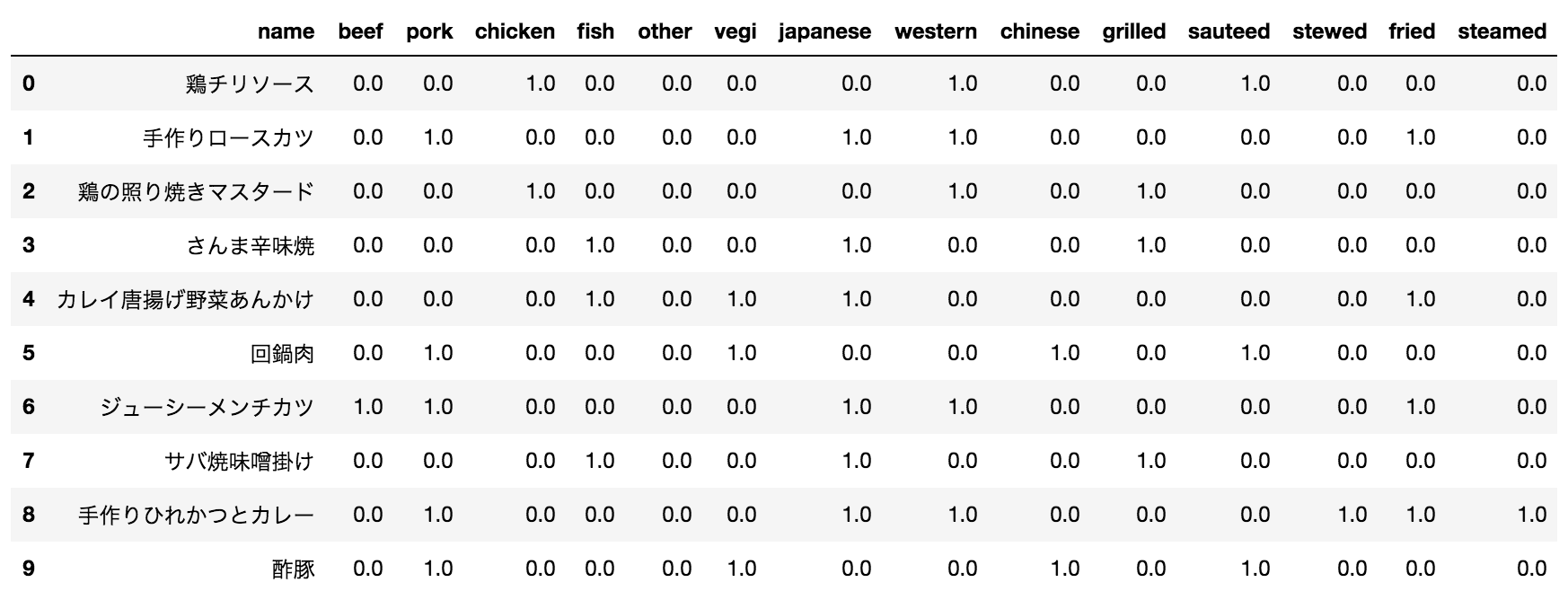
そこで説明力を増すために、以下の変数で「name」を0/1でアノテーションします。
食材: beef、pork、chicken、fish、other(その他魚介)、vegi(野菜)
テイスト: japanese(和風)、western(洋風)、chinese(中華)
調理法: grilled、sauteed、stewed、fried、steamed
-
JanomeやMecabで分かち書き→Word2vecなどでベクトル化する方法もたくさんあると思いますが、マニュアルでアノテーションした方が今回はお弁当の特徴をうまく表現できると思いました...ただしデータ数が少ない場合にしかできませんが...
-
また、この弁当名のベクトル化は前述の「popular」「unpopular」よりも汎用的なエンコーディングになっているので、モデルの汎化性能を高めているはずです。
kcal
欠損値が存在するので、トレーニングデータ全体の平均値で補間します。
train['kcal'] = train['kcal'].fillna(train['kcal'].mean())
remarks と event
情報量は少ないですが、重要な情報がないか精査します。
まずは「remarks」と「販売数」の関係性を可視化します。
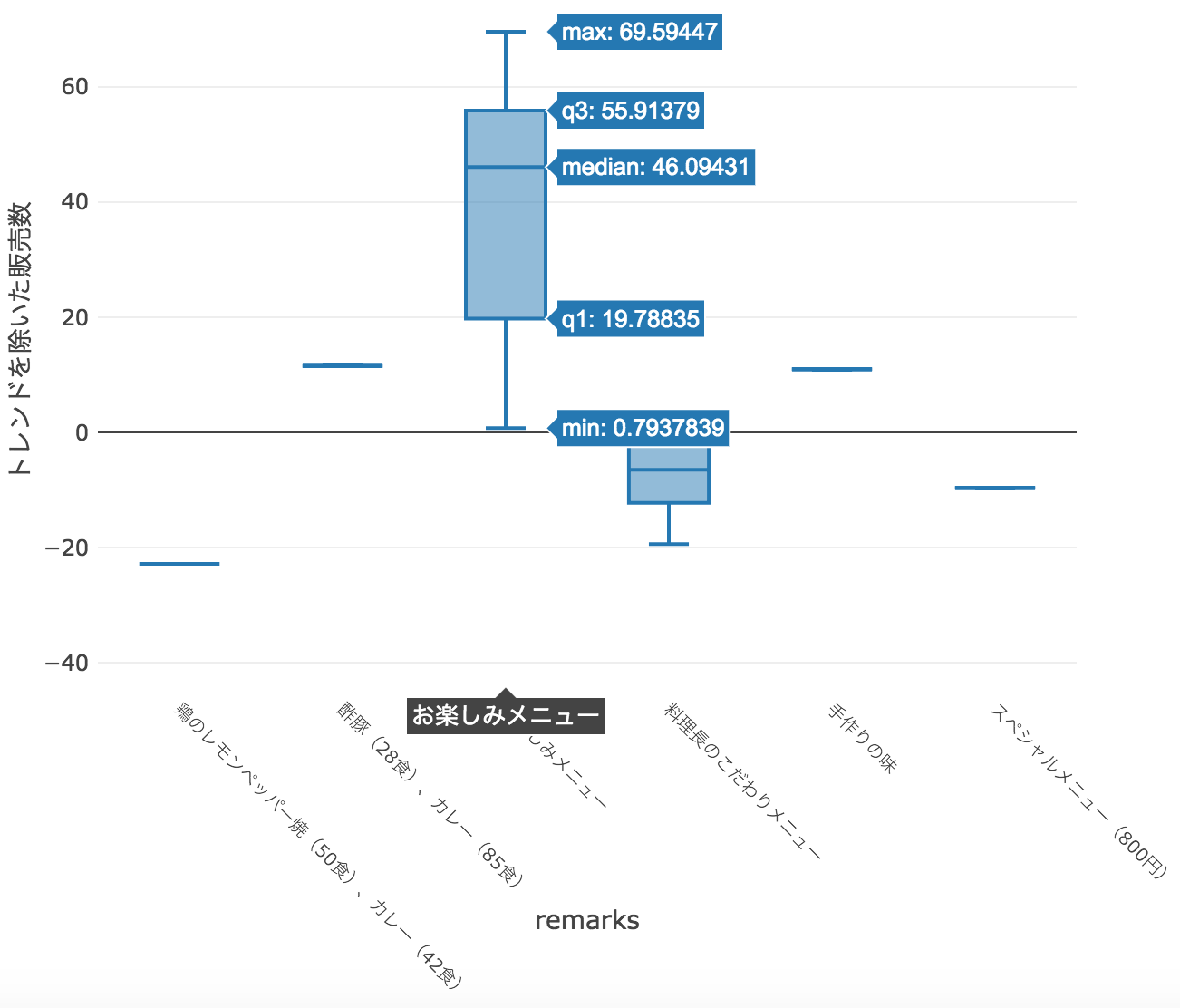
お楽しみメニューが大人気なので、特徴量に加えます。
単純に「お楽しみメニュー」に合致するremarksを1、それ以外を0にラベルづけします。
train['fun'] = train['remarks'].apply(lambda x: 1 if x=="お楽しみメニュー" else 0)
eventも同様に可視化しましたが、特に情報がなかったので今回は落とします。
payday
給料日の前後で販売数の傾向が異なると予想されます。今回は0/1ラベルでそのまま使用しました。
train['payday'] = train['payday'].fillna(0)
weather
「One hot / Label encoding」か「販売数の Mean/Median encoding」で数値に変換します。
次元が増えると嫌なので、「快晴」「晴れ」「曇」「雨およびその他」の4種で Median encoding しました。
weather_word = ['快晴','晴','曇','雨','雪','雷']
row_index = []
number = 1
for x in weather_word:
row_index = train['weather'].str.contains(x, na=False)
train.loc[row_index, ['weather']] = number
if number < 4:
number += 1
else:
number = 4
row_index = []
weather_encoded = train.groupby('weather').new_y.median()
train['weather'] = train['weather'].replace(weather_encoded)
precipitation
言わずもがなweatherと相関があるので、今回は落としました。
train = train.drop(columns = ['precipitation'])
temperature
そのままでも使えそうですが、前日との差分や月平均との差分を取ったほうが説明力が高いと考えました。
そこで今回は月平均との差分を「temp」として説明変数に加えました。
(「暖かい日が続いたが、ある日突然冷え込むとその日は外に出たくなくなる」みたいなことがあるので、販売数との相関がありそうと考えた。)
train['month'] = train['datetime'].apply(lambda x : int(x.split("-")[1]))
temp_mean = train.groupby('month').temperature.mean()
train['month'] = train['month'].replace(temp_mean)
train['temp'] = train['temperature'] - train['month']
最後に、pairplotを作成しましょう
外れ値の有無や、目的変数との相関を可視化して確認します。
今回は極端な外れ値がなかったため、そのまま使用します。
4. 特徴選択
どの特徴量をモデルに採用するか取捨選択します。
やり方は色々あります。
- 説明変数と目的変数の相関をみて選択する(特徴量同士の相関が強い場合、どちらか落とすことも)
- RandomForest系の学習器を用いて重要度を算出し、選択する
- SBSアルゴリズムを用いて選択する
- 直感的に重要だと感じる特徴量を入れてみて試行錯誤する
今回はRandomForestの重要度を用いて特徴量を選定しました。
こちらの投稿が大変参考になります。
(XGBoostやLightGBMを用いて特徴量の重要度を算出することもできますが、それらの重要度に従って特徴量を採用しても今回はあまり精度が上がりませんでした。この辺りは試行錯誤かなと思います...)
base = ['soldout','kcal','day','payday','temperature','temp']
weather = ['weather']
week = ['week']
name = ['fun','curry','popular','unpopular']
annotation = ['beef','pork','chicken','fish','other','vegi','japanese','chinese',
'western','grilled','sauteed','stewed','fried','steamed']
feature_x = base + weather + week + name + annotation
feature_y = ['new_y']
data_x = train[feature_x]
data_y = train[feature_y]
from sklearn.ensemble import RandomForestRegressor
rf_reg = RandomForestRegressor(n_estimators=10000)
rf_reg = rf_reg.fit(data_x, data_y)
fti = rf_reg.feature_importances_
dic_arr = {'importance':fti, 'feature':feature_x}
pd.DataFrame(dic_arr).sort_values('importance', ascending=False).reset_index(drop=True).loc[:15, :]
| feature | importance | |
|---|---|---|
| 0 | popular | 0.247882 |
| 1 | fun | 0.178017 |
| 2 | week | 0.114100 |
| 3 | unpopular | 0.113638 |
| 4 | temperature | 0.086833 |
| 5 | day | 0.057744 |
| 6 | temp | 0.047977 |
| 7 | curry | 0.032029 |
| 8 | kcal | 0.030388 |
| 9 | beef | 0.015847 |
| 10 | western | 0.011213 |
| 11 | weather | 0.009339 |
| 12 | japanese | 0.007453 |
| 13 | soldout | 0.006305 |
| 14 | payday | 0.006071 |
| 15 | pork | 0.005581 |
今回はシンプルに、RandomForestの重要度が上位16の特徴量をそのまま入力しました。
(今回のRandomForestによる重要度算出では n_estimatorsを10000以上に設定すると、だいたいいつも同じ特徴量が顔を出すようになりました。)
5. モデル作成
学習器ですが、今回はオーソドックスにXGBoostとLightGBMでモデルを作成しました。
結果的にLightGBMの方が精度が良かったため、そちらを採用しました。
(XGBoostは今回のトレーニングデータに容易にoverfitしてしまい、それを抑えるのが難しかったです...)
コーディングはこちらのサイトを参考にしています。
※ 本来ならば、時系列データの交差検証で ShuffleSplit してしまうのは宜しくないと思います。しかし、今回はトレンドを除去し、季節性を説明する「week」や「day」も特徴に加えたので、シャッフルしてもなんとかなると考えました...
パラメータ調整
勾配ブースティング木系学習器チューニングのベストプラクティスは有名なものがあるので、そちらを参考に調整しました。
手順は以下の通りです。
1. 大きめの学習率(0.1くらい)で最適な木の数(n_estimators)を決定する
2. 木に関するパラメータ(colsample_bytree, max_depth, subsample など)をチューニングする
3. 正則化パラメータ(reg_alpha, reg_lambda)をチューニングする
4. より小さい学習率で最適な木の数を決定する
詳しくはこちらのリンクをご覧ください!
LGBMR = lgb.LGBMRegressor()
cv_split = model_selection.ShuffleSplit(n_splits = 10, test_size = .3, train_size = .7,
random_state = 0 )
base_results = model_selection.cross_validate(LGBMR, data_x[feature_x], data_y[feature_y],
scoring = 'mean_squared_error', cv = cv_split)
LGBMR.fit(data_x[feature_x], data_y[feature_y])
print("Training score mean: {:.2f}". format
(np.sqrt(abs(tune_model.cv_results_['mean_train_score'][tune_model.best_index_]))))
print("Test score mean: {:.2f}". format
(np.sqrt(abs(tune_model.cv_results_['mean_test_score'][tune_model.best_index_]))))
パラメータ調整前のRMSE:
Training score mean: 7.86
Test score mean: 12.74
param_grid = {'boosting_type': ['gbdt'],
'class_weight': [None],
'colsample_bytree': [0.9],
'importance_type': ['split'],
'learning_rate': [0.05],
'max_depth': [2],
'min_child_samples': [2],
'min_child_weight': [0],
'min_split_gain': [0],
'n_estimators': [200],
'n_jobs': [-1],
'num_leaves': [3],
'objective': [None],
'random_state': [None],
'reg_alpha': [0.01],
'reg_lambda': [0.01],
'silent': [True],
'subsample': [0.1],
'subsample_freq': [0]}
tune_model = model_selection.GridSearchCV(lgb.LGBMRegressor(), param_grid=param_grid,
scoring = 'mean_squared_error', cv = cv_split)
tune_model.fit(data_x[feature_x], data_y[feature_y])
print("Training score mean: {:.5f}". format
(np.sqrt(abs(tune_model.cv_results_['mean_train_score'][tune_model.best_index_]))))
print("Test score mean: {:.5f}". format
(np.sqrt(abs(tune_model.cv_results_['mean_test_score'][tune_model.best_index_]))))
パラメータ調整後のRMSE:
Training score mean: 6.75292
Test score mean: 10.72868
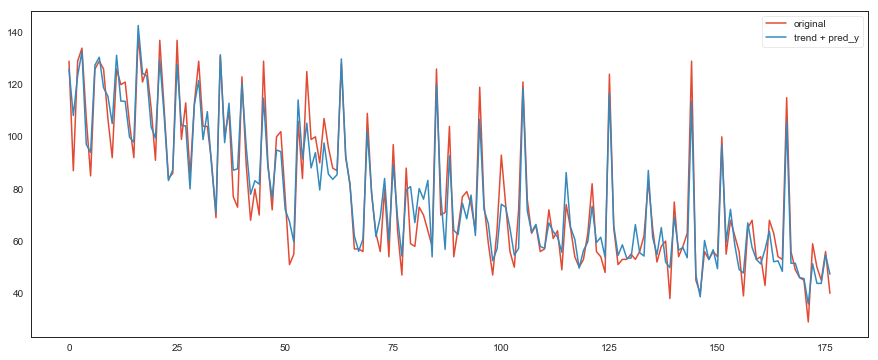
試しに、作成したモデルをトレーニングデータに当てはめてみます
train['new_y'] = tune_model.predict(data_x[feature_x])
original = train['y']
pred_y = train['new_y']
final_train = y_reg + pred_y
plt.figure()
plt.plot(original, label='original', linestyle='-')
plt.plot(final_train, label='trend + pred_y', linestyle='-')
plt.legend(loc='best')
6. テストデータの前処理と予測
テストデータをトレーニングデータと同様に前処理します。
「week」のようにカテゴリカルデータを数値にエンコーディングした場合は、以下のようにトレーニングデータと同じエンコード対応表を用いて処理します。
test['week'] = test['week'].replace(week_encoded)
test['weather'] = test['weather'].replace(weather_encoded)
test['popular'] = test['name'].apply(lambda x : 1 if x in popular_menu else 0)
test['unpopular'] = test['name'].apply(lambda x : 1 if x in unpopular_menu else 0)
最後に、作成したモデルをテストデータに適用します。
data_x = test
test['y'] = tune_model.predict(data_x[feature_x])
トレンドの関数も外挿する感じでテストデータに当てはめ、テストデータのトレンド成分を予測、最後にそれを足し算します。
test['index_new'] = test.index + train.index.max() + 1
xs = test['index_new'].values
y_reg = a1 * np.exp(-b1 * xs) + c1
test['y'] = test['y'] + y_reg
あとは提出用データを作成するだけです!
まとめ
独特なアノテーション以外はベーシックな手法だけで予測できていると思います。
参考になれば幸いです。
※ 不足点のご指摘もお待ちしております。
参考文献
お弁当の需要予測チュートリアル
ランダムフォレスト系ツールで特徴量の重要度を測る
A Data Science Framework: To Achieve 99% Accuracy
Complete Guide to Parameter Tuning in XGBoost (with codes in Python)
[Python] Plotlyでぐりぐり動かせるグラフを作る