はじめに
複数の特徴量を含むデータセットを分析する際,ランダムフォレストに代表される決定木ベースのアンサンブル分析器では,特徴量の重要度を算出することができます.これまで,私はブラックボックスとしてこの機能を使ってきましたが,使うツールが増えてきたので,少し使い方を整理したいと思います.
まず重要度算出のアルゴリズムですが,"はじめてのパターン認識"(11章)から引用させていただきます.
Out-Of-Bag(OOB) 誤り率は次のように計算する.ランダムフォレストは,一つの木を作るときにブートストラップにより使用する学習データを選んでいる.その結果,約1/3のデータは学習に使われない.ある学習について,その学習データが使われなかった決定木のみを集めて部分森を構成し,その学習データをテストデータにして誤りを評価することができる.
決定木ベースのアンサンブルを行う際,上記の方法でOOB誤り率をモニターすることで,精度upに結びつく特徴量の重要度が測定できるということのようです.
以下,次のツール(Python package)を見ていきます.
- Scikit-learn の RandomForest
- XGBoost
- LightGBM
XGBoostとLightGBMは,よりネイティブに近いAPIと,Scikit-learn APIがありますが,学習の効率を考え極力,Scikit-learn APIを使っていきたいと思います.
(用いたツール,ライブラリは次の通りです.Python 3.5.2, Scikit-learn 0.18.1, XGBoost 0.6a2, LightGBM 0.1 )
Scikit-learn の RandomForest
まずは,基本形になります.
分類問題
import numpy as np
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.ensemble import RandomForestClassifier
iris = load_iris()
X = iris.data
y = iris.target
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=0)
clf_rf = RandomForestClassifier()
clf_rf.fit(X_train, y_train)
y_pred = clf_rf.predict(X_test)
accu = accuracy_score(y_test, y_pred)
print('accuracy = {:>.4f}'.format(accu))
# Feature Importance
fti = clf_rf.feature_importances_
print('Feature Importances:')
for i, feat in enumerate(iris['feature_names']):
print('\t{0:20s} : {1:>.6f}'.format(feat, fti[i]))
よくご存知の方も多いと思いますが,分類器のインスタンスを定義し,fit() 後,feature_importances_の数値を得るだけです.
Feature Importances:
sepal length (cm) : 0.074236
sepal width (cm) : 0.015321
petal length (cm) : 0.475880
petal width (cm) : 0.434563
上記のように "iris" データセットでは,"petal" 関係の特徴量が重要との結果が得られました.(この重要度は,相対的な数値になります.)
回帰問題
Scikit-learn についてくる"Boston"データセットを扱いました.
rf_reg = RandomForestRegressor(n_estimators=10)
rf_reg = rf_reg.fit(X_train, y_train)
fti = rf_reg.feature_importances_
print('Feature Importances:')
for i, feat in enumerate(boston['feature_names']):
print('\t{0:10s} : {1:>.6f}'.format(feat, fti[i]))
関数名が RandomForestRegressor() に変わりますが,特徴量の重要度算出は同じやり方です.
Feature Importances:
CRIM : 0.040931
ZN : 0.001622
INDUS : 0.005131
CHAS : 0.000817
NOX : 0.042200
RM : 0.536127
AGE : 0.018797
DIS : 0.054397
RAD : 0.001860
TAX : 0.010357
PTRATIO : 0.011388
B : 0.007795
LSTAT : 0.268579
回帰問題でも分類問題と同様のやり方で"Feature Importances"が得られました."Boston" データセットでは,"RM", "LSTAT" のfeatureが重要との結果です.(今回は,「特徴量重要度を求める」という主旨につき,ハイパーパラメータの調整は,ほとんど行っていませんので注意願います.)
XGBoost の分類器,回帰器
Gradient Boosting の代表格,XGBoostのやり方を確認します.
分類問題
clf_xgb = xgb.XGBClassifier(objective='multi:softmax',
max_depth = 5,
learning_rate=0.1,
n_estimators=100)
clf_xgb.fit(X_train, y_train,
eval_set=[(X_test, y_test)],
eval_metric='mlogloss',
early_stopping_rounds=10)
y_pred_proba = clf_xgb.predict_proba(X_test)
y_pred = np.argmax(y_pred_proba, axis=1)
accu = accuracy_score(y_test, y_pred)
print('accuracy = {:>.4f}'.format(accu))
# Feature Importance
fti = clf_xgb.feature_importances_
print('Feature Importances:')
for i, feat in enumerate(iris['feature_names']):
print('\t{0:20s} : {1:>.6f}'.format(feat, fti[i]))
Scikit-learn APIが使えますので,前述の RandomForestClassifier と全く同じやり方でFeature Importance を求めることができました.
回帰問題
こちらも分類と同様,Scikit-learn APIを使いたかったのですが,feature importances の算出は,現時点で未サポートのようです.GitHubに open issue としてあがっていました.
代わりに,XGBoost のネイティブに近い方のAPIを使います.
'''
# Error
reg_xgb = xgb.XGBRegressor(max_depth=3)
reg_xgb.fit(X_train, y_train)
fti = reg_xgb.feature_importances_
'''
def create_feature_map(features):
outfile = open('boston_xgb.fmap', 'w')
i = 0
for feat in features:
outfile.write('{0}\t{1}\tq\n'.format(i, feat))
i = i + 1
outfile.close()
create_feature_map(boston['feature_names'])
xgb_params = {"objective": "reg:linear", "eta": 0.1, "max_depth": 6, "silent": 1}
num_rounds = 100
dtrain = xgb.DMatrix(X_train, label=y_train)
gbdt = xgb.train(xgb_params, dtrain, num_rounds)
fti = gbdt.get_fscore(fmap='boston_xgb.fmap')
print('Feature Importances:')
for feat in boston['feature_names']:
print('\t{0:10s} : {1:>12.4f}'.format(feat, fti[feat]))
一度,feature map のファイルに出力してから処理しています.上記により以下の結果が得られました.
Feature Importances:
CRIM : 565.0000
ZN : 55.0000
INDUS : 99.0000
CHAS : 10.0000
NOX : 191.0000
RM : 377.0000
AGE : 268.0000
DIS : 309.0000
RAD : 50.0000
TAX : 88.0000
PTRATIO : 94.0000
B : 193.0000
LSTAT : 285.0000
Scikit-learn RandomForestRegressor の結果と一部,整合性がないところがありますが,パラメータの調整不足に起因していると予想されます.
LightGBM の分類器,回帰器
こちらは,分類/回帰とも Scikit-learn APIが使えました.
分類
gbm = lgb.LGBMClassifier(objective='multiclass',
num_leaves = 23,
learning_rate=0.1,
n_estimators=100)
gbm.fit(X_train, y_train,
eval_set=[(X_test, y_test)],
eval_metric='multi_logloss',
early_stopping_rounds=10)
y_pred = gbm.predict(X_test, num_iteration=gbm.best_iteration)
y_pred_proba = gbm.predict_proba(X_test, num_iteration=gbm.best_iteration)
accu = accuracy_score(y_test, y_pred)
print('accuracy = {:>.4f}'.format(accu))
# Feature Importance
fti = gbm.feature_importances_
print('Feature Importances:')
for i, feat in enumerate(iris['feature_names']):
print('\t{0:20s} : {1:>.6f}'.format(feat, fti[i]))
回帰
gbm_reg = lgb.LGBMRegressor(objective='regression',
num_leaves = 31,
n_estimators=100)
gbm_reg.fit(X_train, y_train,
eval_set=[(X_test, y_test)],
eval_metric='l2',
verbose=0)
# Feature Importances
fti = gbm_reg.feature_importances_
print('Feature Importances:')
for i, feat in enumerate(boston['feature_names']):
print('\t{0:10s} : {1:>12.4f}'.format(feat, fti[i]))
まだ,「若い」ツールですが LightGBM 便利!
以上,3種類のツールを見てきました.特徴量の重要度は,似た傾向を示しています.一部,整合性がない部分は,(繰り返しになりますが)ハイパーパラメータの調整不足によるものと考えています.
(補足)統計モデリングにおけるp値との関係
補足というか,気になったので統計モデリングにおける「特徴量の選択」について少し考えてみました.正しいやり方としては,データ特徴量のサブセットに対応した複数のモデルを作成して,データにfitさせ,各モデルのモデル選択基準(例えばAIC,Akaike's information criterion)の値を比較することになると思います.しかし,一回の処理で全特徴量の影響度を求めることはできません.
ところで,一回のモデリング計算時に算出される値として,p値(あるいはz値)があります.この数値とランダムフォレスト系ツールのFeature Importanceに何か関係性があるのか,少し見ていきたいと思います.
統計モデリングのツールは StatsModels を使いました.久しぶりに使おうとしたところ,バージョン 0.8.0がリリースされていました.(開発中だった 0.7.x は,リリースがスキップされたようです.また,ドキュメントも以前はSourceForgeにありましたが,0.8.0 では,別のサイト http://www.statsmodels.org/stable/ に移動していました.)
"Boston" の線形回帰モデル
import statsmodels.api as sm
from sklearn.datasets import load_boston
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import KFold, train_test_split
print("Boston Housing: regression")
boston = load_boston()
y = boston['target']
X = boston['data']
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.33, random_state=201703
)
# Using StatsModels
X1_train = sm.add_constant(X_train)
X1_test = sm.add_constant(X_test)
model = sm.OLS(y_train, X1_train)
fitted = model.fit()
print('summary = \n', fitted.summary())
上記コードにおける summary は,以下のようになりました.
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.758
Model: OLS Adj. R-squared: 0.749
Method: Least Squares F-statistic: 78.38
Date: Fri, 10 Mar 2017 Prob (F-statistic): 8.08e-92
Time: 15:14:41 Log-Likelihood: -1011.3
No. Observations: 339 AIC: 2051.
Df Residuals: 325 BIC: 2104.
Df Model: 13
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 38.3323 6.455 5.939 0.000 25.634 51.031
x1 -0.1027 0.035 -2.900 0.004 -0.172 -0.033
x2 0.0375 0.018 2.103 0.036 0.002 0.073
x3 0.0161 0.081 0.198 0.843 -0.144 0.176
x4 2.8480 1.058 2.692 0.007 0.767 4.929
x5 -19.4905 5.103 -3.819 0.000 -29.530 -9.451
x6 3.9906 0.501 7.973 0.000 3.006 4.975
x7 0.0004 0.016 0.024 0.980 -0.031 0.032
x8 -1.5980 0.256 -6.236 0.000 -2.102 -1.094
x9 0.3687 0.090 4.099 0.000 0.192 0.546
x10 -0.0139 0.005 -2.667 0.008 -0.024 -0.004
x11 -0.9445 0.167 -5.640 0.000 -1.274 -0.615
x12 0.0086 0.004 2.444 0.015 0.002 0.015
x13 -0.6182 0.063 -9.777 0.000 -0.743 -0.494
==============================================================================
Omnibus: 115.727 Durbin-Watson: 2.041
Prob(Omnibus): 0.000 Jarque-Bera (JB): 485.421
Skew: 1.416 Prob(JB): 3.91e-106
Kurtosis: 8.133 Cond. No. 1.53e+04
==============================================================================
主な統計情報が出力されましたが,今回はp値に着目したいと思います.以下のコードで出力しました.
pvalues = fitted.pvalues
feats = boston['feature_names']
print('P>|t| :')
for i, feat in enumerate(feats):
print('\t{0:10s} : {1:>.6f}'.format(feat, pvalues[(i + 1)]))
P>|t| :
CRIM : 0.003980
ZN : 0.036198
INDUS : 0.843357
CHAS : 0.007475
NOX : 0.000160
RM : 0.000000
AGE : 0.980493
DIS : 0.000000
RAD : 0.000053
TAX : 0.008030
PTRATIO : 0.000000
B : 0.015065
LSTAT : 0.000000
13の特徴量の内,"INDUS", "AGE"が1.0に近い数値,それ意外はすべて0.05以下に収まっています.
これと,LightGBMで求めたFeature Importanceとの関係を見るためプロットしてみました.
Fig.1 Feature Importance vs. StatsModels' p-value
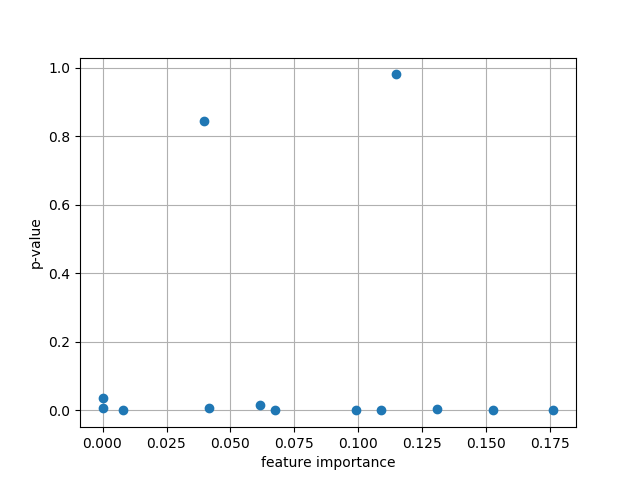
縦軸を拡大し,y=0 近傍を見てみます.
Fig.2 Feature Importance vs. StatsModels' p-value
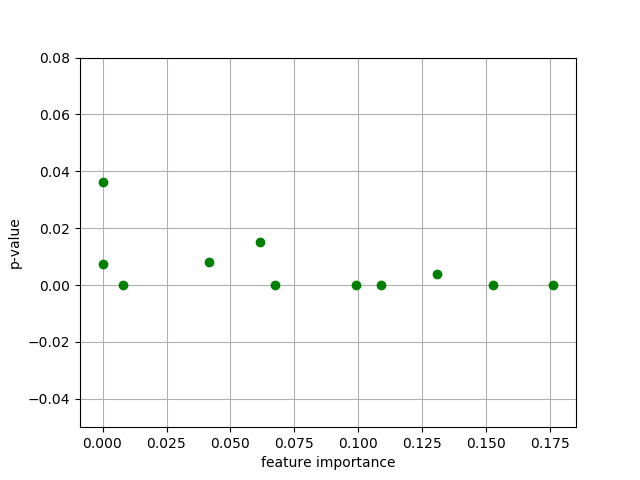
横軸にFeature Importance, 縦軸に p-valueをとりました.ここのエリアでは,横軸が大きくなるにつれ,縦軸のばらつきが減っているように見えます.
"Titanic" の分類問題
次に Kaggle で取り上げられた"Titanic"の分類問題(二値分類)を調べてみました.以下のように,StatsModelsのロジスティック回帰を実施しました.
import statsmodels.api as sm
# by StatsModels
X_train = sm.add_constant(X_train)
X_test = sm.add_constant(X_test)
model_lr = sm.Logit(y_train, X_train)
res = model_lr.fit()
print('res.summary = ', res.summary())
y_pred = res.predict(X_test)
y_pred = np.asarray([int(y_i > 0.5) for y_i in y_pred])
# check feature importance
pvalues = res.pvalues
print('P>|z|:')
for i, feat in enumerate(feats):
print('\t{0:15s} : {1:>12.4f}'.format(feat, pvalues[i]))
上記の通り sm.Logit() を用いています.結果は,次のようになりました.
Logit Regression Results
==============================================================================
Dep. Variable: y No. Observations: 668
Model: Logit Df Residuals: 657
Method: MLE Df Model: 10
Date: Fri, 10 Mar 2017 Pseudo R-squ.: 0.3219
Time: 15:36:15 Log-Likelihood: -305.07
converged: True LL-Null: -449.89
LLR p-value: 2.391e-56
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 1.2615 8.99e+06 1.4e-07 1.000 -1.76e+07 1.76e+07
x1 0.0001 0.000 0.309 0.758 -0.001 0.001
x2 -0.9141 0.162 -5.644 0.000 -1.232 -0.597
x3 2.7590 0.231 11.939 0.000 2.306 3.212
x4 -0.0322 0.009 -3.657 0.000 -0.049 -0.015
x5 -0.4421 0.132 -3.350 0.001 -0.701 -0.183
x6 -0.0709 0.141 -0.503 0.615 -0.347 0.206
x7 2.456e-07 1.77e-07 1.386 0.166 -1.02e-07 5.93e-07
x8 0.0023 0.003 0.926 0.354 -0.003 0.007
x9 0.6809 8.99e+06 7.57e-08 1.000 -1.76e+07 1.76e+07
x10 0.3574 8.99e+06 3.97e-08 1.000 -1.76e+07 1.76e+07
x11 0.2231 8.99e+06 2.48e-08 1.000 -1.76e+07 1.76e+07
==============================================================================
P>|z|:
PassengerId : 1.0000
Pclass : 0.7575
Sex : 0.0000
Age : 0.0000
SibSp : 0.0003
Parch : 0.0008
Ticket : 0.6151
Fare : 0.1657
C : 0.3543
Q : 1.0000
S : 1.0000
モデルに入れるまでのデータ前処理については説明を省略しますが,データセットにあった "Embarked"
(乗船した港)については,One-Hotエンコードにより ['C','Q','S'] の3特徴量に変化しています.
("Embarked"は,予想通り,あまり重要な特徴量ではありませんでした.)
今度もLightGBMの結果とつき合わせてみます.横軸が,LightGBMの Feature Importance,縦軸が p-value になります.
Fig.3 Feature Importance vs. StatsModels' p-value
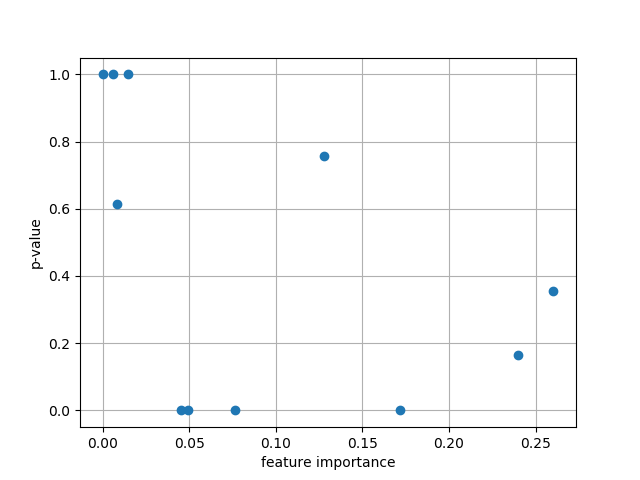
機械学習,特に決定木アンサンブル系のモデルと統計モデリングのコンセプトは全く異なるので,
各プロット(Fig.1, 2, 3)で相関を見ようとするのには,無理があるのかも知れません.
- Feature Importance : 学習過程でOut-of-Bag誤り率低減に寄与する特徴量の効果
- P-value : 当てはめた統計モデル(母集団)に対してデータサンプルがきれいに収まっているかどうかの指標
これは私のあいまいな理解ですが,2つの数字は異なったコンセプトに基づいています.しかしながら,全くの無関係なものではなく,(状況によりますが)p-valueがある程度小さくならないとFeature Importanceが上がってこない,といった因果関係があるのかも知れないと想像しています.(根拠もなく,あくまで想像です.)
また「良いモデル」を得るという目的において,「有効な特徴量はそのままモデルに組み込む」,「有効でないものや,p値が小さくない特徴量については,前処理,あるいはモデルを改良する」,「見込みがないものは捨てる」というアプローチは,どちらのモデリング手法においても大事であると感じています.
参考文献,web site
- はじめてのパターン認識,平井氏著,森北出版
- データ解析のための統計モデリング入門,久保氏著,岩波書店
- Scikit-learn Documentation - http://scikit-learn.org/stable/documentation.html
- XGBoost Documentation - https://xgboost.readthedocs.io/en/latest/
- LightGBM Documentation - https://github.com/Microsoft/LightGBM/tree/master/python-package
- StatsModels Documentation - http://www.statsmodels.org/stable/index.html