階層ベイズで個性を捉える(PyMC ver.5.7.2)

はじめに

あまりベイズモデリングを勉強していなかった私。
なんとなくどういった場面で使うべきか思いつかなかったから。
いくつか本は持っていたが、積んだまま。
そんな時に以下の資料を見た。

• GLMMの紹介 GLM→GLMM→階層ベイズモデル
• 階層ベイズによるワンToワンマーケティング入門

「え、個体ごとにパラメータ出せるんだ！？めっちゃええやん。」

特にOne-To-Oneマーケティングが可能ってことが魅力的だった。たまにマーケティング関連の分析をすることもあり、クラスタリングでマイクロマーケティングなら実践したことがあったので、いっちょ勉強してみっか！と動き出したのだった。
てか階層ベイズのお勉強して思ったが、SEMとかもやろうと思えばベイズモデル化できるんだよな、多分。

今回は仮想購買データを使って、階層ベイズモデルを構築し、個人ごとに良さげなパラメータが求められているか確認してみる。
今回の作業の流れとしては、まずscikit-learnのロジスティック回帰でモデル作る、その後ベイズロジスティック回帰、階層ベイズ二項ロジットモデルと順に作って結果を見る。階層ベイズ二項ロジットモデルは3パターン作った。

1. scikit-learnのロジスティック回帰モデル
2. ベイズロジスティック回帰モデル
3. 階層ベイズ二項ロジットモデル: 属性情報なし 固定効果あり ランダム効果あり
4. 階層ベイズ二項ロジットモデル: 属性情報あり 固定効果あり ランダム効果あり
5. 階層ベイズ二項ロジットモデル: 属性情報あり 固定効果なし ランダム効果あり

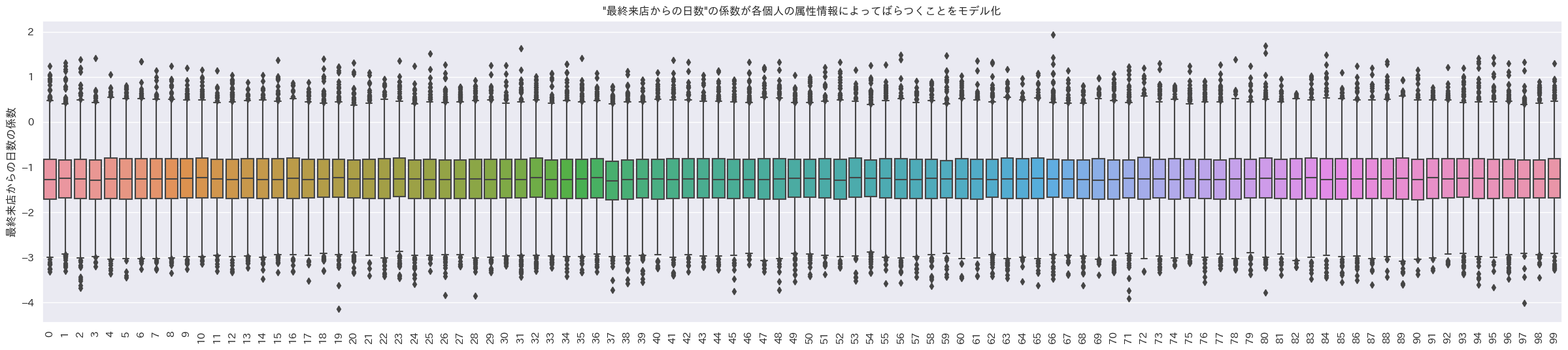
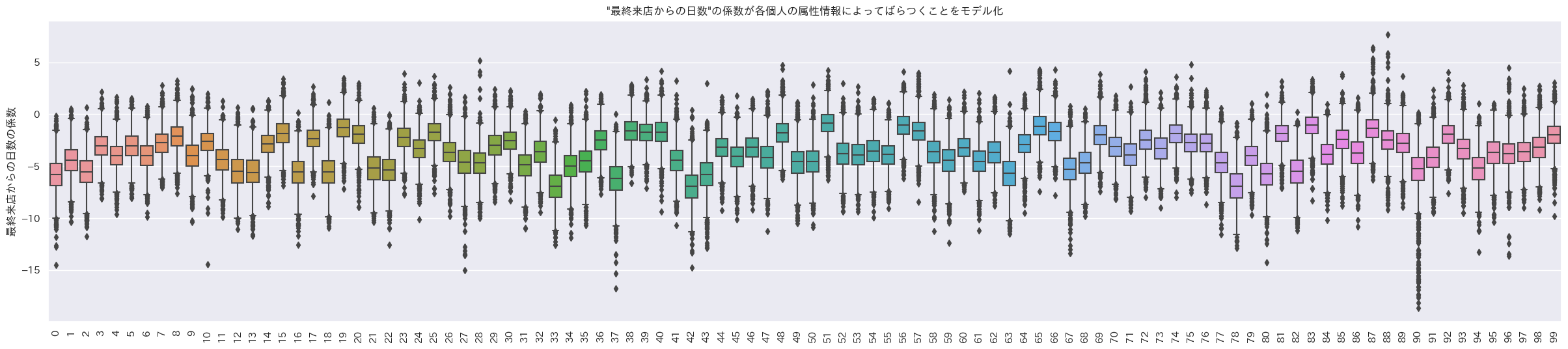
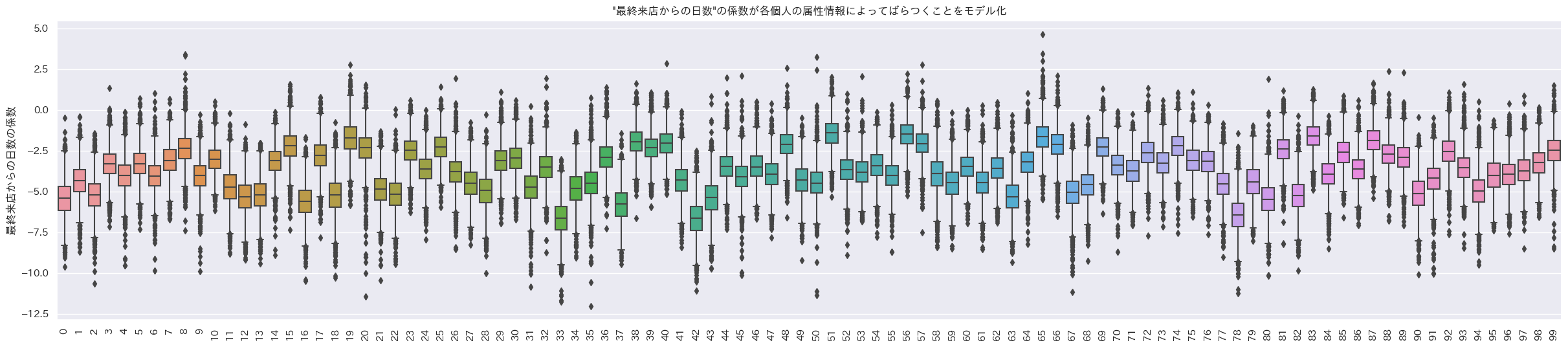
階層ベイズ二項ロジットモデルでは個人単位でパラメータを推定できるので、例えば今回の結果の一部である以下の画像のように、ある変数の係数の分布を個人ごとに求めることができる。（図：変数"最終来店日からの日数"の係数の箱ひげ図。横軸は各個人を表す。）

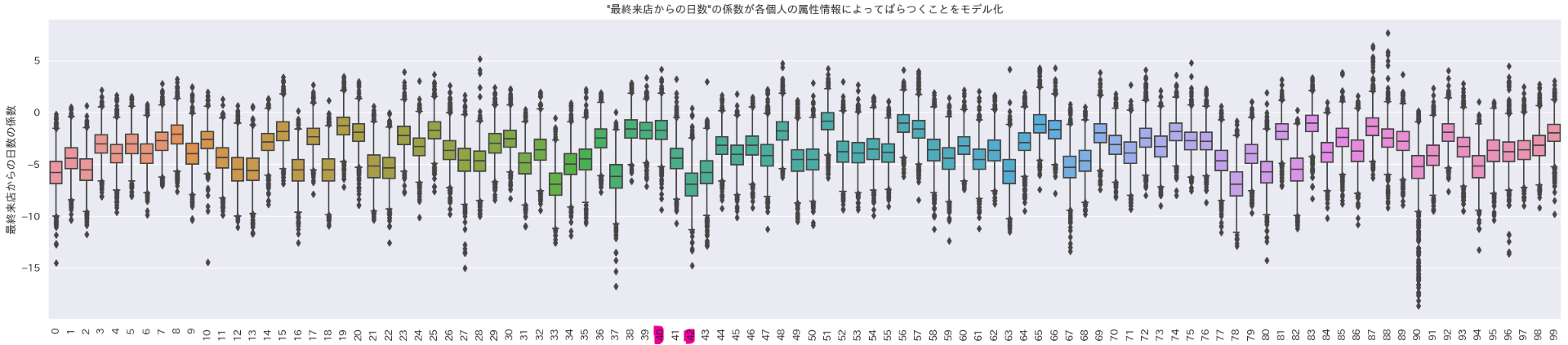
図を見ると42番さんは40番さんに比べて"最終来店日からの日数"の影響が負の方向にかなり大きいとかわかる。すばらしいね。

というわけでやってみたことを書いていく。

参考

• [書籍]Pythonではじめるベイズ機械学習入門
• 「Pythonではじめるベイズ機械学習入門」のNotebook(著者のgithub)
• [書籍]実践Data Scienceシリーズ RとStanではじめる ベイズ統計モデリングによるデータ分析入門
• GLMMの紹介 GLM→GLMM→階層ベイズモデル
• 階層ベイズによるワンToワンマーケティング入門
• 8行のデータで理解する階層ベイズ
• pymc公式
• PyMC：重回帰を題材にしたPyMCの紹介
• Bayesian Statistics and Marketingの5章 – 家計の異質性を考慮した階層ベイズモデル
• Bayesian Statistics and Marketing – 混合ガウス×階層モデルのマーガリン購買データへの適用
• The PyMC3 workflow
• PyMCでの階層モデルの実装例
• 階層モデルの分散パラメータの事前分布について発表しました
• ロバストなベイズ的回帰分析のための新しい誤差分布 (理論編)
• MCMCとともだちになろう
• Stanを使ってNUTSを実装する

各パッケージインポート

作業環境はJupyterlab。
今回pymcを使って階層ベイズモデルを作る。
まず、pymc関連以外で必要なパッケージをインポート。

# 使わないやつもimportしてると思う
import os
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
from matplotlib import cm
import matplotlib.font_manager as fm
import sklearn
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import recall_score, precision_score, f1_score, accuracy_score, confusion_matrix
from sklearn.model_selection import train_test_split
import scipy
from scipy.spatial import distance
import seaborn as sns
import tqdm as tq
from tqdm import tqdm
import gzip
import glob
import datetime as dt
import shutil
import collections
import functools
import gc
import sys
import time
import pickle
import zipfile
import json
import lightgbm as lgb

# matplotlib日本語plot用
jpn_fonts=list(np.sort([ttf for ttf in fm.findSystemFonts() if 'ipaexg' in ttf or 'msgothic' in ttf or 'japan' in ttf or 'ipafont' in ttf]))
jpn_font=jpn_fonts[0]
prop = fm.FontProperties(fname=jpn_font)
print(jpn_font)
sns.set()

そしてベイズモデリングのためのパッケージを入れるのだが、今回はGPUを使わずCPUだけ使い、複数の論理プロセッサを使いたいので、使用するプロセッサ数を指定。
指定後、数値計算ライブラリjaxで使用する論理プロセッサ数が指定した数だけあることを確認。

# CPU Multi
os.environ["XLA_FLAGS"] = '--xla_force_host_platform_device_count=8'

import jax
print(jax.default_backend())
print(jax.devices("cpu"))

これでOK。実は最初にこれを指定せずにやってたらMCMCが遅すぎて途方に暮れてた。3つのチェーンでサンプリングをしていたが、1つずつしか計算してくれなくて時間かかりすぎてた…。

次にpymcと、可視化用のarvizをインポートする。今回使ったpymc 5.7.2ではバックエンドでNumPyroによるMCMCを実行することができて、pymc3時代よりかなり速くなっているらしい。（NumPyroを使うからそのためにjaxが必要でCPUのプロセッサ数を指定していた）

import pymc as pm
import arviz as az
print('version.', pm.__version__)
# >> version. 5.7.2

# import numpyro
# print('version.', numpyro.__version__)
# >> version. 0.12.1

データ

まずはデータを作る。ChatGPTさんに手伝ってもらった。
1レコード1顧客と想定して、購入回数、購入金額、最終来店日からの日数の3種の購買行動データを生成。
性別、年齢、職業、結婚の有無の4種の属性データを生成。
職業は'Student', 'Professional', 'Homemaker', 'Other'の4パターン。
目的変数としては、未来の購買有無を想定。
未来の購買有無が購買行動から決定されるように各購買行動のパラメータを設定するが、属性によってパラメータは変動するようなデータとする。
例えば「女性で学生なら、購入回数のパラメータの絶対値は大きくなる」といったイメージ（ランダム効果）。
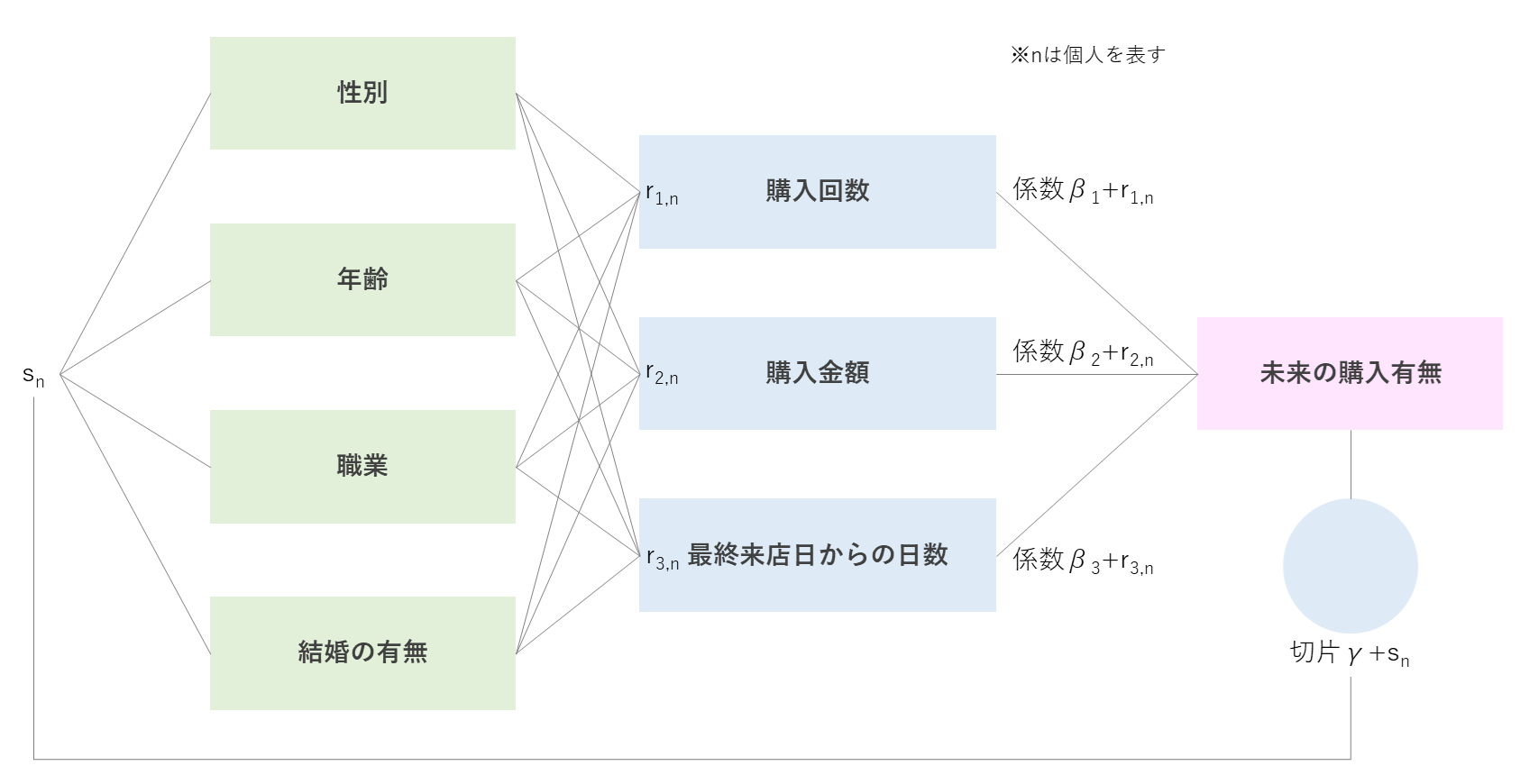
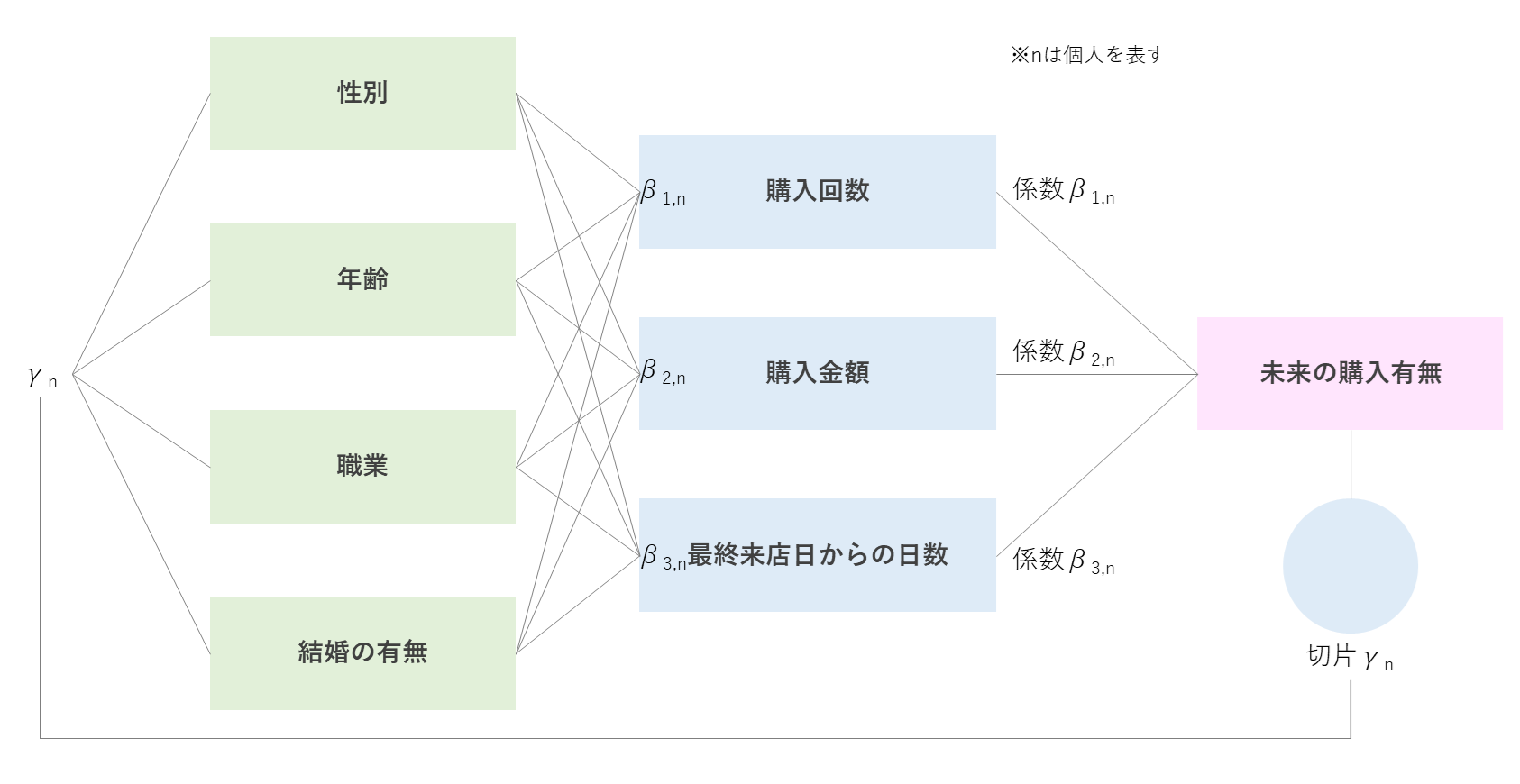
各変数の関係性としては以下図のような階層になっているイメージ。

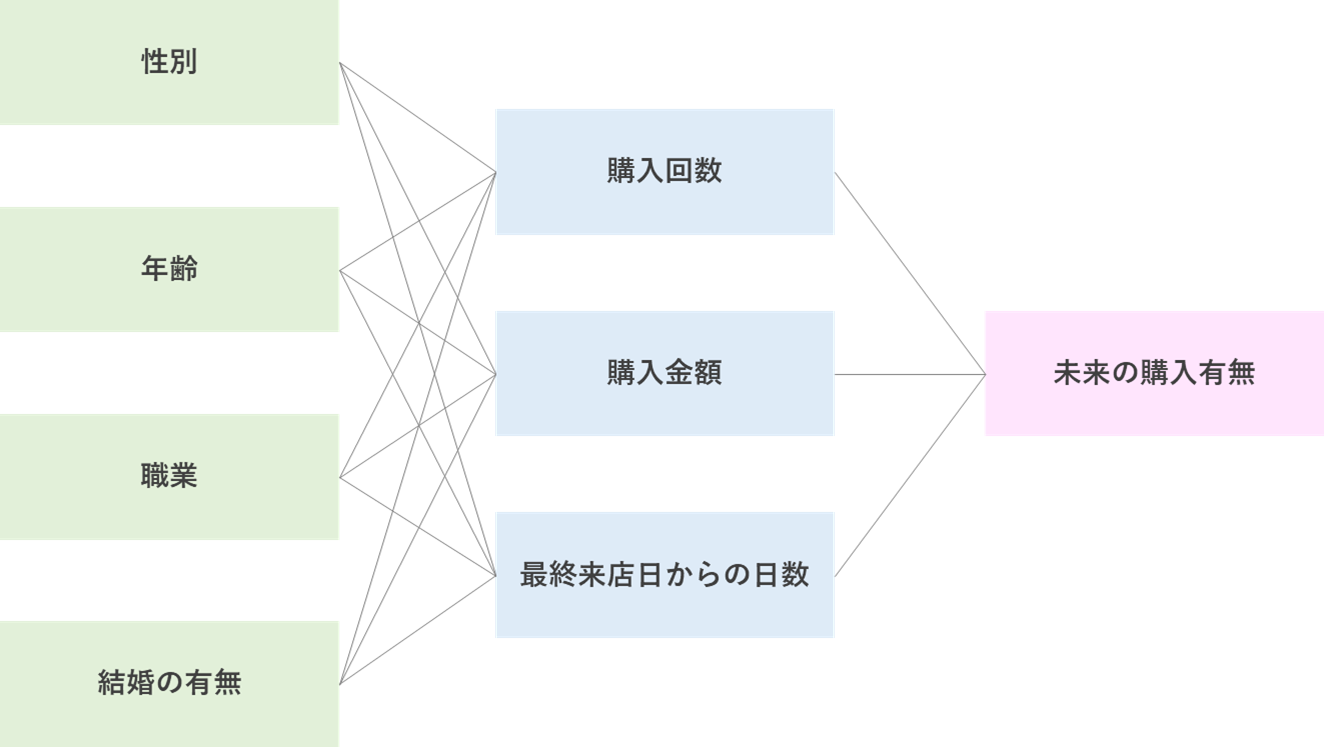
パラメータを決めたら、購買行動とパラメータから線形式を作って、シグモイド関数に突っ込んで確率として、0.5以上なら未来の購買ありとして目的変数とする。
サンプルサイズは2,000に設定したが、不均衡データにするために一部除外し最終的に1,100となっている。

今回の設定ではパラメータは以下のような変動があるように設定している。

• 女性と学生の場合購入回数のパラメータの絶対値が大きい
• 男性とProfessionalの場合購入金額のパラメータ絶対値が大きい
• 未婚と40代以上の場合最終来店日からの日数のパラメータ絶対値が大きい

変動が無い場合のベースの値（固定効果）を記録し忘れてしまった…。（ランダムで設定しちゃったので正確な値がわからなくなっちゃった）
でも推定した感じ、多分こんな感じ。↓

• 購入回数のパラメータ（固定効果）：1.15
• 購入金額のパラメータ（固定効果）：1.90
• 最終来店日からの日数のパラメータ（固定効果）：-1.70

これらがランダム効果で各個人ごとに上下する感じ。

make_data = False
if make_data:
    #### データ作成 ####
    # シード値を設定して乱数を固定化（再現性を確保）
    np.random.seed(42)
    
    # データの準備
    num_customers = 2000
    num_features_purchase = 3  # 購入回数、購入金額、最終来店日からの日数
    num_features_attributes = 4  # 性別、年齢、職業、結婚未婚
    
    # 説明変数の生成
    purchase_count = (np.random.randint(0, 20, size=num_customers))  # 購入回数
    purchase_amount = purchase_count*500 + np.random.normal(-3000, 3000, size=num_customers) + 5000  # 購入金額
    np.place(purchase_amount, purchase_amount < 0, 0)
    np.place(purchase_count, purchase_amount == 0, 0)
    days_since_last_visit = max(purchase_count*3) + purchase_count*-3 + np.random.normal(-20, 20, size=num_customers) + 30   # 最終来店日からの日数
    np.place(days_since_last_visit, days_since_last_visit < 0, 0)
    
    purchase_count = scipy.stats.zscore(purchase_count)
    purchase_amount = scipy.stats.zscore(purchase_amount)
    days_since_last_visit = scipy.stats.zscore(days_since_last_visit)
    
    X_purchase = np.concatenate([purchase_count.reshape(-1,1), purchase_amount.reshape(-1,1), days_since_last_visit.reshape(-1,1)], axis=1)
    
    # 属性情報の生成
    gender = np.random.choice(['Male', 'Female'], size=num_customers)  # 性別
    age = np.random.randint(18, 65, size=num_customers)  # 年齢
    occupation = np.random.choice(['Student', 'Professional', 'Homemaker', 'Other'], size=num_customers)  # 職業
    marital_status = np.random.choice(['Married', 'Single'], size=num_customers)  # 結婚未婚
    
    # 目的変数の生成
    # 購買データから購買有無への実際のパラメータ設定
    true_coefficients_purchase_count = np.random.uniform(0,2,size=(num_customers))
    true_coefficients_purchase_amount = np.random.uniform(0,2,size=(num_customers))
    true_coefficients_purchase_last_visit = np.random.uniform(-2,0,size=(num_customers))
    # 属性によってパラメータが大きくなる
    # 女性と学生の場合購入回数のパラメータが大きい(負の場合小さい)
    true_coefficients_purchase_count = [true_coefficients_purchase_count[i]*1.7 if gender[i] == 'Female' else true_coefficients_purchase_count[i] for i in range(num_customers)]
    true_coefficients_purchase_count = [true_coefficients_purchase_count[i]*1.6 if occupation[i] == 'Student' else true_coefficients_purchase_count[i] for i in range(num_customers)]
    # 男性とProfessionalの場合購入金額のパラメータが大きい(負の場合小さい)
    true_coefficients_purchase_amount = [true_coefficients_purchase_amount[i]*1.8 if gender[i] == 'Male' else true_coefficients_purchase_amount[i] for i in range(num_customers)]
    true_coefficients_purchase_amount = [true_coefficients_purchase_amount[i]*1.9 if occupation[i] == 'Professional' else true_coefficients_purchase_amount[i] for i in range(num_customers)]
    # 未婚と40代以上の場合最終来店日からの日数のパラメータが大きい(負の場合小さい)
    true_coefficients_purchase_last_visit = [true_coefficients_purchase_last_visit[i]*(1.5) if marital_status[i] == 'Single' else true_coefficients_purchase_last_visit[i] for i in range(num_customers)]
    true_coefficients_purchase_last_visit = [true_coefficients_purchase_last_visit[i]*(1.8) if age[i] >= 40 else true_coefficients_purchase_last_visit[i] for i in range(num_customers)]
    true_coefficients_purchase = np.vstack([true_coefficients_purchase_count, true_coefficients_purchase_amount, true_coefficients_purchase_last_visit]).T
    true_intercept_purchase = np.random.randn(1)[0]
    # 将来の購入有無
    # ノイズ
    noise_purchase = np.random.randn(num_customers)
    # 線形式
    purchase_behavior = true_intercept_purchase + np.sum(true_coefficients_purchase*X_purchase, axis=1) + noise_purchase
    # シグモイドで確率に
    purchase_probabilities = 1 / (1 + np.exp(-purchase_behavior))  # 購入確率
    purchase_events = np.round(purchase_probabilities)  # 購入有無

さて、各変数を作ったので、それらをデータフレームにまとめておく。 学習データとテストデータも分けておく。

if make_data:
    # 変数まとめ
    print('変数まとめ')
    # 各データを一つのdfにまとめる
    concatnp = np.concatenate([gender.reshape(-1,1), age.reshape(-1,1), occupation.reshape(-1,1), marital_status.reshape(-1,1), X_purchase, purchase_probabilities.reshape(-1,1), purchase_events.reshape(-1,1)], axis=1)
    democols = ['gender','age','occupation','marital_status']  # 属性のカラム名
    purchasecols = ['purchase_count','purchase_amount','last_visit']  # 購買行動のカラム名
    objectivecols = ['probabilities','purchase']  # 目的変数のカラム名
    # df作成
    train_df = pd.DataFrame(concatnp, columns=democols+purchasecols+objectivecols)
    # 前処理
    train_df[purchasecols+objectivecols] = train_df[purchasecols+objectivecols].astype(float)  # 型変更
    train_df['age'] = train_df['age'].astype(int)  # 型変更
    train_df = pd.get_dummies(train_df, columns=['occupation'])  # OneHotEncoding
    train_df = train_df.replace({'gender': {'Male': 1, 'Female': 0}, 'marital_status': {'Married': 1, 'Single':0}}) # binary
    democols = ['gender','age','marital_status', 'occupation_Homemaker', 'occupation_Other', 'occupation_Professional'] # Encoding後の属性カラム名
    train_df = train_df[democols+purchasecols+objectivecols]
    # 2値分類はなんだかんだ不均衡がほとんどなので不均衡にしておく
    imb_idx1 = train_df[train_df['purchase']==1].sample(int(num_customers*0.1)).index.to_list()  # 正例を全体の10%に減らしIndex取得
    imb_idx0 = train_df[train_df['purchase']==0].index.to_list()  # 負例のIndex取得
    train_df = train_df.loc[(imb_idx0+imb_idx1),:].reset_index(drop=True)  # 不均衡データにする
    print('All imbalanced', train_df.purchase.sum()/len(train_df))  # 不均衡 Ratio
    # train_test_split
    train_df, test_df = train_test_split(train_df, test_size=0.3333, shuffle=True, stratify=train_df['purchase'].to_numpy())
    print('Train imbalanced', train_df.purchase.sum()/len(train_df))  # 不均衡 Ratio
    print('Test imbalanced', test_df.purchase.sum()/len(test_df))  # 不均衡 Ratio
    # probabilitiesでソート
    train_df = train_df.sort_values('probabilities').reset_index(drop=True).reset_index()
    test_df = test_df.sort_values('probabilities').reset_index(drop=True).reset_index()
    display(train_df)
    display(test_df)
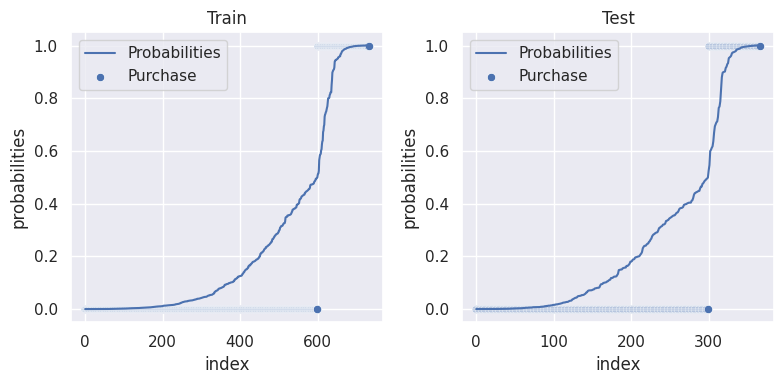
    # visualization
    fig, ax = plt.subplots(1,2,figsize=(8, 4))
    sns.lineplot(data=train_df, x='index', y='probabilities', ax=ax[0], label='Probabilities')
    sns.scatterplot(data=train_df, x='index', y='purchase', ax=ax[0], label='Purchase')
    sns.lineplot(data=test_df, x='index', y='probabilities', ax=ax[1], label='Probabilities')
    sns.scatterplot(data=test_df, x='index', y='purchase', ax=ax[1], label='Purchase')
    ax[0].set_title("Train")
    ax[1].set_title("Test")
    plt.tight_layout()
    plt.show()

    # 保存
    train_df.to_csv('train_df.csv', index=False)
    test_df.to_csv('test_df.csv', index=False)

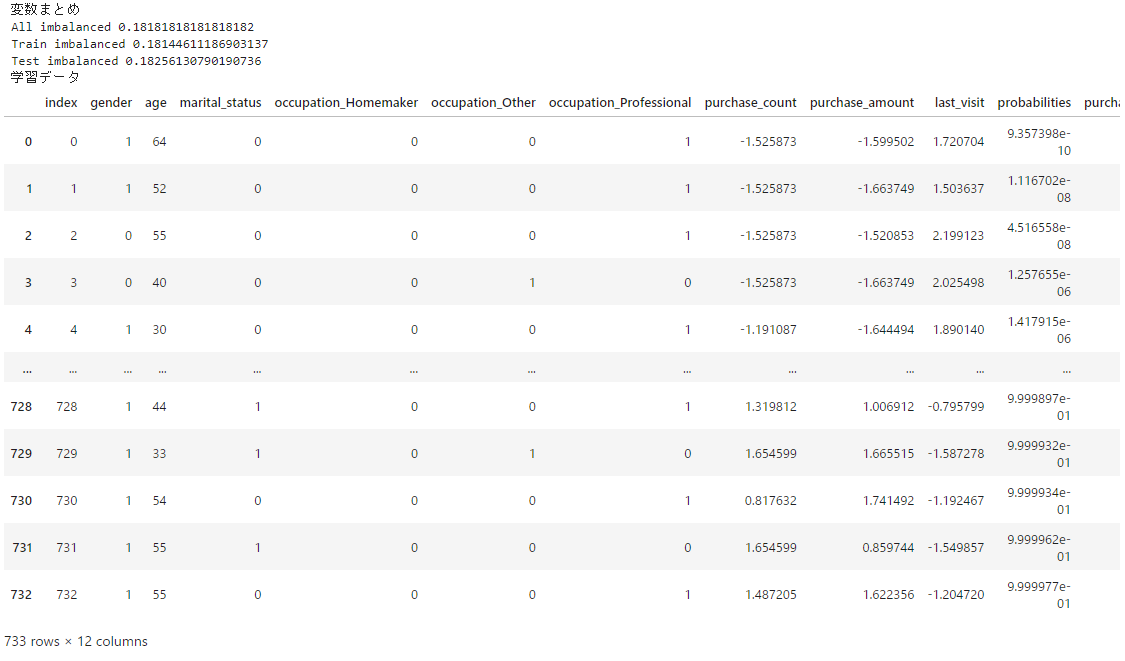
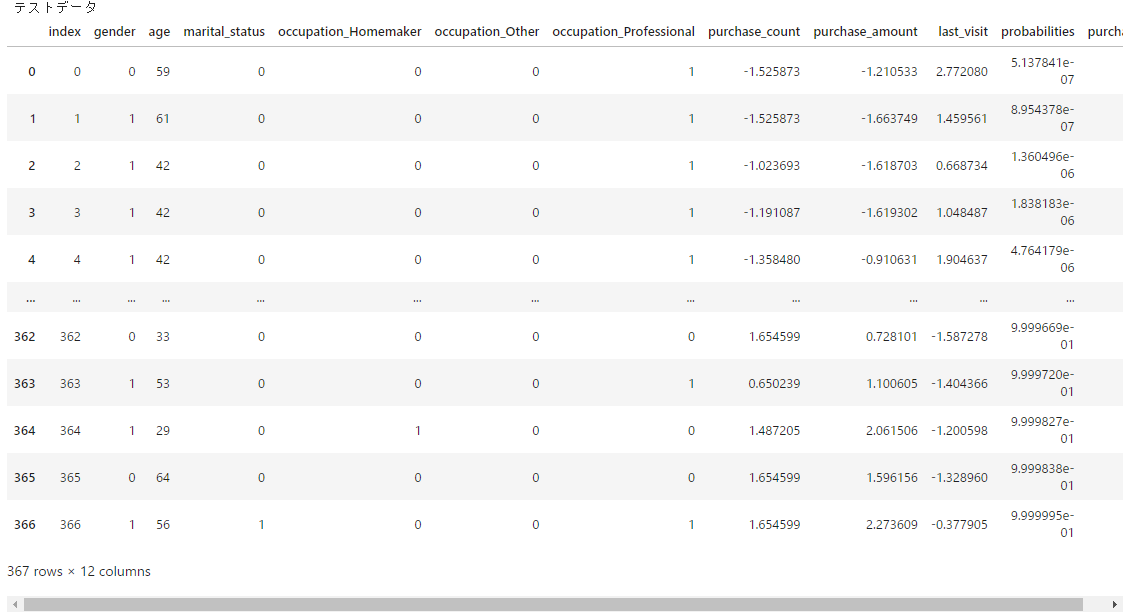
（各個人の実際の購入確率を昇順に並べてプロットしているだけ。0.5未満は0、0.5以上は1として散布図も書いている。）

※1度作ったデータを呼び出すときは以下のコード。

# 保存したものを読み込む
democols = ['gender','age','marital_status', 'occupation_Homemaker', 'occupation_Other', 'occupation_Professional']
purchasecols = ['purchase_count','purchase_amount','last_visit']
objectivecols = ['probabilities','purchase']
train_df = pd.read_csv('train_df.csv')
test_df = pd.read_csv('test_df.csv')
display('Train', train_df.head())
display('Test', test_df.head())
print('Train imbalanced', train_df.purchase.sum()/len(train_df))  # 不均衡 Ratio
print('Test imbalanced', test_df.purchase.sum()/len(test_df))  # 不均衡 Ratio
# visualization
fig, ax = plt.subplots(1,2,figsize=(8, 4))
sns.lineplot(data=train_df, x='index', y='probabilities', ax=ax[0], label='Probabilities')
sns.scatterplot(data=train_df, x='index', y='purchase', ax=ax[0], label='Purchase')
sns.lineplot(data=test_df, x='index', y='probabilities', ax=ax[1], label='Probabilities')
sns.scatterplot(data=test_df, x='index', y='purchase', ax=ax[1], label='Purchase')
ax[0].set_title("Train")
ax[1].set_title("Test")
plt.tight_layout()
plt.show()

関数定義

結果評価用の関数群を定義しておく。分類指標とか混同行列とか、推定したパラメータ可視化したりとかする関数いろいろ。本題ではないので詳細は書かない。

関数定義部分

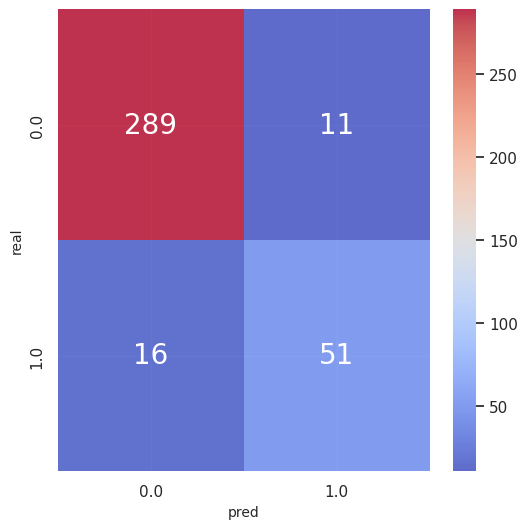
# 混同行列
def print_cmx(y_true, y_pred):
    '''create confusion matrix
    y_true:True data
    y_pred:Pred data
    '''
    labels = sorted(list(set(y_true)))
    cmx_data = confusion_matrix(y_true, y_pred, labels=labels)

    df_cmx = pd.DataFrame(cmx_data, index=labels, columns=labels)

    plt.figure(figsize = (6,6))
    sns.heatmap(df_cmx, annot=True, fmt='d', cmap='coolwarm', annot_kws={'fontsize':20},alpha=0.8)
    plt.xlabel('pred', fontsize=10)
    plt.ylabel('real', fontsize=10)
    plt.show()

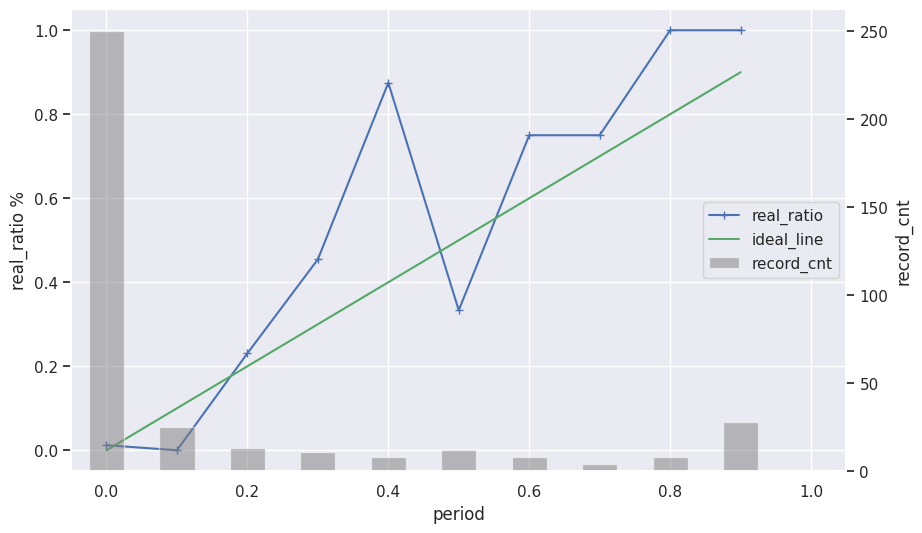
# 予測確率－実測確率曲線を返す=Calibration Curve
def calib_curve(y_tests, y_pred_probas, xlim=[-0.05,1.05], ylim=[-0.05,1.05]):
    # 実測値入れる
    proba_check=pd.DataFrame(y_tests,columns=['real'])
    # 予測確率値入れる
    proba_check['pred']=y_pred_probas
    # 予測確率値10%刻み
    s_cut, bins = pd.cut(proba_check['pred'], list(np.linspace(0,1,11)), right=False, retbins=True)
    labels=bins[:-1]
    s_cut = pd.cut(proba_check['pred'], list(np.linspace(0,1,11)), right=False, labels=labels)
    proba_check['period']=s_cut.values
    # 予測確率値10%ごとの実際の確率とレコード数集計
    proba_check = pd.merge(proba_check.groupby(['period'])[['real']].mean().reset_index().rename(columns={'real':'real_ratio'})\
                            , proba_check.groupby(['period'])[['real']].count().reset_index().rename(columns={'real':'record_cnt'})\
                            , on=['period'], how='left')
    proba_check['period']=proba_check['period'].astype(str)
    proba_check['period']=proba_check['period'].astype(float)
    fig=plt.figure(figsize=(10,6))
    ax1 = plt.subplot(1,1,1)
    ax2=ax1.twinx()
    ax2.bar(proba_check['period'].values, proba_check['record_cnt'].values, color='gray', label="record_cnt", width=0.05, alpha=0.5)
    ax1.plot(proba_check['period'].values, proba_check['real_ratio'].values, color=sns.color_palette()[0],marker='+', label="real_ratio")
    ax1.plot(proba_check['period'].values, proba_check['period'].values, color=sns.color_palette()[2], label="ideal_line")
    handler1, label1 = ax1.get_legend_handles_labels()
    handler2, label2 = ax2.get_legend_handles_labels()
    ax1.legend(handler1 + handler2, label1 + label2, loc='center right')
    ax1.set_xlim(xlim[0],xlim[1])
    ax1.set_ylim(ylim[0],ylim[1])
    ax1.set_xlabel('period')
    ax1.set_ylabel('real_ratio %')
    ax2.set_ylabel('record_cnt')
    ax2.grid(False)
    plt.show()
    display(proba_check)

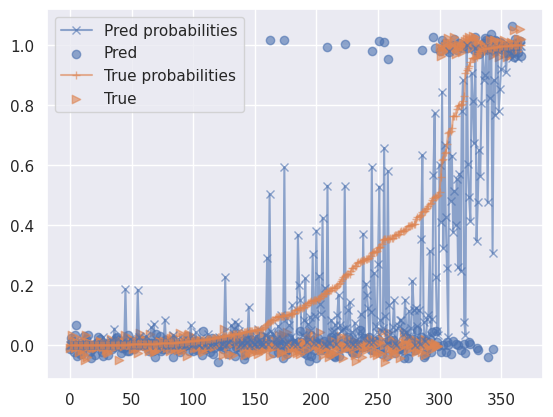
# 実際の確率と予測確率の比較
def probabilities_compare(p_true, p_pred, y_true, y_pred):
    idx = np.argsort(p_true)
    plt.plot(range(len(p_pred)), p_pred[idx], label='Pred probabilities', marker='x', alpha=0.6)
    plt.scatter(range(len(p_pred)), np.random.normal(y_pred[idx], 0.02), marker='o', label='Pred', alpha=0.6)
    plt.plot(range(len(p_pred)), p_true[idx], label='True probabilities', marker='+', alpha=0.6)
    plt.scatter(range(len(p_pred)), np.random.normal(y_true[idx], 0.02), marker='>', label='True', alpha=0.6)
    plt.legend()
    plt.show()

# 分類指標、混同行列、予測確率-実測確率プロット(キャリブレーションカーブ)を出力
def result_summary(p_true, p_pred, y_true, y_pred):
    print('accuracy_score', sklearn.metrics.accuracy_score(y_true, y_pred))
    print('precision_score', sklearn.metrics.precision_score(y_true, y_pred))
    print('recall_score', sklearn.metrics.recall_score(y_true, y_pred))
    print('f1_score', sklearn.metrics.f1_score(y_true, y_pred))
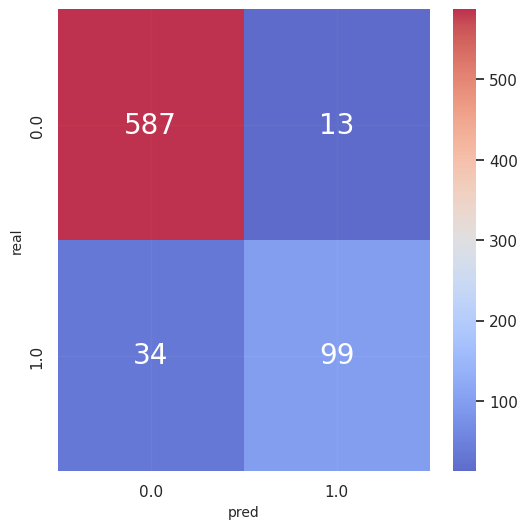
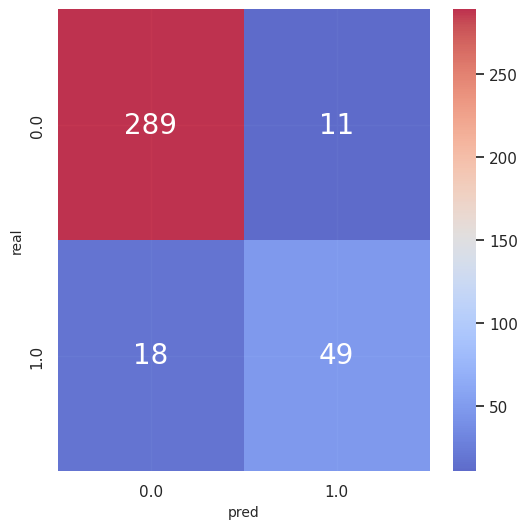
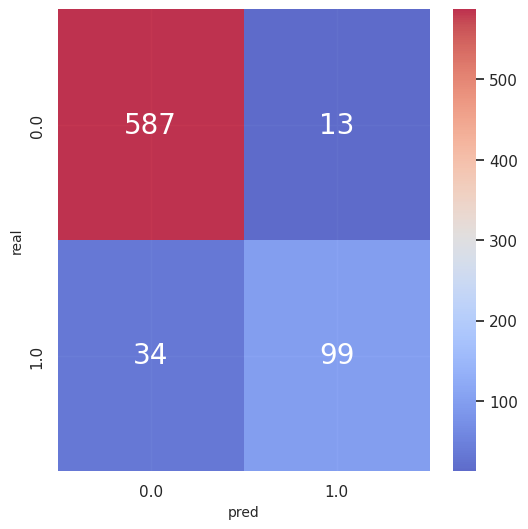
    print_cmx(y_true, y_pred)
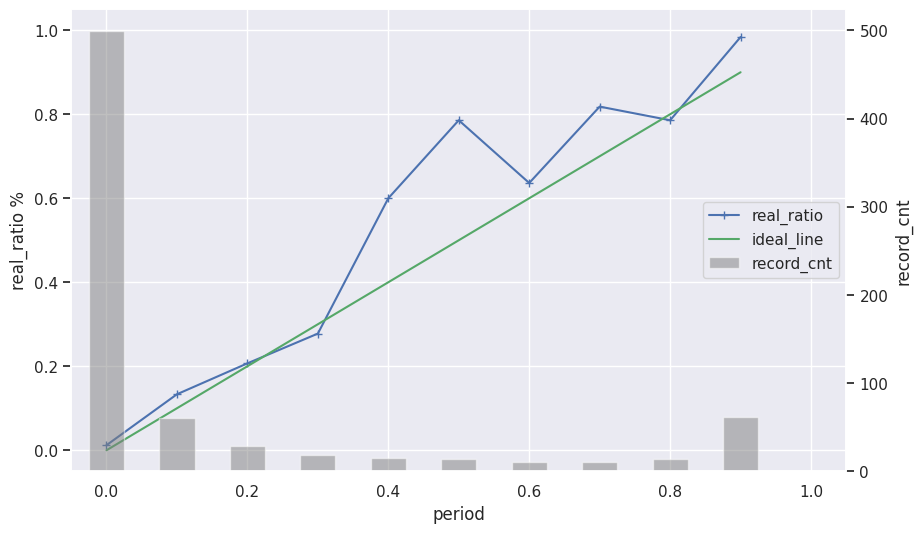
    calib_curve(y_true, p_pred, xlim=[-0.05,1.05], ylim=[-0.05,1.05])
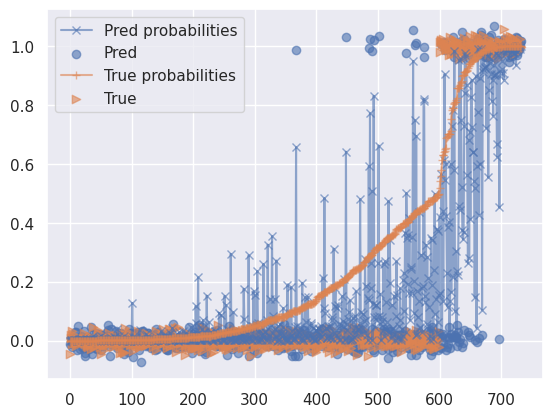
    probabilities_compare(p_true, p_pred, y_true, y_pred)

# バイオリンプロット
def plot_violin(data, order=None, xlabel=None, ylabel=None, title=None, figsize=(10,4)):
    fig=plt.figure(figsize=figsize)
    ax1 = plt.subplot(1,1,1)
    sns.violinplot(data=data, ax=ax1, order=order, scale='width')
    plt.setp(ax1.get_xticklabels(), rotation=20)
    for i, col in enumerate(corf_df.columns):
        ax1.text(i, corf_df[col].mean(), round(corf_df[col].mean(),2), fontsize=10, ha="left", color="k")
    ax1.set_xlabel(xlabel)
    ax1.set_ylabel(ylabel)
    ax1.set_title(title)
    plt.rcParams['font.family'] = prop.get_name()
    #plt.tight_layout()
    plt.show()

# 各個人のランダム係数効果計算
def random_coef_effect(trace, name):
    indivisual_coef_purchase_samples = trace.posterior[name].mean(dim=["chain"]).values
    indivisual_coef_purchase_samples_count = pd.DataFrame(indivisual_coef_purchase_samples[:, :, 0])
    indivisual_coef_purchase_samples_amount = pd.DataFrame(indivisual_coef_purchase_samples[:, :, 1])
    indivisual_coef_purchase_samples_last_visit = pd.DataFrame(indivisual_coef_purchase_samples[:, :, 2])
    return indivisual_coef_purchase_samples_count, indivisual_coef_purchase_samples_amount, indivisual_coef_purchase_samples_last_visit
    
# 個人単位のランダム係数のboxplot
def indivisual_plot(indivisual_coef, ylabel=None, title=None, brk=True):
    for i in (range(100, indivisual_coef.shape[1]+100, 100)):
        fig=plt.figure(figsize=(30,6))
        ax1 = plt.subplot(1,1,1)
        sns.boxplot(data=indivisual_coef.iloc[:,i-100:i], ax=ax1)
        plt.setp(ax1.get_xticklabels(), rotation=90)
        ax1.set_ylabel(ylabel)
        ax1.set_title(title)
        plt.rcParams['font.family'] = prop.get_name()
        #plt.tight_layout()
        plt.show()
        if brk:
            break

# 3種の属性グループのランダム係数のviolin plot
def indivisual_summary_plot(train_df, democols, indivisual_count, indivisual_amount, indivisual_last_visit):
    DfForPlot = train_df[democols].copy()
    DfForPlot['coef_count'] = indivisual_count.mean(axis=0)
    DfForPlot['coef_amount'] = indivisual_amount.mean(axis=0)
    DfForPlot['coef_last_visit'] = indivisual_last_visit.mean(axis=0)
    case1 = DfForPlot[(DfForPlot['gender']==0)&(DfForPlot['occupation_Homemaker']==0)&(DfForPlot['occupation_Other']==0)&(DfForPlot['occupation_Professional']==0)]
    case2 = DfForPlot[(DfForPlot['gender']==1)&(DfForPlot['occupation_Homemaker']==0)&(DfForPlot['occupation_Other']==0)&(DfForPlot['occupation_Professional']==1)]
    case3 = DfForPlot[(DfForPlot['age']>=40)&(DfForPlot['marital_status']==0)]
    length = max(len(case1),len(case2),len(case3))

    caseAll = pd.DataFrame()
    caseAll['coef_count1'] = np.pad(case1['coef_count'].to_numpy(),(0,length-len(case1['coef_count'].to_numpy())), mode='constant', constant_values=np.nan)
    caseAll['coef_count2'] = np.pad(case2['coef_count'].to_numpy(),(0,length-len(case2['coef_count'].to_numpy())), mode='constant', constant_values=np.nan)
    caseAll['coef_count3'] = np.pad(case3['coef_count'].to_numpy(),(0,length-len(case3['coef_count'].to_numpy())), mode='constant', constant_values=np.nan)
    fig=plt.figure(figsize=(6,10))
    ax1 = plt.subplot(3,1,1)
    sns.violinplot(data=caseAll, ax=ax1, order=['coef_count1','coef_count2','coef_count3'])
    plt.setp(ax1.get_xticklabels(), rotation=20)
    ax1.set_ylabel('購入回数の係数')
    ax1.set_title('"購入回数"の係数が各個人の属性情報によってばらつくことをモデル化')
    
    caseAll = pd.DataFrame()
    caseAll['coef_amount1'] = np.pad(case1['coef_amount'].to_numpy(),(0,length-len(case1['coef_amount'].to_numpy())), mode='constant', constant_values=np.nan)
    caseAll['coef_amount2'] = np.pad(case2['coef_amount'].to_numpy(),(0,length-len(case2['coef_amount'].to_numpy())), mode='constant', constant_values=np.nan)
    caseAll['coef_amount3'] = np.pad(case3['coef_amount'].to_numpy(),(0,length-len(case3['coef_amount'].to_numpy())), mode='constant', constant_values=np.nan)
    ax1 = plt.subplot(3,1,2)
    sns.violinplot(data=caseAll, ax=ax1, order=['coef_amount1','coef_amount2','coef_amount3'])
    plt.setp(ax1.get_xticklabels(), rotation=20)
    ax1.set_ylabel('購入金額の係数')
    ax1.set_title('"購入金額"の係数が各個人の属性情報によってばらつくことをモデル化')
    
    caseAll = pd.DataFrame()
    caseAll['coef_last_visit1'] = np.pad(case1['coef_last_visit'].to_numpy(),(0,length-len(case1['coef_last_visit'].to_numpy())), mode='constant', constant_values=np.nan)
    caseAll['coef_last_visit2'] = np.pad(case2['coef_last_visit'].to_numpy(),(0,length-len(case2['coef_last_visit'].to_numpy())), mode='constant', constant_values=np.nan)
    caseAll['coef_last_visit3'] = np.pad(case3['coef_last_visit'].to_numpy(),(0,length-len(case3['coef_last_visit'].to_numpy())), mode='constant', constant_values=np.nan)
    ax1 = plt.subplot(3,1,3)
    sns.violinplot(data=caseAll, ax=ax1, order=['coef_last_visit1','coef_last_visit2','coef_last_visit3'])
    plt.setp(ax1.get_xticklabels(), rotation=20)
    ax1.set_ylabel('最終来店からの日数の係数')
    ax1.set_title('"最終来店からの日数"の係数が各個人の属性情報によってばらつくことをモデル化')
    plt.rcParams['font.family'] = prop.get_name()
    plt.tight_layout()
    plt.show()

scikit-learnロジスティック回帰モデル

まず、ベイズモデリングではなく、scikit-learnでロジスティック回帰モデルを構築してみる。購買行動と属性情報のどちらも説明変数に加えてモデルを構築。
ちゃちゃっと学習から出力までドン。↓

# 学習データ、テストデータ定義
# 説明変数は購買行動と属性情報
X_train = train_df[democols+purchasecols]
y_train = train_df['purchase']
X_test = test_df[democols+purchasecols]

# モデルの初期化
modellr = LogisticRegression()

# モデルのトレーニング
modellr.fit(X_train, y_train)

coef_dict = {i:round(j,2) for i,j in zip(democols+purchasecols, modellr.coef_[0])}
print('coef_', coef_dict)
# 学習データを使って予測
p_pred = modellr.predict_proba(X_train)[:,1]
y_pred = (p_pred >= 0.5).astype("int")  # 0.5以上を1
y_true = train_df['purchase'].to_numpy()  # 実際の購買有無
p_true = train_df['probabilities'].to_numpy()
result_summary(p_true, p_pred, y_true, y_pred)

# テストデータを使って予測
p_pred_test = modellr.predict_proba(X_test)[:,1]
y_pred_test = (p_pred_test >= 0.5).astype("int")  # 0.5以上を1
y_true_test = test_df['purchase'].to_numpy()  # 実際の購買有無
p_true_test = test_df['probabilities'].to_numpy()
result_summary(p_true_test, p_pred_test, y_true_test, y_pred_test)

学習データの推論結果、テストデータの推論結果どちらも出している。
テストデータf1_score 0.77と、まあぼちぼちの結果。予測の性能はこれをベースとする。

• 各説明変数の偏回帰係数
  >> coef_ {'gender': -0.03, 'age': 0.0, 'marital_status': 0.19, 'occupation_Homemaker': 0.02, 'occupation_Other': -0.35, 'occupation_Professional': -0.22, 'purchase_count': 1.13, 'purchase_amount': 1.86, 'last_visit': -1.68}

• 評価指標（学習データ）
  accuracy_score 0.9358799454297408
precision_score 0.8839285714285714
recall_score 0.7443609022556391
f1_score 0.8081632653061225

• 混同行列（学習データ）
  

• キャリブレーションカーブ（学習データ）
  

• データ作成時の実際の確率と予測確率のプロット（1,0の散布図は少しばらけさせている）（学習データ）
  

• 評価指標（テストデータ）
  accuracy_score 0.9209809264305178
precision_score 0.8166666666666667
recall_score 0.7313432835820896
f1_score 0.7716535433070867

• 混同行列（テストデータ）
  

• キャリブレーションカーブ（テストデータ）
  

• データ作成時の実際の確率と予測確率のプロット(1,0の散布図は少しばらけさせている)（テストデータ）
  

ベイズロジスティック回帰モデル

次、ベイズモデリングのアプローチでロジスティック回帰モデルを構築してみる。購買行動と属性情報のどちらも説明変数に加えてモデルを構築する。

モデルの定義

まずpymcでモデルを定義していく。
説明変数を"x"、目的変数を"y"と定義し、推定する各係数と切片（"coef", "intercept"）は正規分布を事前分布としている。各係数と切片による線形モデルを"mu"と定義し、逆リンク関数はシグモイド関数、出力の分布はベルヌーイ分布とするようなモデルを想定。

# モデルの定義
with pm.Model() as model_logi:
    # coords(次元やインデックスを定義)
    model_logi.add_coord('data', values=range(train_df.shape[0]), mutable=True)
    model_logi.add_coord('var', values=democols+purchasecols, mutable=True)

    # 説明変数
    x = pm.MutableData('x', train_df[democols+purchasecols].to_numpy(), dims=('data', 'var'))
    y = pm.MutableData("y", train_df['purchase'].to_numpy(), dims=('data', ))

    # 推論パラメータの事前分布
    coef_ = pm.Normal('coef', mu=0.0, sigma=1, dims="var")  # 各係数の事前分布は正規分布
    intercept_ = pm.Normal('intercept', mu=0.0, sigma=1.0)  # 切片の事前分布は正規分布
    # linear model
    mu = pm.Deterministic("mu", coef_.dot(x.T) + intercept_, dims=('data', ))
    # link function
    link = pm.Deterministic("link", pm.math.invlogit(mu), dims=('data', ))
    # likelihood
    result = pm.Bernoulli("obs", p=link, observed=y, dims=('data', ))

# 定義した各パラメータの情報
display(model_logi.model)

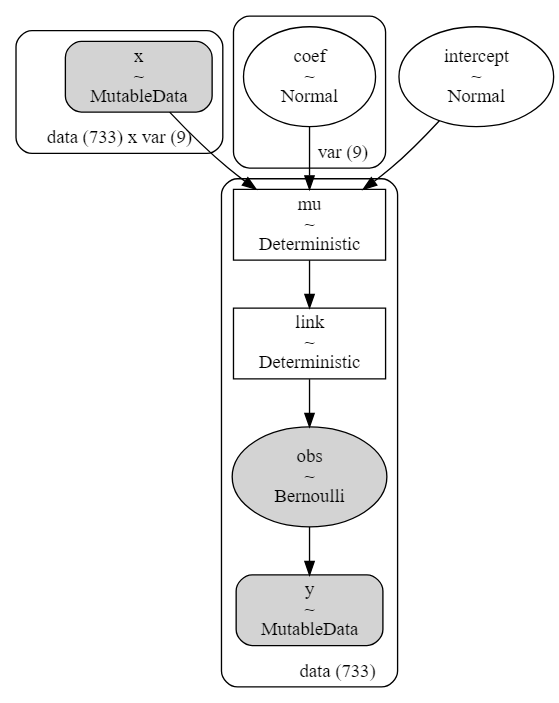
モデルの構造も可視化できる。"x"と係数と切片によって"mu"の線形モデルができ、"mu"に逆リンク関数が適用され、ベルヌーイ分布の出力を得る。

# モデル構造
modeldag = pm.model_to_graphviz(model_logi)
display(modeldag)

MCMC

係数や切片パラメータの事後分布は解析解が導出できないのでMCMCで推定する。引数nuts_samplerのNUTSってのはMCMCのためのサンプリングアルゴリズム。いやー難しくてよくわからん。MCMCにフォーカスされた書籍も買わないとな…。nuts_sampler="numpyro"とすることでバックエンドではnumpyroを使ってくれる。サンプルサイズは3000で最初の1000は捨て、チェーン数は3としている。

%%time
# MCMC実行
# バックエンドでNumPyroで実行
with model_logi:
    # MCMCによる推論
    trace = pm.sample(draws=3000, tune=1000, chains=3, nuts_sampler="numpyro", random_seed=1, return_inferencedata=True)
# >> Wall time: 7.58 s

MCMCの収束を評価する。トレースプロットや$\hat{R}$と呼ばれる統計量を見ることで収束の判断をする。$\hat{R}$は各チェーン内の分散とチェーン間の分散を比較した指標で、1に近いほど好ましく、基本的に1.1以下なら良いとされているそう。
今回のベイズロジスティック回帰のMCMCでは最大の$\hat{R}$は1.00だったので収束は問題なさそう。

# MCMCの収束を評価
rhat_vals = az.rhat(trace).values()
# 最大のRhatを確認
result = np.max([np.max(i.values) for i in rhat_vals if i.name in ["coef", "intercept"]])
print('Max rhat:', result)
# 1.1以上のRhatを確認
for i in rhat_vals:
    if np.max(i.values)>=1.1:
        print(i.name, np.max(i.values), np.mean(i.values), i.values.shape, sep='  ====>  ')
# >>Max rhat: 1.0010951683443083

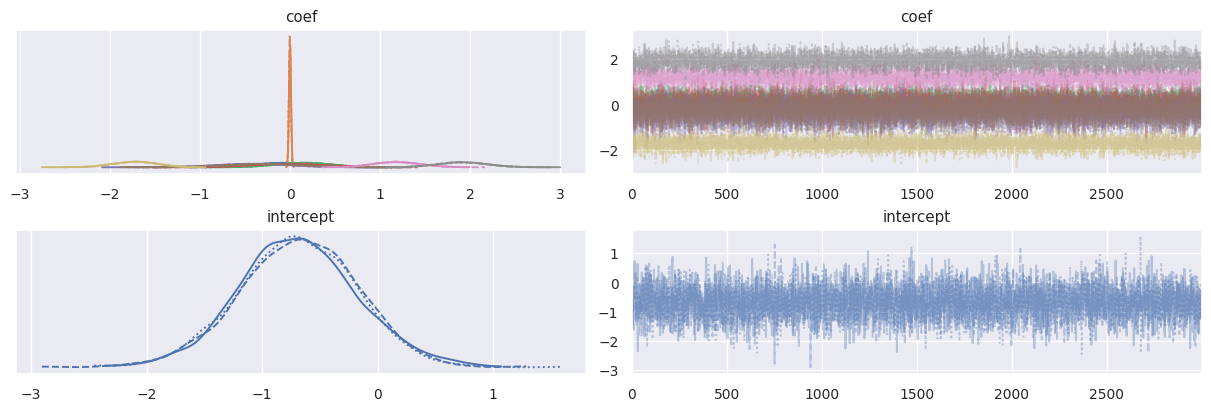
plot_traceでトレースプロットも見ておく。
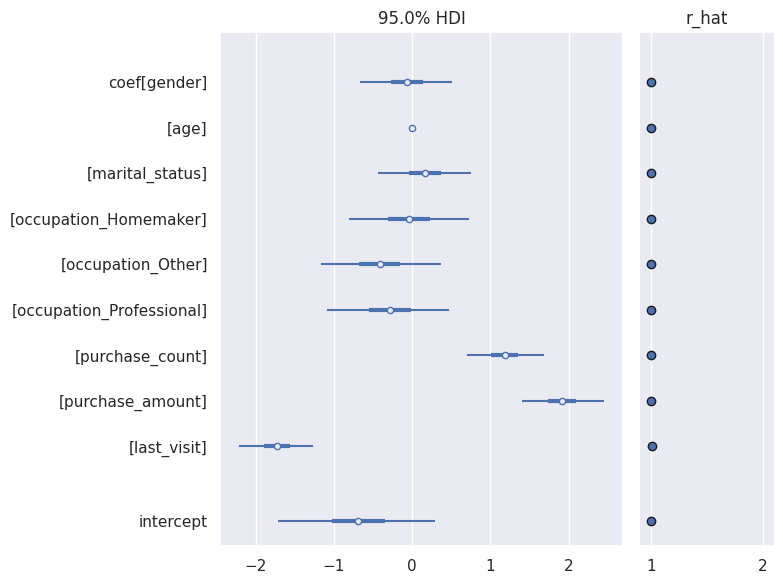
またplot_forestで$\hat{R}$と一緒に可視化もできる。
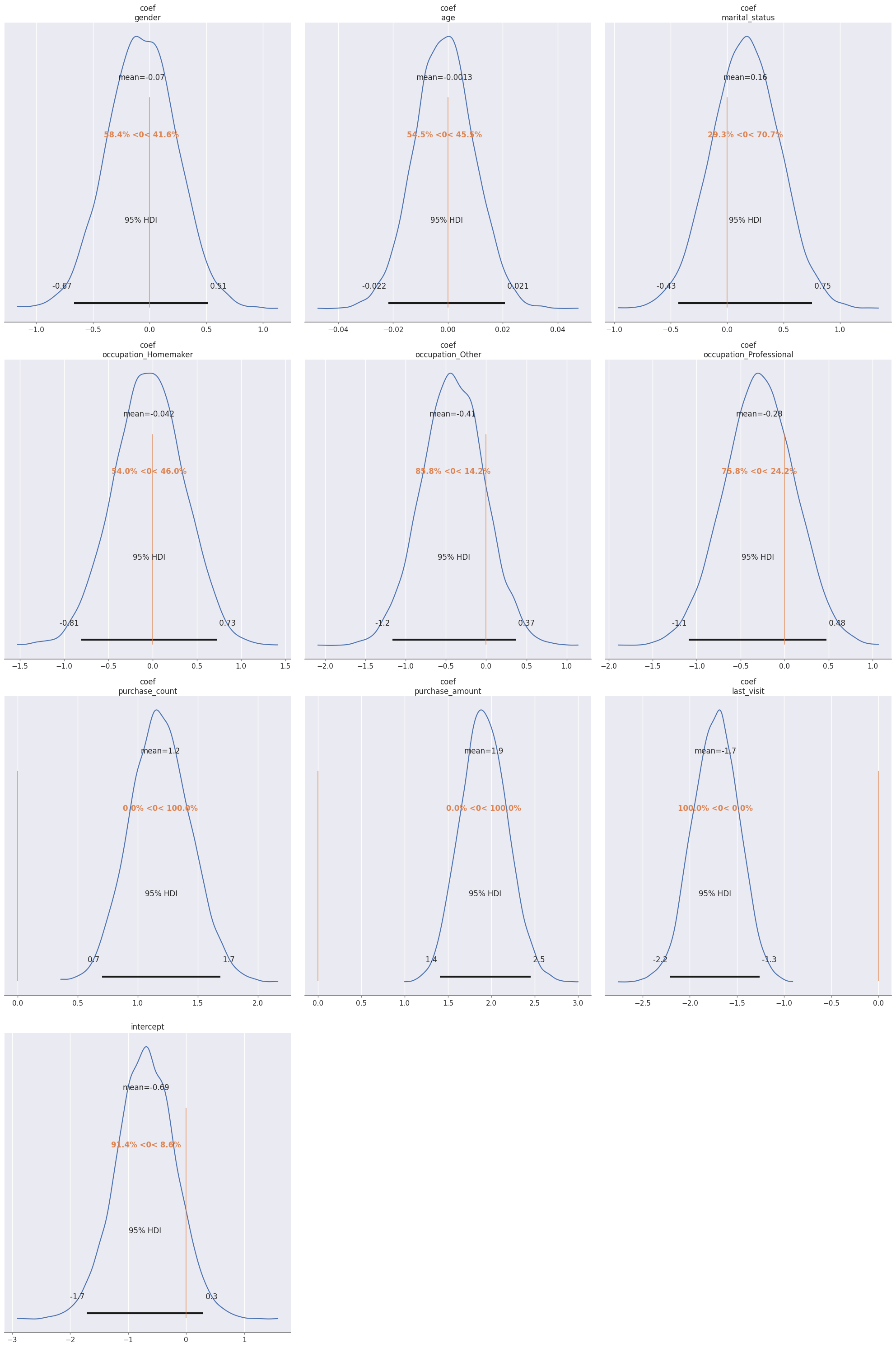
各パラメータの事後分布はplot_posteriorで確認できる。

# plot_trace
az.plot_trace(trace, backend_kwargs={"constrained_layout":True}, var_names=["coef", "intercept"])
plt.show()

# forest plotでRハットと一緒に可視化
az.plot_forest(trace, combined=True, hdi_prob=0.95, r_hat=True, var_names=["coef", "intercept"])
plt.tight_layout()
plt.show()

# 事後分布の確認
az.plot_posterior(trace, hdi_prob=0.95, var_names=["coef", "intercept"], ref_val=0, figsize=(20,30))
plt.tight_layout()
plt.show()

plot_trace

plot_forest

plot_posterior

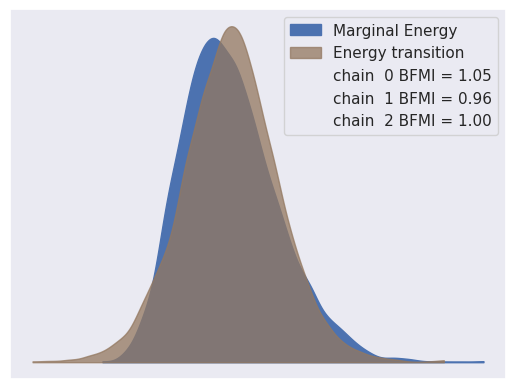
よく理解できていないのだが、Energy Plotというものでもサンプリングの評価ができる。「PyMC：重回帰を題材にしたPyMCの紹介」によると、

理想的なプロットとしてはMarginal EnergyとEnergy Transitionの分布が一致していることです。一致していればHMCやNUTSは目的としている分布をよくサンプリングできていることを意味しています。逆に、左下図のようにEnergy Transition分布の方がMarginal Energyの分布より狭い場合、HMCやNUTSは目的としている領域の一部しかサンプリングできておらいないことを意味しています。このような場合はNealの漏斗のようなサンプリングが難しくなってしまっているので、再パラメータ化やモデルを単純化するなどでサンプリングがうまくいくように変更が必要です。
参考：https://arxiv.org/pdf/1701.02434.pdf のfig 23,34

とのこと。なるほどわからん。

az.plot_energy(trace)
plt.show()

予測サンプル生成（学習データ）

特に意味は無いが、学習データの予測結果をまず見てみる。sample_posterior_predictiveで事後分布から予測サンプルを生成する。

# 事後分布から予測サンプルを生成
with model_logi:
    idata = pm.sample_posterior_predictive(trace)

# 学習データを使って予測
p_preds = idata.posterior_predictive['obs'].mean(dim=["chain"]).values  # chain平均
p_pred = idata.posterior_predictive['obs'].mean(dim=["chain", "draw"]).values  # chainとサンプル平均
y_pred = (p_pred >= 0.5).astype("int")  # 0.5以上を1
y_true = train_df['purchase'].to_numpy()  # 実際の購買有無
p_true = train_df['probabilities'].to_numpy()
result_summary(p_true, p_pred, y_true, y_pred)

• 評価指標（学習データ）
  accuracy_score 0.9358799454297408
precision_score 0.8839285714285714
recall_score 0.7443609022556391
f1_score 0.8081632653061225

• 混同行列（学習データ）
  
  （他指標は省略）

推定パラメータ確認

推定した係数、切片パラメータの平均と、分布を確認する。
完全に一致しているわけではないが、scikit-learnで求めたパラメータと近いものが求まっている。scikit-learnによる結果と違って、推定したパラメータの分布が見られるのもベイズモデリングの良いところ。

corf_df = pd.DataFrame(trace.posterior['coef'].mean(dim=["chain"]).values, columns=democols+purchasecols)
coef_dict = {i:round(corf_df[i].mean(),2) for i in democols+purchasecols}
print(coef_dict)
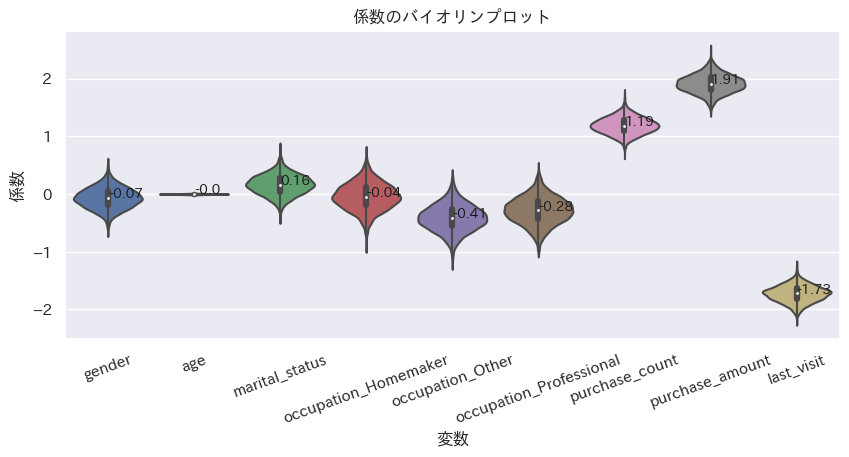
plot_violin(corf_df, order=None, xlabel='変数', ylabel='係数', title='係数のバイオリンプロット')

• 各説明変数の偏回帰係数サンプルの平均
  >> coef {'gender': -0.07, 'age': -0.0, 'marital_status': 0.16, 'occupation_Homemaker': -0.04, 'occupation_Other': -0.41, 'occupation_Professional': -0.28, 'purchase_count': 1.19, 'purchase_amount': 1.91, 'last_visit': -1.73}
• 各説明変数の偏回帰係数サンプルの分布
  

予測サンプル生成（テストデータ）

未知のデータに対しても予測結果は返せる。
pm.set_dataでテストデータの情報に更新した後に、pm.sample_posterior_predictive()で予測を行う。

# テストデータの推論
with model_logi:
    pm.set_data({'x':test_df[democols+purchasecols].to_numpy()
                 , 'y': np.zeros(len(test_df[democols+purchasecols].to_numpy()))  # yは未知とする。実際の答えはtest_df['purchase'].to_numpy()。
                }
                , coords={"data": (np.arange(test_df.shape[0]))+train_df.shape[0]}
               )
    trace.extend(pm.sample_posterior_predictive(trace))

テストデータはf1_score 0.79と、まあぼちぼちの結果。scikit-learnの結果よりはちょっとだけ良かった。

# テストデータを使って予測
p_preds_test = trace.posterior_predictive["obs"].mean(dim=["chain"]).values  # chain平均
p_pred_test = trace.posterior_predictive["obs"].mean(dim=["chain", "draw"]).values  # chainとサンプル平均
y_pred_test = (p_pred_test >= 0.5).astype("int")  # 0.5以上を1
y_true_test = test_df['purchase'].to_numpy()  # 実際の購買有無
p_true_test = test_df['probabilities'].to_numpy()
result_summary(p_true_test, p_pred_test, y_true_test, y_pred_test)

• 評価指標（テストデータ）
  accuracy_score 0.9264305177111717
precision_score 0.8225806451612904
recall_score 0.7611940298507462
f1_score 0.7906976744186047

• 混同行列（テストデータ）
  
  （他指標は省略）

階層ベイズ二項ロジットモデル: 属性情報なし 固定効果あり ランダム効果あり

ここからようやく階層ベイズモデリングへ。
まず最初に、属性情報を使わない階層ベイズモデルを作ってみる。
購買行動と将来の購入有無の関係性をモデリングするので各購買行動の係数パラメータを推定するのだが、階層ベイズでは各個人によってその係数パラメータがランダム効果によって上下するようなイメージ。
係数$β_{i}$と切片$γ$を用いてロジスティック回帰モデルを数式で表すと、説明変数が3つなのでランダム効果が無い場合以下のような式になるが、

\log (\frac{p}{1-p})=β_{1}x_{1}+β_{2}x_{2}+β_{3}x_{3}+γ

β_{i} \sim \mathcal{N}(μ_{c},\sigma_{c}^2)

γ \sim \mathcal{N}(μ_{d},\sigma_{d}^2)

個人ごとのランダム係数$r_{i,n}$、ランダム切片$s_{n}$（$n$は各個人）がある場合以下のような式になる。

\log (\frac{p}{1-p})=(β_{1}+r_{1,n})x_{1}+(β_{2}+r_{2,n})x_{2}+(β_{3}+r_{3,n})x_{3}+γ+s_{n}

μ_{r_{i,n}} \sim \mathcal{N}(μ_{a},\sigma_{a}^2)

μ_{s_{n}} \sim \mathcal{N}(μ_{b},\sigma_{b}^2)

r_{i,n} \sim \mathcal{N}(μ_{r_{i,n}},\sigma_{1}^2)

s_{n} \sim \mathcal{N}(μ_{s_{n}},\sigma_{2}^2)

β_{i} \sim \mathcal{N}(μ_{c},\sigma_{c}^2)

γ \sim \mathcal{N}(μ_{d},\sigma_{d}^2)

ランダム係数$r_{i,n}$の事前分布のパラメータ$μ_{r_{i,n}}$にも事前分布が設定されていて、これを超事前分布という。
これは、$μ_{r_{i,n}}$が確率的に振る舞い$μ_{r_{i,n}}$の振る舞いのもと$r_{i,n}$も確率的に振る舞うということを示していて、$μ_{r_{i,n}}$→$r_{i,n}$の階層構造になっているので階層ベイズと呼ぶ。

このランダム係数$r_{i,n}$によって、個人で各説明変数の目的変数への影響度が異なるようになる。図にすると以下のようなイメージ。

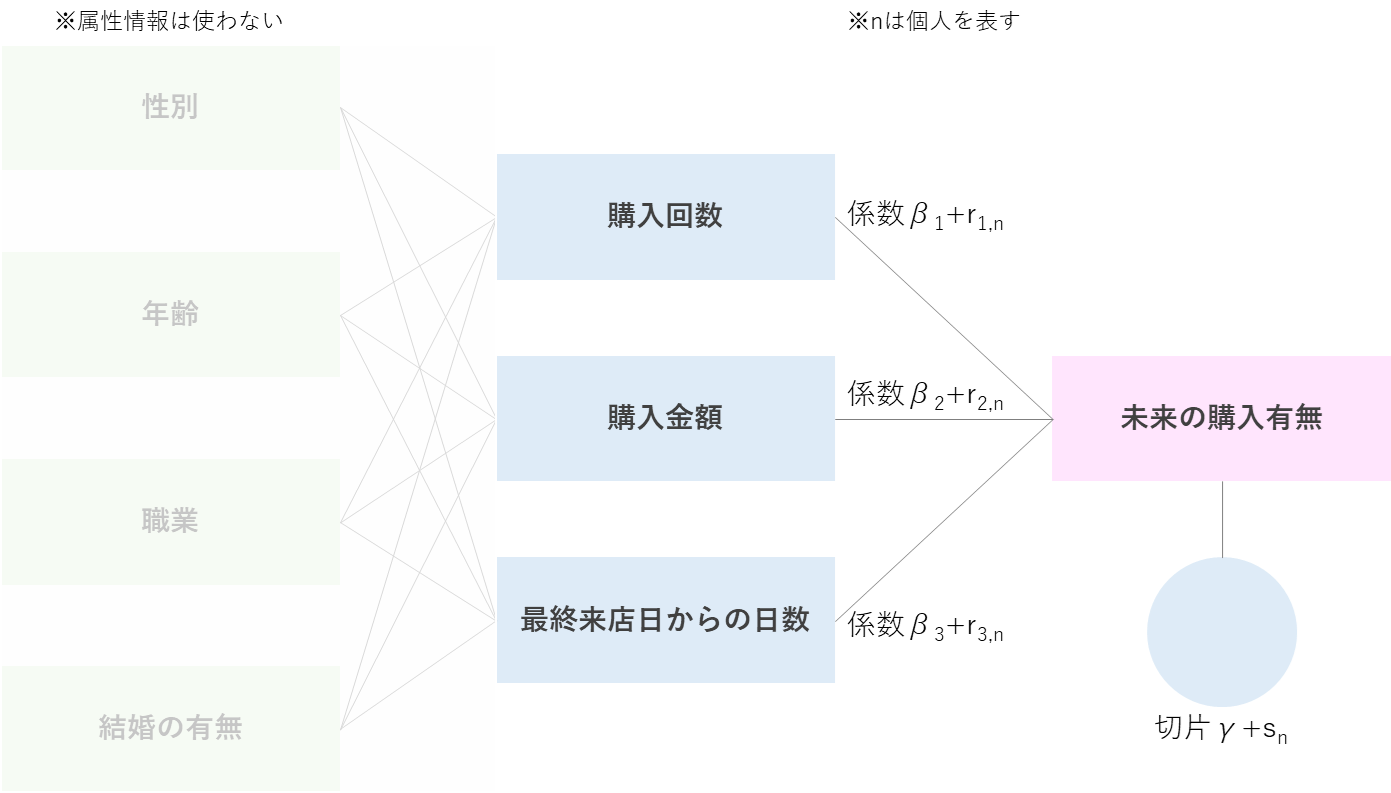
今回のデータ的には属性情報によってランダム係数が変動する設定なわけだが、属性情報を使わなくてもちゃんとランダム係数が変動して個人の異質性を捉えられるだろうか。

モデルの定義

ではモデルを定義する。
係数$β_{i}$と切片$γ$は固定効果として、事前分布に正規分布を仮定する。
ランダム係数$r_{i,n}$、ランダム切片$s_{n}$も、事前分布に正規分布を仮定するが、事前分布のパラメータに対して別の事前分布を設定する（超事前分布）。
あとはベイズロジスティック回帰モデルの時と同様、各係数と切片による線形モデルを"mu"と定義し、逆リンク関数はシグモイド関数、出力の分布はベルヌーイ分布とするようなモデルを想定。

# モデルの定義
with pm.Model() as model_random1:
    # coords
    model_random1.add_coord('data', values=range(train_df.shape[0]), mutable=True)
    model_random1.add_coord('var', values=purchasecols, mutable=True)

    # 説明変数
    x = pm.MutableData('x', train_df[purchasecols].to_numpy(), dims=('data', 'var'))
    y = pm.MutableData("y", train_df['purchase'].to_numpy(), dims=('data', ))

    # 推論パラメータの超事前分布
    super_mu_keisuu = pm.Normal('super_mu_keisuu', mu=0, sigma=1, dims=('var'))  # ランダム係数の平均の超事前分布
    super_mu_seppen = pm.Normal('super_mu_seppen', mu=0, sigma=1)  # ランダム切片の平均の超事前分布
    #super_sigma_keisuu = pm.HalfStudentT('super_sigma_keisuu', nu=4, dims=('var'))  # MCMC収束しなかったので設定しない
    #super_sigma_seppen = pm.HalfStudentT('super_sigma_seppen', nu=4)  #  MCMC収束しなかったので設定しない
    
    # 推論パラメータの事前分布
    coef_ = pm.Normal('coef', mu=0, sigma=1, dims=('var'))  # 係数の事前分布
    intercept_ = pm.Normal('intercept', mu=0, sigma=1)  # 切片の事前分布 
    r_coef_ = pm.Normal('r_coef_', mu=super_mu_keisuu, sigma=1, dims=('data', 'var'))  # ランダム係数の事前分布  データ×係数の数分の値がある
    r_intercept_ = pm.Normal('r_intercept_', mu=super_mu_seppen, sigma=1, dims=('data', ))  # ランダム切片の事前分布   データ分の値がある
    
    # linear model
    mu = pm.Deterministic("mu", pm.math.sum((coef_+r_coef_)*x, axis=1) + intercept_ + r_intercept_, dims=('data', ))
    # link function
    link = pm.Deterministic("link", pm.math.invlogit(mu), dims=('data', ))  # リンク関数
    # likelihood
    result = pm.Bernoulli("obs", p=link, observed=y, dims=('data', ))  # 尤度関数

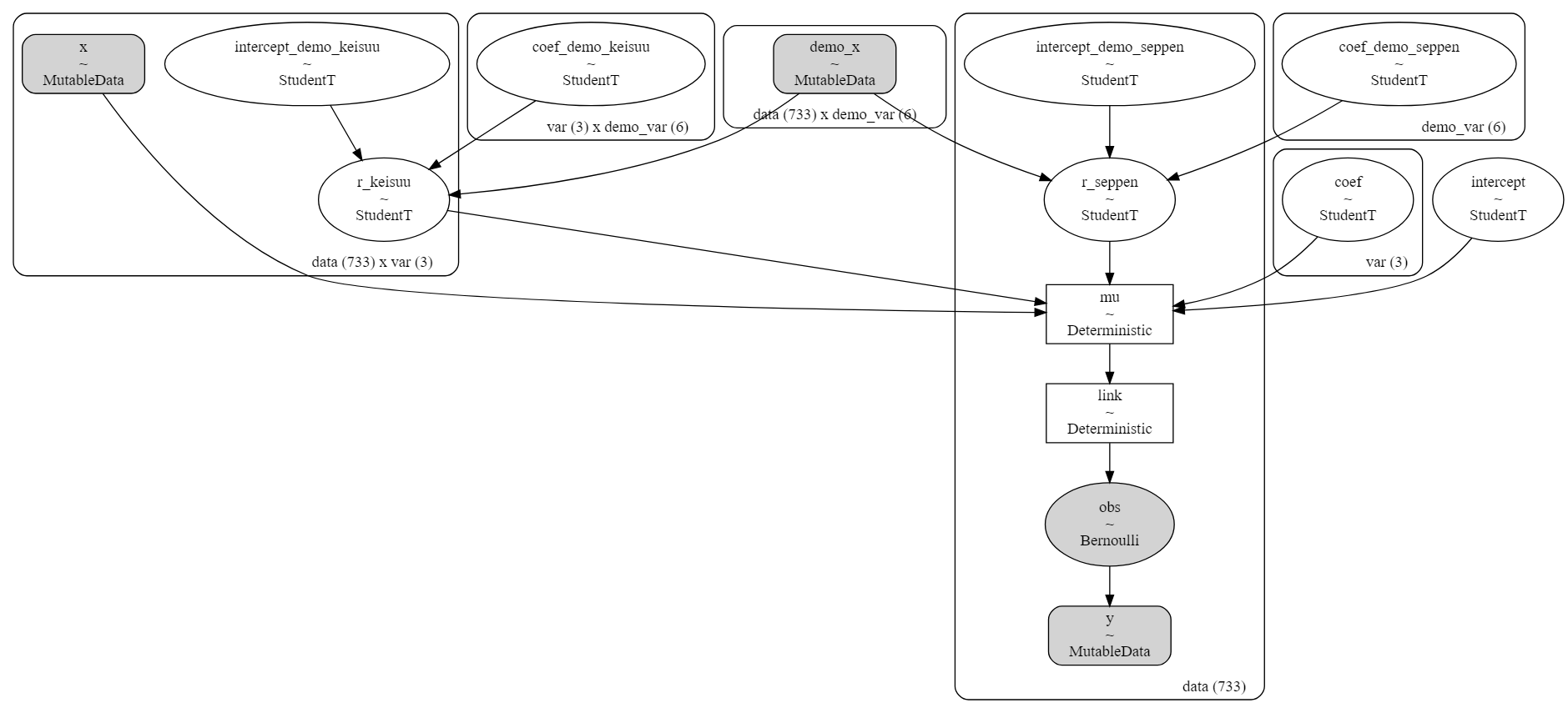
定義したDAG構造を見てみる。

# 構造
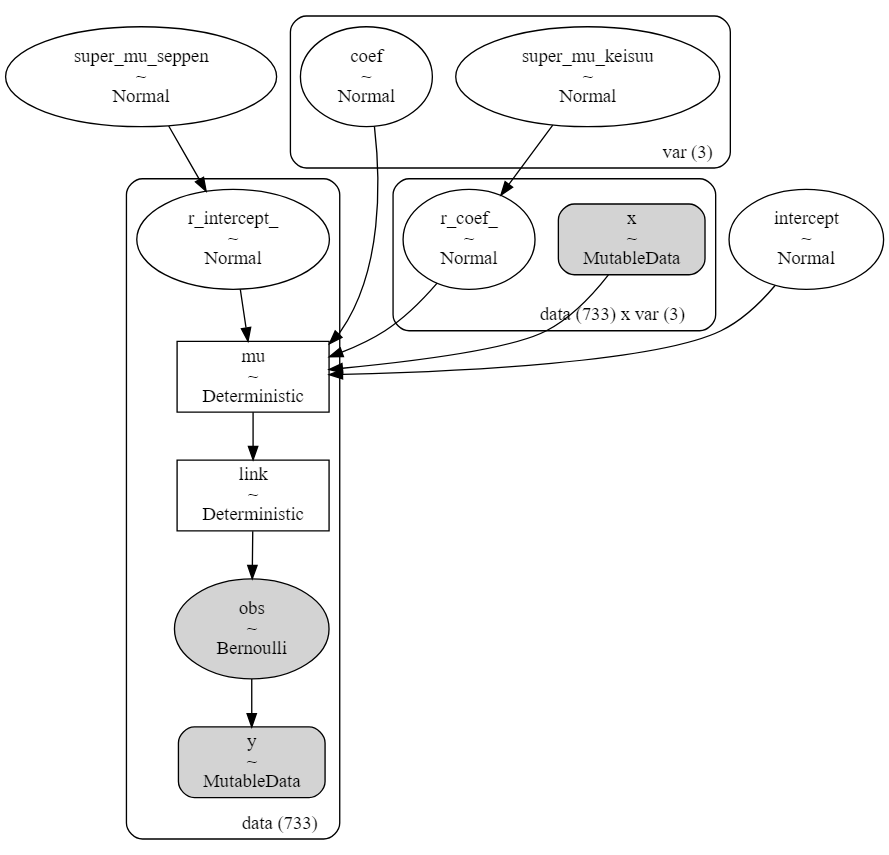
modeldag = pm.model_to_graphviz(model_random1)
display(modeldag)

正規分布を仮定している超事前分布がそれぞれランダム係数$r_{i,n}$、ランダム切片$s_{n}$の事前分布(r_coef_, r_intercept_)につながり、係数$β_{i}$と切片$γ$の事前分布とランダム係数$r_{i,n}$、ランダム切片$s_{n}$の事前分布と説明変数"x"は"mu"へとつながって線形モデルができ、"mu"に逆リンク関数が適用され、ベルヌーイ分布の出力を得る。

MCMC

MCMC実行。

%%time
# MCMC実行
# バックエンドでNumPyroで実行
with model_random1:
    # MCMCによる推論
    trace = pm.sample(draws=3000, tune=1000, chains=3, nuts_sampler="numpyro", random_seed=1, return_inferencedata=True)
# >> Wall time: 45.5 s
# データの保存 to_netcdfの利用
trace.to_netcdf('model_random1.nc')
# データの読み込み from_netcdfの利用
#trace = az.from_netcdf('model_random1.nc')

MCMCの収束を評価。
超事前分布のパラメータや係数$β_{i}$、切片$γ$の事後分布については、$\hat{R}$が1.1を超えてMCMCの収束が微妙なので、あまり良い推定はできていないかも。MCMCのサンプルサイズを変えたりした方がいいのかもしれないけど、とりあえずこのまま進む。

# MCMCの収束を評価
rhat_vals = az.rhat(trace).values()
# 最大のRhatを確認
result = np.max([np.max(i.values) for i in rhat_vals if i.name in ["coef", "intercept", "r_coef_", "r_intercept_"]])
print('Max rhat:', result)
# 1.1以上のRhatを確認
for i in rhat_vals:
    if np.max(i.values)>=1.1:
        print(i.name, np.max(i.values), np.mean(i.values), i.values.shape, sep='  ====>  ')

'''
# トレースプロットとか
# plot_trace
az.plot_trace(trace, backend_kwargs={"constrained_layout":True}, var_names=["coef", "intercept", "r_coef_", "r_intercept_"])
plt.show()

# forest plotでRハットと一緒に可視化
az.plot_forest(trace, combined=True, hdi_prob=0.95, r_hat=True, var_names=["r_coef_", "r_intercept_"])
plt.tight_layout()
plt.show()

# 事後分布の確認
az.plot_posterior(trace, hdi_prob=0.95, var_names=["coef_purchase"], ref_val=0, figsize=(20,30))
plt.tight_layout()
plt.show()

# Energy Plot
az.plot_energy(trace)
plt.show()
'''

Max rhat: 1.1499480242341165
super_mu_keisuu ====> 1.18613203591351 ====> 1.1350189779645905 ====> (3,)
super_mu_seppen ====> 1.1070281675590568 ====> 1.1070281675590568 ====> ()
coef ====> 1.1499480242341165 ====> 1.1094513189519961 ====> (3,)
intercept ====> 1.1020830748905863 ====> 1.1020830748905863 ====> ()

予測サンプル生成（学習データ）

特に意味は無いが、学習データの予測結果を見てみる。sample_posterior_predictiveで事後分布から予測サンプルを生成する。

# 事後分布
with model_random1:
    idata = pm.sample_posterior_predictive(trace)

# 学習データを使って予測
p_preds = idata.posterior_predictive['obs'].mean(dim=["chain"]).values  # chain平均
p_pred = idata.posterior_predictive['obs'].mean(dim=["chain", "draw"]).values  # chainとサンプル平均
y_pred = (p_pred >= 0.5).astype("int")  # 0.5以上を1
y_true = train_df['purchase'].to_numpy()  # 実際の購買有無
p_true = train_df['probabilities'].to_numpy()
result_summary(p_true, p_pred, y_true, y_pred)

• 評価指標（学習データ）
  accuracy_score 0.9672578444747613
precision_score 0.957983193277311
recall_score 0.8571428571428571
f1_score 0.9047619047619048

• 混同行列（学習データ）
  
  （他指標は省略）

推定パラメータ確認

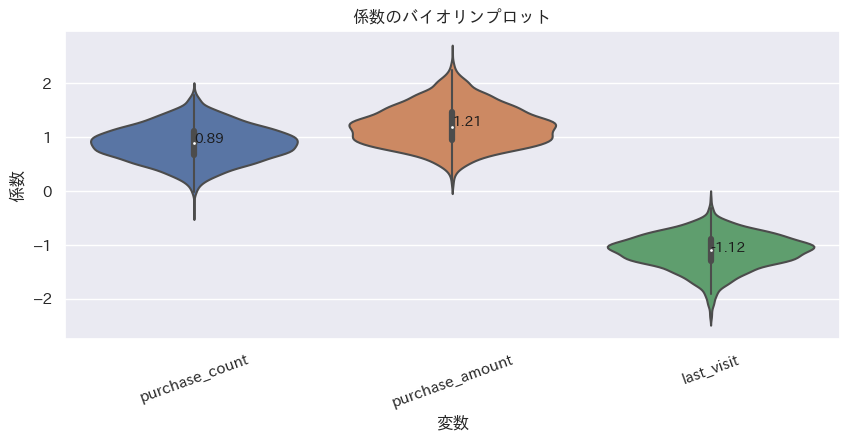
推定した係数$β_{i}$の平均と、分布を確認する。
平均は'purchase_count': 0.89, 'purchase_amount': 1.21, 'last_visit': -1.12であった。
ベイズロジスティック回帰モデルの結果が'purchase_count': 1.19, 'purchase_amount': 1.91, 'last_visit': -1.73なので傾向は似てるが、絶対値はちょっと控えめになっている。

corf_df = pd.DataFrame(trace.posterior['coef'].mean(dim=["chain"]).values, columns=purchasecols)
coef_dict = {i:round(corf_df[i].mean(),2) for i in purchasecols}
print(coef_dict)
plot_violin(corf_df, order=None, xlabel='変数', ylabel='係数', title='係数のバイオリンプロット')

ランダム係数の分布も見てみる。データの最初の100人のランダム係数の箱ひげ図をプロット。

indivisual_count, indivisual_amount, indivisual_last_visit = random_coef_effect(trace, 'r_coef_')

indivisual_plot(indivisual_count, ylabel='購入回数の係数', title='"購入回数"の係数が各個人の属性情報によってばらつくことをモデル化', brk=True)
indivisual_plot(indivisual_amount, ylabel='購入金額の係数', title='"購入金額"の係数が各個人の属性情報によってばらつくことをモデル化', brk=True)
indivisual_plot(indivisual_last_visit, ylabel='最終来店からの日数の係数', title='"最終来店からの日数"の係数が各個人の属性情報によってばらつくことをモデル化', brk=True)

• 1箱ひげ＝1個人の箱ひげ図
  購入回数にかかるランダム係数
  
  購入金額にかかるランダム係数
  
  最終来店からの日数にかかるランダム係数
  

あっれれ～！みんなランダム係数に差が無いじゃーん。
女性で学生なら購入回数の係数が大きく、男性でProfessionalなら購入金額の係数が大きく、年齢が40以上で未婚なら最終来店日からの日数の係数が負の方向に大きい設定なので、その3ケースの人たちの係数の平均を見てみる。

# 女性で学生ならcoef_****1, 男性でProfessionalならcoef_****2, 年齢が40以上で未婚ならcoef_****3
# 女性で学生なら購入回数の係数が大きく、
# 男性でProfessionalなら購入金額の係数が大きく、
# 年齢が40以上で未婚なら最終来店日からの日数の係数が負の方向に大きいはず
indivisual_summary_plot(train_df, democols, indivisual_count, indivisual_amount, indivisual_last_visit)

差が無くて草。やっぱ属性情報は必要か？

予測サンプル生成（テストデータ）

一応、未知データとしてテストデータの推論もしておく。（めんどうなので内容については言及しない。）
pm.set_dataでテストデータの情報に更新した後に、pm.sample_posterior_predictive()で予測を行う。

# テストデータの推論
with model_random1:
    pm.set_data({'x':test_df[purchasecols].to_numpy()
                 , 'y': np.zeros(len(test_df[purchasecols].to_numpy()))  # yは未知とする。実際の答えはtest_df['purchase'].to_numpy()。
                }
                , coords={"data": (np.arange(test_df.shape[0]))+train_df.shape[0]}
               )
    trace.extend(pm.sample_posterior_predictive(trace))

# テストデータを使って予測
p_preds_test = trace.posterior_predictive["obs"].mean(dim=["chain"]).values  # chain平均
p_pred_test = trace.posterior_predictive["obs"].mean(dim=["chain", "draw"]).values  # chainとサンプル平均
y_pred_test = (p_pred_test >= 0.5).astype("int")  # 0.5以上を1
y_true_test = test_df['purchase'].to_numpy()  # 実際の購買有無
p_true_test = test_df['probabilities'].to_numpy()
result_summary(p_true_test, p_pred_test, y_true_test, y_pred_test)

• 評価指標（テストデータ）
  accuracy_score 0.9264305177111717
precision_score 0.8225806451612904
recall_score 0.7611940298507462
f1_score 0.7906976744186047

• 混同行列（テストデータ）
  
  （他指標は省略）

階層ベイズ二項ロジットモデル: 属性情報あり 固定効果あり ランダム効果あり

ランダム係数に全然差が無かったので、属性情報を入れて再度モデルを構築してみる。
このモデルでは、ランダム係数$r_{i,n}$、ランダム切片$s_{n}$の事前分布のパラメータが属性情報によって決まるという仮定を置いている。
購買行動$x$の係数$β_{i}$、切片$γ$、ランダム係数$r_{i,n}$、ランダム切片$s_{n}$、ランダム係数$r_{i,n}$の事前分布のパラメータ$μ_{r_{i,n}}$、ランダム切片$s_{n}$の事前分布のパラメータ$μ_{s_{n}}$、属性情報$z$の係数$α_{j}$、切片$δ$を用いてロジスティック回帰モデルを数式で表すと、以下のような式になる。（この数式では超事前分布や事前分布は正規分布を仮定。でも実際のコードではStudentTにしている。）

\log (\frac{p}{1-p})=(β_{1}+r_{1,n})x_{1}+(β_{2}+r_{2,n})x_{2}+(β_{3}+r_{3,n})x_{3}+γ+s_{n}

β_{i} \sim \mathcal{N}(μ_{c},\sigma_{c}^2)

γ \sim \mathcal{N}(μ_{d},\sigma_{d}^2)

r_{i,n} \sim \mathcal{N}(μ_{r_{i,n}},\sigma_{1}^2)

s_{n} \sim \mathcal{N}(μ_{s_{n}},\sigma_{2}^2)

μ_{r_{i,n}}=α_{1}z_{1}+α_{2}z_{2}+ … +α_{j}z_{j}+δ

μ_{s_{n}}=α_{1}z_{1}+α_{2}z_{2}+ … +α_{j}z_{j}+δ

α_{j} \sim \mathcal{N}(μ_{a},\sigma_{a}^2)

δ \sim \mathcal{N}(μ_{b},\sigma_{b}^2)

なかなか複雑になってきた気がする。

モデルの定義

ではモデルを定義していく。基本的に上記の数式通りにモデルを組んでいる。
ただ、「階層モデルの分散パラメータの事前分布について発表しました」や「ロバストなベイズ的回帰分析のための新しい誤差分布 (理論編)」を見て、もしかしてt分布の方が良かったりするのかな？と思って事前分布はpm.StudentT()でt分布に設定している。正規分布にしてもそんなに結果は変わらなかったけど。

# モデルの定義
with pm.Model() as model_random2:
    # coords
    model_random2.add_coord('data', values=range(train_df.shape[0]), mutable=True)
    model_random2.add_coord('var', values=purchasecols, mutable=True)
    model_random2.add_coord('demo_var', values=democols, mutable=True)

    # 説明変数
    x = pm.MutableData('x', train_df[purchasecols].to_numpy(), dims=('data', 'var'))
    y = pm.MutableData("y", train_df['purchase'].to_numpy(), dims=('data', ))
    demo_x = pm.MutableData('demo_x', train_df[democols].to_numpy(), dims=('data', 'demo_var'))

    # 超事前分布
    coef_demo_keisuu = pm.StudentT('coef_demo_keisuu', nu=4, mu=0, sigma=1.0, dims=('var', 'demo_var'))  # ランダム係数の平均の超事前分布
    intercept_demo_keisuu = pm.StudentT('intercept_demo_keisuu', nu=4, mu=0.0, sigma=1.0, dims=('data', 'var'))  # ランダム係数の平均の超事前分布
    #rsigma_keisuu = pm.HalfStudentT('rsigma_keisuu', nu=4, dims=('data', 'var'))  #  MCMC収束しなかったので設定しない
    coef_demo_seppen = pm.StudentT('coef_demo_seppen', nu=4, mu=0, sigma=1.0, dims=('demo_var', ))  # ランダム切片の平均の超事前分布
    intercept_demo_seppen = pm.StudentT('intercept_demo_seppen', nu=4, mu=0.0, sigma=1.0, dims=('data', ))  # ランダム切片の平均の超事前分布
    #rsigma_seppen = pm.HalfStudentT('rsigma_seppen', nu=4, dims=('data', ))#pm.HalfCauchy('rsigma', mu=0.0, sigma=1)  #  MCMC収束しなかったので設定しない
    
    # 推論パラメータの事前分布    
    coef_ = pm.StudentT('coef', nu=4, mu=0.0, sigma=1, dims=('var', ))  # 固定効果
    intercept_ = pm.StudentT('intercept', nu=4, mu=0.0, sigma=1)  # 固定効果
    r_keisuu = pm.StudentT('r_keisuu', nu=4, mu=coef_demo_keisuu.dot(demo_x.T).T + intercept_demo_keisuu, sigma=1, dims=('data', 'var'))  # ランダム効果 データ×係数の数分の値がある
    r_seppen = pm.StudentT('r_seppen', nu=4, mu=coef_demo_seppen.dot(demo_x.T).T + intercept_demo_seppen, sigma=1, dims=('data', ))  # ランダム効果 データの数分の値がある
    
    # linear model
    mu = pm.Deterministic("mu", pm.math.sum((coef_ + r_keisuu) * x, axis=1) + intercept_ + r_seppen, dims=('data', ))
    # link function
    link = pm.Deterministic("link", pm.math.invlogit(mu), dims=('data', ))
    # likelihood
    result = pm.Bernoulli("obs", p=link, observed=y, dims=('data', ))

# 構造
modeldag = pm.model_to_graphviz(model_random2)
display(modeldag)

MCMC

定義できたので、MCMC。

%%time
# MCMC実行
# バックエンドでNumPyroで実行
with model_random2:
    # MCMCによる推論
    trace = pm.sample(draws=3000, tune=1000, chains=3, nuts_sampler="numpyro", random_seed=1, return_inferencedata=True)
# >> Wall time: 6min 42s

# データの保存 to_netcdfの利用
trace.to_netcdf('model_random2.nc')
# データの読み込み from_netcdfの利用
#trace = az.from_netcdf('model_random2.nc')

すべての$\hat{R}$が1.1未満だったので収束は問題なさそう。

# MCMCの収束を評価
rhat_vals = az.rhat(trace).values()
# 最大のRhatを確認
result = np.max([np.max(i.values) for i in rhat_vals if i.name in ["coef", "intercept", "r_coef_", "r_intercept_"]])
print('Max rhat:', result)
# 1.1以上のRhatを確認
for i in rhat_vals:
    if np.max(i.values)>=1.1:
        print(i.name, np.max(i.values), np.mean(i.values), i.values.shape, sep='  ====>  ')

'''
# Energy Plot
az.plot_energy(trace)
plt.show()
'''

Max rhat: 1.0182392695050588

予測サンプル生成（学習データ）

~~
（特に意味が無いので、学習データの推論結果は割愛）
~~

推定パラメータ確認

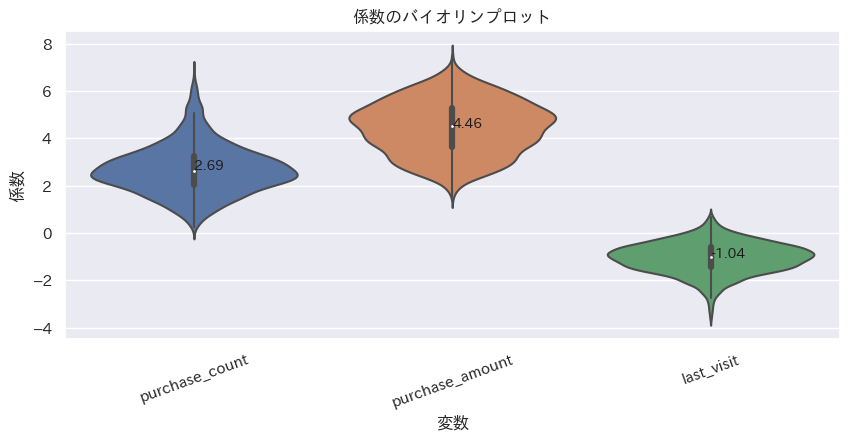
推定した係数$β_{i}$の平均と、分布を確認する。
平均は'purchase_count': 2.69, 'purchase_amount': 4.46, 'last_visit': -1.04であった。
ベイズロジスティック回帰モデルの結果が'purchase_count': 1.19, 'purchase_amount': 1.91, 'last_visit': -1.73なので固定効果はまあまあ違った推定になったような気がする。

corf_df = pd.DataFrame(trace.posterior['coef'].mean(dim=["chain"]).values, columns=purchasecols)
coef_dict = {i:round(corf_df[i].mean(),2) for i in purchasecols}
print(coef_dict)
plot_violin(corf_df, order=None, xlabel='変数', ylabel='係数', title='係数のバイオリンプロット')

ランダム係数の分布も見てみる。データの最初の100人のランダム係数の箱ひげ図をプロット。

indivisual_count, indivisual_amount, indivisual_last_visit = random_coef_effect(trace, 'r_keisuu')

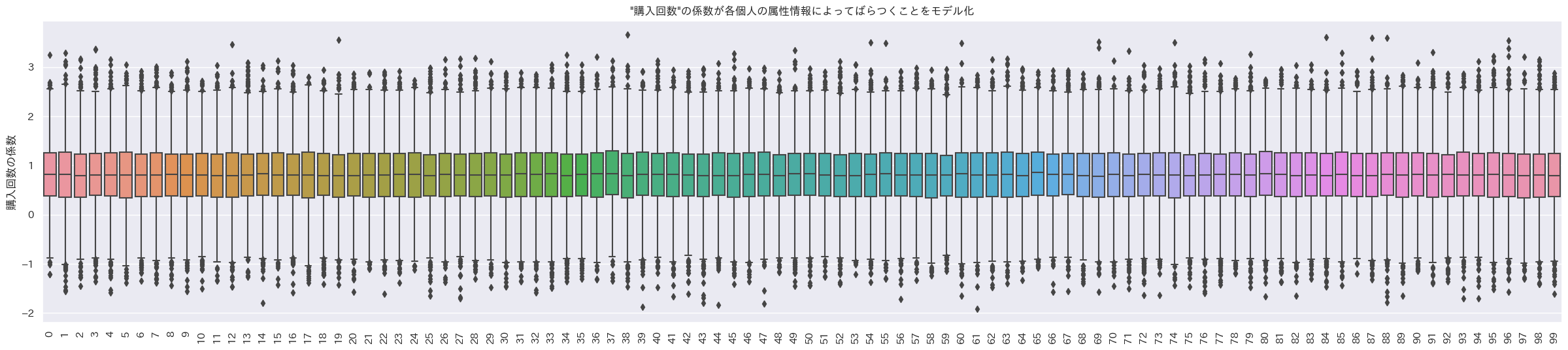
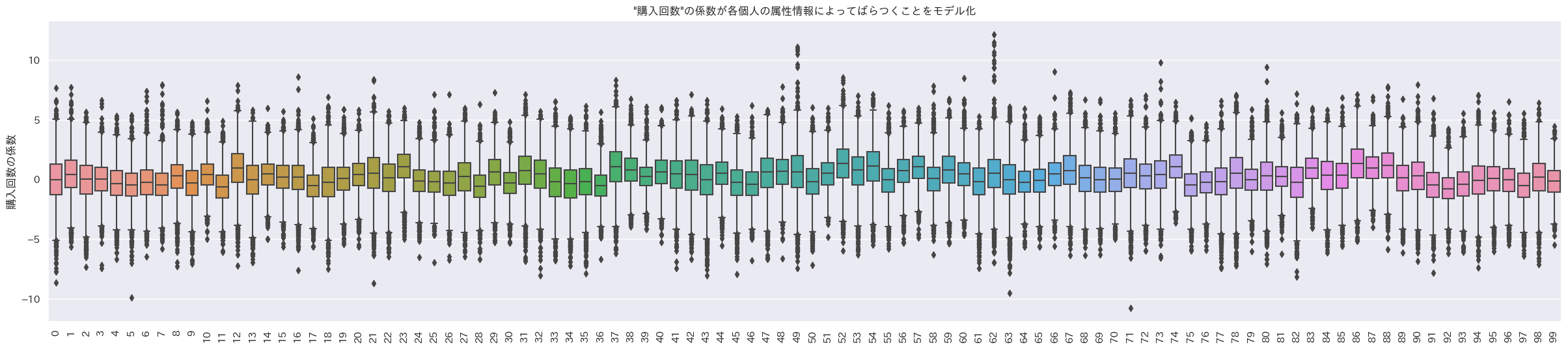
indivisual_plot(indivisual_count, ylabel='購入回数の係数', title='"購入回数"の係数が各個人の属性情報によってばらつくことをモデル化', brk=True)
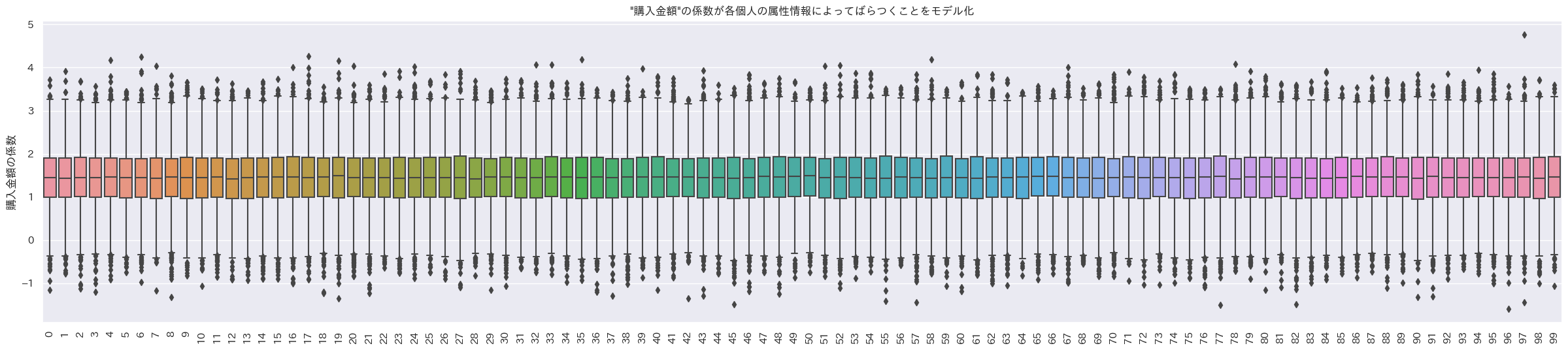
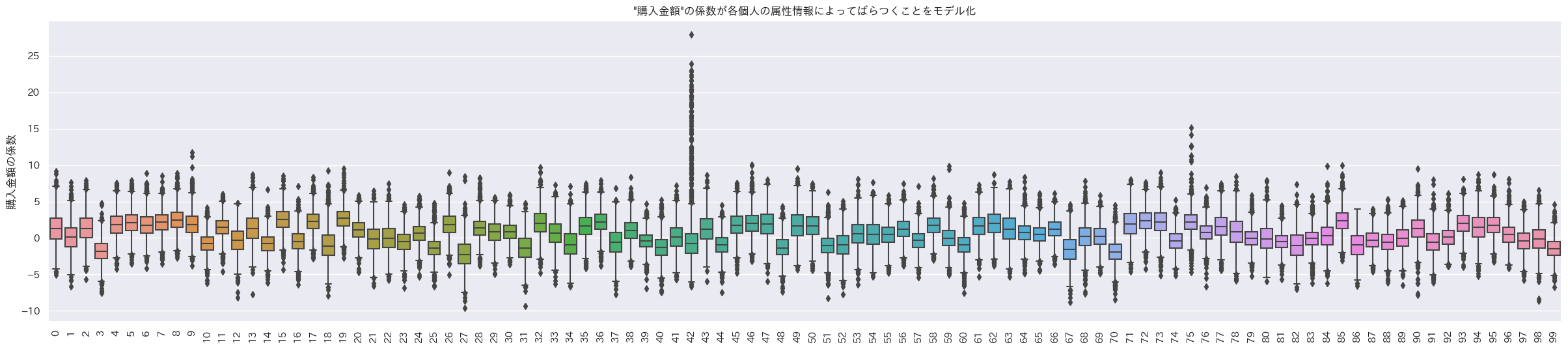
indivisual_plot(indivisual_amount, ylabel='購入金額の係数', title='"購入金額"の係数が各個人の属性情報によってばらつくことをモデル化', brk=True)
indivisual_plot(indivisual_last_visit, ylabel='最終来店からの日数の係数', title='"最終来店からの日数"の係数が各個人の属性情報によってばらつくことをモデル化', brk=True)

• 1箱ひげ＝1個人の箱ひげ図
  購入回数にかかるランダム係数
  
  購入金額にかかるランダム係数
  
  最終来店からの日数にかかるランダム係数
  

おお、個人でランダム係数の値が異なるように見える。

女性で学生なら購入回数の係数が大きく、男性でProfessionalなら購入金額の係数が大きく、年齢が40以上で未婚なら最終来店日からの日数の係数が負の方向に大きい設定なので、その3ケースの人たちの係数の平均を見てみる。

# 女性で学生ならcoef_****1, 男性でProfessionalならcoef_****2, 年齢が40以上で未婚ならcoef_****3
# 女性で学生なら購入回数の係数が大きく、
# 男性でProfessionalなら購入金額の係数が大きく、
# 年齢が40以上で未婚なら最終来店日からの日数の係数が負の方向に大きいはず
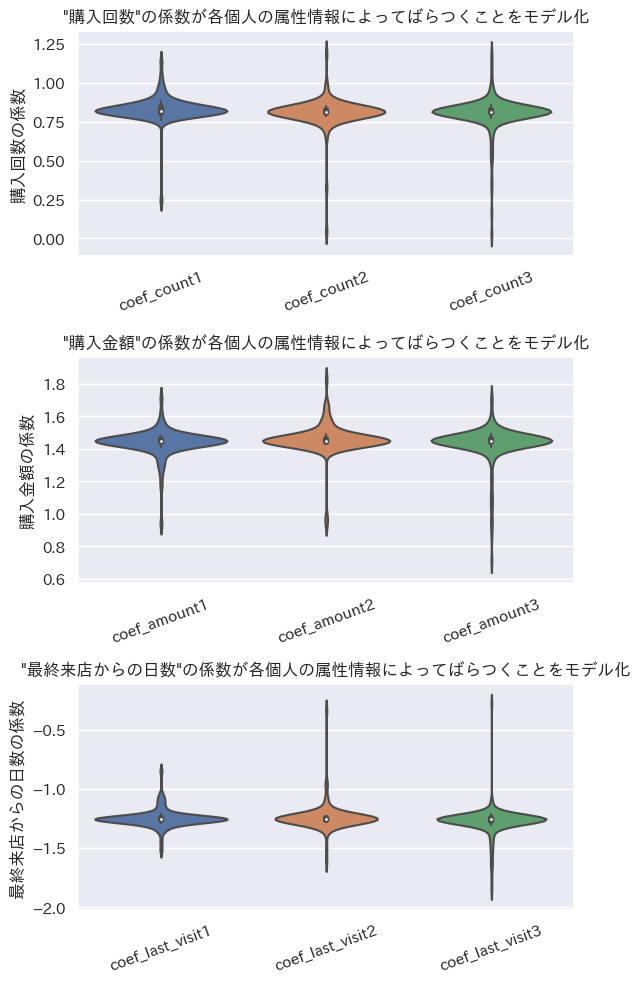
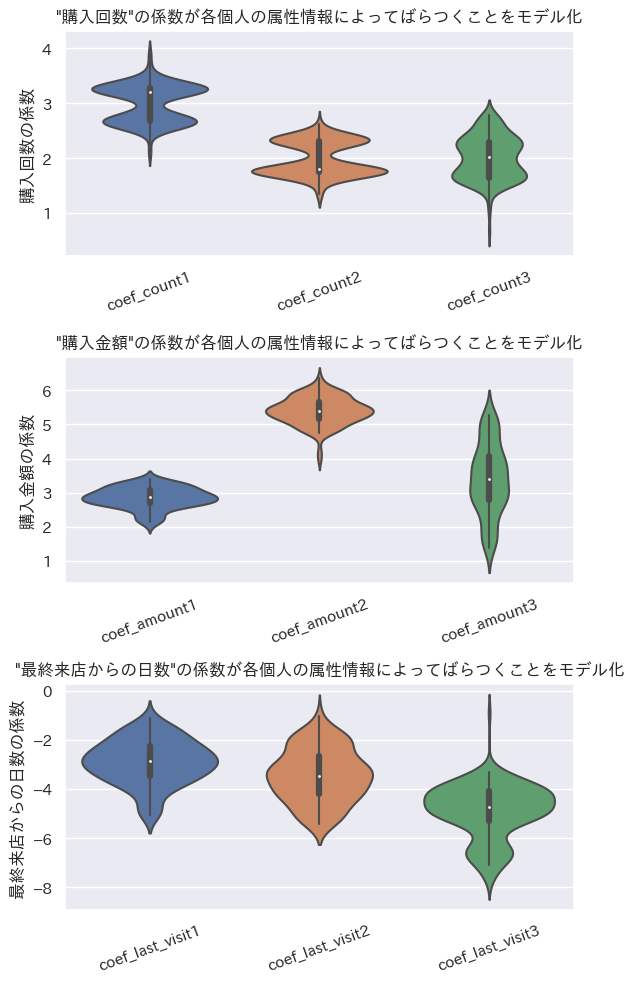
indivisual_summary_plot(train_df, democols, indivisual_count, indivisual_amount, indivisual_last_visit)

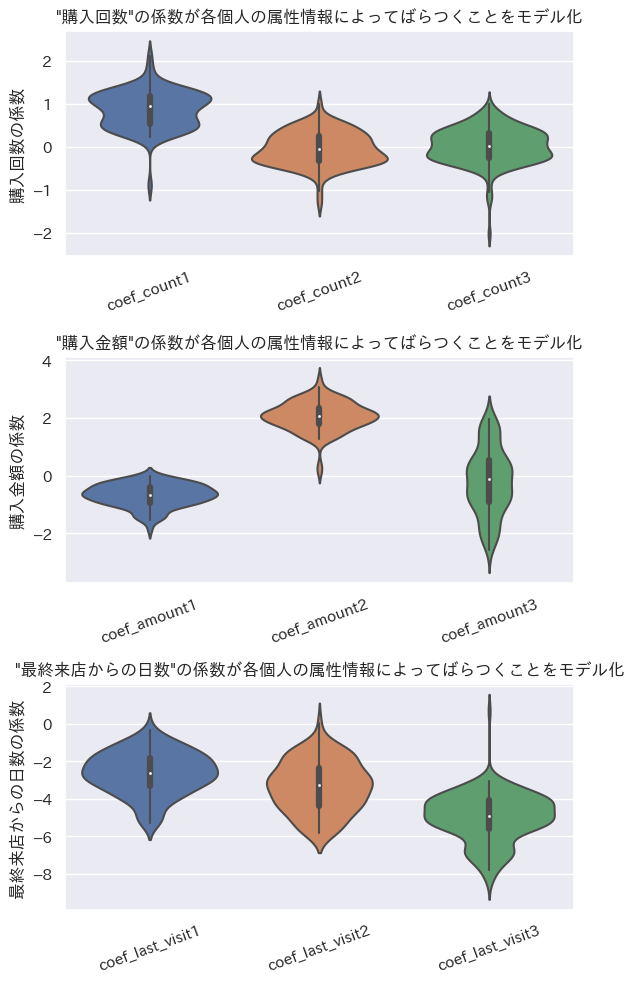
購入回数は女性で学生のケースが一番ランダム係数の平均値が正の方向に大きい。
購入金額は男性でProfessionalのケースが一番ランダム係数の平均値が正の方向に大きい。
最終来店日からの日数は年齢が40以上で未婚のケースが一番ランダム係数の平均値が負の方向大きい。
ということでデータ作成時の設定どおりの結果が出たのではないだろうか。

予測サンプル生成（テストデータ）

一応、未知データとしてテストデータの推論もしておく。
pm.set_dataでテストデータの情報に更新した後に、pm.sample_posterior_predictive()で予測を行う。
テストデータはf1_score 0.78と、まあぼちぼちの結果。

# テストデータの推論
with model_random2:
    pm.set_data({'demo_x':test_df[democols].to_numpy()
                 , 'x':test_df[purchasecols].to_numpy()
                 , 'y': np.zeros(len(test_df[purchasecols].to_numpy()))  # yは未知とする。実際の答えはtest_df['purchase'].to_numpy()。
                }
                , coords={"data": (np.arange(test_df.shape[0]))+train_df.shape[0]}
               )
    trace.extend(pm.sample_posterior_predictive(trace))

# テストデータを使って予測
p_preds_test = trace.posterior_predictive["obs"].mean(dim=["chain"]).values  # chain平均
p_pred_test = trace.posterior_predictive["obs"].mean(dim=["chain", "draw"]).values  # chainとサンプル平均
y_pred_test = (p_pred_test >= 0.5).astype("int")  # 0.5以上を1
y_true_test = test_df['purchase'].to_numpy()  # 実際の購買有無
p_true_test = test_df['probabilities'].to_numpy()
result_summary(p_true_test, p_pred_test, y_true_test, y_pred_test)

• 評価指標（テストデータ）
  accuracy_score 0.9237057220708447
precision_score 0.819672131147541
recall_score 0.746268656716418
f1_score 0.7812500000000001

• 混同行列（テストデータ）
  
  （他指標は省略）

階層ベイズ二項ロジットモデル: 属性情報あり 固定効果なし ランダム効果あり

ここで一つ思いついた。
固定効果＋ランダム効果でランダム効果を属性情報で推定するというアプローチをやってみたわけだが、固定効果をなくしてランダム効果だけにしてそのランダム効果を属性情報で推定するってのもありなのではと。
イメージ的には固定効果としていた係数$β_{i}$と切片$γ$をランダム効果として属性情報から推定する感じ。その場合係数$β_{i,n}$と切片$γ_{n}$になるか。
購買行動$x$の係数$β_{i,n}$、切片$γ_{n}$、係数$β_{i,n}$の事前分布のパラメータ$μ_{β_{i,n}}$、切片$γ_{n}$の事前分布のパラメータ$μ_{γ_{n}}$、属性情報$z$の係数$α_{j}$、切片$δ$を用いてロジスティック回帰モデルを数式で表すと、以下のような式になる。(この数式では超事前分布や事前分布は正規分布を仮定。でも実際のコードではStudentTにしている。)

\log (\frac{p}{1-p})=β_{1,n}x_{1}+β_{2,n}x_{2}+β_{3,n}x_{3}+γ_{n}

β_{i,n} \sim \mathcal{N}(μ_{β_{i,n}},\sigma_{1}^2)

γ_{n} \sim \mathcal{N}(μ_{γ_{n}},\sigma_{2}^2)

μ_{β_{i,n}}=α_{1}z_{1}+α_{2}z_{2}+ … +α_{j}z_{j}+δ

μ_{γ_{n}}=α_{1}z_{1}+α_{2}z_{2}+ … +α_{j}z_{j}+δ

α_{j} \sim \mathcal{N}(μ_{a},\sigma_{a}^2)

δ_{i} \sim \mathcal{N}(μ_{b},\sigma_{b}^2)

モデルの定義

モデルを定義していく。事前分布はpm.StudentT()でt分布に設定している。正規分布にしてもそんなに結果は変わらなかったけど。

# モデルの定義
with pm.Model() as model_random3:
    # coords
    model_random3.add_coord('data', values=range(train_df.shape[0]), mutable=True)
    model_random3.add_coord('demo_var', values=democols, mutable=True)
    model_random3.add_coord('purchase_var', values=purchasecols, mutable=True)

    # 変数
    demo_x = pm.MutableData('demo_x', train_df[democols].to_numpy(), dims=('data', 'demo_var'))
    purchase_x = pm.MutableData('purchase_x', train_df[purchasecols].to_numpy(), dims=('data', 'purchase_var'))
    y = pm.MutableData("y", train_df['purchase'].to_numpy(), dims=('data', ))

    # 属性情報の推論パラメータの事前分布(超事前分布)
    coef_demo = pm.StudentT('coef_demo', mu=0, sigma=1, nu=4, dims=('purchase_var', "demo_var")) # pm.StudentT('coef_demo', mu=0, sigma=1, nu=4, dims=('purchase_var', "demo_var"))# pm.Normal('coef_demo', mu=0, sigma=1, dims=('purchase_var', "demo_var"))
    intercept_demo = pm.StudentT('intercept_demo', mu=0, sigma=1, nu=4, dims=('purchase_var', )) # pm.StudentT('intercept_demo', mu=0, sigma=1, nu=4, dims=('purchase_var', ))# pm.Normal('intercept_demo', mu=0, sigma=1, dims=('purchase_var', ))
    coef_demo_intercept = pm.StudentT('coef_demo_intercept', mu=0, sigma=1, nu=4, dims=("demo_var", )) # pm.StudentT('coef_demo_intercept', mu=0, sigma=1, nu=4, dims=("demo_var", ))# pm.Normal('coef_demo_intercept', mu=0, sigma=1, dims=("demo_var", ))
    intercept_demo_intercept = pm.StudentT('intercept_demo_intercept', mu=0, sigma=1, nu=4) # pm.StudentT('intercept_demo_intercept', mu=0, sigma=1, nu=4, dims=('data', ))# pm.Normal('intercept_demo_intercept', mu=0, sigma=1, dims=('data', ))

    #sigma_coef_purchase = pm.HalfStudentT('sigma_coef_purchase', nu=4)
    #sigma_intercept_purchase = pm.HalfStudentT('sigma_intercept_purchase', nu=4)
    
    # 説明変数の推論パラメータの事前分布
    #ccoef_purchase = pm.Deterministic("coef_purchase", coef_demo.dot(demo_x.T).T + intercept_demo, dims=("data", 'purchase_var'))  # データ分の値がある
    coef_purchase = pm.StudentT('coef_purchase', nu=4, mu=coef_demo.dot(demo_x.T).T + intercept_demo, sigma=1, dims=("data", 'purchase_var'))
    intercept_purchase = pm.StudentT('intercept_purchase', nu=4, mu=coef_demo_intercept.dot(demo_x.T).T + intercept_demo_intercept, sigma=1, dims=('data', ))

    # linear model
    #mu = pm.Normal("mu", mu=pm.math.sum(coef_purchase*purchase_x, axis=1) + intercept_purchase, sigma=1.0, dims=('data', ))  # データ分の値がある
    mu = pm.Deterministic("mu", pm.math.sum(coef_purchase*purchase_x, axis=1) + intercept_purchase, dims=('data', ))  # データ分の値がある
    # link function
    link = pm.Deterministic("link", pm.math.invlogit(mu), dims=('data', ))
    # likelihood
    results = pm.Bernoulli("obs", p=link, observed=y, dims=('data', ))

# 構造
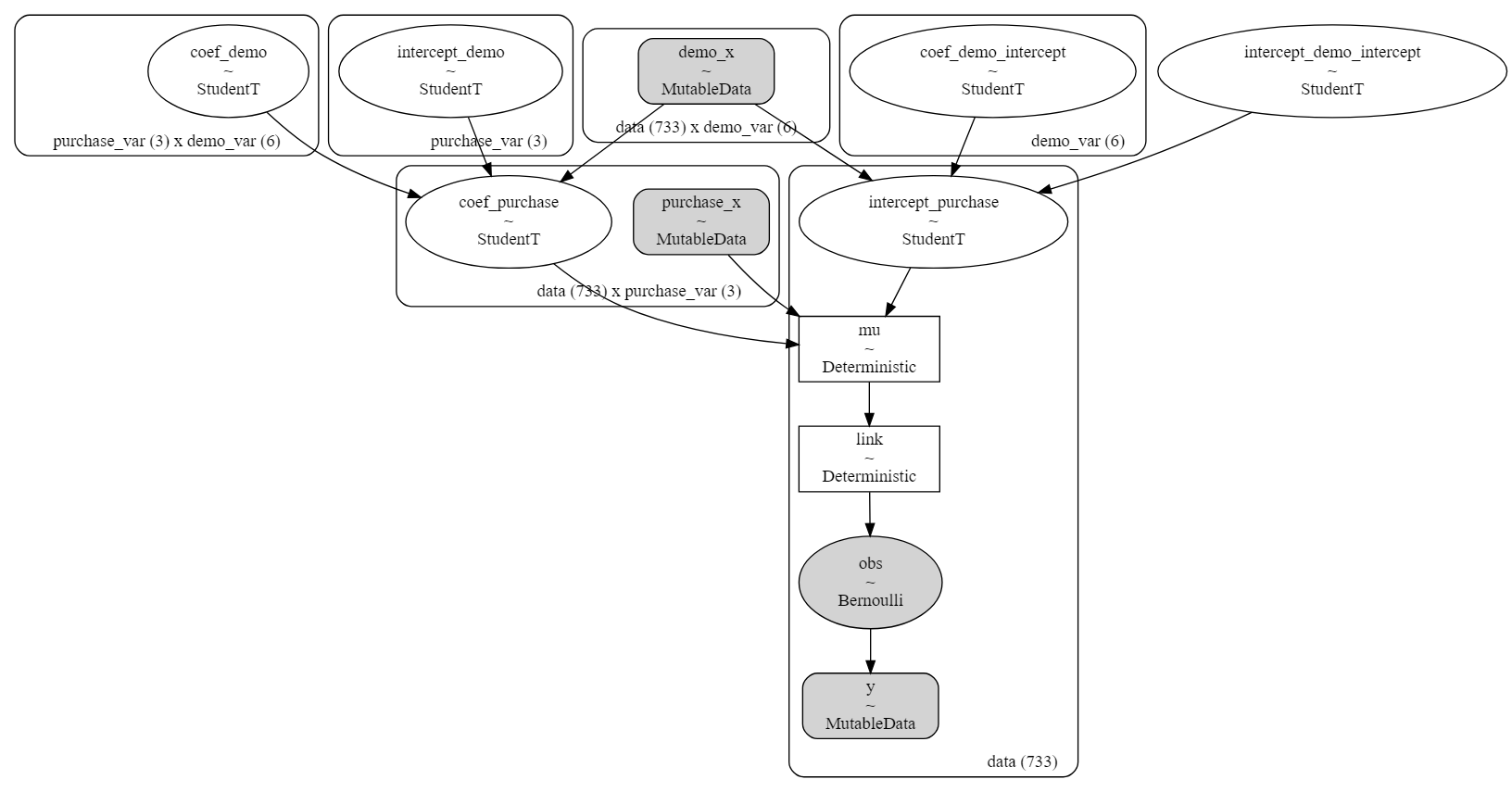
modeldag = pm.model_to_graphviz(model_random3)
display(modeldag)

MCMC

定義できたので、MCMC。

%%time
# MCMC実行
# バックエンドでNumPyroで実行
with model_random3:
    # MCMCによる推論
    trace = pm.sample(draws=3000, tune=1000, chains=3, nuts_sampler="numpyro", random_seed=1, return_inferencedata=True)
# >> Wall time: 3min 23s

# データの保存 to_netcdfの利用
trace.to_netcdf('model_random3.nc')
# データの読み込み from_netcdfの利用
#trace = az.from_netcdf('model_random3.nc')

すべての$\hat{R}$が1.1未満だったので収束は問題なさそう。

# MCMCの収束を評価
rhat_vals = az.rhat(trace).values()
# 最大のRhatを確認
result = np.max([np.max(i.values) for i in rhat_vals if i.name in ["coef_purchase", "intercept_purchase", "r_coef_", "r_intercept_"]])
print('Max rhat:', result)
# 1.1以上のRhatを確認
for i in rhat_vals:
    if np.max(i.values)>=1.1:
        print(i.name, np.max(i.values), np.mean(i.values), i.values.shape, sep='  ====>  ')

'''
# plot_trace
az.plot_trace(trace, backend_kwargs={"constrained_layout":True}, var_names=["coef_purchase", "intercept_purchase"])
plt.show()

# forest plotでRハットと一緒に可視化
az.plot_forest(trace, combined=True, hdi_prob=0.95, r_hat=True, var_names=["coef_purchase"])
plt.tight_layout()
plt.show()

# 事後分布の確認
az.plot_posterior(trace, hdi_prob=0.95, var_names=["coef_purchase"], ref_val=0, figsize=(20,30))
plt.tight_layout()
plt.show()

# Energy Plot
az.plot_energy(trace)
plt.show()
'''

Max rhat: 1.015216509556051

予測サンプル生成（学習データ）

~~
（特に意味が無いので、学習データの推論結果は割愛）
~~

推定パラメータ確認

今回の階層ベイズ二項ロジットモデル3では固定効果は無いので、そのまま$β_{i,n}$をランダム係数として分布を見てみる。データの最初の100人のランダム係数の箱ひげ図をプロット。

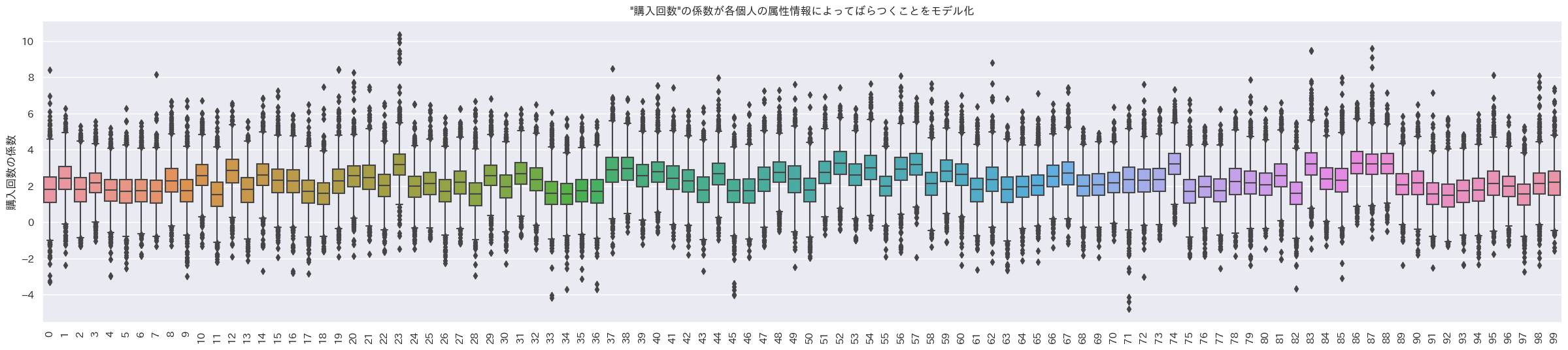
indivisual_count, indivisual_amount, indivisual_last_visit = random_coef_effect(trace, 'coef_purchase')

indivisual_plot(indivisual_count, ylabel='購入回数の係数', title='"購入回数"の係数が各個人の属性情報によってばらつくことをモデル化', brk=True)
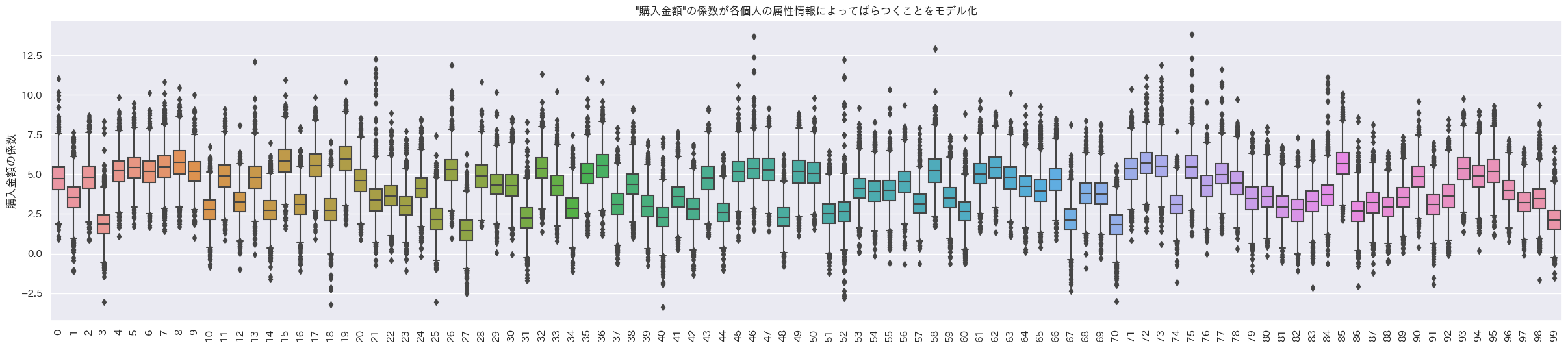
indivisual_plot(indivisual_amount, ylabel='購入金額の係数', title='"購入金額"の係数が各個人の属性情報によってばらつくことをモデル化', brk=True)
indivisual_plot(indivisual_last_visit, ylabel='最終来店からの日数の係数', title='"最終来店からの日数"の係数が各個人の属性情報によってばらつくことをモデル化', brk=True)

• 1箱ひげ＝1個人の箱ひげ図
  購入回数にかかるランダム係数
  
  購入金額にかかるランダム係数
  
  最終来店からの日数にかかるランダム係数
  

うん、これも個人でランダム係数の値が異なるように見えるね。

女性で学生なら購入回数の係数が大きく、男性でProfessionalなら購入金額の係数が大きく、年齢が40以上で未婚なら最終来店日からの日数の係数が負の方向に大きい設定なので、その3ケースの人たちの係数の平均を見てみる。

# 女性で学生ならcoef_****1, 男性でProfessionalならcoef_****2, 年齢が40以上で未婚ならcoef_****3
# 女性で学生なら購入回数の係数が大きく、
# 男性でProfessionalなら購入金額の係数が大きく、
# 年齢が40以上で未婚なら最終来店日からの日数の係数が負の方向に大きいはず
indivisual_summary_plot(train_df, democols, indivisual_count, indivisual_amount, indivisual_last_visit)

購入回数は女性で学生のケースが一番ランダム係数の平均値が正の方向に大きい。
購入金額は男性でProfessionalのケースが一番ランダム係数の平均値が正の方向に大きい。
最終来店日からの日数は年齢が40以上で未婚のケースが一番ランダム係数の平均値が負の方向大きい。
ということでデータ作成時の設定どおりの結果が出たのではないだろうか。

予測サンプル生成（テストデータ）

一応、未知データとしてテストデータの推論もしておく。
pm.set_dataでテストデータの情報に更新した後に、pm.sample_posterior_predictive()で予測を行う。
テストデータはf1_score 0.79と、まあぼちぼちの結果。

# テストデータの推論
with model_random3:
    pm.set_data({'demo_x':test_df[democols].to_numpy()
                 , 'purchase_x':test_df[purchasecols].to_numpy()
                 , 'y': np.zeros(len(test_df[purchasecols].to_numpy()))  # yは未知とする。実際の答えはtest_df['purchase'].to_numpy()。
                }
                , coords={"data": (np.arange(test_df.shape[0]))+train_df.shape[0]}
               )
    trace.extend(pm.sample_posterior_predictive(trace))

# テストデータを使って予測
p_preds_test = trace.posterior_predictive["obs"].mean(dim=["chain"]).values  # chain平均
p_pred_test = trace.posterior_predictive["obs"].mean(dim=["chain", "draw"]).values  # chainとサンプル平均
y_pred_test = (p_pred_test >= 0.5).astype("int")  # 0.5以上を1
y_true_test = test_df['purchase'].to_numpy()  # 実際の購買有無
p_true_test = test_df['probabilities'].to_numpy()
result_summary(p_true_test, p_pred_test, y_true_test, y_pred_test)

• 評価指標（テストデータ）
  accuracy_score 0.9264305177111717
precision_score 0.8225806451612904
recall_score 0.7611940298507462
f1_score 0.7906976744186047

• 混同行列（テストデータ）
  
  （他指標は省略）

おわりに

今回作ったすべてのモデルは精度的にはおおよそ同じくらいかな。
ただベイズモデルの方が解釈できる幅が広い。各個人それぞれで変数の影響を見れるので、例えばOne-To-Oneで何かしら施策をしたりアプローチできるのは非常に良いことなのではなかろうか。
今回は2値分類としてロジスティック回帰をベースに実践してみたが、分類ではなく回帰なら線形回帰やポアソン回帰で同様のことができる。
一般化線形モデルの枠組みだけでなく階層構造も含めて柔軟にモデルを組むことができるので、使いこなすことができればかなり強力なツールになると思った。ただ事前分布をどう設定すべきなのかとかわかっていないことも多いのでもっと勉強が必要だなぁ。

以上！

おまけ

LightGBMで全部の変数突っ込んで精度見てみた。

# LightGBMデータセットを作成
X_train = train_df[purchasecols+democols]
y_train = train_df['purchase'].astype(int)
X_test = test_df[purchasecols+democols]
y_true_test = test_df['purchase'].astype(int).to_numpy()
train_data = lgb.Dataset(X_train, label=y_train)

# LightGBMハイパーパラメータの設定
params = {
    'objective': 'binary',
    'boosting_type': 'gbdt',
    'metric':'binary_logloss',
    #'learning_rate': 0.05,
    #'num_boost_round': 300
}

# モデルの訓練
modellgb = lgb.train(params, train_data)

テストデータの精度確認。

# テストデータを使って予測
p_pred_test = modellgb.predict(X_test)
y_pred_test = (p_pred_test >= 0.5).astype("int")  # 0.5以上を1
y_true_test = test_df['purchase'].to_numpy()  # 実際の購買有無
p_true_test = test_df['probabilities'].to_numpy()
result_summary(p_true_test, p_pred_test, y_true_test, y_pred_test)

• 評価指標（テストデータ）
  accuracy_score 0.9291553133514986
precision_score 0.8253968253968254
recall_score 0.7761194029850746
f1_score 0.8

• 混同行列（テストデータ）
  
  （他指標は省略）

f1_score 0.8なので精度としては一番良い。でも解釈性を考えると実務では階層ベイズの方が良い場面はいっぱいありそう。