東京大学空間情報科学研究センター・株式会社Nospareの菅澤です.
今回は最近の研究成果「ロバストなベイズ的回帰分析のための新しい誤差分布」について紹介いたします.
ロバストなベイズ的回帰分析
モデルの仮定から大きく逸脱したデータのことを一般的に外れ値と言います.多くの統計手法は外れ値に大きな影響を受けてしまうことが知られており,推定結果に深刻なバイアスが生じる危険性があります.
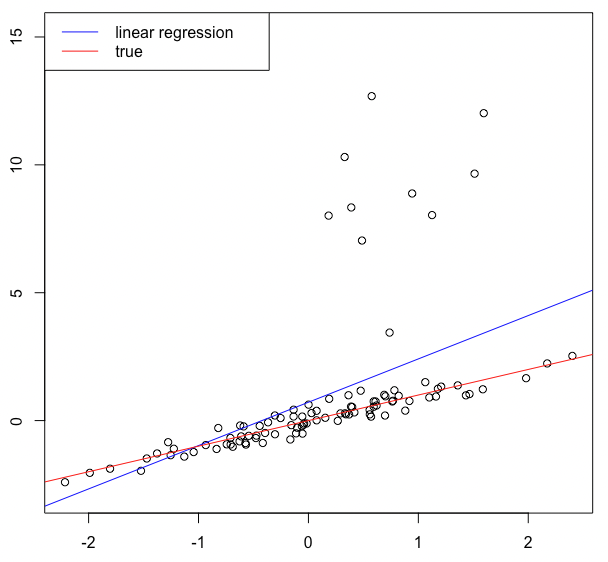
簡単な例として以下のような回帰分析の例を考えてみます.(データは擬似的により生成したものです.)
上図では赤線が真の回帰直線を表します.青線が通常の線形回帰分析によって推定された直線ですが,右上部にある外れ値らしきデータに影響を受けて真の傾きよりも大きい値が推定されてしまっています.
この場合の簡単な対処法としては外れ値らしきデータを取り除いてから解析をすることですが,外れ値の特定は必ずしも容易ではありません.今回のようにデータを図示できる場合は視覚的に外れ値を見つけられる可能性がありますが,説明変数が複数ある一般のケースにおいて外れ値の特定は困難です.
そのため,回帰モデルのロバスト(頑健)な推定と外れ値の特定(および除去)を同時に実行するための手法が必要不可欠となります.
ベイズ的回帰分析
頻度論的アプローチによるロバストな手法についてはさまざまな研究の蓄積があります.一方で,ベイズ的な推定を考えた場合,推定結果の不確実性評価が容易であったり,より複雑な統計モデルへの拡張が容易であるなど,さまざまなメリットがあります.そこで,本研究では外れ値がある場合のロバストなベイズ的回帰分析に注目していきます.
以下の(線形)回帰モデルを考えます.
$$
y_i=x_i^t\beta + \sigma\varepsilon_i, \ \ \varepsilon_i\sim N(0,1), \ \ \ \ i=1,\ldots,n.
$$
ここで$y_i$は応答変数(response variable),$x_i$は共変量(covariate)ベクトルです.また,$\sigma$は誤差項の標準偏差です.このモデルの仮定のもと,$(\beta,\sigma)$に対する適当な事前分布を導入することで,$(\beta, \sigma)$の事後分布を導出することができます.
しかし,誤差項に対する正規分布の仮定は外れ値の影響を受けやすいことが知られています.広く用いられている改善策としては標準正規分布の代わりにt分布を利用するものがあります.$t$分布は正規分布よりも裾が重いため外れ値の影響を受けにくくなります.
一方で,$t$分布は"自由度"と呼ばれるパラメータを持っており,実際に回帰モデルを推定する際にはその自由度パラメータを決定する必要があります.
- どのような自由度を具体的に設定するべきなのか
- どのような意味で外れ値の影響を受けにくくなるのか
についてはあまり明らかにされておりません.
そこで本研究では,ベイズ分析が外れ値に対して頑健であることを定義し,それを達成するために有効な誤差分布をデザインすることを目指しました.
"自由度0のt分布"の誤差分布
ベイズ分析におけるロバスト性
$D$を観測データの集合とし,$D^{\ast}$を外れ値を含まないデータの集合と定義します.(もちろん$D^{\ast}$がどのような集合になるかについて我々は知ることができません.) また,それぞれのデータに基づく事後分布をそれぞれ$\pi(\beta, \sigma|D)$, $\pi(\beta, \sigma|D^{\ast})$と定義しておきます.
本論文では,ベイズ分析におけるロバスト性として以下のような定義を採用しました.
外れ値が回帰直線から離れていくにつれ,$\pi(\beta, \sigma|D)$が$\pi(\beta, \sigma|D^{\ast})$に収束する
これは,どのデータが外れ値かを自動的に検出し,その情報を事後分布から取り除くことが可能であることを示唆しています.すなわち,外れ値でないデータだけを自動的に集めて事後分布を計算できていることを表しています.
新しい誤差分布
本研究では新しい誤差分布として以下のような分布を提案しました.
f_{\rm EH}(\varepsilon_i)=(1-s)\phi(\varepsilon_i; 0,1) + s\int_0^{\infty}\phi(\varepsilon_i;0,u_i)H(u_i;\gamma),\\
H(u_i;\gamma)=\frac{\gamma}{1+u_i}\frac{1}{\{1+\log(1+u_i)\}^{1+\gamma}}, \ \ \ u_i>0.
ただし,$\phi(\cdot; 0,u)$は平均$0$,分散$u$の正規分布の密度関数を表します.また$s$は未知の混合パラメータで,$\gamma$は形状パラメータです.上記の分布では,第一項は通常の正規分布になっている一方で,第二項が非常に裾の厚い分布になっており,外れ値の影響を吸収するための分布になっています.
提案分布の具体的な裾の厚さについては,十分大きな$|x|$に対して
f_{\rm EH}(x)\approx |x|^{-1}(\log|x|)^{-1-\gamma}
となります.したがって対数項を無視すれば,提案分布の裾はほぼ**"自由度0のt分布"と同等になることがわかります.このような性質を鑑みて,提案分布をextremely heavy-tailed (EH) 分布**と呼ぶことにします.
理論的な性質
EH分布を誤差分布として用いた回帰モデルに対する理論的結果として,
- 上で定義した事後分布のロバスト性が成り立つことを示しました.(EH分布を用いた事後分布では外れ値が自動的に無視される.)
- 自由度が正のt分布を用いた場合,事後分布のロバスト性が成り立たないことを示しました.
2番目の結果は,応用上頻繁に用いられる$t$分布では事後分布のロバスト性を達成することはできず,外れ値の構造によっては誤った分析結果が得られてしまう可能性があることを示唆しています.
効率的な計算手法
ベイズ分析ではマルコフ連鎖モンテカルロ(MCMC)法と呼ばれるシミュレーション技術を用いて事後分布から乱数を生成することで統計的推測を行うのが一般的です.その際に MCMCがどの程度効率的に実行できるかが重要なポイントとなります.
アルゴリズム的側面における本研究の貢献として,EH分布を用いた場合の効率的なMCMCアルゴリズムを開発しました.その基礎となるのが以下の階層表現(積分表現)です.
u_i|v_i \sim {\rm Ga}(1, v_i), \ \ \ v_i|w_i\sim {\rm Ga}(w_i, 1), \ \ \ w_i\sim {\rm Ga}(\gamma,1).
ここで,$v_i$および$w_i$は効率的なMCMC法を導出するために補助的に導入する変数です.
上記の表現から$u_i$の周辺分布を求めるとその密度関数は$H(u_i;\gamma)$になります.
このような階層表現と有限混合モデルの階層表現を組み合わせることで,EH分布を誤差分布にもつ回帰モデルに対して簡単なギブスサンプリングによるMCMC法を導出することができます.
また,このような効率的な計算アルゴリズムは線形回帰モデルに限らず,正規分布をベースにした統計モデル全般に適用することができます.論文中では,線形回帰モデルだけでなく線形混合モデルや空間回帰モデルに適用した事例も紹介しています.
まとめ
本研究では,ベイズ統計学の枠組みで外れ値を処理するための新しい誤差分布を開発しました.提案分布は強力なロバスト性をもつ望ましい分布であるだけでなく,正規分布をベースにしたモデルに容易に組み込むことができるため,単純な線形回帰モデルだけでなく,状態空間モデルなどのより複雑なモデルにも組み込むことが可能です.今後は理論・応用ともにそのような方向性で研究を進めていこうと考えています.
今回の研究の詳しい内容については以下の論文をご参照ください.
Hamura, H., Irie, K. and Sugasawa, S. (2020). Log-regularly varying scale mixture of normals for robust regression. arXiv:2005.02800 (現在査読付国際誌にて審査中)
また提案手法を実装したRコードはGitHubのページ から入手することができます.(詳しくはこちらのR編で紹介しています.)
応用可能性のある分野
外れ値の問題をベイズ統計学の枠組みで扱うことで,事後的にそれぞれのデータに対して「外れ値である確率」を算出することが可能です.このような情報は
- おとり不動産物件の検出
- プラントの異常値検出
- 不正会計の自動検知
など様々な応用分野で有益であると考えられます.
今回の内容に関連する共同研究・各種お問い合わせにつきましては,お気軽に菅澤までご連絡ください。
また,株式会社Nospareではロバストなベイズ分析に限らず,統計学の様々な分野を専門とする研究者が所属しております.統計アドバイザリーやビジネスデータの分析につきましては株式会社Nospareまでお問い合わせください.