東京大学空間情報科学センター・株式会社Nospareの菅澤です.
今回は「ロバストなベイズ的回帰分析のための新しい誤差分布(理論編)」で紹介した手法をRで利用する方法について紹介します.
R関数のダウンロード
提案手法を実行するR関数はこちらのGitHubのページからダウンロードできます.今回はその中で提案したEH分布を線形回帰モデルに組み込んだEHE-LM-Function.Rを使います.
提案したEH分布のもとで基本的な回帰分析を実行する関数がEHE()関数です.重要な引数としては
-
Y: 線形回帰モデルにおける応答変数のベクトル -
X: 線形回帰モデルにおける説明変数の行列 (切片項は含めない) -
mc: MCMCの総繰り返し数 -
burn: 収束までの期間として捨てるサンプル数
mcからburnを引いた数が関数から返ってくる事後分布のサンプル数になります.
使ってみる
人工的なデータを以下から生成します.
y_i=\beta_0 + \sum_{k=1}^{20}\beta_kx_{ik}+\sigma\varepsilon_i, \ \ \ \ \ \ i=1,\ldots,200, \\ \varepsilon_i\sim (1-\omega)N(0,1) + \omega N(\mu ,1).
ただし,今回は$\omega=0.1, \mu=10, \sigma=0.5$と設定します.
(約10%程度回帰直線よりも極端に大きな値を持つ外れ値が混入する設定です.)
また回帰係数については$\beta_0=0.5, \beta_1=\beta_4=0.3, \beta_7=\beta_{10}=2$とし,残りは全て0にします.
以下,データを生成するコードです.
source("EHE-LM-Function.R")
set.seed(1234)
# 設定
p <- 20 # 説明変数の数
n <- 300 # データの数
aa <- 10
om <- 0.1
sigma <- 1
# 回帰係数ベクトルの設定
Beta <- rep(0,p)
Beta[c(1,4,7,10)] <- c(0.3, 0.3, 2, 2)
int <- 0.5 # 切片項
# 説明変数行列の生成
rho <- 0.2
mat <- matrix(NA,p,p)
for(k in 1:p){
for(j in 1:p){ mat[k,j] <- rho^(abs(k-j)) }
}
X <- mvrnorm(n, rep(0, p), mat)
# 応答変数ベクトルの生成
ch <- rbinom(n, 1, om)
noise <- (1-ch)*rnorm(n, 0, 1) + ch*rnorm(n, aa, 1)
Y <- int + as.vector(X%*%Beta) + sigma*noise
このデータに対してEHE()関数を適用してみます.
またEHE-LM-Function.Rの中には通常の正規分布を用いた線形回帰モデルのコードもBR()関数として含まれているので,比較のためこちらも適用してみます.
# 関数の適用
fit.EHE <- EHE(Y, X, mc=3000, burn=1000) # EH分布 (提案手法)
fit.N <- BR(Y, X, mc=3000, burn=1000) # 正規分布
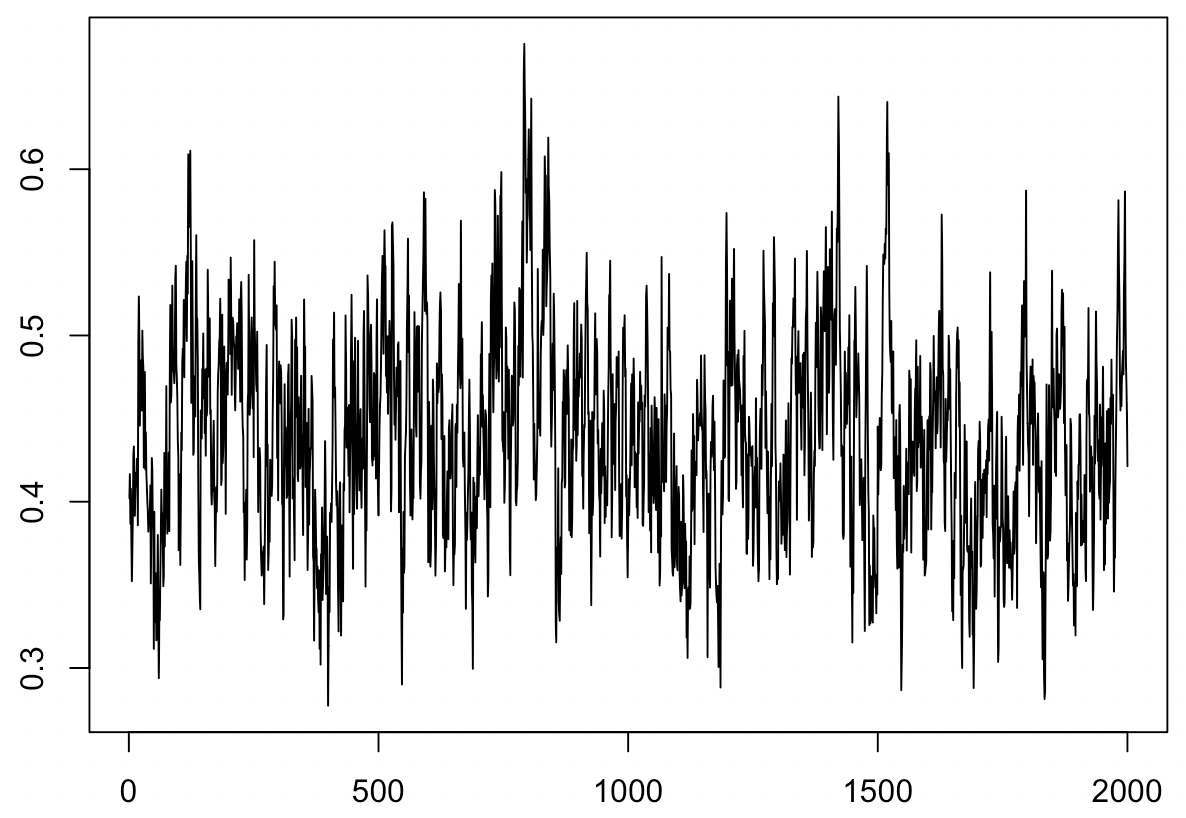
EH分布を用いた際の$\omega$の事後分布のサンプルパスは以下のようになります.
MCMCの各繰り返しで$\omega$の値がゼロより大きな値を取っているので,データに外れ値が含まれていることが示唆されています.
次に事後平均を計算し,真値との誤差を計算してみます.
# 事後平均
est.EHE <- apply(fit.EHE$Beta, 2, mean)
est.N <- apply(fit.N$Beta, 2, mean)
# 事後平均と真値の二乗誤差
Para <- c(int, Beta)
sqrt(mean((est.EHE-Para)^2)) # 結果: 0.071
sqrt(mean((est.N-Para)^2)) # 結果: 0.326
この結果から,EH分布を用いたモデルの方が正規分布を用いたモデルと比べて精度の高い点推定値を与えていることがわかります.
回帰係数の95%信用区間は以下のように計算できます.
CI95 <- function(x){ quantile(x, prob=c(0.025, 0.975)) }
CI.EHE <- apply(fit.EHE$Beta, 2, CI95)
CI.N <- apply(fit.N$Beta, 2, CI95)
最後に,回帰係数の真値と事後平均,95%信用区間の結果を可視化します.
plot(Beta, pch=4, lwd=2, ylim=range(CI.N), xlab="covariate index", ylab="coefficient", main="")
points(cbind((1:p)-0.1, est.EHE[-1]), col=2, pch=20)
points(cbind((1:p)+0.1, est.N[-1]), col=4, pch=20)
for(k in 1:p){
lines(rep(k-0.1, 2), CI.EHE[,k+1], col=2)
lines(rep(k+0.1, 2), CI.N[,k+1], col=4)
}
legend("topright", legend=c("EH", "N"), col=c(2,4), lty=1, pch=20)
上図で"EH"はEH分布、"N"は正規分布を誤差分布として用いたことを表します.また図中の"×"は真値に対応します.この結果から,外れ値がデータに含まれる状況において,EH分布は正規分布よりも
- 事後平均の推定精度が高く
- より範囲の狭い(効率的な)信用区間を得られる
ことが観察できます.
このように,外れ値があるにも関わらずEH分布が精度の高い推定結果を出せるのは,EH分布のもつ"事後分布のロバスト性"に由来していると考えられます.
まとめ
今回は線形回帰モデルにおけるEH分布の利用について紹介しましたが,GitHubのページでは,線形混合モデル(ランダム切片モデル)および空間回帰モデルに関するコードもアップしておりますので,ご興味がある方は試していただけますと幸いです.
より詳しい方法論については以下の原論文に記載されております.
Hamura, H., Irie, K. and Sugasawa, S. (2020). Log-regularly varying scale mixture of normals for robust regression. arXiv:2005.02800
今回の内容に関連する共同研究・各種お問い合わせにつきましては,お気軽に菅澤までご連絡ください。
また,株式会社Nospareではロバストなベイズ分析に限らず,統計学の様々な分野を専門とする研究者が所属しております.統計アドバイザリーやビジネスデータの分析につきましては株式会社Nospareまでお問い合わせください.