学習効果を統計的に評価したい!
こんにちは![]()
グロービスではさまざまな教育事業を展開していますが、多くの人に学習を継続してもらうためには、研修をしたりコンテンツを視聴してもらったりするだけでなく、その学習効果を測定してユーザーにフィードバックすることが重要です。このとき、だれが見ても明らかな効果が出れば良いのですが、受講前後の成績変化のばらつきが大きかったりデータが少なかったりして、必ずしも分かりやすい結果が得られるとは限りません。そういった場合にデータを丁寧に紐解いて、どの程度効果があったのかを明らかにするのも分析の仕事のひとつです。
今回は階層ベイズモデルという統計モデルを使って、高校における学力コーチングの成果についてのデータを分析します。階層ベイズはやや高度な統計モデルというイメージがありますが、この記事ではたった8行のデータを例にしてその概要を説明してみたいと思います。
想定読者
- 新薬の効果、教育の効果、マーケティングの効果、筋トレの効果などを統計的に評価したいと思ったことがある人
- 階層ベイズという言葉をどこかで聞いたことがあるけれどそれが何なのかは分からない人
- データサイエンティストは8行しかないデータをどう分析するのか知りたい人
前提知識としては「正規分布」という言葉を知っているくらいの読者を想定しています。
記事に書かれていないこと
- 「ベイズ」が何なのかについては説明していません。でも知らなくても読めると思います。
要約
- 8つの学校で実施された学力コーチングの効果を異なる3つの考え方で推定してみた。
- モデル1:それぞれの学校を互いに何の関係もないものとして別々に考える。
- モデル2:全校の平均だけを考慮して各学校の個別性は無視する。
- モデル3:モデル1とモデル2の中間をとって学校ごとの個別性も全体性も同時に考慮する(階層ベイズモデル)。
- $\sigma$というパラメータで個別性と全体性のバランスを調整できる。
- 「個別性と全体性のバランス」という考え方は日常のいろいろな場面に当てはめることができる。
データ(8 schools)
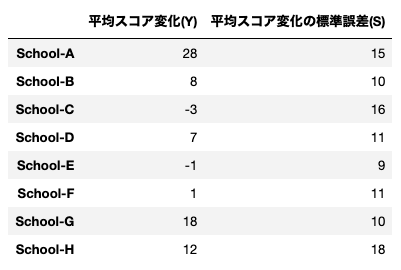
8 schools は統計学の大先生でStanという確率的プログラミング言語の開発者でもあるAndrew Gelmanによる教科書『Bayesian Data Analysis』で取り上げられているデータです。データには8つの高校で実施された標準学力テスト対策のコーチングの効果が格納されています。生徒はコーチングの前後でテストを受験しており、各校に対してコーチング前後のスコア変化の平均値と、その標準誤差(※1)が入っています。
8 schools はStanの公式チュートリアルでも使われているので見たことがある人もいるかもしれませんが、単にStanを動かすのに手ごろなサンプルというだけではなく、階層ベイズの考え方に慣れるにもうってつけのデータです。たった8行のデータで分析も何もないじゃないか?と思ってしまいますが、実は意外といろいろな見方ができます。
問題:コーチングの効果はあったのか?
このデータから知りたいことはシンプルで、**「コーチングの効果はどのくらいあったのか?」**ということです。
例えば学校Hでのコーチングの効果について考えてみます。平均では12点スコアが上昇していますが標準誤差は18点なのでスコアが下がった生徒もたくさんいるでしょう。また、他の7校のデータもありますが、学校Hにおける効果を考える上でそれらも考慮すべきでしょうか?学校Aでは28点も上がっていますし、学校Cでは逆に3点下がっています。考え出すとなかなか悩ましいですが、ひとまず次の二つの考え方で推定をしてみました。
-
学校Hの効果について知りたいのだから学校Hにおけるデータだけを考えるのが正確だろう。したがって学校Hでの効果は12点と推定するのがよい。(モデル1)
-
どの学校でも同じコーチングの内容は同じなのだからなるべく多くのデータを考慮するのが正確だろう。したがって学校Hでの効果は全学校の平均で約7.7点(※2)と推定するのがよい。(モデル2)
確率モデル
先ほどの二つのモデルを数式で表してみましょう。
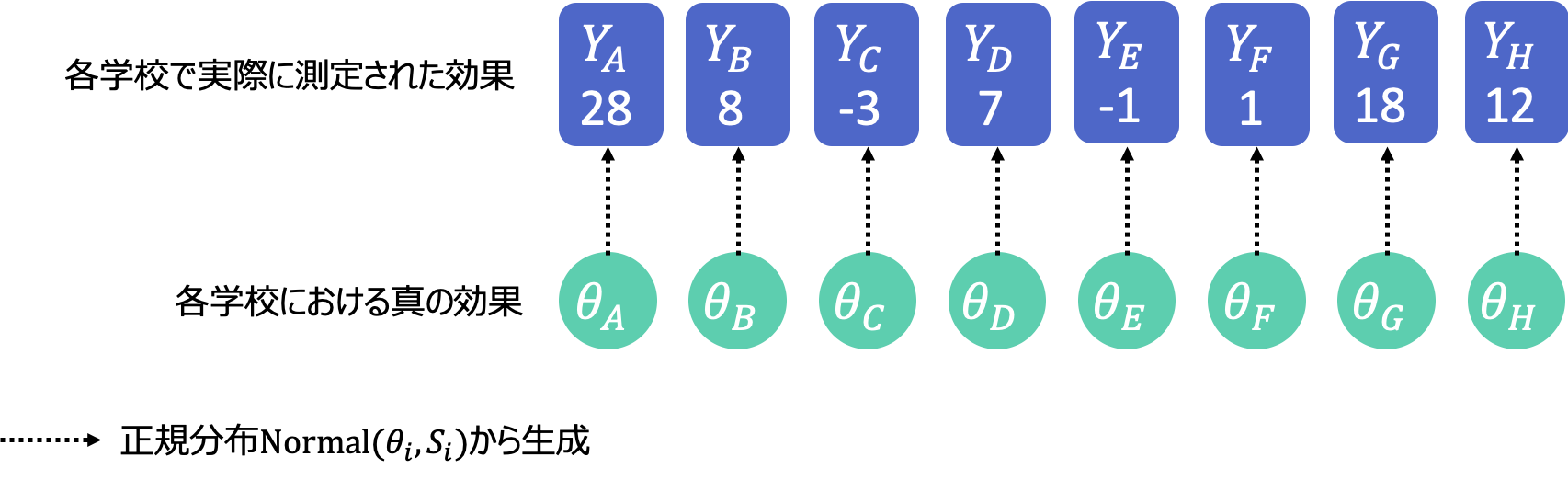
まずはモデル1です。各学校の平均スコアを$\rm{Y_i}$、標準誤差を$\rm{S_i}$、推定したい真の効果を$\rm{\theta_i}$と表記して、$\rm{Y_i}$は平均$\rm{\theta_i}$、標準偏差$\rm{S_i}$の正規分布から生成されるものとします($\rm{i}=A,B,...,H$)。ポイントは8つの$\rm{\theta_i}$を関連づけるものが何もないというところです。これによって各学校の効果はその学校のデータだけから推定するしかありません。
\rm{Y_i} \sim \rm{Normal}(\theta_i, {S_i})\tag{1}
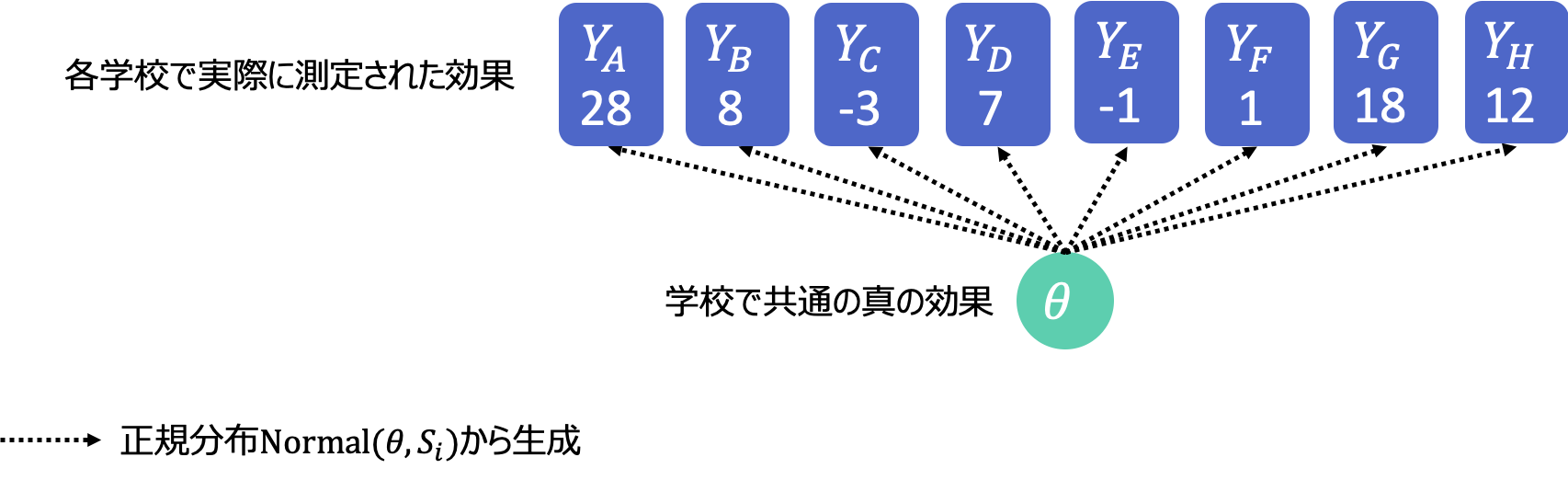
次にモデル2です。今度は学校ごとに別々ではなく、全校共通の真の効果$\rm{\theta}$が一つだけあると仮定します。そしてこの$\rm{\theta}$から8つ全ての学校のデータが生成されたと考えます。式で書くと次のようになります。先程との違いは$\rm{\theta}$の添字$\rm{i}$が無くなっただけですが、これによって全ての学校が$\rm{\theta}$という一つのパラメータを通して関連づけられました。
\rm{Y_i} \sim \rm{Normal}(\theta, {S_i})\tag{2}
階層ベイズモデル
これら二つのモデルは、どちらもある意味とても極端なデータの見方です。どういうことかというと、
-
モデル1はコーチングの内容が同じであるにもかかわらず各学校におけるコーチングの効果は完全に別々だと思ってしまって、せっかく他の学校で得られたデータを無視しています。
-
モデル2はコーチングの内容が同じだからといって全ての学校を十把一絡げにし、学校ごとの個別性を無視してしまっています。
どうにかして、この二つの中庸を行くような上手い推定をすることはできないものでしょうか?
できます![]()
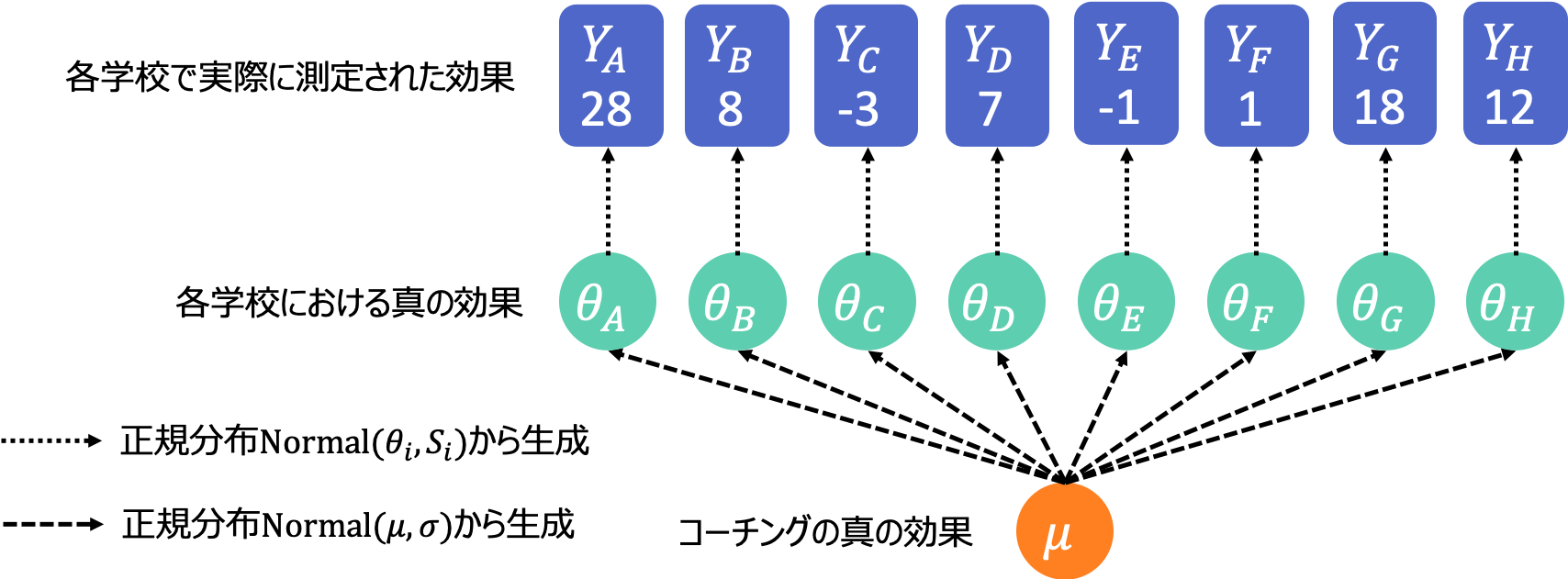
まず、どの学校に対しても共通したコーチングそのものの真の効果 $\rm{\mu}$ というものを考えます。そして学校ごとのコーチングの効果$\rm{\theta_i}$は平均 $\rm{\mu}$、標準偏差 $\sigma$ の正規分布から生成されたものだということにします。つまり、どの学校も同じコーチングをしているわけだからだいたい$\mu$くらいの効果になるでしょう、でも学校によってコーチだったり生徒だったり教室の温度だったり違いはあるだろうから、それによって$\sigma$くらいはばらつくでしょう、という風に考えているわけです。正規分布から生成されるという部分に特にこだわりはないのですが、他の確率分布を仮定するべき強い理由もないのでそうしています。これをモデル3としましょう。式で書くと次のようになります。
\rm{Y_i} \sim \rm{Normal}(\theta_i, {S_i})\\
\rm{\theta_i} \sim \rm{Normal}(\mu, {\sigma}) \tag{3}
このモデルでは$\rm{\theta_i}$というパラメータが一つ一つの学校の個別性を表しているのと同時に、各$\rm{\theta_i}$が同じ正規分布から生成されたものだと考えることで学校同士が互いに無関係ではないということを表現できています。このようなモデルを階層ベイズモデルといいます。コーチングの真の効果から各学校の効果が生成され、さらにそこから実際のデータが生成されるので「階層」という名前がついています。
ということで、個別性しか考慮しないモデル1と全体性しか考慮しないモデル2の中間のモデル3を作ることに成功しました。
個別性と全体性のバランスを決めるパラメータ
ここで突然ですが、式(3)の$\sigma$というパラメータに注目してみましょう。これは何を意味しているでしょうか?
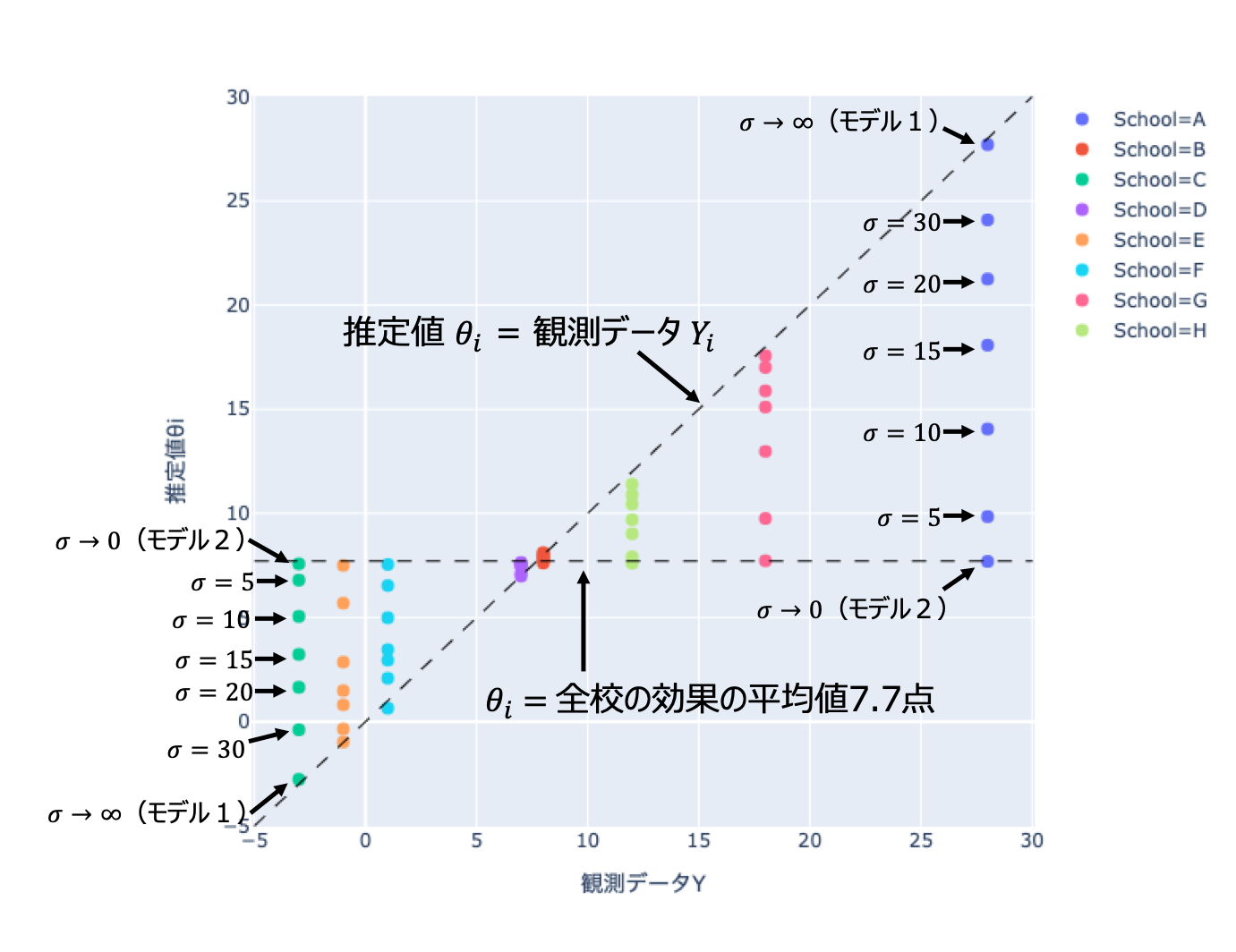
式(3)は学校ごとの真の効果$\rm{\theta_i}$が$\sigma$くらいばらつくと言っています。試しに$\sigma\to0$としてみるとどうなるでしょうか?学校間のばらつきがゼロになるわけですから、全ての学校の$\rm{\theta_i}$が同じ値になります。これは学校間の個別性を無視したモデル2と同じです。逆に$\sigma\to\infty$とするとどうでしょうか?この場合は正規分布の形が限りなく平坦になって各学校の$\rm{\theta_i}$はほとんど自由にどんな値でも取っていいことになります。これは学校間の関係性を完全に無視したモデル1と同じです。このように、$\sigma$というパラメータはモデルの全体性と個別性のバランスをコントロールしています。
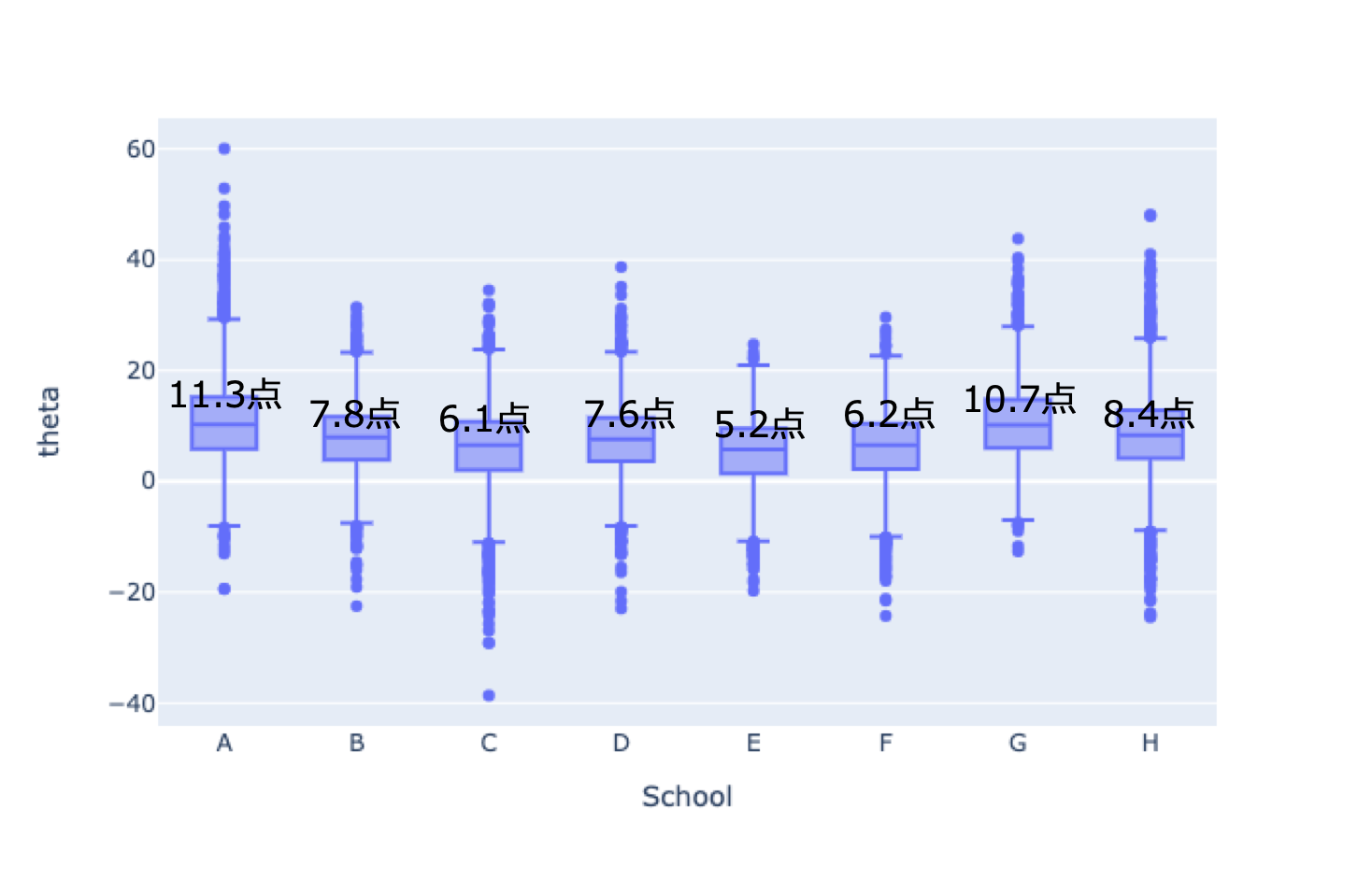
下図はモデル3でいくつかの$\sigma$の値に対して$\rm{\theta_i}$を推定した結果です。階層ベイズモデルを使うと、平均より大きな効果がデータとして得られた学校(学校A、学校Gなど)はそれより小さめに、平均より小さな効果がデータとして得られた学校(学校C、学校E)はそれより大きめに真の効果が推定されています。そのときに補正を効かせる強さを決めるのが$\sigma$というわけです。
そうすると結局どの$\sigma$を選べばいいの?という疑問が出てきます。この記事では詳しく触れませんが、$\sigma$も未知パラメータの一つとして、データに対するあてはまりが良くなるようにアルゴリズムで推定することができます。それによって、個別の学校のデータを信用し過ぎることもなく、かといって学校ごとの個別性を無視して過剰に保守的になることもなく、ちょうどいいバランスの各学校の効果$\rm{\theta_i}$が求まるのです。
下図はモデル3で$\sigma$と一緒に$\rm{\theta_i}$のパラメータを推定した結果です。学校Hの効果は$\rm{\theta_H}$=8.4点と推定されました。予想通り、データの12点よりは小さく、平均の7.7点よりは大きく、それらの中間くらいになっています。なお、$\sigma$は6.6点という推定結果でした。ちなみに、箱ひげ図で結果をプロットしていますが、ベイズ推定では各パラメータの推定値が一つだけ求まるのではなく、推定の不確定性も一緒に求めることができます。箱の範囲が狭ければ信頼性の高い推定、範囲が広ければあまり自信がない推定です。今回のようにデータが少ない場合でも推定の不確定性が分かるのはベイズ推定の利点のひとつです。
最後に
階層ベイズモデルの考え方は実際に多くの場面で応用することができます。
私が以前、不動産価格の相場を推定するアルゴリズムを設計したときには、地域や駅によって別々のモデル(個別性だけ)と、地域や駅の特徴を使わないモデル(全体性だけ)の中間で、バランスの取れた精度の良いモデルを階層ベイズで作ることができました。ランダムフォレストやニューラルネットといった比較的よく使われる機械学習のアルゴリズムだと、個別性の側に偏り過ぎたオーバーフィット気味のモデルになりがちです。
また、web広告を配信しているマーケティングの現場でも、階層ベイズの考え方を使うことができます。ある日、性別と年齢層別にセグメントを分けて広告がクリックされた数をモニタリングしていたところ、30代男性のクリック数がいつもより少し増えていました。こんなとき、「今日は調子がいいみたいだから30代男性にいつもの二倍の予算を割り当てて配信するぞー」などと早まってはいけません。その他多くのセグメントの平均がいつもと同じくらいなのであれば、それはきっとただのばらつきです。こういったケースで担当者が個別性と全体性のバランスという考え方をすることができれば、不要なオペレーションを減らして広告のパフォーマンスや運用効率を改善できるでしょう。
他にも全体と個別のバランスを意識させられるような場面は日常生活のなかでしばしば遭遇します。ちなみに、上の2つのような例をみていると、機械学習にしても人間の判断にしても、個別性の方を重視し過ぎる傾向にあるんじゃないかという気がしてきます(あくまでも主観ですが)。ここ数年世界的なベストセラーになっている『FACTFULNESS』という本の第5章『過大視本能 「目の前の数字がいちばん重要だ」という思い込み』も是非読んでみることをオススメします。この記事を読んだ方が何かのデータを元に意思決定をするときに「目の前のデータに判断が引っ張られ過ぎていないかな?」と立ち止まって考えるきっかけになれば嬉しく思います(自戒を込めて)。
脚注
※1)スコアの平均値はばらつきます。今回は各学校で一回ずつしかデータを取っていませんが、もし仮に何度も調査ができるのだとしたらその度に結果は異なるでしょう。一般的に、調査対象となる生徒数が少なければそのばらつきは大きくなり、生徒数が多ければばらつきは小さくなるはずです。標準誤差はそのばらつきの程度を表したものです。標準誤差が大きい学校Hは生徒数が少なく、標準誤差が小さい学校Eは生徒数が多いと推察されます。大雑把にいうと、10回中7回くらいは平均値±標準誤差の範囲内に入る程度のばらつき、と思っておいてください。
※2)学校ごとに生徒数が異なるので平均スコア変化(Y)の平均を単純に計算するのではなく、標準誤差(S)の二乗の逆数で重み付けして期待値を計算しました。