混合ガウス分布でEMアルゴリズム実装【C++】

0. はじめに

前回の記事でEMアルゴリズムについて説明したので、C++で実装します。前回同様この記事はパターン認識と機械学習(PRML)の内容に従いますが、この本を読んでいなくても理解できるようにしています。

また、筆者はC++初心者のためコードには見苦しい点が多々あるかと思いますがご容赦ください。ずぶの素人でも作れるくらい簡単に実装できるアルゴリズムであると理解してください。他に致命的な誤り等ありましたらご指摘いただけますと幸いです。

1. EMアルゴリズム

前回の記事で詳述したので細かい説明は行いませんが、以下のEステップとMステップの処理を交互に繰り返すことで尤度関数を最大化します。

1.1 初期値の設定

$K$個のガウス分布で$N$個のデータ点$x_1, x_2, ..., x_n$が表現するデータ分布を近似するとして、$x_n$に対する分布$p(x_n)$を次で定義します。

p(x_n)=\sum_{k=1}^{K}\pi_k \mathcal{N}(x_n|\mu_k, \Sigma_k) 

初期状態としては、適当な混合係数$\pi_k$(スカラー)、平均$\mu_k$($D$次元ベクトル)、分散$\Sigma_k$($D\times D$行列)を設定します。

1.2 Eステップ

各点には各ガウス分布ごとに潜在変数の負担率$\gamma(z_{nk})$が設定されており、

\gamma(z_{nk}) = \frac{\pi_k \mathcal{N}(x_n|\mu_k, \Sigma_k)}{\sum_{j=1}^{K} \pi_j\mathcal{N}(x_n|\mu_j,\Sigma_j)}  \tag{1.1}

を計算します。

1.3 Mステップ

以下に従って各パラメータを更新します。

N_k = \sum_{n=1}^{N}\gamma(z_{nk})   \tag{1.2}

\pi_k = \frac{N_k}{N}  \tag{1.3} \\

\mu_k = \frac{1}{N_k}\sum_{n=1}^{N}\gamma(z_{nk})x_n \tag{1.4}\\

\Sigma_k = \frac{1}{N_k}\sum_{n=1}^{N}\gamma(z_{nk})(x_n-\mu_k)(x_n-\mu_k)^T  \tag{1.5}

1.2に戻って以降E及びMステップを繰り返します。

1.4 収束性の判定

以下の対数尤度が収束したらプログラムを終了します。

\ln p(X|\theta) = \sum_{n=1}^{N}\ln \bigg( \sum_{k=1}^{K}\pi_k \mathcal{N}(x_n|\mu_k, \Sigma_k)\bigg) \tag{1.6}

2. 変数の定義

以下のように各変数を定義します。

    int column_num; //データの次元数D                                                                              
    int cluster_num; //クラスタ数K                                                                            
    int data_num;//データ点の数N                                                                                         
    vector<vector<double>> mu; //K x D　D次元平均ベクトルμがK種類連なる行列                                                                                  
    vector<vector<vector<double>>> sigma; //K x D x D  DｘD共分散行列ΣがK種類連なる行列                                                                 
    vector<double> pi; //K 混合係数πがK種類連なる                                                     
    vector<vector<double>> gamma; // N x K 負担率γ                                             
    vector<double> N;　//データ数N                                                                                        
    vector<vector<double>> data; // D x N D次元ベクトルx_nがN個連なるデータX   

3. 各ステップの実装

各ステップごとに実装を進めていきます。なお、本記事では以前筆者が自分で実装した行列演算クラス、ガウス分布計算クラスを使用しますが、基本的に既存の行列計算ライブラリ等でも同様の処理となるため行列計算の部分で既存のライブラリを使用する場合は適宜読み替えていけば良いと思います。

3.1 EMクラスの宣言

今回使用するクラスをEMクラスとして次のように宣言します。なお、実際には下に宣言されている以外の関数等も出てきますが今はここで理解しておくべき関数や変数のみ記述します。（完全なコードはこの記事の末尾に載せます。）

class EM{
  public:
    int column_num; //データの次元数D                                                                              
    int cluster_num; //クラスタ数K                                                                            
    int data_num;//データ点の数N                                                                                         
    vector<vector<double>> mu; //K x D　D次元平均ベクトルμがK種類連なる行列                                                                                  
    vector<vector<vector<double>>> sigma; //K x D x D  DｘD共分散行列ΣがK種類連なる行列                                                                 
    vector<double> pi; //K 混合係数πがK種類連なる                                                     
    vector<vector<double>> gamma; // N x K 負担率γ(z_{nk})                                           
    vector<double> N;　//データ数N                                                                                        
    vector<vector<double>> data; // D x N D次元ベクトルx_nがN個連なるデータX                                                                       
    EM(const char filename[], int n=300, int m=2, int k=2); //初期化用コンストラクタ
    void E_step(); //Eステップ
    void M_step(); //Mステップ
    double loglikelihood(); //対数尤度計算（収束判定で使用）                                                    
};

3.2 初期化

$\mu_k$はランダムに、$\Sigma_k$は単位行列、$\pi_k$は$\frac{1}{K}$で初期化します。
コンストラクタを次のように実装します。

M::EM(const char filename[], int n, int m, int k){
  //定数初期化
  column_num = m;
  cluster_num = k;

  //データ初期化
  data.resize(m, vector<double>(n,-1)); //-1で初期化                                                                    

  //平均mu初期化
  mu.resize(cluster_num, vector<double>(column_num,-1));
  for(int i=0;i<cluster_num;i++){
    mu[i] = get_randmu();
  }

  //共分散行列Sigma初期化
  sigma.resize(cluster_num, vector<vector<double>> (column_num,vector<double>(column_num,0)));
  for(int i=0;i<cluster_num;i++){
    for(int j=0;j<column_num;j++){
      sigma[i][j][j] = 1.0; //単位行列にする                                                                            
    }
  }

  //混合係数pi初期化
  pi.resize(cluster_num, 1.0/ (double)cluster_num);

  //データ読み込み
  read_file(filename,data,column_num);
  data_num = data[0].size();

  //負担率γ初期化
  gamma.resize(data_num, vector<double>(cluster_num, 1.0/(double)cluster_num));
  
  //Nk初期化
  N.resize(cluster_num, (double)data_num / (double)cluster_num);
  update_Nk();
}

ただし、$\mu_k$の初期値を-2から+2の範囲でランダムに取得する以下の関数を利用しました。

vector<double> EM::get_randmu(){
  vector<double> t(column_num, -1);
  for(int i=0;i<column_num;i++){
    t[i] = ((double)(rand() % 100) / 100 - 0.5) * 4;
  }
  return t;
}

また、$N_k$を式(1.2)に従い取得する関数update_Nk()は下記です。

void EM::update_Nk(){
  for(int k=0;k<cluster_num;k++){
    double sum=0.0;
    for(int n=0;n<data_num;n++){
      sum += gamma[n][k];
    }
    N[k] = sum;
  }
}

またファイルを読み込む関数も使用していますが、アルゴリズムの本論と無関係のため記事末尾のコードにのみ記載します。データは読み込み時に-2〜+2の範囲に正規化しておきます。

正規化は以下の関数を使用します。

void EM::normalize(){
  int max_, min_;
  for(int i=0;i<data.size();i++){
    max_ = *max_element(data[i].begin(),data[i].end());
    min_ = *min_element(data[i].begin(),data[i].end());
    for(int j=0;j<data[i].size();j++){
      data[i][j] = ((data[i][j] - min_) / (max_ - min_) - 0.5) * 4.0; //-2~+2に正規化
    }
  }
}

3.3 Eステップ

Eステップは次のように実装しました。

void EM::E_step(){
  double sum;
  for(int n=0;n<data_num;n++){
    sum = 0.0;
    vector<double> new_vec(column_num,0);
    for(int l=0;l<column_num;l++){
      new_vec[l] = data[l][n];                                                                         
    }
    
    //式(1.1)分母計算
    for(int j=0;j<cluster_num;j++){
      sum += pi[j] * Distributions::gauss(vec2Ma(new_vec),vec2Ma(mu[j]),(Ma)sigma[j]);
    }

    //式(1.1)全体計算
    for(int k=0;k<cluster_num;k++){
      gamma[n][k] = pi[k] * Distributions::gauss(vec2Ma(new_vec),vec2Ma(mu[k]),(Ma)sigma[k]) / sum;
    }
  }
}

式(1.1)を計算するだけなのでシンプルです。ただし、ガウス分布の計算と行列計算は以前に書いた記事で実装したクラスを使用しています。

さらに、ベクトルを自分で定義したMa型に変換する関数vec2Ma()も下記で実装しました。

Ma EM::vec2Ma(vector<double> x){
  vector<vector<double>> new_x(x.size(), vector<double>(1));
  for(int i=0;i<x.size();i++){
    new_x[i][0] = x[i];
  }
  return (Ma)new_x;
}

3.4 Mステップ

Mステップは式(1.2)-(1.5)を実装します。

void EM::M_step(){
  //式(1.2)でNkを更新                                                                                                      
  update_Nk();
  
  //式(1.4)でmuを更新                                                                                                           
  for(int k=0;k<cluster_num;k++){
    for(int j=0;j<column_num;j++){
      double sum=0.0;
      for(int n=0;n<data_num;n++){
        sum += gamma[n][k] * data[j][n];
      }
      mu[k][j] = 1 / N[k] * sum;
    }
  }
  
  //式(1.5)でSigmaを更新                                                                                                        
  for(int k=0;k<cluster_num;k++){
    vector<vector<double>> A(column_num,vector<double>(column_num,0));
    vector<double> x(column_num);
    Ma sum(A);
    for(int n=0;n<data_num;n++){
      for(int l=0;l<column_num;l++){
        x[l] = data[l][n];
      }
      sum = sum + gamma[n][k] * (vec2Ma(x)-vec2Ma(mu[k])) * (vec2Ma(x)-vec2Ma(mu[k])).T();
    }
    sigma[k] = (vector<vector<double>>) (sum / N[k]);
  }
  
  //式(1.3)でpiを更新                                                                                                           
  for(int k=0;k<cluster_num;k++){
    pi[k] = N[k] / (double)data_num;
  }
}

3.5 収束性の判定

収束性判定には式(1.6)の対数尤度を計算します。今回のプログラムでは自動で収束判定する必要はないので単に毎回のループで対数尤度を計算して収束していくことを確認することとします。

double EM::loglikelihood(){
  double ll=0.0;
  for(int n=0;n<data_num;n++){
    double sum=0.0;
    vector<double>x(column_num);
    for(int j=0;j<column_num;j++){
      x[j]=data[j][n];
    }
    for(int k=0;k<cluster_num;k++){
      sum += pi[k] * Distributions::gauss(vec2Ma(x),vec2Ma(mu[k]),(Ma)sigma[k]);
    }
    ll += log(sum);
  }
  return ll;
}

3.6 その他の機能

3.6.1 パラメータの表示

パラメータの現在の値を表示するための関数です。

void EM::show_parameters(){
  cout << "data_num(N) is " << data_num << "\n";
  cout << "column_num(D) is " << column_num << "\n";
  cout << "cluster_num(K) is " << cluster_num << "\n";
  cout << "mu is \n";
                                                                                                 
  for(int i=0;i<cluster_num;i++){
    cout << "k=" << i << ":";
    cout << mu[i][0] << " " << mu[i][1] << "\n";
  }
  cout << "sigma is \n";
  for(int i=0;i<cluster_num;i++){
    cout << "k=" << i << "\n";
    cout << sigma[i][0][0] << " " << sigma[i][0][1] << "\n";
    cout << sigma[i][1][0] << " " << sigma[i][1][1] << "\n";
  }
                                                                                             
  cout << "pi is \n";
  for(int i=0;i<cluster_num;i++){
    cout << "k=" << i << ":";
    cout << pi[i] << "\n";
  }
}

3.6.2 プロットの表示

地味にプロット方法は一番苦労しました。pythonだとmatplotlibでいい感じに描画してくれますが、c++でこれに対応するような適当なライブラリが見つけられず、matplotlibのc++転用版を使用しました。

ガウス分布をプロット上でどう表現するかも難しく、pythonのように等高線を表示してくれる機能が見つけられなかったため分布上で0.05から0.06までの値を取る箇所を無理やりプロットすることでガウス分布の裾を表示することにしました。明らかにこれより良い方法がありそうです。

実装は下記です。

void EM::plot(){
  for(int k=0;k<cluster_num;k++){
    vector<vector<double>> g = get_gplots(k);
    plt::scatter(g[0],g[1]);
  }
  plt::scatter(data[0],data[1]);
  plt::xlim(-2.2,2.2);
  plt::ylim(-2.2,2.2);
  plt::show();
}

ただし、k番目のガウス分布の裾に対応する点を取得する関数get_gplots()は下記で定義します。

vector<vector<double>> EM::get_gplots(int k){
  vector<vector<double>> Gdists(column_num);
  vector<double>v(column_num);
  double threshold=0.05;                                                                                      
  for(int d=0;d<column_num;d++){
    for(double x=-2.2;x<2.2;x+=0.01){
      for(double y=-2.2;y<2.2;y+=0.01){
        v[0]=x;
	v[1]=y;
        double value = Distributions::gauss(vec2Ma(v),vec2Ma(mu[k]),(Ma)sigma[k]);
        if(value > threshold && value < threshold+0.01){
          Gdists[0].push_back(x);
          Gdists[1].push_back(y);
        }
      }
    }
  }
  return Gdists;
}

4. 実行結果

4.1 データの分布

データはPRMLでも使われているOld Faithful間欠泉データを使用します。正規化済みのデータをプロットすると下図のようになりました。

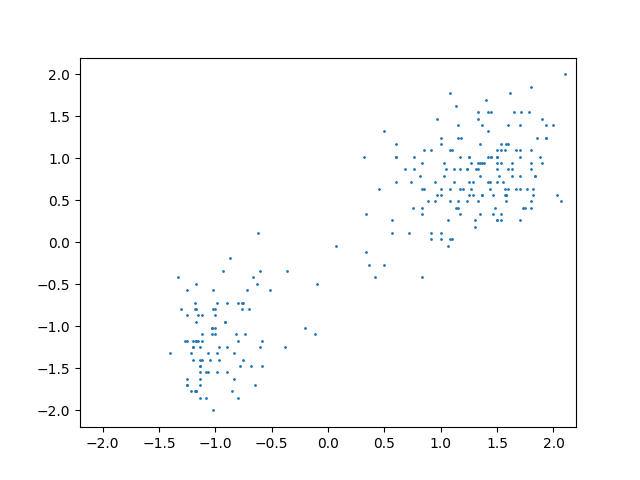
4.2 ガウス分布２つで近似

分布をみると明らかに２つのクラスタがあるので、これにクラスタ数２の混合ガウス分布で近似してみます。
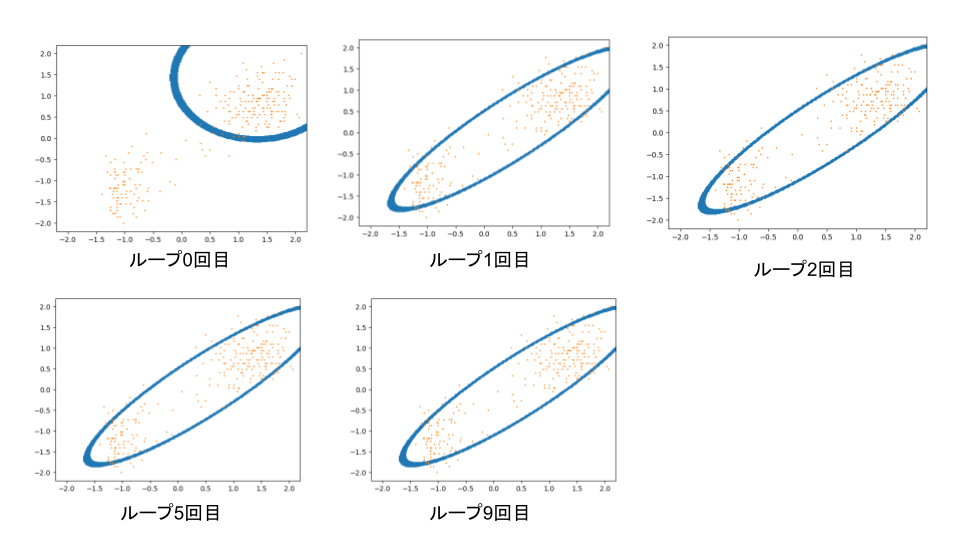
実行結果は10回ループさせた結果は下図のようになりました。

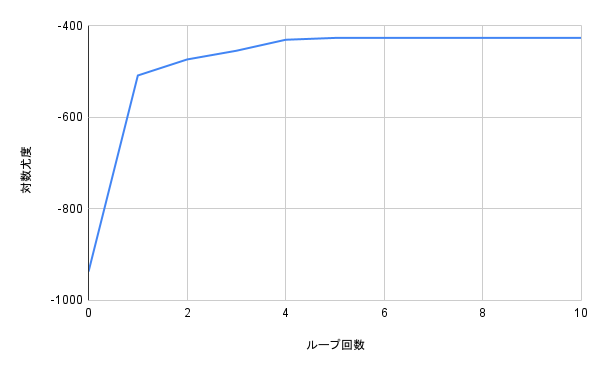
確かにランダムに設定された初期状態から徐々に２つのクラスタに分布がフィットしていっている様子が確認できます。また、このとき対数尤度は下図のように確かに上昇していることが確認できました。これを見るとループ４回目くらいから収束しきっているとわかります。

4.3 ガウス分布１つで近似

クラスタ数を１にすると単一ガウス分布となるためわざわざEMアルゴリズムを使う必要はないですが、これでもやってみます。

今度は２つのクラスタにまたがって分布が形成されることがわかりました。単一ガウス分布の場合解析的に最尤解が求まり、その平均は各データの平均、分散は各データの共分散行列の平均になるはずですが、実際そのような分布になっているように見えます。

対数尤度は下図のように１ループで収束します。

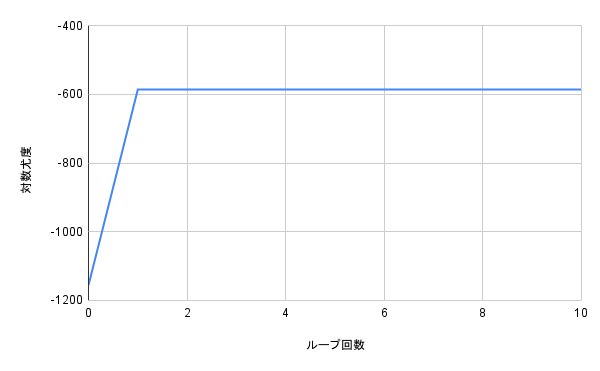
EMアルゴリズムのMステップでは前回の記事で書いたように下式の$Q(\theta, \theta^{old})$を最大化します。

Q(\theta, \theta^{old})=\sum_{Z}p(Z|X,\theta^{old})\ln p(X,Z|\theta)

１つのガウス分布だけを使う場合潜在変数は常に1となるため$p(Z|X,\theta^{old})=1$が成り立ち、よって、

Q(\theta, \theta^{old})=\ln p(X|\theta)+const.

です。つまり、Mステップで$Q$を最大化する処理は$\ln p(X|\theta)$を解析的に最大化する処理と同義となるため、解析的に最尤解が求まるクラスタ数１の条件のもとでは当然１回のループ（Mステップ処理）で最適解に収束します。

4.4 ガウス分布３つで近似

今度は本来のクラスタ数よりも多いクラス多数で近似するとどうなるでしょうか。結果は下図のようになりました。

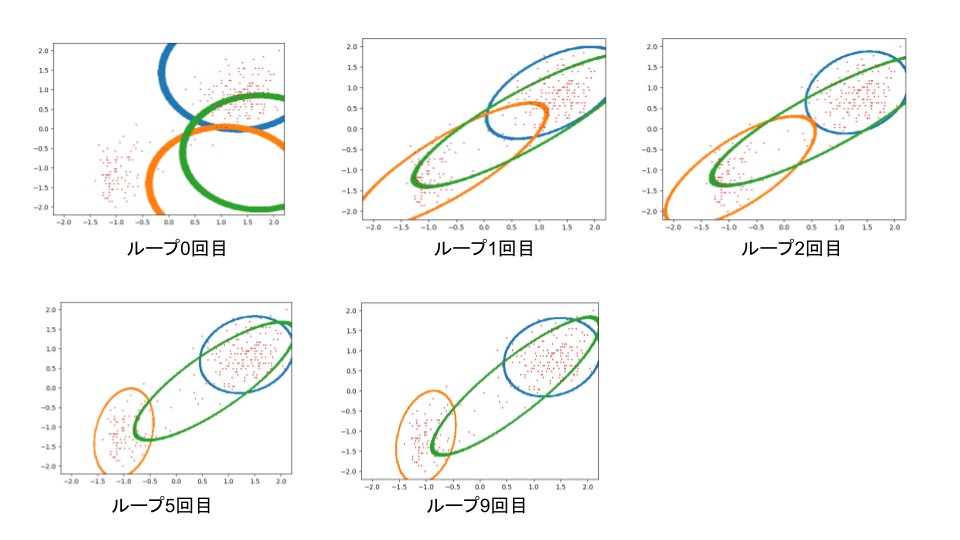
オレンジと青の分布はある程度きれいにデータを近似していますが、緑の分布が余計です。このときループ回数ごとの混合係数を計測すると、下図のようになりました。

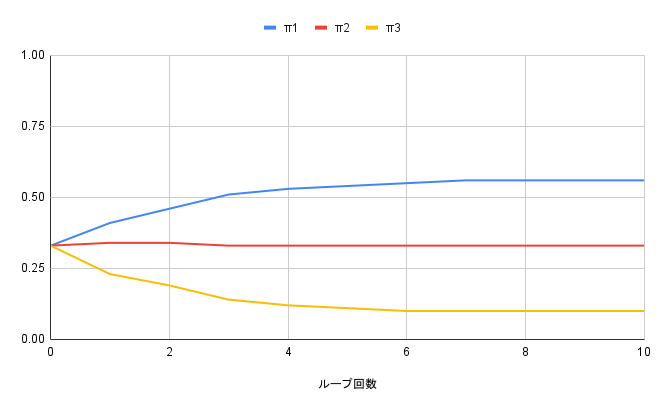
$\pi_1$が青色のガウス分布、$\pi_2$がオレンジのガウス分布、$\pi_3$が緑のガウス分布の混合係数に対応します。処理を繰り返すごとに緑のガウス分布にかかる混合係数は低く抑えられ、不必要なクラスタとして除外されるような方向に調整されていることがわかります。

また、対数尤度の変化は下のようになりました。

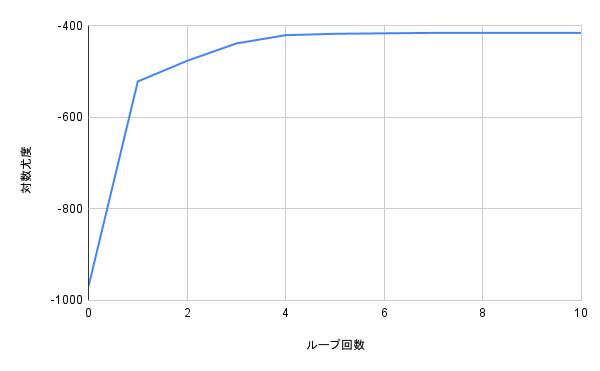
グラフだけからだと読み取りづらいですが対数尤度の最大値はクラスタ数が２だった時-427だったのに対しクラスタ数３では-416となり後者のほうがやや上回りました。しかし、クラスタ数２で最もきれいに近似できているように見えることを考えるとこれは過学習ということかと思います。

5. まとめ

以上EMアルゴリズムをC++で実装してみました。前回の記事で書いた理論が確かに正しく動作することを確かめることができました。

6. コード

em.cpp

#include "matplotlibcpp.h"
#include <random>
#include <fstream>
#include <iostream>
#include <string>
#include <sstream>
#include <vector>
#include <algorithm>
#include<Eigen/Dense>
#include "dist.h"
#include "mat.h"
using namespace std;
namespace plt = matplotlibcpp;

void read_file(const char filename[], vector<vector<double>>& data, int column_num);
class EM{
  private:
    vector<double> get_randmu();
    double gauss(vector<double> x, vector<double> mu, vector<vector<double>> sigma);
    Ma vec2Ma(vector<double> x);
    void update_Nk();
    vector<vector<double>> get_gplots(int k);
  public:
    int column_num; //column_num = D (D=2)
    int cluster_num; //cluster_num = K (K=2)
    int data_num;//data_num = N
    vector<vector<double>> mu; //K x D
    vector<vector<vector<double>>> sigma; //K x D x D
    vector<double> pi; //K
    vector<vector<double>> gamma; // N x K (N=250くらい)
    vector<double> N;
    vector<vector<double>> data; // D x N
    EM(const char filename[], int n=300, int m=2, int k=2);
    void show_data();
    void normalize();
    void show_parameters();
    void E_step();
    void M_step();
    double loglikelihood();
    void plot();
};
vector<vector<double>> EM::get_gplots(int k){
  vector<vector<double>> Gdists(column_num);
  vector<double>v(column_num);
  double threshold=0.05;
  for(int d=0;d<column_num;d++){
    for(double x=-2.2;x<2.2;x+=0.01){
      for(double y=-2.2;y<2.2;y+=0.01){
        v[0]=x;
        v[1]=y;
        double value = Distributions::gauss(vec2Ma(v),vec2Ma(mu[k]),(Ma)sigma[k]);
        if(value > threshold && value < threshold+0.01){
          Gdists[0].push_back(x);
          Gdists[1].push_back(y);
        }
      }
    }
  }
  return Gdists;
}
void EM::plot(){
  
  for(int k=0;k<cluster_num;k++){
    vector<vector<double>> g = get_gplots(k);
    plt::scatter(g[0],g[1]);
  }
  plt::scatter(data[0],data[1]);
  plt::xlim(-2.2,2.2);
  plt::ylim(-2.2,2.2);
  plt::show();
}

double EM::loglikelihood(){
  double ll=0.0;
  for(int n=0;n<data_num;n++){
    double sum=0.0;
    vector<double>x(column_num);
    for(int j=0;j<column_num;j++){
      x[j]=data[j][n];
    }
    for(int k=0;k<cluster_num;k++){
      sum += pi[k] * Distributions::gauss(vec2Ma(x),vec2Ma(mu[k]),(Ma)sigma[k]);
    }
    ll += log(sum);
  }
  return ll;
}
void EM::M_step(){
  //update Nk
  update_Nk();
  cout << "Nk is updated.\n";
  //update mu
  for(int k=0;k<cluster_num;k++){
    for(int j=0;j<column_num;j++){
      double sum=0.0;
      for(int n=0;n<data_num;n++){
        sum += gamma[n][k] * data[j][n];
      }
      mu[k][j] = 1 / N[k] * sum;
    }
  }
  cout << "mu is updated.\n";
  //update sigma
  for(int k=0;k<cluster_num;k++){
    vector<vector<double>> A(column_num,vector<double>(column_num,0));
    vector<double> x(column_num);
    Ma sum(A);
    for(int n=0;n<data_num;n++){
      for(int l=0;l<column_num;l++){
        x[l] = data[l][n];
      }
      sum = sum + gamma[n][k] * (vec2Ma(x)-vec2Ma(mu[k])) * (vec2Ma(x)-vec2Ma(mu[k])).T();
    }
    sigma[k] = (vector<vector<double>>) (sum / N[k]);
  }
  cout << "sigma is updated.\n";
  //update pi
  for(int k=0;k<cluster_num;k++){
    pi[k] = N[k] / (double)data_num;
  }
  cout << "pi is updated.\n";
}


  
void EM::update_Nk(){
  for(int k=0;k<cluster_num;k++){
    double sum=0.0;
    for(int n=0;n<data_num;n++){
      sum += gamma[n][k];
    }
    N[k] = sum;
  }
}
void EM::E_step(){
  double sum;
  for(int n=0;n<data_num;n++){
    sum = 0.0;
    vector<double> new_vec(column_num,0);
    for(int l=0;l<column_num;l++){
      new_vec[l] = data[l][n];
    }
    for(int j=0;j<cluster_num;j++){
      sum += pi[j] * Distributions::gauss(vec2Ma(new_vec),vec2Ma(mu[j]),(Ma)sigma[j]);
    }
    for(int k=0;k<cluster_num;k++){
      gamma[n][k] = pi[k] * Distributions::gauss(vec2Ma(new_vec),vec2Ma(mu[k]),(Ma)sigma[k]) / sum;
    }
  }
}
Ma EM::vec2Ma(vector<double> x){
  vector<vector<double>> new_x(x.size(), vector<double>(1));
  for(int i=0;i<x.size();i++){
    new_x[i][0] = x[i];
  }
  return (Ma)new_x;
}

void EM::normalize(){
  int max_, min_;
  for(int i=0;i<data.size();i++){
    max_ = *max_element(data[i].begin(),data[i].end());
    min_ = *min_element(data[i].begin(),data[i].end());
    for(int j=0;j<data[i].size();j++){
      data[i][j] = ((data[i][j] - min_) / (max_ - min_) - 0.5) * 4.0; //-2~+2に正規化
    }
  }
}
void EM::show_data(){
  for(int i=0;i<data.size();i++){
    for(int j=0;j<data[i].size();j++){
      cout << "data[" << i << "][" << j << "]=" << data[i][j] << "\n";
    }
  }
}
vector<double> EM::get_randmu(){
  vector<double> t(column_num, -1);
  for(int i=0;i<column_num;i++){
    t[i] = ((double)(rand() % 100) / 100 - 0.5) * 4;
  }
  return t;
}

EM::EM(const char filename[], int n, int m, int k){
  column_num = m;
  cluster_num = k;
  data.resize(m, vector<double>(n,-1)); //-1で初期化
  
  mu.resize(cluster_num, vector<double>(column_num,-1));
  for(int i=0;i<cluster_num;i++){
    mu[i] = get_randmu();
  }
  sigma.resize(cluster_num, vector<vector<double>> (column_num,vector<double>(column_num,0)));
  for(int i=0;i<cluster_num;i++){
    for(int j=0;j<column_num;j++){
      sigma[i][j][j] = 1.0; //単位行列にする
    }
  }
  pi.resize(cluster_num, 1.0/ (double)cluster_num);

  read_file(filename,data,column_num);
  data_num = data[0].size();
  gamma.resize(data_num, vector<double>(cluster_num, 1.0/(double)cluster_num));
  show_parameters();
  N.resize(cluster_num, (double)data_num / (double)cluster_num);
  update_Nk();
}
void EM::show_parameters(){
  cout << "data_num(N) is " << data_num << "\n";
  cout << "column_num(D) is " << column_num << "\n";
  cout << "cluster_num(K) is " << cluster_num << "\n";
  cout << "mu is \n";
  //print_vector(mu); 
  for(int i=0;i<cluster_num;i++){
    cout << "k=" << i << ":";
    cout << mu[i][0] << " " << mu[i][1] << "\n";
  }
  cout << "sigma is \n";
  for(int i=0;i<cluster_num;i++){
    cout << "k=" << i << "\n";
    cout << sigma[i][0][0] << " " << sigma[i][0][1] << "\n";
    cout << sigma[i][1][0] << " " << sigma[i][1][1] << "\n";
  }
  //print_vector(sigma); 
  cout << "pi is \n";
  for(int i=0;i<cluster_num;i++){
    cout << "k=" << i << ":";
    cout << pi[i] << "\n";
  }
}

void read_file(const char filename[], vector<vector<double>>& data, int column_num){
  string line,s;
  ifstream fin(filename);
  cout << data.size();

  if(!fin){
    cout << "cannot open file: " << filename << "\n";
    exit(1);
  } 
  int i=0;
  while(getline(fin, line)){
    stringstream ss{line};
    int j=0;
    while(getline(ss, s, ' ')){
      data[j][i] = stod(s);
      j++;
    }
    i++;
  }
  for(int j=0;j<column_num;j++){
    data[j].resize(i);
  }
}

int main(){
  EM em("faithful.txt",300,2,3);//em("filename",datanum,columnnum,clusternum)
  em.normalize();
  cout << "LogLikelihood=" << em.loglikelihood() << "\n";
  em.plot();
  for(int i=0;i<10;i++){
    cout << "loop" << i << "\n";
    em.E_step();
    em.M_step();
    cout << "LogLikelihood=" << em.loglikelihood() << "\n";
    em.plot();
    em.show_parameters();
  }
}