0.はじめに
EMアルゴリズムとは複雑なモデルを最適化する手法です。内容はパターン認識と機械学習の第9章に従っていますが、この本を読んでいなくても理解できるように書きます。
書籍では混合ガウス分布のEMアルゴリズムを説明してから一般化していますが、先にやろうとしていることの全体像を把握するために一般のEMアルゴリズムについて書いてから混合ガウス分布で具体化します。
C++で実装もしましたので、次の記事では実際にコード上でアルゴリズムを動かしていきます。
1.一般のEMアルゴリズムの説明
EMアルゴリズムは潜在変数を持つモデルの最尤解を求めるための方法です。潜在変数とは観測できない変数のことで、これを導入することでデータをより単純に説明することができるようになります。
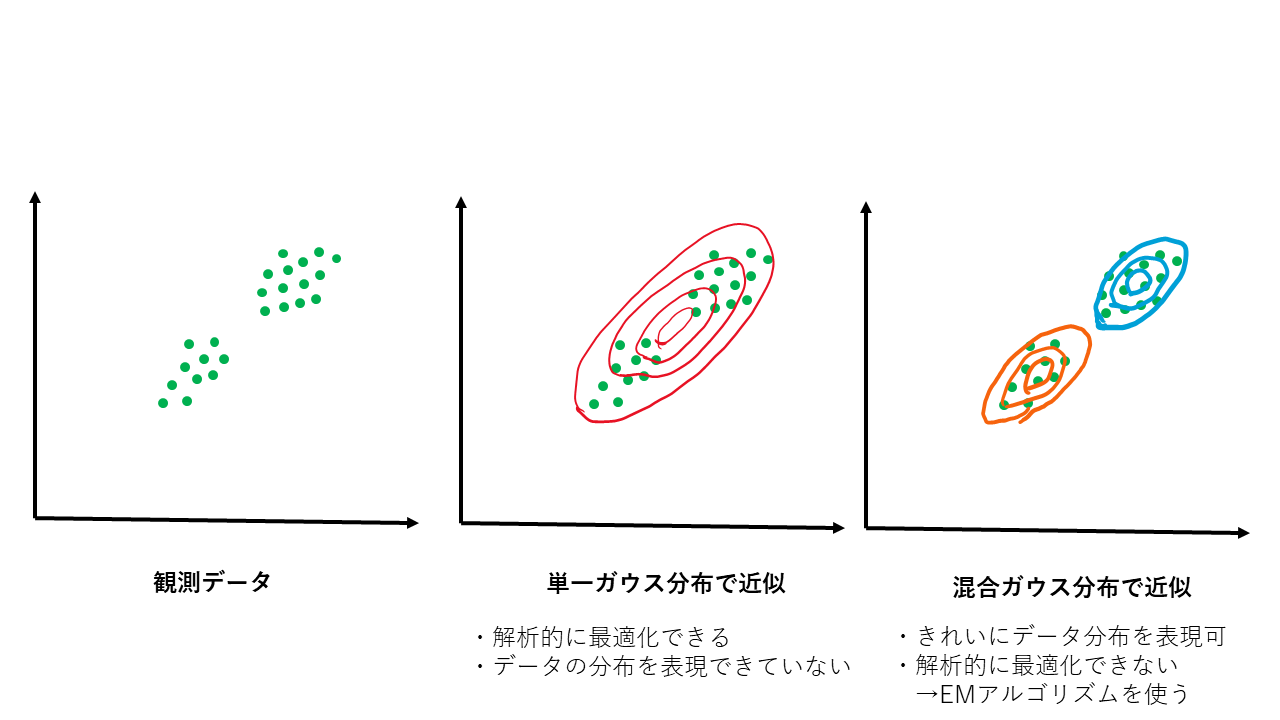
例えばランダムに日本人にメールを送り、身長を調査することを考えます。これを分布としてプロットして、ガウス分布で近似したいとします。男女の身長分布をガウス分布で表現しようとする時、1つのガウス分布だけでは男と女で別々のところにピークがあるためきれいに表現できません。2つのガウス分布で説明すればきれいに表現できるようになります。各データ点が男か女かは観測できませんが、各データ点が男である確率、女である確率を考え、男ならば男の分布、女ならば女の分布に従うとしてモデルを構築することで、データをきれいに表現できるようになるのです。この場合は性別が観測できない変数(潜在変数)です。
図で表現すると、下図の観測データのようにデータが2つのクラスタに別れる場合、単一のガウス分布ではきれいに表現しきれないデータ分布を複数のガウス分布を組み合わせることできれいに表現できるようになります。単一のガウス分布は解析的にパラメータ(=平均、分散)を最適化できますが、混合ガウス分布の場合それができないため最適な分布のパラメータを本記事で説明するEMアルゴリズムを使って最適化します。
1.1最尤推定について
まず、パラメータ$\theta$が与えられたとき、独立同分布に従って生成されたデータ点$x_1, x_2, ... x_N$に対して尤度は
p(X|\theta)=\prod_{n=1}^{N}p(x_{n}|\theta) \tag{1.1}
で与えられます。ただし$X$は$x_1, x_2,...x_N$の集合をまとめて表します。つまりパラメータ$\theta$が与えられたときに、データ$X$が得られるとしてもっともらしい確率が$p(X|\theta)$です。これを最大化するような$\theta$が得られたとすれば、それはデータに対して最も尤もらしいといえます。このため最尤推定では式(1.1)をパラメータ$\theta$に関して最大化します。
対数関数は単調増加なので式(1.1)の両辺の対数をとっても$\theta$の最大化については同じことです。対数をとると式(1.1)右辺の積計算が和計算になってくれるので計算上都合がよいため、式(1.1)両辺の対数をとってこれを最大化します。
\ln p(X|\theta)=\sum_{n=1}^{N} \ln p(x_{n}|\theta) \tag{1.2}
ここで、もし$p(x_n|\theta)=\mathcal{N}(x_n|\mu, \Sigma)$のような関数だった場合、$\ln$がかかって右辺は$\mu, \Sigma$に関する多項式になります。そのためこれらに関して式(1.2)を微分して0とおけば最適解が求まります。しかし$p(x_n|\theta)=\sum_{k=1}^{K}\pi_k\mathcal{N}(x_n|\mu_k, \Sigma_k)$のような混合ガウス分布だった場合、$\ln$の中に指数関数の和が入ってしまっているため簡単には微分して最適解を求めるというアプローチができません。
なお、$\mathcal{N}(x_n|\mu, \Sigma)$は平均$\mu$、分散$\Sigma$のガウス分布を表します。また$\pi_k$は混合係数です。
EMアルゴリズムはこのような場合に式(1.2)を最大化するパラメータ$\mu_k, \Sigma_k$を求めることができます。ただしどんな場合にもこれが適用できるというわけではなく、$X$と潜在変数$Z$の同時分布が指数型分布族であるなど、$\ln$に入れたときに簡単な分布となる場合です。これだけ書いても意味不明ですが、どういうことか以下で説明していきます。
1.2 尤度関数の変形
潜在変数$Z$と$X$の同時分布$p(X,Z|\theta)$を考えると、下記が成立します。
p(X,Z|\theta)=p(Z|X,\theta)p(X|\theta)
ただし、ベイズの定理$p(A,B)=p(A|B)p(B)$を利用しました。(参考:ベイズの定理の解説)
両辺対数をとって、
\ln p(X,Z|\theta)=\ln p(Z|X,\theta) + \ln p(X|\theta)
式(1.2)で示したように、今最大化したいのは$\ln p(X|\theta)$です。なので、上式を変形して、
\ln p(X|\theta) = \ln p(X,Z|\theta)-\ln p(Z|X,\theta) \tag{1.3}
両辺を潜在変数$Z$の分布$p(Z|X, \theta)$を近似する分布を$q(Z)$とします。式(1.3)の両辺に$q(Z)$をかけて$Z$に関して周辺化します。続けてやや天下り的な式変形ですが分布$p(Z|X,\theta)$と分布$q(Z)$の類似度を評価するKLダイバージェンス$KL(q||p)$を式中に導き出します。
\begin{align}
\sum_{Z}q(Z) \ln p(X|\theta) & = \sum_{Z} q(Z)\ln p(X,Z|\theta) - \sum_{Z} q(Z) \ln p(Z|X. \theta) \\
& = \sum_{Z} q(Z)\ln p(X,Z|\theta) +\sum_{Z} q(Z) \ln q(Z) - \sum_{Z} q(Z) \ln q(Z) - \sum_{Z} q(Z) \ln p(Z|X, \theta) \\
& = \sum_{Z} q(Z) \ln \frac{p(X,Z|\theta)}{q(Z)} - \sum_{Z} q(Z) \ln \frac{p(Z|X,\theta)}{q(Z)} \\
& = L(q,\theta) + KL(q||p)
\end{align}
$q$は規格化されているので$\sum_{Z}q(Z)=1$です。従って上式は
\ln p(X|\theta) = L(q,\theta) + KL(q||p) \tag{1.4}
となります。ただし、$L$は関数$q$を入力としてある値を返す関数(=汎関数)で、$L(q,\theta)=\sum_{Z}q(Z)\ln \frac{p(X,Z|\theta)}{q(Z)}$で定義されます。またKL(q||p)はKLダイバージェンスなので常に0以上となり、$KL(q||p)$において$p=q$のとき0です。
(参考:KLダイバージェンス)
1.3 EMアルゴリズム
式(1.4)を$\theta$に関して最大化すればいいわけですが、これを実現するのがEMアルゴリズムです。
EMアルゴリズムはEステップとMステップと呼ばれる2つの操作を交互に繰り返し、式(1.4)を最大化します。
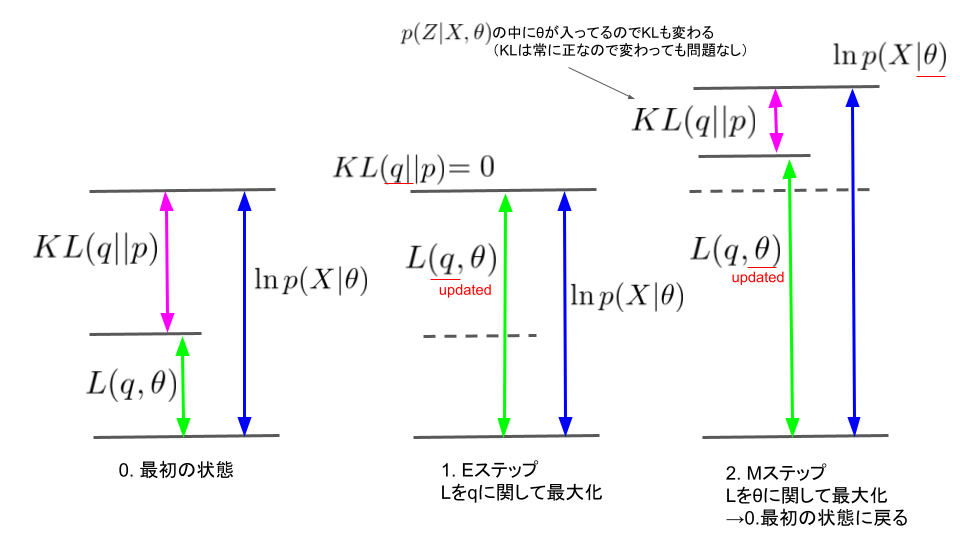
式(1.4)をみると、$KL(q||p)>0$のため$L(q,\theta)$は$\ln p(X|\theta)$の下界となります。そこで常に下界$L$を大きくし続ければ、いつか$\ln p(X|q, \theta)$の最大値にたどり着く、というのが基本的な考え方になります。図で表すと下のようになります。
1.3.1 Eステップ
Eステップでは$L(q,\theta)$を$q$に関して最大化します。$\theta$は固定されているため最大化するとはつまり$KL(q||p)=0$とするということです。すなわち、
q(Z) = p(Z|X,\theta) \tag{1.5}
として$q$を更新すればよいです。(同じ分布同士のKLダイバージェンスは0になるため。)
1.3.2 Mステップ
Mステップでは$L(q,\theta)$を$\theta$に関して最大化します。これはどういうことなのかを考えます。
今、式(1.5)で$q$が固定されていますが、この固定されている$\theta$を$\theta^{old}$とすると、$q$は、
q(Z) = p(Z|X,\theta^{old}) \tag{1.6}
ということになります。$L(q,\theta)=\sum_{Z}q(Z)\ln \frac{p(X,Z|\theta)}{q(Z)}$に上式を代入すると、
\begin{align}
L(q,\theta)&=\sum_{Z}p(Z|X,\theta^{old})\ln \frac{p(X,Z|\theta)}{p(Z|X,\theta^{old})} \\
&=\sum_{Z}p(Z|X,\theta^{old}) \ln p(X,Z|\theta)-\sum_{Z} p(Z|X,\theta^{old}) \ln p(Z|X,\theta^{old}) \\
&=Q(\theta,\theta^{old})+const. \tag{1.7}
\end{align}
今、$\theta$に関して最大化しようとしているので、$\theta$が現れない項は定数として$Q(\theta,\theta^{old})=\sum_{Z}p(Z|X,\theta^{old}) \ln p(X,Z|\theta)$のみを最大化すればよいとわかります。
1.1節の最後で$X$と潜在変数$Z$の同時分布が指数型分布族のような場合にEMアルゴリズムは使えると書きましたが、これは最大化したい$Q$の中で$p(X,Z|\theta)$が対数の中に入っているからです。もし$p(X,Z|\theta)$が対数の中に入れて$\theta$で微分するのが難しい場合、$Q$の最大化ができないためEMアルゴリズムを使うのは不適当です。
ここまで一般のEMアルゴリズムについて説明しました。ここからは具体的に混合ガウス分布の場合について考えていきます。
2. 混合ガウス分布のEMアルゴリズム
2.1 混合ガウス分布
今、$K$個のガウス分布で独立同分布から生成されるデータ点の分布を表現したいとして、$n$番目のデータ点$x_n$($0\leq n \leq N$)に対して混合ガウス分布によって$p(x_n)$を次のように定義します。
p(x_n)=\sum_{k=1}^{K}\pi_k \mathcal{N}(x_n|\mu_k, \Sigma_k)
ただし、$\pi_k$はガウス分布の混合係数で、$\sum_{k=1}^{K}\pi_k=1$です。また$\mathcal{N}(x_n|\mu_k, \Sigma_k)$で平均$\mu_k$, 共分散行列が$\Sigma_k$のガウス分布を表します。また$x_n, \mu_k$は$D$次元のベクトル、$\Sigma_k$は$D\times D$行列です。
したがって式(1.2)を利用して対数尤度は以下になります。
\ln p(X|\theta) = \sum_{n=1}^{N}\ln \bigg( \sum_{k=1}^{K}\pi_k \mathcal{N}(x_n|\mu_k, \Sigma_k)\bigg) \tag{2.1}
ここで潜在変数$Z$を導入します。あるデータ点$x_n$はK個のガウス分布のどれかに分類されるとして、分類されるのが$k$番目のガウス分布であるとき$z_{nk}=1$となるとします。そうでないとき$z_{nk}=0$です。$p(z_{nk}=1)=\pi_k$とすると、$Z$の同時分布は次になります。
p(Z)=\prod_{n=1}^{N}\prod_{k=1}^{K}\pi_k^{z_{nk}}
$z_{nk}=1$のときのみ$\pi_k$が積に加わり、$z_{nk}=0$では$1$がかけられるのみで分布には影響しません。
また、今は独立同分布を考えているため$z_{nk}=1$のときの$k$に対応するガウス分布のパラメータ$\mu_k, \Sigma_k$によって表現されるガウス分布を各点ごとにかけていくと$p(X|Z,\theta)$が求まります。すなわち、
\begin{align}
p(X|Z,\theta) &= \prod_{n=1}^{N}p(x_n|z_n) \\
&= \prod_{n=1}^{N}\prod_{k=1}^{K}\mathcal{N}(x_n|\mu_k, \Sigma_k)^{z_{nk}} \tag{2.2}
\end{align}
ただし、$\pi, \mu, \Sigma$などのパラメータをまとめて$\theta$と表現しました。
以上から、
\begin{align}
p(X,Z|\theta)&=p(Z|\theta)p(X|Z,\theta) \\
&=\prod_{n=1}^{N}\prod_{k=1}^{K}\pi_k^{z_{nk}}\mathcal{N}(x_n|\mu_k, \Sigma_k)^{z_{nk}} \tag{2.3}
\end{align}
となります。
さらに、
\begin{align}
p(Z|X,\theta) &= \frac{p(Z|X,\theta)p(X|\theta)}{p(X|\theta)}\\
&= \frac{p(X,Z|\theta)}{\sum_{Z}p(X,Z|\theta)}\\
&= \frac{\prod_{n=1}^{N}\prod_{k=1}^{K}(\pi_k \mathcal{N}(x_n|\mu_k, \Sigma_k))^{z_{nk}}}{\sum_{Z} \prod_{n=1}^{N}\prod_{j=1}^{K}(\pi_j\mathcal{N}(x_n|\mu_j,\Sigma_j))^{z_{nk}}} \\
\end{align}
分母に注目して、$z_{nk}=1$のときのみ$\pi_j\mathcal{N}(x_n|\mu_j,\Sigma_j)$の項が残るので、これを使うと、
\begin{align}
\sum_{Z} \prod_{n=1}^{N}\prod_{j=1}^{K}(\pi_j\mathcal{N}(x_n|\mu_j,\Sigma_j))^{z_{nk}}
&= \prod_{n=1}^{N}\sum_{j=1}^{K} \pi_j\mathcal{N}(x_n|\mu_j,\Sigma_j)
\end{align}
よって、$p(Z|X,\theta)$は次のようになります。
\begin{align}
p(Z|X,\theta) &= \frac{\prod_{n=1}^{N}\prod_{k=1}^{K}(\pi_k \mathcal{N}(x_n|\mu_k, \Sigma_k))^{z_{nk}}}{\sum_{Z}\prod_{n=1}^{N}\prod_{j=1}^{K}(\pi_j\mathcal{N}(x_n|\mu_j,\Sigma_j))^{z_{nk}}} \\
&= \frac{\prod_{n=1}^{N}\prod_{k=1}^{K}(\pi_k \mathcal{N}(x_n|\mu_k, \Sigma_k))^{z_{nk}}}{\prod_{n=1}^{N}\sum_{j=1}^{K} \pi_j\mathcal{N}(x_n|\mu_j,\Sigma_j)} \\
&=\prod_{n=1}^{N} \frac{\prod_{k=1}^{K}(\pi_k \mathcal{N}(x_n|\mu_k, \Sigma_k))^{z_{nk}}}{\sum_{j=1}^{K} \pi_j\mathcal{N}(x_n|\mu_j,\Sigma_j)} \tag{2.4}
\end{align}
ここでの計算は一旦ここまでにしておいて、Eステップ、Mステップでそれぞれどんな計算をすればいいか考えていきます。
2.2 Eステップ
Eステップでは式(1.5)に従って$Z$の条件付き分布を計算します。ここで、$z_{nk}=1$をみたすとして$n,k$を固定すると、式(2.4)から
\begin{align}
p(z_{nk}|x_n,\theta) &=\frac{\pi_k \mathcal{N}(x_n|\mu_k, \Sigma_k)}{\sum_{j=1}^{K} \pi_j\mathcal{N}(x_n|\mu_j,\Sigma_j)} \\
&=\gamma(z_{nk})
\end{align}
ただし、$\gamma(z_{nk})=p(z_{nk}|x_n, \theta)$として$\gamma$を定義しました。また、$p(z_k|X,\theta)=\prod_{n=1}^{N}p(z_{nk}|x_n,\theta)$を使っています。
2.3 Mステップ
Mステップは式(1.7)の$Q$を最大化します。
\begin{align}
Q(\theta,\theta^{old})&=\sum_{Z}p(Z|X,\theta^{old})\ln p(X,Z|\theta) \\
&=\sum_{n=1}^{N}\sum_{k=1}^{K}p(z_{nk}|x_n,\theta^{old})\ln p(x_n,z_{nk}|\theta) \\
&=\sum_{n=1}^{N}\sum_{k=1}^{K}\gamma(z_{nk})\ln \prod_{i=1}^{N} \prod_{j=1}^{K}(\pi_j \mathcal{N}(x_i|\mu_j,\Sigma_j))^{z_{ij}}\\
&=\sum_{n=1}^{N}\sum_{k=1}^{K}\gamma(z_{nk})\ln \pi_k \mathcal{N}(x_n|\mu_k,\Sigma_k)\\
&=\sum_{n=1}^{N}\sum_{k=1}^{K}\gamma(z_{nk})(\ln \pi_k + \ln \mathcal{N}(x_n|\mu_k,\Sigma_k)) \tag{2.5}
\end{align}
これを各パラメータについて最大化してやります。最大化するとは、極大値を見つけるのですから、
\frac{\partial}{\partial \theta}Q(\theta, \theta^{old})=0
をとけば良いです。
2.3.1 πの最適化
$\pi_k$については$\sum_{k=1}^{K}\pi_k=1$の制約があるため、これを満たすようにラグランジュの未定乗数法で解きます。
\frac{\partial}{\partial \pi_k}\big( Q(\theta, \theta^{old}) + \lambda (\sum_{k=1}^{K}\pi_k -1) \big) = 0 \\
\sum_{n=1}^{N}\gamma(z_{nk})\frac{1}{\pi_k}+\lambda = 0 \tag{2.6} \\
\sum_{n=1}^{N}\gamma(z_{nk})+\pi_k \lambda = 0 \\
\sum_{k=1}^{K}\sum_{n=1}^{N}\gamma(z_{nk})+\sum_{k=1}^{K} \pi_k \lambda = 0 \\
\lambda = -N
式(2.6)より、$\sum_{n=1}^{N}\gamma(z_{nk})=N_{k}$とすると、
\pi_k = \frac{N_k}{N} \tag{2.7}
2.3.2 μの最適化
$\mu_k$についても同様です。ただし$\mu_k$には制約条件はないのでそのまま解きます。
\mathcal{N(x_n|\mu_k,\Sigma_k)} = \frac{1}{(2\pi)^{D/2}}\frac{1}{|\Sigma_k|^{1/2}}\exp \bigg( -\frac{1}{2}(x_n-\mu_k)^T \Sigma_k^{-1}(x_n-\mu_k)\bigg)
なので、式(2.5)より、
\frac{\partial}{\partial \mu_k}Q(\theta, \theta^{old}) = 0 \\
\frac{\partial}{\partial \mu_k} \bigg( \sum_{n=1}^{N}\gamma(z_{nk})\big( -\frac{1}{2}(x_n-\mu_k)^T \Sigma_k^{-1}(x_n-\mu_k)\big) + const. \bigg) = 0 \\
\sum_{n=1}^{N}\gamma(z_{nk})\Sigma_k^{-1}(x_n-\mu_k) = 0 \\
両辺に$\Sigma_k$かけて、
\sum_{n=1}^{N}\gamma(z_{nk})x_n-N_k \mu_k=0 \\
\mu_k = \frac{1}{N_k}\sum_{n=1}^{N}\gamma(z_{nk})x_n \tag{2.8}
2.3.3 Σの最適化
$\Sigma_k$も最適化する。
\frac{\partial}{\partial \Sigma_k}Q(\theta, \theta^{old}) =0
$\Sigma_k$についてはやや計算が煩雑なので、導出は省略します。
単一のガウス分布の最尤解とほとんど同じです。(参考:ガウス分布の最尤解)
\Sigma_k = \frac{1}{N_k}\sum_{n=1}^{N}\gamma(z_{nk})(x_n-\mu_k)(x_n-\mu_k)^T \tag{2.9}
以上で必要な数式がすべて揃いました。
2.4 処理のまとめ
以上の数式をもとに実行すべき処理をまとめます。
2.4.0 初期値の設定
適当な$\pi_k, \mu_k, \Sigma_k$を設定します。
2.4.1 Eステップ
\gamma(z_{nk}) = \frac{\pi_k \mathcal{N}(x_n|\mu_k, \Sigma_k)}{\sum_{j=1}^{K} \pi_j\mathcal{N}(x_n|\mu_j,\Sigma_j)}
を計算します。
2.4.2 Mステップ
以下に従って各パラメータを更新する。
N_k = \sum_{n=1}^{N}\gamma(z_{nk}) \\
\pi_k = \frac{N_k}{N} \tag{2.7} \\
\mu_k = \frac{1}{N_k}\sum_{n=1}^{N}\gamma(z_{nk})x_n \tag{2.8}\\
\Sigma_k = \frac{1}{N_k}\sum_{n=1}^{N}\gamma(z_{nk})(x_n-\mu_k)(x_n-\mu_k)^T \tag{2.9}
2.4.1に戻って以降E及びMステップを繰り返す。
2.4.3 収束性の判定
以下の対数尤度が収束したらプログラムを終了する。
\ln p(X|\theta) = \sum_{n=1}^{N}\ln \bigg( \sum_{k=1}^{K}\pi_k \mathcal{N}(x_n|\mu_k, \Sigma_k)\bigg) \tag{2.1}
3. まとめ
以上で混合ガウス分布のEMアルゴリズムの説明は終了です。想定していたよりずっと分量が多くなってしまいました。もともとこの記事で実装まで記載しようと思っていたのですが、実装は次の記事に回しました。
もし致命的な誤りがありましたら指摘いただけますと幸いです。