はじめに
Pythonで機械学習を実装する際のデファクトスタンダードはscikit-learnだが、クラスタリングにおいては一部かゆいところに手が届いていない部分もあるため、pyclusteringが選択肢として入ってくる。
しかし、pyclusteringはscikit-learnと比較すると若干使いにくい部分があるため、利用方法の備忘のため、最も基本的なk-meansにおける実装例をまとめる。
K-meansの実行例
使用データ
from sklearn.datasets import make_blobs
X, _ = make_blobs(n_features=2, centers=5, random_state=1)
import matplotlib.pyplot as plt
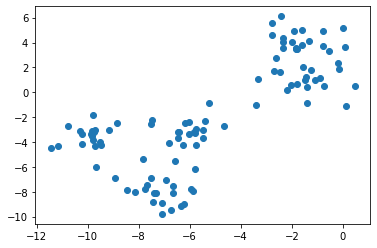
plt.scatter(X[:, 0], X[:, 1])
scikit-learn
scikit-learnを用いたk-meansの実装は以下の通りである。
なお、scikit-learnでの初期値設定方法はinitオプションで設定でき、デフォルトでha
k-means++になっている。
from sklearn.cluster import KMeans
sk_km = KMeans(n_clusters=3).fit(X)
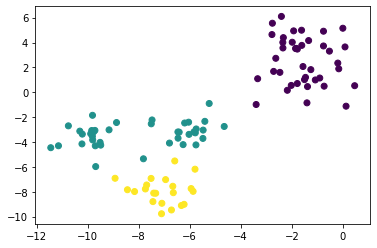
plt.scatter(X[:, 0], X[:, 1], c=sk_km.labels_)
pyclustering
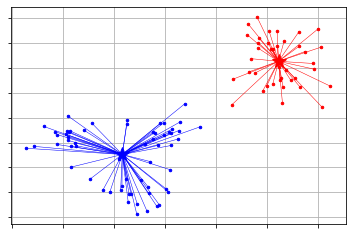
pyclusteringを用いたk-meansの実装は以下の通りである。
scikit-learnとは異なり、初期値設定とその後のクラスタ学習を分けて指定する必要がある。
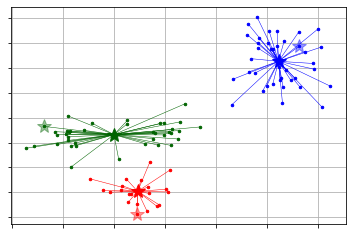
後、こちらで用意されている可視化用の関数を使うと少し情報がリッチになる。
from pyclustering.cluster import kmeans
from pyclustering.cluster.center_initializer import kmeans_plusplus_initializer
initial_centers = kmeans_plusplus_initializer(X, 3).initialize() # k-means++で初期値設定
pc_km = kmeans.kmeans(X, initial_centers) # kmeansクラスの定義
pc_km.process() # 学習の実行
_ = kmeans.kmeans_visualizer.show_clusters(X, pc_km.get_clusters(), pc_km.get_centers(), initial_centers=initial_centers) # 可視化
pyclusteringで得られたクラスタは、predictメソッドとget_clustersメソッドで参照できる。
predictでは、scikit-learnと同様に、入力データに対してラベルを返す。
get_clustersは、学習に使ったデータに対するインデックスをクラスタ別に返す。こちらはpandasなどで取り扱うのに適していないので、別途加工する必要がある。(predict使った方が簡単)
labels = pc_km.predict(X)
import numpy as np
clusters = pc_km.get_clusters()
labels = np.zeros((np.concatenate([np.array(x) for x in clusters]).size, ))
for i, label_index in enumerate(clusters):
labels[label_index] = i
クラスタ数の決定
scikit-learn
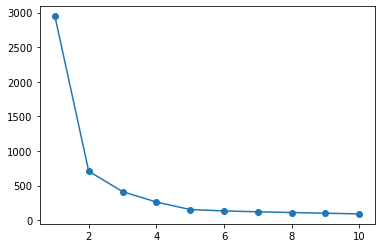
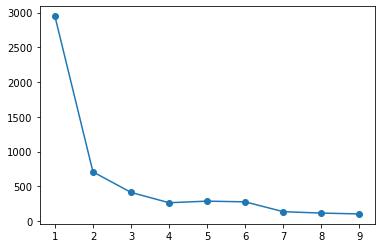
scikit-learnにおけるエルボー法について示す。
シルエット分析も可能だが、pyclusteringと同様に実装が複雑になるため、割愛する。
なお、どちらにおいても自動的にクラスタ数を決定することはできず、分析者が確認した上で決定する必要がある。
sse = list()
for i in range(1, 11):
km = KMeans(n_clusters=i).fit(X)
sse.append(km.inertia_)
plt.plot(range(1, 11), sse, 'o-')
pyclustering
pyclusteringの場合、エルボー法でクラスタ数の決定まで行ってくれる。
なお、クラスタ数は、探索範囲内でクラスタ内誤差平方和が大きく下がったクラスタ数を採用しているようだ。
from pyclustering.cluster.elbow import elbow
kmin, kmax = 1, 10 # 探索する値域
elb = elbow(X, kmin=kmin, kmax=kmax) # 探索範囲は、kmin~kmax-1までなことに注意
elb.process()
elb.get_amount() # クラスタ数を参照できる
plt.plot(range(kmin, kmax), elb.get_wce())
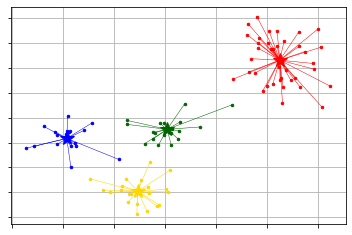
pyclusteringでは、x-meansやg-meansに対応しているため、それを利用することもできる。
from pyclustering.cluster import xmeans
from pyclustering.cluster.kmeans import kmeans_visualizer
initial_centers = xmeans.kmeans_plusplus_initializer(X, 2).initialize() # k=2以上で探索
xm = xmeans.xmeans(X, initial_centers=initial_centers, )
xm.process()
_ = kmeans_visualizer.show_clusters(X, xm.get_clusters(), xm.get_centers())
from pyclustering.cluster import gmeans
from pyclustering.cluster.kmeans import kmeans_visualizer
initial_centers = gmeans.kmeans_plusplus_initializer(X, 2).initialize()
gm = gmeans.gmeans(X, initial_centers=initial_centers, )
gm.process()
_ = kmeans_visualizer.show_clusters(X, gm.get_clusters(), gm.get_centers())
scikit-learnに比べ、pyclusteringが優位な点
敷居の低さで選ぶのであればscikit-learnではあるが、細かくクラスタリングアルゴリズムに調整したい場合はpyclusteringが優位である。
pyclusteringはそもそも対応しているアルゴリズムが多く、細かく処理内容を定義できる。例えば、距離定義をユークリッド距離からマンハッタン距離やユーザが定義した距離指標に変えることが出来る。
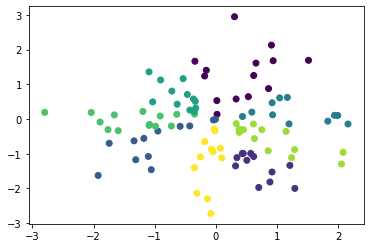
以下にコサイン距離でクラスタリンを行う例を示す。
※コサイン距離でやるだけなら、sphereclusterの方が簡単
import numpy as np
from pyclustering.cluster import kmeans
from pyclustering.cluster.center_initializer import kmeans_plusplus_initializer
from pyclustering.utils.metric import distance_metric, type_metric
X = np.random.normal(size=(100, 2))
def cosine_distance(x1, x2):
if len(x1.shape) == 1:
return 1 - np.dot(x1, x2) / (np.linalg.norm(x1) * np.linalg.norm(x2))
else:
return 1 - np.sum(np.multiply(x1, x2), axis=1) / (np.linalg.norm(x1, axis=1) * np.linalg.norm(x2, axis=1))
initial_centers = kmeans_plusplus_initializer(X, 8).initialize()
pc_km = kmeans.kmeans(X, initial_centers, metric=distance_metric(type_metric.USER_DEFINED, func=cosine_distance))
pc_km.process()
plt.scatter(X[:, 0], X[:, 1], c=pc_km.predict(X))