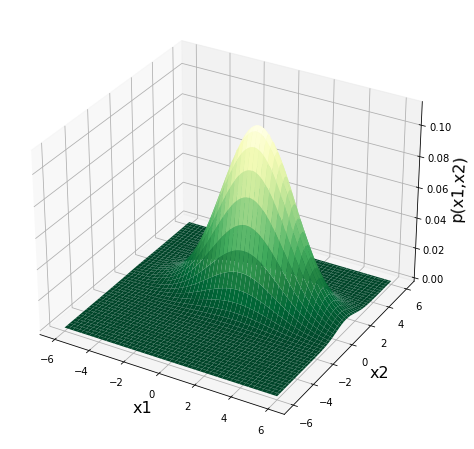
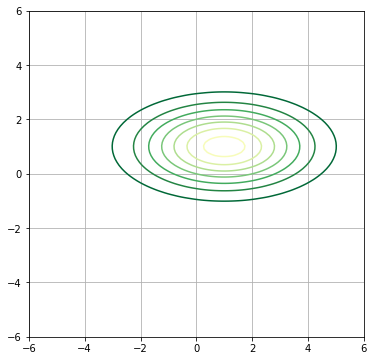
多次元正規分布の式、複雑すぎ問題
統計学の基本とも言える正規分布。
この正規分布は、下図のように多次元の変数でも定義することができます(多次元正規分布)
多次元正規分布は多くの機械学習アルゴリズム(主成分分析、ナイーブベイズ分類器、マハラノビスタグチ法、混合ガウスモデル等)で活用される確率分布であり、特に教師なし学習においては最重要理論の一つと言える存在であり、データ分析において避けては通れない理論と言えます。
一方で以下の多次元正規分布の式(確率密度関数)は多くの書籍で天下り的に与えられており、
N(\boldsymbol{x} \mid \boldsymbol{\mu}, \boldsymbol{\Sigma})=\frac{1}{(2\pi)^\frac{n}{2}}\frac{1}{|\boldsymbol{\Sigma}|^\frac{1}{2}} \exp \Bigl(-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^T \boldsymbol{\Sigma}^{-1} (\boldsymbol{x}-\boldsymbol{\mu}) \Bigr)
「複雑すぎて分からん!ちゃんと解説してくれ!」

とプンプンになってしまった方も多いかと思います。私もその一人です。
というわけで、精神の平静?を取り戻すべく上記の式の意味について調べたので、なるべく丁寧に解説したいと思います。
本文に進む前に
本記事の内容を理解するためには、「同時分布」「変数の独立性」「共分散」などに関する知識が必要です。
これらについては以下の記事で詳細に解説しましたので、まずはこちらをご一読頂ければと思います。
多次元正規分布の解説
多次元正規分布について、具体的な解説を進めていきます。
2次元の正規分布 → 3次元以上の正規分布
の順で進めます。
2次元正規分布
まずは理解しやすいよう2次元で解説します。
独立変数の2次元正規分布
2次元の正規分布をシンプルに考えると、以下のように1つ目の確率変数X1の正規分布と2つ目の確率変数X2の正規分布を掛け合わせた同時分布 $p(x_1,x_2)$が思い浮かびます。
p_1(x_1)=\frac{1}{\sqrt{2\pi\sigma_1^2}}\exp\Bigl(-\frac{1}{2\sigma_1^2}(x_1-\mu_1)^2\Bigr)\\
p_2(x_2)=\frac{1}{\sqrt{2\pi\sigma_2^2}}\exp\Bigl(-\frac{1}{2\sigma_2^2}(x_2-\mu_2)^2\Bigr)
p(x_1,x_2)=p_1(x_1)p_2(x_2)
上記の分布に関してPythonで等高線を作成し、可視化してみます($\mu_1=1, \mu_2=1, \sigma_1=1, \sigma_2=2$とする)
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# パラメータ
MU1 = 1
MU2 = 1
SIGMA1 = 2
SIGMA2 = 1
# (x1,x2)格子点を作成
x1_grid = np.linspace(-6, 6, 100)
x2_grid = np.linspace(-6, 6, 100)
X1, X2 = np.meshgrid(x1_grid, x2_grid)
# 同時分布関数
def p(x1, x2):
p1 = np.exp(-np.square(x1-MU1)/(2*SIGMA1**2))/np.sqrt(2*np.pi*SIGMA1)
p2 = np.exp(-np.square(x2-MU2)/(2*SIGMA2**2))/np.sqrt(2*np.pi*SIGMA2)
p = p1*p2
return p
# 同時分布をプロットするメソッド
def plot_joint_distribution(x1, x2):
# 同時分布を計算
P = p(X1, X2)
# 曲面をプロット
fig = plt.figure(figsize = (8, 8))
ax = fig.add_subplot(111, projection="3d")
ax.set_xlabel("x1", size = 16) # x1軸
ax.set_ylabel("x2", size = 16) # x2軸
ax.set_zlabel("p(x1,x2)", size = 16) # p軸
ax.plot_surface(X1, X2, P, cmap = "YlGn_r")
plt.show()
# 等高線をプロット
fig, axes = plt.subplots(1, 1, figsize=(6, 6))
plt.contour(X1, X2, P, cmap="YlGn_r")
ax.set_xlabel("x1", size = 16) # x1軸
ax.set_ylabel("x2", size = 16) # x2軸
plt.show()
# 同時分布プロット実行
plot_joint_distribution(X1, X2)
この分布は$p(x_1,x_2)=p_1(x_1)p_2(x_2)$という式から、変数X1とX2は独立であることが分かります。
よって上の等高線のように、この式ではどこで切っても断面形状が同じ分布しか再現できず、冒頭のような各変数が相関を持った斜めの分布が再現できません。
斜めの確率分布を再現するにはどうすれば良いでしょうか?
2次元正規分布と変数変換
斜めの確率分布を再現するには、行列による変数変換が有効です。
変換前の変数を(y1, y2)、変換後の変数を(x1, x2)とすると、変換行列
\boldsymbol{A}
=
\begin{pmatrix}
a & b \\
c & d
\end{pmatrix}
を用いて
\left(\begin{array}{c}
x_1 \\
x_2 \\
\end{array}\right)
=
\begin{pmatrix}
a & b \\
c & d
\end{pmatrix}
\left(\begin{array}{c}
y_1 \\
y_2 \\
\end{array}\right)
と表すことで、行列による変数変換が実現できます。
「行列」と聞いただけで頭が痛くなってきた方も多いかと思いますが、そんな時は変換要素を分解して、グラフで変換過程を可視化すると、理解が進むかと思います。
・QR分解と変換要素の分解
全てのnxn行列Aは、直交行列Qと上三角行列Rを使って以下のように分解できます。
\boldsymbol{A}=\boldsymbol{Q}\boldsymbol{R}

この分解をQR分解と呼び、Aが正則であればRの対角成分が全て正となって扱いやすくなります。
2x2行列においては任意のa,b,c,dに対して以下のように表せます(以後、Aが非正則な場合は片方の変数が消えて2次元正規分布が表現できないため、考慮しないこととします)
\begin{pmatrix}
a & b \\
c & d
\end{pmatrix}
=
\boldsymbol{Q}
\begin{pmatrix}
m_1 & m_3 \\
0 & m_2
\end{pmatrix}
・直交行列Qの分解
2x2行列では直交行列Qは
左右反転行列Mir→回転行列Rot
\boldsymbol{Q}=\boldsymbol{Rot}\cdot\boldsymbol{Mir}=
\begin{pmatrix}
\cos{\theta} & -\sin{\theta} \\
\sin{\theta} & \cos{\theta}
\end{pmatrix}
\begin{pmatrix}
1 & 0 \\
0 & (-1)^k
\end{pmatrix}
で表されます(参考1、参考2)
(kは0か1を取り、0ならば反転なし、1ならば反転ありを表します)
式を見ると分かりますが、反転がある場合
\boldsymbol{Q}=\begin{pmatrix}\cos{\theta} & \sin{\theta} \\ \sin{\theta} & -\cos{\theta} \end{pmatrix}
となり、反転がない場合
\boldsymbol{Q}=\begin{pmatrix}\cos{\theta} & -\sin{\theta} \\ \sin{\theta} & \cos{\theta} \end{pmatrix}
となるため、対角成分が一致しているかで反転の有無を見分ける事ができます (一致していなければ反転あり)
・上三角行列Rの分解
2x2行列では上三角行列Rは、以下のようにスキュー行列Skwと拡大行列Magで表されます。
(tanφの値域が-∞〜∞なので、m1tanφは任意のm3を表現できます)
\boldsymbol{R}=
\begin{pmatrix}
m_1 & m_3 \\
0 & m_2
\end{pmatrix}
=
\begin{pmatrix}
m_1 & m_1\tan\phi \\
0 & m_2
\end{pmatrix}
=
\begin{pmatrix}
m_1 & 0 \\
0 & m_2
\end{pmatrix}
\begin{pmatrix}
1 & \tan\phi \\
0 & 1
\end{pmatrix}
=\boldsymbol{Mag}\cdot\boldsymbol{Skw}
よって任意の2x2正則行列Aは、
\boldsymbol{A}=
\boldsymbol{Rot}\cdot\boldsymbol{Mir}\cdot\boldsymbol{Mag}\cdot\boldsymbol{Skw}
と「スキュー」→「拡大」→(「反転」)→「回転」の組み合わせで表せる事が分かります。
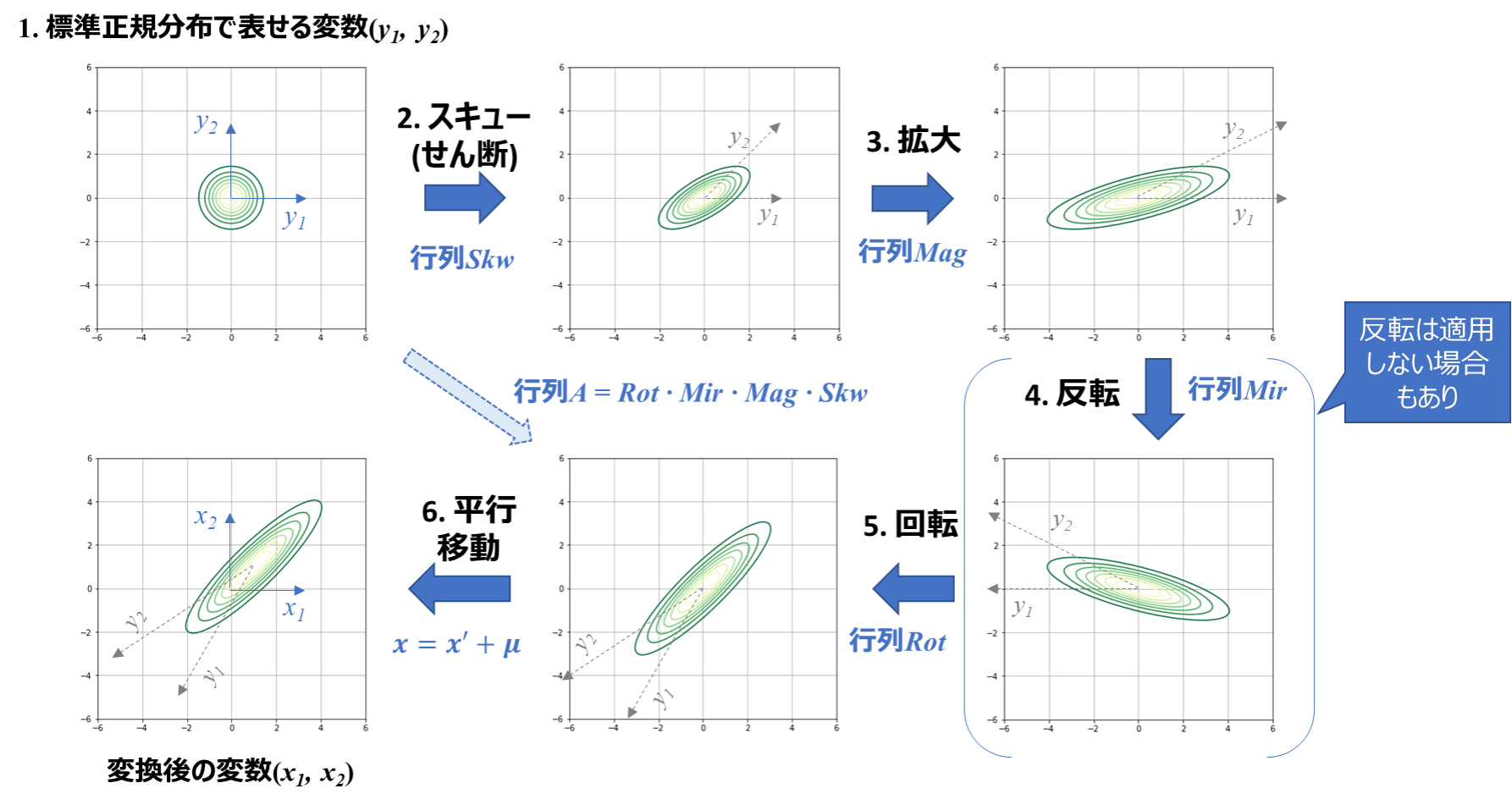
2次元正規分布における変数変換の可視化
2次元正規分布においては、下図のように独立2変数の標準正規分布(平均が全て0, 分散が全て1)をスタートとして
「1.標準正規分布」→「2.スキュー」→「3.拡大」→(「4.反転」)→「5.回転」
の順の変換を、前述のように2x2行列Aで表現できます。
上記変換に「6.平行移動」を加えた下図のような変換を実施することで、2次元の正規分布を定義することができます。
図を見れば明らかなように、行列Aによる変数変換で斜めの正規分布が再現できていますね!
各変換要素の解説
画像処理における座標変換(参考)をイメージすると分かりやすいですが、各変換要素の内容と行列について解説します。
1. 2変数の標準正規分布
2変数における標準正規分布は、先ほどの独立2変数の正規分布において、μ=0、σ=1を代入したものとなります。
この標準正規分布の関数を$q(y_1,y_2)$とすると、以下のように表せます。
q_1(y_1)=\frac{1}{\sqrt{2\pi}}\exp(-\frac{1}{2}y_1^2)\\
q_2(y_2)=\frac{1}{\sqrt{2\pi}}\exp(-\frac{1}{2}y_2^2)
q(y_1,y_2)=q_1(y_1)q_2(y_2)=\frac{1}{2\pi}\exp\bigl(-\frac{1}{2}(y_1^2+y_2^2)\bigr)
標準正規分布は各変数の周辺分布の掛け算で表されるため、確率変数y1, y2は独立であることが分かります。
また$y_1^2+y_2^2$の部分は、ベクトルy=(y1, y2)同士の内積、すなわち
\langle\boldsymbol{y},\boldsymbol{y}\rangle
となるため、2変数標準正規分布はベクトルで以下のようにも表記できます。
q(\boldsymbol{y})=\frac{1}{2\pi}\exp\bigl(-\frac{1}{2}\langle\boldsymbol{y},\boldsymbol{y}\rangle\bigr)
2. スキュー(せん断)
「スキュー」は馴染みのない言葉ですが、以下のように長方形を平行四辺形に変化させる変換を表します。
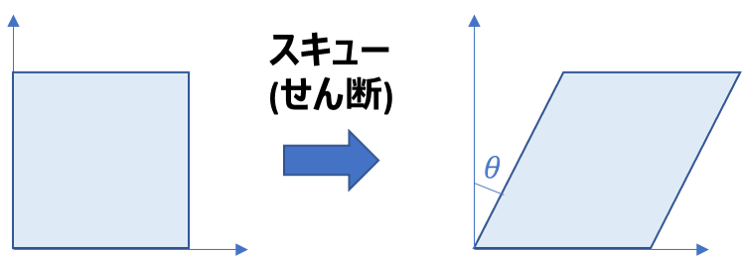
スキューを表す行列は、以下の式で表されます(φはスキュー角度)
\boldsymbol{Skw}=\begin{pmatrix}
1 & \tan{\phi} \\
0 & 1
\end{pmatrix}
3. 拡大
拡大・縮小を表す行列は、以下の式で表されます
\boldsymbol{Mag}=\begin{pmatrix}
m_1 & 0 \\
0 & m_2
\end{pmatrix}
$m_1, m_2$は、
m_1: y_1方向の拡大倍率\\
m_2: y_2方向の拡大倍率
を表しています。
4. 反転
反転を表す行列は、以下の式で表されます
(kは0か1を取り、0ならば反転なし、1ならば反転ありを表します)
\boldsymbol{Mir}=\begin{pmatrix}
1 & 0 \\
0 & (-1)^k
\end{pmatrix}
5. 回転
回転を表す行列は、以下の式で表されます(θは回転角度)
\boldsymbol{Rot}=\begin{pmatrix}
\cos{\theta} & -\sin{\theta} \\
\sin{\theta} & \cos{\theta}
\end{pmatrix}
6. 平行移動
平行移動は行列でも表現できますが、ベクトルで表現した方がシンプルです。
(前述のアフィン変換のように行列のサイズを1つ大きくして平行移動を行列で表現可能)
平行移動前の変数を(x1',x2')とすると、平行移動後の変数(x1, x2)は以下のように表されます。
\left(\begin{array}{c}
x_1 \\
x_2 \\
\end{array}\right)
=
\left(\begin{array}{c}
x_1' \\
x_2' \\
\end{array}\right)
+
\left(\begin{array}{c}
\mu_1 \\
\mu_2 \\
\end{array}\right)
以下のように、$\boldsymbol{\mu}=(\mu_{1}, \mu_{2})$は変換後の座標軸(x1, x2)における平均値を表しています
\mu_{1}: x_1方向の平均値\\
\mu_{2}: x_2方向の平均値
この式は以下のように一般化して表現可能です
\boldsymbol{x}=\boldsymbol{x'}+\boldsymbol{\mu}
・変数変換の一般式
前述の「2.スキュー」→「3.拡大」→(「4.反転」)→「5.回転」→「6.平行移動」の変換に対して、
変換前の確率変数\boldsymbol{y}=\left(\begin{array}{c}
y_1 \\
y_2 \\
\end{array}\right)
変換後の確率変数\boldsymbol{x}=\left(\begin{array}{c}
x_1 \\
x_2 \\
\end{array}\right)
の関係は、以下の式で表せます(反転がない場合は行列Mirは不要)
\boldsymbol{x}=(\boldsymbol{Rot}\cdot\boldsymbol{Mir}\cdot\boldsymbol{Mag}\cdot\boldsymbol{Skw})\boldsymbol{y}+\boldsymbol{\mu}\\
=\boldsymbol{A}\boldsymbol{y}+\boldsymbol{\mu}
Aの各成分を詳細に表記すると、以下のようになります。
\boldsymbol{A}=
\begin{pmatrix}
\cos{\theta} & -\sin{\theta} \\
\sin{\theta} & \cos{\theta}
\end{pmatrix}
\begin{pmatrix}
1 & 0 \\
0 & (-1)^k
\end{pmatrix}
\begin{pmatrix}
m_1 & 0 \\
0 & m_2
\end{pmatrix}
\begin{pmatrix}
1 & \tan{\phi} \\
0 & 1
\end{pmatrix}
=\begin{pmatrix}
m_1\cos{\theta} & m_1\cos{\theta}\tan{\phi}-(-1)^km_2\sin{\theta} \\
m_1\sin{\theta} & m_1\sin{\theta}\tan{\phi}+(-1)^km_2\cos{\theta}
\end{pmatrix}
以上で、行列Aによって座標がどのように変化するか可視化できたので、以降は簡単のため
a=m_1\cos{\theta} \\
b=m_1\cos{\theta}\tan{\phi}-(-1)^km_2\sin{\theta} \\
c=m_1\sin{\theta} \\
d=m_1\sin{\theta}\tan{\phi}+(-1)^km_2\cos{\theta}
とおき、
\boldsymbol{A}=
\begin{pmatrix}
a & b \\
c & d
\end{pmatrix}
と表すこととします。
【参考】特異値分解による変数変換の可視化
上ではQR分解により変数変換を可視化しましたが。別の行列分解法である特異値分解によっても可視化することができます (むしろQR変換よりも一般的かもしれません。参考)
特異値分解を用いると、行列A は以下のように分解する事ができます。
\boldsymbol{A} = \boldsymbol{U}\boldsymbol{\Gamma}^{\frac{1}{2}}\boldsymbol{V}^T\\
{\left\{\begin{array}{ll}
\boldsymbol{U}: \boldsymbol{A}\boldsymbol{A}^Tの固有ベクトルを列ベクトルとして並べた行列 (直交行列となる)\\
\boldsymbol{\Gamma}: \boldsymbol{A}\boldsymbol{A}^Tの固有値を並べた対角行列\\
\boldsymbol{V}: \boldsymbol{A}^T\boldsymbol{A}の固有ベクトルを列ベクトルとして並べた行列 (直交行列となる)
\end{array}\right.
}
特に今回のようにAが正方かつ正則な行列の場合、$\boldsymbol{\Gamma}^{\frac{1}{2}}$は$\boldsymbol{A}\boldsymbol{A}^T$の固有値の平方根を並べた対角行列となります
先ほどのQR分解と同様に、直交行列UおよびVは左右反転行列Mir→回転行列Rotに分解する事ができ (反転は適用されないこともある)、対角行列
\boldsymbol{\Gamma}^{\frac{1}{2}}=\begin{pmatrix} \Sigma_1 & 0 \\ 0 & \Sigma_2 \end{pmatrix}
は拡大行列Magとみなすことができます。
よってこれらを特異値分解の式$\boldsymbol{A} = \boldsymbol{U}\boldsymbol{\Gamma}^{\frac{1}{2}}\boldsymbol{V}^T$ に代入すると、
\boldsymbol{A}=
\boldsymbol{Rot}\cdot\boldsymbol{Mir}\cdot\boldsymbol{Mag}\cdot\boldsymbol{Mir}\cdot\boldsymbol{Rot}
と「回転」→(「反転」)→「拡大」→(「反転」)→「回転」の組み合わせで表せる事が分かります。
($\boldsymbol{V}$ は転置をとっているのでMirとRotを逆向きにしています)
さらに、最初の2つの「回転」→「反転」の操作では、円形の標準正規分布をスタートとすると形状が変化しないため、これらは無視する事ができます。

また「拡大」では円形の線対称は崩れないので、4個目の「反転」も無視できます。

よってこれらを
「回転」→(「反転」)→「拡大」→(「反転」)→「回転」
のように除いた
「拡大」→「回転」
の2操作のみで表せる事が分かります
(特異値分解後の行列Σが「拡大」を、Uが「回転」を表します)
上記変換に「平行移動」を加えた下図のような変換を実施することで、QR分解と同様に2次元の正規分布を定義することができます。

QR分解よりもシンプルな操作で表せる事が分かりました。
非独立変数の2次元正規分布
前節のように、変換前の標準正規分布で表せる座標系をy=(y1, y2)、変換後の座標系をx=(x1, x2)とすると、xは以下の式で表せます。
\boldsymbol{x}=\boldsymbol{A}\boldsymbol{y}+\boldsymbol{\mu}
この式を変形してyをxの式で表すと、
\boldsymbol{A}\boldsymbol{y}=\boldsymbol{x}-\boldsymbol{\mu}
\boldsymbol{y}=\boldsymbol{A}^{-1}(\boldsymbol{x}-\boldsymbol{\mu})
となります。
これを前述のyの標準正規分布のベクトル式に代入すると(<**y**,**y**>はy同士の内積を表します)
q(\boldsymbol{y})=\frac{1}{2\pi}\exp\bigl(-\frac{1}{2}\langle\boldsymbol{y},\boldsymbol{y}\rangle\bigr)\\
=\frac{1}{2\pi}\exp\bigl(-\frac{1}{2}\langle\boldsymbol{A}^{-1}(\boldsymbol{x}-\boldsymbol{\mu}),\boldsymbol{A}^{-1}(\boldsymbol{x}-\boldsymbol{\mu})\rangle\bigr)\\
転置と内積の関係$\langle\boldsymbol{A}\boldsymbol{v},\boldsymbol{w}\rangle=\langle\boldsymbol{v},\boldsymbol{A}^T\boldsymbol{w}\rangle$を適用して
=\frac{1}{2\pi}\exp\bigl(-\frac{1}{2}\langle(\boldsymbol{x}-\boldsymbol{\mu}),(\boldsymbol{A}^{-1})^T\boldsymbol{A}^{-1}(\boldsymbol{x}-\boldsymbol{\mu})\rangle\bigr)\\
転置と逆行列の関係$(\boldsymbol{A}^{-1})^T=(\boldsymbol{A}^T)^{-1}$を適用して
=\frac{1}{2\pi}\exp\bigl(-\frac{1}{2}\langle(\boldsymbol{x}-\boldsymbol{\mu}),(\boldsymbol{A}^T)^{-1}\boldsymbol{A}^{-1}(\boldsymbol{x}-\boldsymbol{\mu})\rangle\bigr)\\
逆行列同士の積の関係$\boldsymbol{A}^{-1}\boldsymbol{B}^{-1}=(\boldsymbol{B}\boldsymbol{A})^{-1}$を適用して
=\frac{1}{2\pi}\exp\bigl(-\frac{1}{2}\langle(\boldsymbol{x}-\boldsymbol{\mu}),(\boldsymbol{A}\boldsymbol{A}^T)^{-1}(\boldsymbol{x}-\boldsymbol{\mu})\rangle\bigr)\\
内積の表記法を$\langle\boldsymbol{v},\boldsymbol{w}\rangleから\boldsymbol{v}^T\boldsymbol{w}$(転置したベクトルとの積)に変更して
=\frac{1}{2\pi}\exp\bigl(-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^T(\boldsymbol{A}\boldsymbol{A}^T)^{-1}(\boldsymbol{x}-\boldsymbol{\mu})\bigr)\cdots④
・変数変換後の積分が1となるよう規格化
ここで、変数変換後も確率密度関数の「積分値=1」の条件を満たすよう規格化する必要があります。
すなわち、上記④=q(y1, y2)に対して、変数変換後の確率密度関数p(x1, x2)が
p(x_1, x_2)=Cq(y_1, y_2)
を満たすような規格化定数Cを求めます。
q(y1, y2)をp(x1, x2)に変数変換したとき、積分値はヤコビ行列(正方行列で変数変換する場合、その行列そのもの)を掛ける必要がある、すなわち$dx_1dx_2=\bigl|\boldsymbol{A}\bigr|dy_1dy_2$となります。
変数変換後の確率密度関数p(x1, x2)の全定義域での積分に、上記ヤコビ行列による変換を適用すると
\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}p(x_1,x_2)dx_1dx_2\\
=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}Cq(y_1,y_2)\bigl|\boldsymbol{A}\bigr|dy_1dy_2\\
=C\bigl|\boldsymbol{A}\bigr|\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}q(y_1,y_2)dy_1dy_2
ここで、q(y1, y2)の全定義域での積分$\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}q(y_1,y_2)dy_1dy_2=1$より
=C\bigl|\boldsymbol{A}\bigr|
確率密度関数p(x1, x2)の全定義域での積分は1となるので、上式=1となる必要があるため、
C\bigl|\boldsymbol{A}\bigr|=1\\
\therefore C=\frac{1}{\bigl|\boldsymbol{A}\bigr|}
これを④に適用して、
p(\boldsymbol{x})=p(x_1, x_2)=\frac{1}{\bigl|\boldsymbol{A}\bigr|}q(y_1, y_2)\\
=\frac{1}{2\pi}\frac{1}{\bigl|\boldsymbol{A}\bigr|}\exp\bigl(-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^T(\boldsymbol{A}\boldsymbol{A}^T)^{-1}(\boldsymbol{x}-\boldsymbol{\mu})\bigr)\cdots⑤
※上記では計算で規格化定数を求めましたが、こちらの記事のように、変数変換により行列式で表される平行四辺形分だけ面積が引き伸ばされるため、積分値(体積)=1を維持するためには引き伸ばした分高さを縮めるため、p(x)を行列式で割る必要がある、と理解すると直感的に分かりやすいかと思います。
・行列式の変換
天下り的ですが、$\boldsymbol{A}\boldsymbol{A}^T=\boldsymbol{\Sigma}$とおきます。
このとき、
\bigl|\boldsymbol{\Sigma}\bigr|=\bigl|\boldsymbol{A}\boldsymbol{A}^T\bigr|
積の行列式$\bigl|\boldsymbol{A}\boldsymbol{B}\bigr|=\bigl|\boldsymbol{A}\bigr|\bigl|\boldsymbol{B}\bigr|$より
=\bigl|\boldsymbol{A}\bigr|\bigl|\boldsymbol{A}^T\bigr|
転置行列の行列式$\bigl|\boldsymbol{A}^T\bigr|=\bigl|\boldsymbol{A}\bigr|$より
=\bigl|\boldsymbol{A}\bigr|\bigl|\boldsymbol{A}\bigr|\\
=\bigl|\boldsymbol{A}\bigr|^2\\
\therefore \bigl|\boldsymbol{A}\bigr|=\bigl|\boldsymbol{\Sigma}\bigr|^\frac{1}{2}
となります。これを⑤に代入して
p(\boldsymbol{x})=\frac{1}{2\pi}\frac{1}{|\boldsymbol{\Sigma}|^\frac{1}{2}}\exp\bigl(-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^T\boldsymbol{\Sigma}^{-1}(\boldsymbol{x}-\boldsymbol{\mu})\bigr)
これは冒頭の多次元正規分布の式のn=2の場合(nは変数の数)と等しくなることが分かります。
あとは天下り的に定義した$\boldsymbol{\Sigma}=\boldsymbol{A}\boldsymbol{A}^T$が分散共分散行列と等しくなることを証明すれば完了です。
なお、ここまでの式変形に使用した行列の公式は全て2次元に限らない正則行列に対して成立するため、
上式は3変数以上の正規分布についても成立します(nの値が変わる事にご注意下さい)
変数変換行列と分散共分散行列
前節で定義した$\boldsymbol{\Sigma}=\boldsymbol{A}\boldsymbol{A}^T$ですが、
これが分散共分散行列
\boldsymbol{\Sigma}=
\begin{pmatrix}
\sigma_1 & \sigma_{12} \\
\sigma_{12} & \sigma_2
\end{pmatrix}
{\left\{\begin{array}{ll}
\sigma_1 \cdots x_1の分散 \\
\sigma_2 \cdots x_2の分散 \\
\sigma_{12} \cdots x_1とx_2の共分散\\
\end{array}\right.
}
と等しいことを証明します
・前節の行列Σの各成分の値
まずはΣの具体的な値を求めてみます。
\boldsymbol{\Sigma}=\boldsymbol{A}\boldsymbol{A}^T\\
=
\begin{pmatrix}
a & b \\
c & d
\end{pmatrix}
\begin{pmatrix}
a & c \\
b & d
\end{pmatrix}\\
=
\begin{pmatrix}
a^2+b^2 & ac+bd \\
ac+bd & c^2+d^2
\end{pmatrix}
この各成分が、分散共分散行列の各成分と等しいことを示します。
・分散共分散行列の各成分の値
\left(\begin{array}{c}
x_1 \\
x_2 \\
\end{array}\right)
=
\begin{pmatrix}
a & b \\
c & d
\end{pmatrix}
\left(\begin{array}{c}
y_1 \\
y_2 \\
\end{array}\right)
から、
{\left\{\begin{array}{ll}
x_1=ay_1+by_2 \\
x_2=cy_1+dy_2 \\
\end{array}\right.
}
となることを踏まえ、変換後の変数x1,x2に対する分散、共分散を求めます。
x1の分散
まずx1の分散$\sigma_1$を求めると
\sigma_1=V[x_1]=V[ay_1+by_2]
和の分散の公式より
=V[ay_1]+V[by_2]+\rm{Cov}[ay_1,by_2]
=a^2V[y_1]+b^2V[y_2]+ab\rm{Cov}[y_1,y_2]
変数y1とy2は独立なので共分散は0となり
=a^2V[y_1]+b^2V[y_2]
変数y1とy2の確率分布q(y1,y2)は標準正規分布なので、分散は1となり
=a^2+b^2
よって$V[x_1]=a^2+b^2$となることが分かります
x2の分散
x2の分散$\sigma_1$は、x1のときと同様に
\sigma_2=V[x_2]=V[cy_1+dy_2]\\
=V[cy_1]+V[dy_2]+\rm{Cov}[cy_1,dy_2]\\
=c^2V[y_1]+d^2V[y_2]+cd\rm{Cov}[y_1,y_2]\\
=c^2V[y_1]+d^2V[y_2]\\
=c^2+d^2
よって$V[x_2]=c^2+d^2$となることが分かります
x1とx2の共分散
x2の分散$\sigma_1$は、x1のときと同様に
\sigma_{12}=\rm{Cov}[x_1,x_2]\\
=E\bigl[(x_1-E[x_1])(x_2-E[x_2]) \bigr]
=E[x_1x_2]-E[x_1]E[x_2]\\
=E[(ay_1+by_2)(cy_1+dy_2)]-E[ay_1+by_2]E[cy_1+dy_2]\\
=acE[y_1^2]+(ad+bc)E[y_1y_2]+bdE[y_2^2]-(aE[y_1]+bE[y_2])(cE[y_1]+dE[y_2])
ここで、確率分布q(y1,y2)は標準正規分布なので、y1およびy2の平均$E[y_1]=E[y_2]=0$となるので
=acE[y_1^2]+(ad+bc)E[y_1y_2]+bdE[y_2^2]
変数y1とy2は独立なので、$E[y_1y_2]=E[y_1]E[y_2]=0$が成り立つので
=acE[y_1^2]+bdE[y_2^2]
また、分散の公式$V[f(x)]=E[f(x)^2]-E[f(x)]^2より、E[y_1^2]=V[y_1]+E[y_1]^2=V[y_1]=1$から(y2についても同様)
=ac\cdot1+bd\cdot1\\
=ac+bd
よって
{\left\{\begin{array}{ll}
\sigma_1=a^2+b^2 \\
\sigma_2=c^2+d^2 \\
\sigma_{12}=ac+bd \\
\end{array}\right.
}
となり、前節の行列Σと各成分が等しい、すなわち前節の行列$\boldsymbol{\Sigma}=\boldsymbol{A}\boldsymbol{A}^T$は分散共分散行列であることが分かりました。
また、共分散の式$\sigma_{12}=ac+bd$を見ると分かりますが、共分散は負になることもあります(正負のイメージはこちら参照)
※ なお、前述の標準正規分布の分散共分散行列Σは、単位行列Iとなります。
3次元以上の場合
QR分解を始めとして、ここまで使用した行列の公式は全て2次元に限らない正則行列に対して成立するため、
分散共分散行列$\boldsymbol{\Sigma}=\boldsymbol{A}\boldsymbol{A}^T$は、3次元以上の正規分布に関しても成立します。
3次元以上においても直交行列は回転と反転を、上三角行列は拡大とスキューを表すので、行列Aはこれら(+平行移動)を組み合わせた変数変換行列となります。
このとき、分散共分散行列$\boldsymbol{\Sigma}$は各変数の分散Vおよび共分散Covを用いて
\boldsymbol{\Sigma}=
\left(
\begin{array}{ccc}
{\rm V}[x_1] & {\rm Cov}[x_1,x_2] & \ldots & {\rm Cov}[x_1,x_n]\\
{\rm Cov}[x_2,x_1] & {\rm V}[x_2] & \ldots & {\rm Cov}[x_2,x_n] \\
\vdots & \vdots & \ddots & \vdots \\
{\rm Cov}[x_n,x_1] & {\rm Cov}[x_n,x_2] & \ldots & {\rm V}[x_n]
\end{array}
\right)
のように求められます。
また行列$\boldsymbol{A}$は、n次元標準正規分布
q_1(y_1)=\frac{1}{\sqrt{2\pi}}\exp(-\frac{1}{2}y_1^2)\\
q_2(y_2)=\frac{1}{\sqrt{2\pi}}\exp(-\frac{1}{2}y_2^2)\\
:
q_n(y_n)=\frac{1}{\sqrt{2\pi}}\exp(-\frac{1}{2}y_n^2)
q(y_1,y_2 \cdots,y_n)=q_1(y_1)q_2(y_2)\cdots q_n(y_n)=\frac{1}{(2\pi)^{ \frac{n}{2}} }\exp\bigl(-\frac{1}{2}(y_1^2+y_2^2\cdots +y_n^2)\bigr)
で表せる独立な変数y=(y1,y2..,yn)を、実際に使用する変数x=(x1,x2..,xn)に変換するための変換行列です。
上記分散共分散行列Σおよび平均値ベクトルμを用いて、多次元正規分布$p(\boldsymbol{x} \mid \boldsymbol{\mu}, \boldsymbol{\Sigma})$は以下のように表されます(冒頭の式と同じ)
p(\boldsymbol{x} \mid \boldsymbol{\mu}, \boldsymbol{\Sigma})=\frac{1}{(2\pi)^\frac{n}{2}}\frac{1}{|\boldsymbol{\Sigma}|^\frac{1}{2}} \exp \Bigl(-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^T \boldsymbol{\Sigma}^{-1} (\boldsymbol{x}-\boldsymbol{\mu}) \Bigr)
まとめ
・多次元正規分布は正規分布を2次元以上の確率変数に拡張したもの
・多次元正規分布は、独立変数による標準正規分布を行列Aで変数変換することで表現できる
・変数変換行列Aは、スキュー、拡大、反転、回転、平行移動の組み合わせで表される
・分散共分散行列Σは、変数変換行列Aを使用して$\boldsymbol{\Sigma}=\boldsymbol{A}\boldsymbol{A}^T$と表せる
・多次元正規分布の確率密度関数は、分散共分散行列Σおよび平均ベクトルμから以下のように表せる
p(\boldsymbol{x})=\frac{1}{(2\pi)^\frac{n}{2}}\frac{1}{|\boldsymbol{\Sigma}|^\frac{1}{2}} \exp \Bigl(-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^T \boldsymbol{\Sigma}^{-1} (\boldsymbol{x}-\boldsymbol{\mu}) \Bigr)
出典
・統計学入門 東京大学出版会
・英語版Wikipedia(他次元正規分布)