はじめに
座標ベクトルに行列を掛けて別の座標に変換する事をアフィン変換と呼びます。通常アフィン変換は、次の5つの要素に分解できます。→具体例で学ぶ数学「アフィン変換の意味と4つの基本要素」, イメージングソリューション「アフィン変換」
- 平行移動
- 回転
- 拡大縮小
- 反転
- せん断
しかし、特異値分解で考えると、アフィン変換はせん断、反転を除く3つの基本要素に分解できると考えることもできます。
アフィン変換とは
n次元ベクトル$x$を$x'=Ax+b$に変換することをアフィン変換といいます。例として2次元の
A=
\begin{pmatrix}
1 & 2 \\
3 & -1
\end{pmatrix}
, b=
\begin{pmatrix}
2 \\
3
\end{pmatrix}
の場合を考えます。$x=(1,2)$の点が$x'=(7,4)$に変換されます。
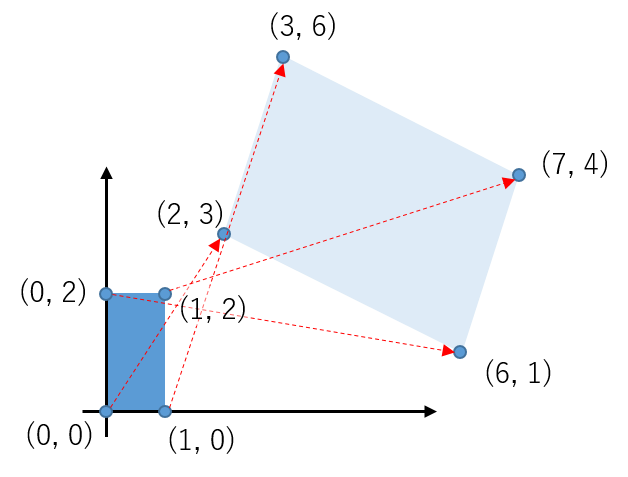
幅1高さ2の青い長方形が、右上の水色の傾いた平行四辺形に変換されます
アフィン変換を回転と拡大縮小とに分解する
この変換が、
回転10.9[deg] → X方向3.19倍、Y方向-2.19倍 → 回転79.1[deg]
(もう少し正確には
10.9 : 10.900704743175904
3.19 : 3.192582403567252
-2.19 : -2.192582403567252
79.1 : 79.09929525682409)
拡大縮小はX軸とY軸で別の拡大率を設定できるので、形が変わってしまいます。図では長方形が平行四辺形になっています。ちょっと変な気がするかもしれませんが、実際に計算して確認してみてください。
回転行列と拡大縮小行列の積を計算すると、以下のように元の行列に近い値なっていることを確認できます。
\begin{pmatrix}
\cos\theta_1 & -\sin\theta_1 \\
\sin\theta_1 & \cos\theta_1
\end{pmatrix}
\begin{pmatrix}
\alpha_1 & 0\\
0 & \alpha_2
\end{pmatrix}
\begin{pmatrix}
\cos\theta_2 & -\sin\theta_2 \\
\sin\theta_2 & \cos\theta_2
\end{pmatrix}
\approx
\begin{pmatrix}
1 & 2 \\
3 & -1
\end{pmatrix}
\\
\theta_1=10.900704743175904[deg] \\
\theta_2=79.09929525682409[deg] \\
\alpha_1=3.192582403567252 \\
\alpha_2=-2.192582403567252 \\
つまり、アフィン変換は回転とX軸Y軸方向の拡大縮小、そのあとの回転に分解できることがわかります。
このように分解できる理由について、以下に特異値分解を使って説明します
特異値分解
特異値分解は、「特異値分解を詳しく解説」にあるように、一般の行列を2つの直行行列で対角行列を挟んだ形に分解する手法です。
A=U\Gamma V^T
$U,V$は直交行列、直交行列は各列、各行が直交している行列なので、ほとんど回転行列なんだけど、座標軸の正の向きが逆になってる場合があるので、それを考えると、軸方向の反転$U_f$と回転行列$U_r$に分解できる。つまり
U=U_r U_f, V=V_r V_f
これを上の特異値分解の式に代入すると
A=U_r U_f\Gamma V_f^T V_r^T
=U_r (U_f\Gamma V_f^T) V_r^T
ゆえに、$X$を$A$でアフィン変換する$AX$の計算はベクトル$X$を$V_r^T$で回転し各軸方向に$\gamma_i$で拡大縮小、反転したあと$U_r$で再び回転する処理に分解されます。
まとめ
このように考えると、アフィン変換は
- 平行移動
- 回転
- 拡大縮小(反転含む)
と分解できると考えることができて、イメージしにくい「せん断」処理を考えなくていいので、便利なこともあるでしょう。というページでした。
