共分散とデータ分析
データ分析について勉強していると、共分散や分散共分散行列という言葉が良く出てきます。
一般的には以下のように変数同士の相関と関連したイメージを持たれている方が多いかと思います
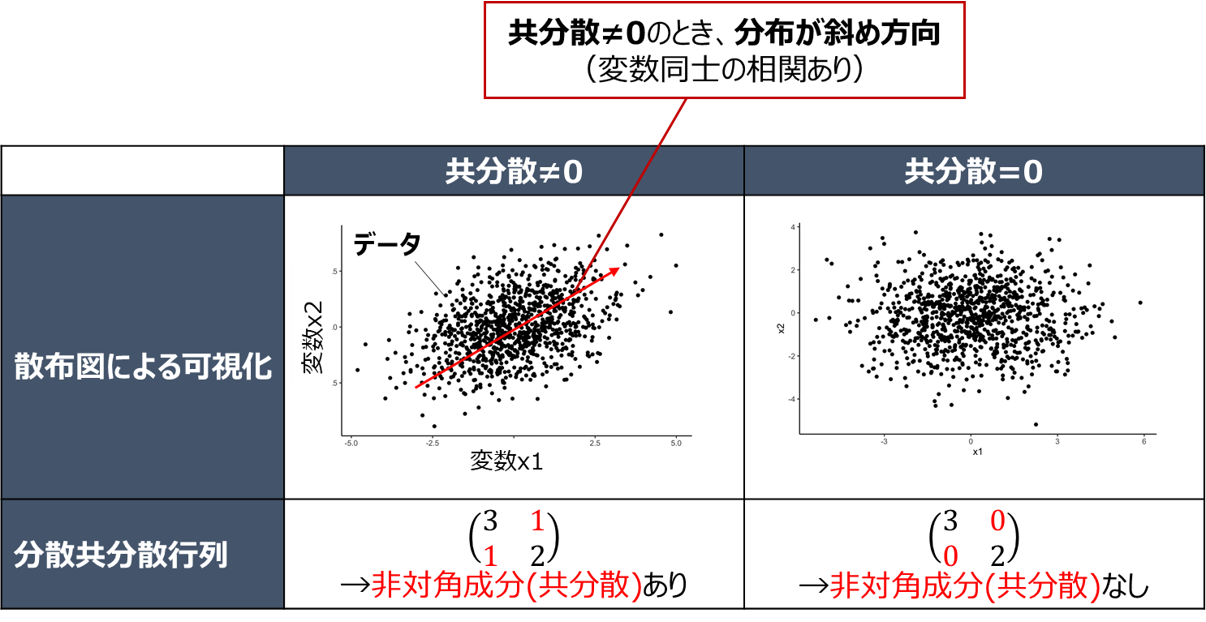
共分散は主成分分析や相関分析、ベイズ推定などの分野で必須とも言える知識ですが、
有名書籍ではさらっと流されている例も多く、
特に以下の多次元正規分布の分散共分散行列$\boldsymbol{\Sigma}$をいきなり与えられて、
N(\boldsymbol{x} \mid \boldsymbol{\mu}, \boldsymbol{\Sigma})=\frac{1}{(2\pi)^\frac{D}{2}}\frac{1}{|\boldsymbol{\Sigma}|^\frac{1}{2}} \exp \Bigl(-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^T \boldsymbol{\Sigma}^{-1} (\boldsymbol{x}-\boldsymbol{\mu}) \Bigr)
と面食らってしまった方も多いかと思います。
私も面食らったまま「分からなくても実装出来ればいいや」の精神で放置していました。
というわけで使用頻度の割にナゾの概念感が強い「共分散」ですが、故あってじっくり調べることとなったので、世の中の「わからん!」となっている方の疑問を少しでも解決できるよう、記事にまとめたいと思います。
※注意
私は数学の専門家ではないので、数学的な厳密性は保証できません(ルベーグ積分等の高度な内容にも触れません)。間違いがあればご指摘頂けるとありがたいです。
また、前述の経緯から途中式をなるべく省略しないことを心掛けて記事を書きました。
そのためかなり長いですが、その分式変形で詰まることなく理解が進むかと思うので、ぜひ最後まで一読頂ければと思います。
前提知識
共分散は2変数の確率分布において定義される値となります。
よって前提知識として以下が必要となるため、詳しく解説します。
・確率分布
・期待値
・分散
・多変数の確率分布と同時確率、周辺確率、条件付き確率
・多変数の期待値
・確率変数の独立
既にご存知の内容も多いかもしれませんが、いずれも統計学における重要な理論のため、復習も兼ねてご一読頂ければと思います。
確率分布
確率分布とは、JI Z 8101-1 : 1999によると
「確率変数がある値となる確率,又はある集合に属する確率を与える関数」
と定義されています。
上記の「関数」は、変数が連続か離散的かで以下のように呼び方が
変数が連続の場合: 確率密度関数
変数が離散的な場合: 確率質量関数
例えば、変数Xが下図のような確率密度関数p(x)に従う場合、変数xは3付近となる確率が最も高く、そこから離れる値ほど現れる確率が低くなります。
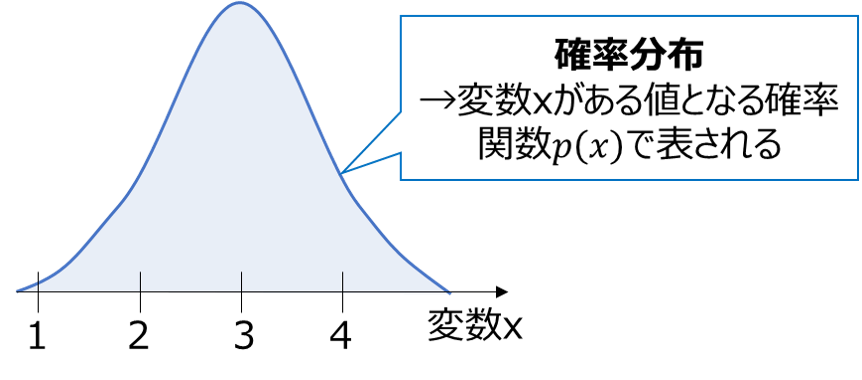
※厳密には確率密度関数p(x)は「変数がxとなる確率」ではなく、「変数が微小範囲x〜x+Δxの間に入る確率 ÷ Δx」であることにご注意ください。「存在確率そのもの」ではなく、存在確率の「密度」です。
また、上記の変数Xのように確率的に発生する変数を確率変数と呼びます。
確率変数は一般的にXのように大文字で表され、確率変数1つ1つの値をxのように小文字で表します。
p(x)のように関数の内部に入れる際は一般的に小文字が使用され、E(X)やV(X)のように平均や分散を表す際は大文字が使用されます。
(大雑把に理解することが目的であれば、小文字と大文字の違いはそこまで気にしなくとも良いです)
世の中の多くの現象はばらつきを持って確率的に変化するため、確率変数や確率分布はその表現に有用な理論と言えます。
1変数の確率分布
1変数において確率分布は、前述の変数Xのグラフのように単純な1変数関数で表すことができます。
例えば使用頻度の高い確率分布である正規分布は以下の式で表されます。
p(x)=\frac{1}{\sqrt{2\pi\sigma^2}}\exp\Bigl(-\frac{1}{2\sigma^2}(x-\mu)^2\Bigr)
ここで重要な事実として、原理上は確率分布に従う変数であっても、現実世界では有限のデータ(サンプル)しか観測できないため、確率分布の形状を知るためには限られたサンプルから推定する必要があります。
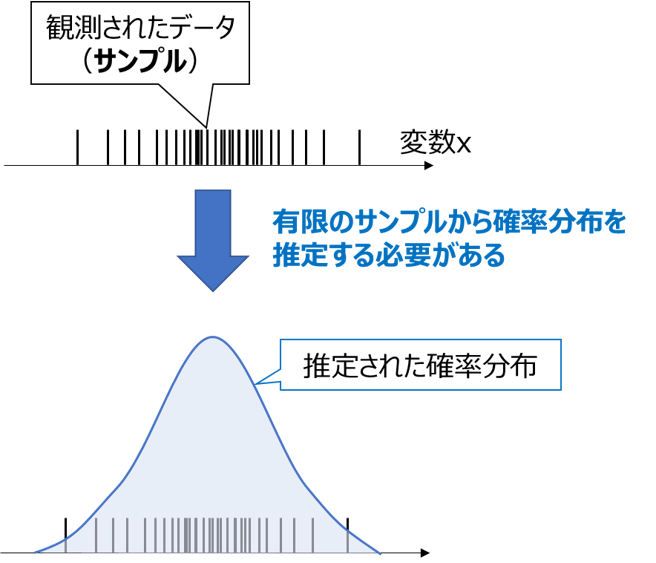
共分散も限られたサンプルから求めることができますが(後述)、求めた値は推定値であり、(頻度論における)真の値からは誤差が生じることにご注意ください。特にサンプルが少ないときは誤差が大きくなります
確率分布の全定義域での積分
確率分布は「確率を表現する」という特性上、全てのパターンの確率を足し合わせると1になる必要があります。
連続変数の確率分布では、下記のように全定義域(通常は-∞〜+∞)で積分すると1になることを表します。
\int_{-\infty}^{\infty} p(x)dx=1
確率変数が離散変数の場合、下記のように総和が1となります。
\sum_x p(x)=1
以降本記事では、確率変数が連続変数の場合を中心に議論を進めます。
期待値
期待値E[f(x)]とは、ある関数f(x)を確率分布p(x)で重み付けした平均となります。
期待値の定義式は書籍により微妙に異なりますが、
以下のPRMLでの定義式が今後の説明がしやすいので、こちらを採用します。
※本記事では連続確率分布を仮定して通常の積分(リーマン積分)で表記します
- 1変数における期待値の定義
E[f(x)]=\int_{-\infty}^{\infty} p(x)f(x)dx
特に以下の確率変数自身の期待値E[X](平均値)が、よく使用されます
- 確率変数の期待値(平均値)
E[X]=\int_{-\infty}^{\infty} xp(x)dx
上記は確率変数が連続変数の場合の期待値ですが、離散変数の場合以下のように積分が総和に変わります
- 1変数における期待値の定義(離散変数)
E[f(x)]=\sum_x p(x)f(x)
期待値の加法性
期待値には以下の加法性が成り立ちます
E[f(x)+g(x)]=E[f(x)]+E[g(x)]
これは以下の式で簡単に証明できます
E[f(x)+g(x)]=\int_{-\infty}^{\infty} p(x)(f(x)+g(x))dx\\
\int_{-\infty}^{\infty} \bigl(p(x)f(x)+p(x)g(x)\bigr)dx\\
\int_{-\infty}^{\infty} p(x)f(x)dx + \int_{-\infty}^{\infty} p(x)g(x)dx\\
=E[f(x)]+E[g(x)]
定数と期待値
定数cの期待値をとると、確率分布p(x)の積分が1となる性質から、定数cそのものが返されます
E[c]=\int_{-\infty}^{\infty} cp(x)dx\\
=c\int_{-\infty}^{\infty} p(x)dx\\
=c \cdot 1\\
=c
また、定数倍した関数の期待値E[cf(x)]は、元の期待値Eの定数倍cE[f(x)]となります
E[cf(x)]=\int_{-\infty}^{\infty} cf(x)p(x)dx\\
=c\int_{-\infty}^{\infty} f(x)p(x)dx\\
=cE[f(x)]
分散
分散V[f(x)]とは、ある関数f(x)が、期待値E[f(x)]の周りでどの程度ばらつくかを表す尺度で、以下の式で定義されます。
- 1変数における分散の定義(連続変数)
V[f(x)]=E \Bigl[\bigl(f(x)-E[f(x)]\bigr)^2 \Bigr]
この式は、以下のように式変形して簡略化すると計算しやすくなります
V[f(x)]=E \Bigl[\bigl(f(x)-E[f(x)]\bigr)^2 \Bigr]\\
=E \Bigl[f(x)^2-2E[f(x)]f(x)+E[f(x)]^2 \Bigr]\\
=E [f(x)^2]-2E\bigl[E[f(x)]f(x)\bigr]+E[f(x)]^2 \cdots期待値の加法性より \\
=E [f(x)^2]-2E[f(x)]E[f(x)]+E[f(x)]^2 \cdots 第二項のE[f(x)]は定数なので外出しできる \\
=E [f(x)^2]-2E[f(x)]^2+E[f(x)]^2 \\
=E [f(x)^2]-E[f(x)]^2
分散の直感的な理解
一般的によく使用されるのは、確率変数自身の分散
V[X]=E \Bigl[\bigl(X-E[X]\bigr)^2 \Bigr]
です。
この式の直感的な理解を考えてみます。
上記を文字に起こすと、
「平均からの二乗誤差$(X-E[X])^2$の期待値」
となるので、
「平均からのずれ」(偏差)の二乗平均をとったもの
と解釈すると、理解しやすいかと思います。
分散の積分表現
確率変数自身の分散は、期待値の定義に従って積分を用いると以下のように表されます。
V[X]=E \Bigl[\bigl(X-E[X]\bigr)^2 \Bigr]\\
=\int_{-\infty}^{\infty} \bigl(x-E[X]\bigr)^2p(x)dx
※平均値E[X]は積分内では定数として扱えます
定数倍の分散
定数倍した関数の分散V[cf(x)]は、元の分散の定数の2乗倍$c^2V[f(x)]$となります
V[cf(x)]=E \Bigl[\bigl(cf(x)-E[cf(x)]\bigr)^2 \Bigr]\\
=E \Bigl[\bigl(cf(x)-cE[f(x)]\bigr)^2 \Bigr]\\
=E \Bigl[c^2\bigl(f(x)-E[f(x)]\bigr)^2 \Bigr]\\
=c^2E \Bigl[\bigl(f(x)-E[f(x)]\bigr)^2 \Bigr]\\
=c^2V[f(x)]
多変数の確率分布
確率変数が多変数の時、確率分布は多変数関数で表されます。
例えば確率変数X1,X2の2次元で構成される正規分布の関数は、以下のような山型の3Dグラフで表す事ができます。
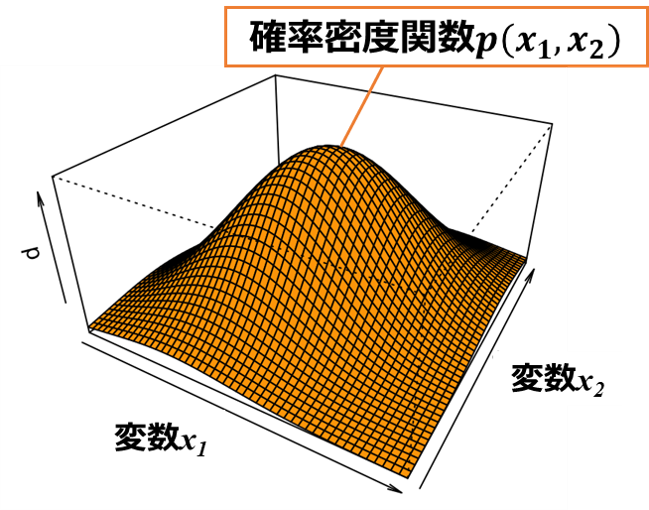
上記3Dグラフは、
「変数X1(横軸)と変数X2(縦軸)が同時にある値をとる確率が、関数p(x1,x2)の値(グラフの高さ)となる」
と解釈できます。
このような複数の変数が同時にある値をとる確率を同時確率と呼び、多変数の確率分布は基本的にこの同時確率で表されます。
多変数においては、n個の確率変数(X1, X2... , Xn)の値をベクトルxで表し、以下のようにxの関数で確率分布p(x)を表します。
p(x_1, x_2,\cdots,x_n)=p(\boldsymbol{x})
例えば多変数の正規分布(冒頭で紹介したもの)は、以下の関数で表されます
p(\boldsymbol{x})=\frac{1}{(2\pi)^\frac{D}{2}}\frac{1}{|\boldsymbol{\Sigma}|^\frac{1}{2}} \exp \Bigl(-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^T \boldsymbol{\Sigma}^{-1} (\boldsymbol{x}-\boldsymbol{\mu}) \Bigr)
Σとμというパラメータが現れますが、詳細はこちらの記事で紹介します。
多変数確率分布でも1変数と同様、積分すると1になる必要があります。
※積分範囲は全変数の定義域
\int_{-\infty}^{\infty} p(\boldsymbol{x})d\boldsymbol{x}=1
例えば2つの確率変数x1とx2からなる場合、以下の式が成り立つ必要があります。
\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} p(x_1, x_2)dx_1 dx_2 =1
周辺確率
ある変数を積分することで消去し、より少ない変数で表せるようにした確率分布を周辺確率と呼びます。
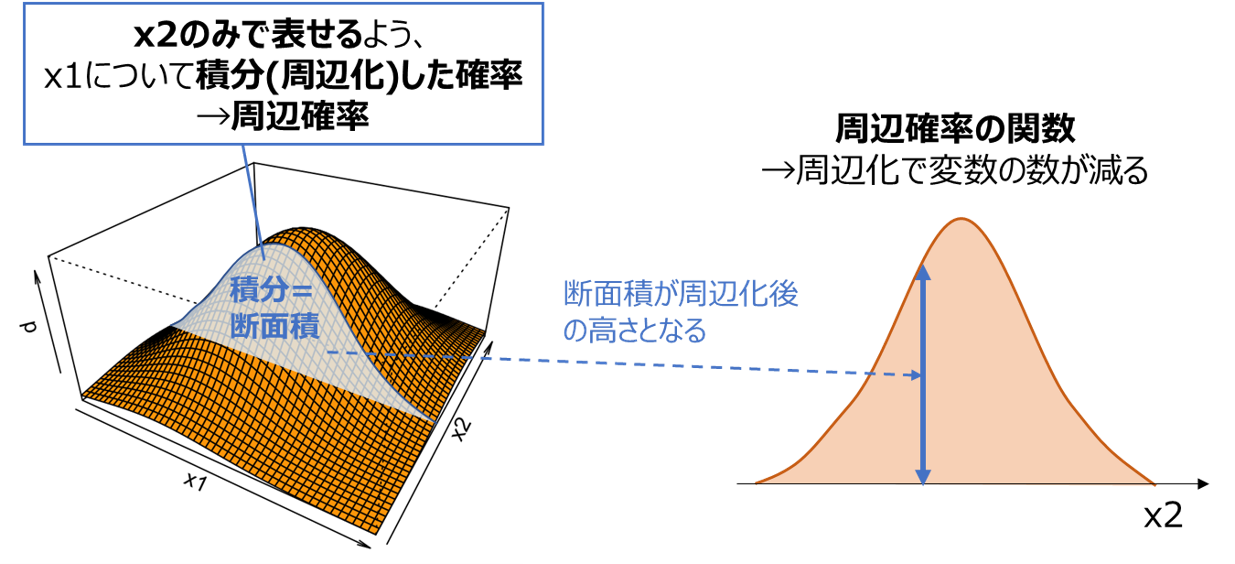
上の例では、x1について周辺化してx2のみで表せるようにした確率分布$p(x_2)$を求めており、以下の式で表せます。
p(x_2)=\int_{-\infty}^{\infty} p(x_1, x_2)dx_1
上記の関数ではx1が消去され、x2のみで表せる(変数が減る)ことが分かります。
・確率の加法定理
上記のように周辺確率が同時確率の積分で表せることを、確率の加法定理とも呼びます。
・周辺確率の積分
周辺確率も「確率の和=1」の原則に則り、残った変数の定義域で積分すると1となります
\int_{-\infty}^{\infty} p(x_2)dx_2=1
条件付き確率
ある変数を固定、あるいは変数同士に条件を加えることで、より少ない変数で表せるようにした確率分布を条件付き確率と呼びます。
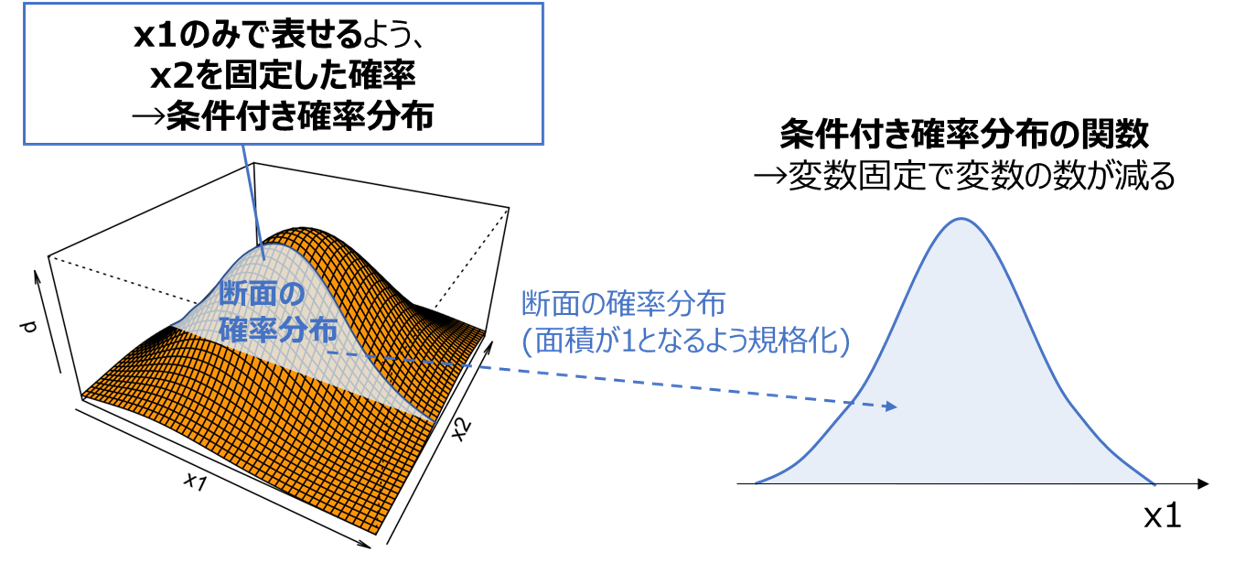
上の例では、x2を固定してx1のみで表せるようにした確率分布$p(x_1 \mid x_2)$を求めており、以下の式で表されます。
p(x_1 \mid x_2)=\frac{p(x_1, x_2)}{p(x_2)}
例えば、$x_2=a$という条件を加えた場合、以下のように定式化できます。
p(x_1 \mid x_2=a)=\frac{p(x_1, a)}{p(x_2=a)}
※分母の$p(x_2=a)$は、x1で周辺化した周辺確率(上の図の断面積)のx2=aにおける値を表しており、条件付き確率の積分が1となる(確率分布の条件を満たす)ための規格化定数として使用されています。
また上記の関数ではx2が消去され、x1のみで表せる(変数が減る)ことが分かります。
上の例では変数の値を定数で固定していますが、例えば
$x_1^2+x_2^2=1$
のように変数同士に制約条件を加え、この制約条件で変数変換して片方の変数を消去することも可能です。
条件付き確率は「変数を減らす」という意味では周辺確率と似ていますが、以下の違いがあることにご注意ください
| 名称 | 変数を消去する方法 | 消去される変数 |
|---|---|---|
| 周辺確率 | 積分 | 積分に使用した変数 |
| 条件付き確率 | 変数を固定、または変数同士に制約条件を追加 | 固定した変数 |
・条件付き確率の積分
条件付き確率も「確率の和=1」の原則に則り、残った変数の定義域で積分すると1となります
\int_{-\infty}^{\infty} p(x_1 \mid x_2)dx_1=1
証明は以下のようになります
\int_{-\infty}^{\infty} p(x_1 \mid x_2)dx_1=\int_{-\infty}^{\infty} \frac{p(x_1, x_2)}{p(x_2)}dx_1
$p(x_2)はx_1$に依存せず積分の外に出せるので
=\frac{1}{p(x_2)}\int_{-\infty}^{\infty}p(x_1, x_2)dx_1\\
=\frac{p(x_2)}{p(x_2)}\\
=1
上式を見ると、分母の$p(x_2)$が積分=1となるための規格化定数の役割を果たすことが分かるかと思います。
確率の乗法定理
p(x_1 \mid x_2)=\frac{p(x_1, x_2)}{p(x_2)}
を変形すると、同時確率は条件付き確率と周辺確率の積となることが分かります。
p(x_1, x_2)=p(x_1 \mid x_2)p(x_2)
 この関係を**確率の乗法定理**と呼びます
この関係を**確率の乗法定理**と呼びます
多変数確率分布の期待値
多変数確率分布の期待値は、どの変数について期待値をとるのか(積分に使用する変数)に注意する必要があります。
具体的には、「期待値」と「条件付き期待値」の違いを把握する事が重要です。
(周辺化した関数の期待値を求めることもできますが、ここでは割愛します)
後述の共分散の解説では基本的に「期待値」の方を使用しますが、本項では違いを明確化するため両者を解説します。
期待値
単に「期待値」と呼ぶと、全変数に対して求めた期待値を表すことが多いです。
期待値E[f(x)]は、全ての確率変数の定義域に対して、関数f(x)とp(x)の積を積分した値となります。
E[f(\boldsymbol{x})]=\int_{-\infty}^{\infty} p(\boldsymbol{x})f(\boldsymbol{x})d\boldsymbol{x}
特に各確率変数の期待値$E[X_n]$(平均値)が、よく使用されます
E[X_n]=\int_{-\infty}^{\infty} x_np(\boldsymbol{x})d\boldsymbol{x}
例えば2つの確率変数X1とX2からなる確率分布p(x1,x2)に対し、関数f(x1,x2)の期待値E[f(x1,x2)]を求めたい場合、以下の積分値を求めます。
E[f(x_1, x_2)]=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} p(x_1, x_2)f(x_1, x_2)dx_1 dx_2
このケースで各確率変数の期待値E[X1]およびE[X2](平均値)は、以下のように求められます。
E[X_1]=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} x_1p(x_1, x_2)dx_1 dx_2\\
E[X_2]=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} x_2p(x_1, x_2)dx_1 dx_2
期待値E[X1]およびE[X2]は、下図のように確率分布(同時確率)$p(x_1,x_2)$の重心のx1座標、x2座標とみなすと理解しやすいかと思います。
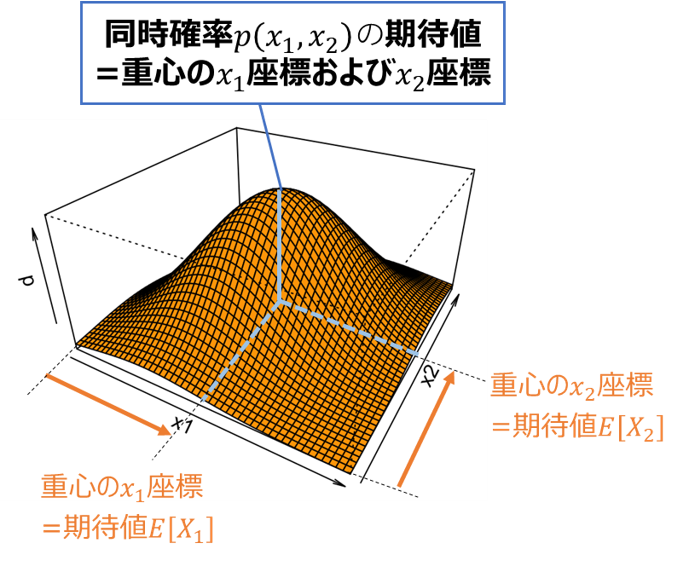
・複数変数の期待値の加法性
先ほど複数の関数における期待値の加法性を解説しましたが、複数の確率変数についても加法性は成立します
E[X_1+X_2]=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} p(x_1, x_2)(x_1+x_2)dx_1 dx_2\\
=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} x_1p(x_1, x_2)dx_1 dx_2 + \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} x_2p(x_1, x_2)dx_1 dx_2\\
=E[X_1]+E[X_2]
条件付き期待値
条件付き期待値とは、ある変数を固定、あるいは条件を加えた際の条件付き確率$p(x_1 \mid x_2)$を求め、
その条件付き確率と関数f(x)から求めた期待値を指します。

例えば上図のように、x2に条件を加えた際の、関数f(x1)に対する条件付き期待値$E[f(x_1) \mid x_2]$を求めたい場合、以下の積分値を求めます。
E[f(x_1) \mid x_2]=\int_{-\infty}^{\infty} p(x_1 \mid x_2)f(x_1)dx_1
上記の関数では期待値をとったx1が消去され、x2のみで表せる(変数が減る)ことが分かります。
特に以下の確率変数自身の条件付き期待値$E[x_1 \mid x_2]$が、よく使用されます
E[x_1 \mid x_2]=\int_{-\infty}^{\infty} p(x_1 \mid x_2)x_1dx_1
条件付き期待値は期待値をとった変数が消去され、最初に条件として固定した変数が残ります。
以下のように条件付き確率とは消去される変数が逆となることにご注意ください
| 名称 | 変数を消去する方法 | 消去される変数 |
|---|---|---|
| 条件付き確率 | 変数を固定、または変数同士に制約条件を追加 | 固定した変数 |
| 条件付き期待値 | 固定した変数以外に対して期待値をとる | 固定した変数以外 |
確率変数の独立
JIS Z 8101-1では、
「確率変数XとYが独立である」
とは、同時確率F(x,y)とxの周辺確率G(x)、yの周辺確率H (y)に以下の関係が成り立つこと
F (x, y)=G (x) ・H (y)
と定義されています。
これを今までの本記事での表記(≒PRMLでの表記)に統一すると、以下のように書き直せます。
・「変数X1とX2が独立であること」の必要十分条件
p(x_1,x_2)=p(x_1)p(x_2)
{\left\{\begin{array}{ll}
p(x_1,x_2):X_1とX_2の同時確率\\
p(x_1):X_1の周辺確率\\
p(x_2):X_2の周辺確率\\
\end{array}\right.
}
「独立」の感覚的な理解
「確率変数X1とX2が独立である」とは、どのような状態を指すのでしょうか?
感覚的には、「X2がどのような値でも、X1の値に影響を与えない」(逆も然り)
と解釈できそうですが、
確率分布では「X2がどのような値でも、X1の確率分布形状が変わらない」とみなすと分かりやすいかと思います。
ここで「X2がある値の時のX1の確率分布」は、前述した条件付き確率$p(x_1 \mid x_2)$そのものです。
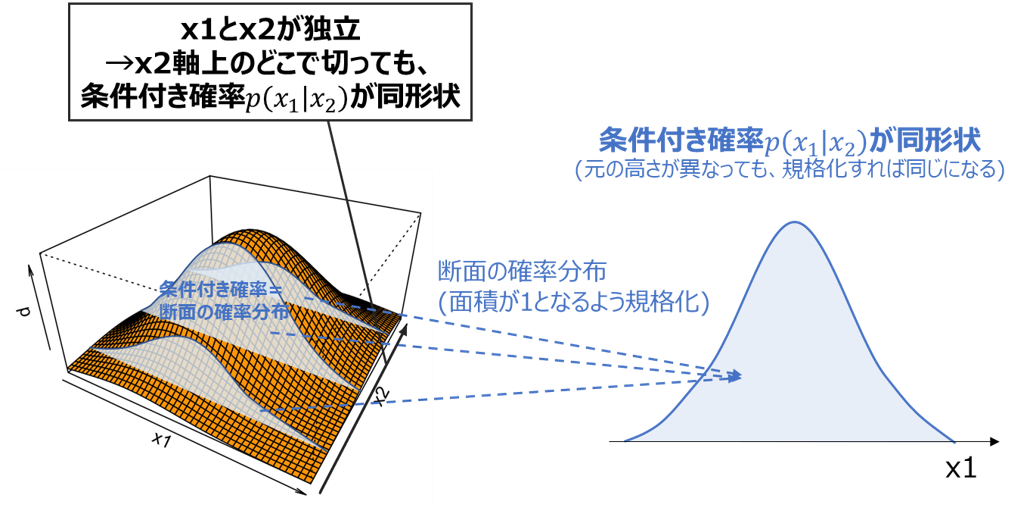
これがX2の値によらない、すなわちX1のみの関数で表されることは、以下のように立式できます。
・「変数X1とX2が独立であること」の感覚的な理解
条件付き確率p(x_1 \mid x_2)がx_1のみの関数で表される\\
かつ\\
条件付き確率p(x_2 \mid x_1)がx_2のみの関数で表される
これが、先ほどのJISの定義と必要十分条件になっていることを確認しましょう。
- 証明
上式の「x1のみの関数」をg(x1)、「x2のみの関数」をh(x2)とすると、以下のように書き直せます。
p(x_1 \mid x_2)=g(x_1)\\
かつ\\
p(x_2 \mid x_1)=h(x_2)
確率の乗法定理を適用すると
\frac{p(x_1,x_2)}{p(x_2)}=g(x_1)\\
かつ\\
\frac{p(x_2,x_1)}{p(x_1)}=h(x_2)
式を変形して
p(x_1,x_2)=g(x_1)p(x_2) \cdots ①\\
かつ\\
p(x_2,x_1)=h(x_2)p(x_1) \cdots ②
式①に着目して両辺をx2で積分すると
\int_{-\infty}^{\infty}p(x_1,x_2)dx_2 = \int_{-\infty}^{\infty}p(x_2)g(x_1)dx_2
左辺は周辺確率p(x1)の定義そのもので、右辺のg(x1)はx2によらないため積分の外に出せるため、以下のように式変形できます
p(x_1) = g(x_1)\int_{-\infty}^{\infty}p(x_2)dx_2
右辺の積分は周辺確率のx2による積分のため、1となることから
p(x_1) = g(x_1)
上式を式①に代入して
p(x_1,x_2)=g(x_1)p(x_2)\\
=p(x_1)p(x_2)
JISの定義が導き出せました。
注意点として、積分を適用した時点で十分条件となってしまうので、必要条件(JISの定義からスタートして「感覚的な理解」を示す)も証明する必要があります。
確率の乗法定理にJISの定義式を代入して
p(x_1 \mid x_2)=\frac{p(x_1,x_2)}{p(x_2)}\\
=\frac{p(x_1)p(x_2)}{p(x_2)}\\
=p(x_1) \cdots x_1のみの式で表せる
$p(x_2 \mid x_1)=p(x_2)$も同様に成り立ち、x2のみの式で表せるので、
条件付き確率p(x_1 \mid x_2)がx_1のみの関数で表される\\
かつ\\
条件付き確率p(x_2 \mid x_1)がx_2のみの関数で表される
が成り立つことが示せました。
独立と条件付き確率
上で示したように、変数x1とx2が独立であれば、条件付き確率は周辺確率と等しくなります。
p(x_2 \mid x_1)=p(x_2)\\
p(x_1 \mid x_2)=p(x_1)
独立と積の期待値
変数x1とx2が独立の場合に成り立つ重要な性質として、「積の期待値」が「期待値の積」となることです。
・独立変数の積の期待値
E[X_1 X_2]=E[X_1]E[X_2]
- 証明
積$X_1X_2$の期待値は、以下のように表されます。
E[X_1X_2]=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} x_1x_2 p(x_1, x_2)dx_1 dx_2\\
前述のようにx1とx2が独立の場合、$p(x_1,x_2)=p(x_1)p(x_2)$が成り立つので、代入して
=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} x_1x_2 p(x_1)p(x_2)dx_1 dx_2\\
x2およびp(x2)はx1に依存しない(x2のみで表される)ので、定数とみなしてx1に対する積分の外側に出せます。
=\int_{-\infty}^{\infty} x_2p(x_2) \Bigl(\int_{-\infty}^{\infty} x_1 p(x_1)dx_1 \Bigr) dx_2 \cdots③
ここで内側の積分を考えます。積分の中に$1=\int_{-\infty}^{\infty} p(x_2)dx_2$を代入して
\int_{-\infty}^{\infty} x_1 p(x_1)dx_1=\int_{-\infty}^{\infty} \Bigl(\int_{-\infty}^{\infty} p(x_2)dx_2\Bigr) x_1p(x_1)dx_1
x1およびp(x1)はx2に依存しないので、内側の積分の中に入れて
=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} x_1 p(x_1)p(x_2)dx_1dx_2\\
=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} x_1 p(x_1,x_2)dx_1dx_2\\
=E[X_1]
これを③に代入すると
E[X_1 X_2]=\int_{-\infty}^{\infty} x_2p(x_2)E[X_1]dx_2
$E[X_1]$は定数なので積分の外に出すと
E[X_1 X_2]=E[X_1]\int_{-\infty}^{\infty} x_2p(x_2)dx_2
先ほどと同様に$\int_{-\infty}^{\infty} x_2p(x_2)dx_2=E[X_2]$が成り立つので
E[X_1 X_2]=E[X_1]E[X_2]
「積の期待値」が「期待値の積」で表せることが示されました。
共分散
前置きが長くなりましたが、共分散の解説に入ります。
以下の順番で解説します。
・共分散の定義
・2次元正規分布と共分散
・多次元正規分布と共分散
・共分散と相関係数
・共分散の性質
共分散の定義
まずは共分散の定義を解説します。
分散の定義を多変数に拡張し、和の分散を考えることで、共分散を導き出す事ができます。
多変数確率分布における分散
多変数の分散は、1変数の分散の式の期待値を、多変数の期待値で置き換えたものとなります。
V[f(\boldsymbol{x})]=E \Bigl[\bigl(f(\boldsymbol{x})-E[f(\boldsymbol{x})]\bigr)^2 \Bigr]
例えば、各確率変数の分散$V[X_n]$(狭義の分散)は、以下のように求めます
V[X_n]=E \Bigl[\bigl(X_n-E[X_n]\bigr)^2 \Bigr]
和の分散
2つの確率変数の和の分散を考えます。
(式変形には期待値の加法性を使用します)
V[X_1+X_2]=E\Bigl[\bigl(X_1+X_2-E[X_1+X_2]\bigr)^2 \Bigr]\\
=E\Bigl[\bigl(X_1+X_2-E[X_1]-E[X_2]\bigr)^2 \Bigr]\\
=E\Bigl[\bigl((X_1-E[X_1])+(X_2-E[X_2])\bigr)^2 \Bigr]\\
=E\Bigl[(X_1-E[X_1])^2+(X_2-E[X_2])^2 + 2(X_1-E[X_1])(X_2-E[X_2]) \Bigr]\\
=E\bigl[(X_1-E[X_1])^2 \bigr] + E\bigl[(X_2-E[X_2])^2 \bigr] + E\bigl[2(X_1-E[X_1])(X_2-E[X_2]) \bigr]\\
=V[X_1]+V[X_2] + 2E\bigl[(X_1-E[X_1])(X_2-E[X_2]) \bigr]
上記の式を見ると、以下の3つの成分に分けられる事がわかります。
\left\{\begin{array}{ll}
V[X_1] \cdots X_1のみに依存する成分 \\
V[X_2] \cdots X_2のみに依存する成分 \\
E\bigl[(X_1-E[X_1])(X_2-E[X_2]) \bigr] \cdots X_1とX_2両方に依存する成分\\
\end{array}\right.
※最後の成分は2で割っていることにご注意ください
このうち3つ目の「X1とX2両方に依存する成分」を共分散と呼び、$Cov[X_1,X_2]$と表記します。
共分散の定義
以上まとめると、共分散$Cov[X_1,X_2]$は期待値Eを使って以下のように定義できます。
Cov[X_1,X_2]=E\bigl[(X_1-E[X_1])(X_2-E[X_2]) \bigr]
この式だけだと共分散の存在意義がイマイチ分からないと思うので、直感的なイメージや具体的な活用例を交えて解説を進めます。
共分散の直感的なイメージ
共分散の式を見ると、$(X_1-E[X_1])(X_2-E[X_2])$の期待値、すなわち全定義域での確率密度とのたたみ込み積分
Cov[X_1,X_2]=E\bigl[(X_1-E[X_1])(X_2-E[X_2]) \bigr]\\
=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} p(x_1, x_2)(x_1-E[X_1])(x_2-E[X_2])dx_1 dx_2
で表されることが分かります。
上式の$(x_1-E[X_1])(x_2-E[X_2])$の部分に着目すると、下図のように重心(各変数の期待値)(E[X1], E[X2])を基準に左下から右上方向が正、右下から左上方向が負となることが分かります。
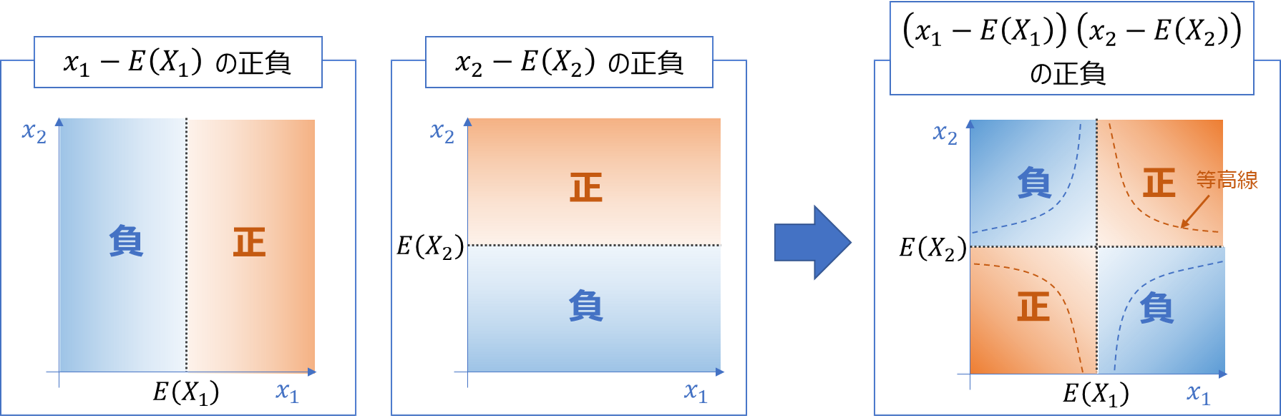
上記を踏まえると、確率密度$p(x_1, x_2)$とのたたみ込みである共分散は
・左下から右上方向の確率密度が高いと正
・右下から左上方向の確率密度が高いと負
となり、確率分布の斜め方向の偏在、すなわち2変数の相関と関連した指標となることが分かります。
これは冒頭の散布図におけるイメージとも一致するかと思います。
共分散と相関係数
共分散は2変数の相関を表しますが、変数のスケールが規格化されていないため、相関の強さだけでなく、変数のスケールも値の大きさに影響を与えてしまいます。
よって異なる確率分布(またはデータセット)での結果を比較することはできません。
そこで各変数の分散の幾何平均$\sqrt{V[X_1]V[X_2]}$で割って規格化することで変数のスケールの影響を排除(変数を標準化してから共分散を求めることに相当)し、純粋な相関の強さを評価できるようにした指標を相関係数と呼びます。
これにより異なるデータセットでの結果を比較できるようになります。
相関係数\rho[X_1,X_2]=\frac{Cov[X_1,X_2]}{\sqrt{V[X_1]V[X_2]}}
相関係数の詳細については、以下の記事で解説しております
共分散の基本性質
共分散が満たす重要な性質を解説します
共分散の対称性
共分散は、添字を反転させても値が等しくなります
Cov[X_1,X_2]=E\bigl[(X_1-E[X_1])(X_2-E[X_2]) \bigr]\\
=E\bigl[(X_2-E[X_2])(X_1-E[X_1]) \bigr]\\
=Cov[X_2,X_1]
共分散の計算法
共分散を計算しやすいよう、以下のような式変形がよく行われます
Cov[X_1,X_2]=E\bigl[(X_1-E[X_1])(X_2-E[X_2]) \bigr]\\
=E\bigl[X_1X_2-X_1E[X_2]-X_2E[X_1]+E[X_1]E[X_2] \bigr]\\
=E[X_1X_2]-E[X_1E[X_2]]-E[X_2E[X_1]]+E[E[X_1]E[X_2]]\\
E[X1]やE[X2]は定数なので、以下の公式を適用すると
・定数cの期待値E[c]=c
・定数c倍の期待値E[cX]=cE[X]
=E[X_1X_2]-E[X_2]E[X_1]-E[X_1]E[X_2]+E[X_1]E[X_2]\\
=E[X_1X_2]-E[X_1]E[X_2]
共分散と独立変数
変数X1とX2が独立のとき、共分散$Cov[X_1,X_2]=0$となります。
- 証明
Cov[X_1,X_2]=E\bigl[(X_1-E[X_1])(X_2-E[X_2]) \bigr]\\
前節の式変形より
=E[X_1X_2]-E[X_1]E[X_2]
X1とX2が独立のとき、積の期待値$E[X_1X_2]=E[X_1]E[X_2]$が成り立つので、
=E[X_1][X_2]-E[X_1]E[X_2]\\
=0
なお、逆に共分散$Cov[X_1,X_2]=0$のとき、変数X1とX2が独立とは限らない(参考)ことにご注意ください
定数倍の共分散
変数を定数倍した際の共分散には、以下の関係が成り立ちます
Cov[aX_1,bX_2]=E\bigl[(aX_1-E[aX_1])(bX_2-E[bX_2]) \bigr]\\
=E\bigl[(aX_1-aE[X_1])(bX_2-bE[X_2]) \bigr]\\
=E\bigl[ab(X_1-E[X_1])(X_2-E[X_2]) \bigr]\\
=abE\bigl[(X_1-E[X_1])(X_2-E[X_2]) \bigr]\\
abCov[X_1,X_2]
共分散と分散の加法性
共分散がゼロの時、分散の加法性
V[X_1+X_2]=V[X_1]+V[X_2]
が成り立ちます。
- 証明
和の分散は、以下のように個々の分散と共分散の和で表されます。
V[X_1+X_2]=V[X_1]+V[X_2]+2Cov[X_1,X_2]
共分散がゼロの時、最後の項$2Cov[X_1,X_2]=0$となるので、
V[X_1+X_2]=V[X_1]+V[X_2]
逆に共分散がゼロでないとき、分散の加法性は成り立ちません。
分散の加法性の実用上の意義
よく、工業における誤差の評価などで、「和の標準偏差は個々の標準偏差の√二乗和となる」すなわち
\sigma[X_1+X_2]=\sqrt{\sigma[X_1]^2+\sigma[X_2]^2}
という公式が使用されます。
この式、実は分散の加法性を変形しただけです。
\sigma[X_1+X_2]=\sqrt{V[X_1+X_2]}\\
=\sqrt{V[X_1]+V[X_2]}\\
=\sqrt{\sigma[X_1]^2+\sigma[X_2]^2}
よって和をとる変数同士が独立でないと成り立ちません(和の標準偏差が√二乗和よりも大きくなる)
公式を適用する前に、相関係数や散布図等で変数同士が独立となっているかを確認しましょう
多次元正規分布と共分散
共分散が実用上で威力を発揮するのが、多次元正規分布の表現です。
多次元正規分布は多くの機械学習アルゴリズム(ナイーブベイズ分類器、マハラノビスタグチ法、混合ガウスモデル等)で活用される確率分布であり、特に教師なし学習においては最重要理論の一つと言える存在です。
多次元正規分布と共分散の関係については、以下の別記事でまとめました。
かなり長いですが、その分共分散に関する知識が深まると思うので、ぜひご一読頂ければと思います。
実データでの共分散の求め方
前述のように、現実世界では有限のデータ(サンプル=標本データ)しか観測できないため、確率分布の形状を知るためには限られたサンプルから推定する必要があります。
正規分布においては、平均ベクトルμと分散共分散行列Σ、すなわち各変数の平均、分散、共分散を推定する必要があります。
2次元データでの算出例
2次元正規分布(確率変数$X_1, X_2$からなる)を例に、これらの値を求めてみます。
サンプル数をnとし、各サンプルの(x1,x2)の値を$(x_{11},x_{21}),(x_{12},x_{22}),\cdots(x_{1n},x_{2n})$とします。
平均
サンプルから求めた平均を「標本平均」と呼びます。
以下のように、全サンプルの総和をサンプル数で割ります(母平均の定義と同じ)
\bar{x_1}=\sum_{i=1}^{n}\frac{x_{1i}}{n}\\
\bar{x_2}=\sum_{i=1}^{n}\frac{x_{2i}}{n}
分散
サンプルから求める分散には「標本分散」と「不偏標本分散」の2種類があります。
・標本分散
サンプルから母分散の定義と同じ以下の式で求めた分散を、「標本分散」と呼びます。
S_1=\sum_{i=1}^{n}\frac{(x_{1i}-\mu_1)^2}{n}\\
S_2=\sum_{i=1}^{n}\frac{(x_{2i}-\mu_2)^2}{n}
※標本分散は大文字のSで表されることが多いです。
標本分散の問題として、$期待値E(s_1)が真の母分散σ_1と比べて\frac{n-1}{n}$倍となってしまうことが挙げられます。
(証明は以下のサイトをご参照ください)
・不偏標本分散
上記の問題を解決し、期待値が母分散と等しくなるように分母をn-1で置き換えた標本分散を、「不偏標本分散」と呼びます
s_1=\sum_{i=1}^{n}\frac{(x_{1i}-\mu_1)^2}{n-1}\\
s_2=\sum_{i=1}^{n}\frac{(x_{2i}-\mu_2)^2}{n-1}
※不偏標本分散は小文字のsで表されることが多いです。
標本分散と不偏標本分散どちらを使用するか
どちらを使用しても間違いではないのですが、「母分散を偏りなく推定する(期待値が母分散と等しくなる=不偏推定量である)」という観点で、不偏標本分散が使用されることが多いです。
共分散
共分散をサンプルから求める際にも、n-1で割った「不偏標本共分散」と、nで割った(不偏でない)「標本共分散」の違いに注意が必要です。
ここでも、期待値が母集団の共分散と等しくなるよう、不偏推定量である「不偏標本共分散」を使用します。
c_{12}=c_{21}=\sum_{i=1}^{n}\frac{(x_{1i}-\mu_1)(x_{2i}-\mu_2)}{n-1}
サンプルから求めた2次元正規分布
上記の推定量を使用して、平均ベクトルμおよび分散共分散行列Σは、以下のように求まります。
\boldsymbol{\mu}=
\left(\begin{array}{c}
\bar{x_1} \\
\bar{x_2} \\
\end{array}\right)
\boldsymbol{\Sigma}=
\begin{pmatrix}
s_1 & c_{12} \\
c_{12} & s_2
\end{pmatrix}
2次元正規分布の確率密度関数p(x)は、μおよびΣを使用して以下のように求まります。
p(\boldsymbol{x})=\frac{1}{2\pi}\frac{1}{|\boldsymbol{\Sigma}|^\frac{1}{2}}\exp\bigl(-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^T\boldsymbol{\Sigma}^{-1}(\boldsymbol{x}-\boldsymbol{\mu})\bigr)
前述のように、上記パラメータはあくまでサンプルから「推定」された値であり、(頻度論における)真の値からは誤差が生じることにご注意ください(特にサンプルが少ないときは誤差が大きくなります)
※ なお、以下の英語版Wikipediaでは分散共分散行列を最尤推定およびベイズ推定で求める例が紹介されています。興味がある方はご参照ください
サンプルにまつわる推定・検定
サンプルから求められた共分散(標本共分散)が、真の値(母共分散)に対してどの程度信頼性があるかを求める手法が、推定・検定です。
ただし、共分散自体の検定・推定はほとんど行われることはありません。
むしろ使い勝手の観点から共分散を規格化した「相関係数」に関して検定・推定が行われる事が多く、その中でも「無相関の検定」や「フィッシャーのz変換」は非常にポピュラーな手法です。
これらについては現在記事にまとめておりますので、しばしお待ちいただければと思います。
共分散まとめ
以上共分散について重要事項をまとめると、以下のようになります
・x1とx2の共分散は$Cov[x_1,x_2]=E\bigl[(x_1-E[x_1])(x_2-E[x_2]) \bigr]$と定義される
・共分散$Cov[x_1,x_2]$は、和の分散のうち「x1とx2両方に依存する成分」を表す
・共分散は、左下から右上方向の確率密度が高いと正、右下から左上方向の確率密度が高いと負となる、2変数の相関と関連した指標
・サンプルから求まる共分散の不偏推定量は、$\sum_{i=1}^{n}\frac{(x_{1i}-\mu_1)(x_{2i}-\mu_2)}{n-1}$(分母がn-1であることに注意)
・共分散は、実用上において多次元正規分布の表現や主成分分析、教示なし学習等の機械学習手法に活用できる
参考文献
・統計学入門 東京大学出版会
・パターン認識と機械学習 上 丸善出版
※以下の資料も参考にさせて頂きました
