強化学習の基本を図と数式で理解する①

0. はじめに

今年大学のTAとして、学部1年生向けに強化学習の入門授業のようなものを担当しました。
実質的な授業回数は3回程度なので、本当に触り程度ですが、せっかく資料を作成しましたので公開しようと思います。

記事は、内容に即して第1回と第2回に分けてあります。
第1回の本記事では、強化学習の理論的背景を図と数式を交えて解説します。
第2回では、古典的な強化学習の一つであるQ学習について解説し、実際にpythonを用いて迷路踏破Agentを実装します。
第２回で実装したAgentのコードもこちらで公開しています。

なるべく初学者でもわかりやすいように書いていますが、見づらい部分やわかりにくい部分、間違っている箇所などありましたらご指摘くださるとありがたいです。
なお本記事は、強化学習 Advent Calendar 2021 の19日目の記事です。

1. 強化学習の概要

• 機械学習の大きな分類（教師あり学習、教師なし学習、強化学習）の一つ
• 犬をしつけるときのように、良いことをしたらご褒美を、悪いことをしたら罰を与えて学習させる
• ゲームAIやロボット制御によく使われる

1.1 強化学習の位置づけ

強化学習は機械学習の一種である。機械学習は、以下の3つに大別される。これは昨今様々なところで耳にする「ディープラーニング」であるとは限らない。各手法でディープニューラルネットワークを使うか否かは、また別の話ということに注意。今回は強化学習をメインに扱うのであまり深入りはしないが、各手法は以下のように説明されることが多い。

教師あり学習

データ$\ x_i \ $とラベル$\ t_i \ $のペアを$\ n \ $個用意し、ある関数$\ F \ $の出力$\ F(x_i) \ $が対応するラベル$\ t_i \ $と近くなるように、関数$\ F \ $の係数を学習する手法。

教師なし学習

データ$\ x_i \ $を$\ n \ $個用意し、そのデータの構造に着目することでその確率分布$\ P(x) \ $を学習する手法。

強化学習

データは用意しなくて良い。環境との相互作用によって得られる報酬$\ r \ $の総和が最大になるような方策$\ \pi \ $を学習する手法

こうしてみると、強化学習を理解するためには、まず環境、報酬、方策といった単語の理解が必要だということが分かる。次節ではこの3つのキーワードと共に強化学習がどのような「学習」なのかを具体的に見ていく。

1.2 環境・報酬・方策のイメージ

ここでは、数式なしで直感的に理解をしてもらうことを目指す。
結論から書くと、強化学習の文脈において

環境

学習者（エージェントと呼ぶことが多い）が存在し行動する外界のこと。学習者（エージェント）に対して報酬を与えたり、現在の周囲の状態を教えてくれる

報酬

学習者（エージェント）が自身の行動の良し悪しを判断するために用いる、外部からの信号のこと

方策

学習者（エージェント）が環境の状態を受けてどのような行動をとるかを決定する指針のこと

である。といってもこれではイメージが湧かないと思うので、以下に3つの例を載せた。

例1 犬のしつけ

犬におすわりをしつけることを考える。飼い主が「おすわり」と命令すると、犬は飼い主の所作や声を知覚して座るか座らないかの判断をする。ちゃんと座ることができたらおやつをあげることで、犬は「おすわり」と言われた時に座るといいことがあると学習していく。

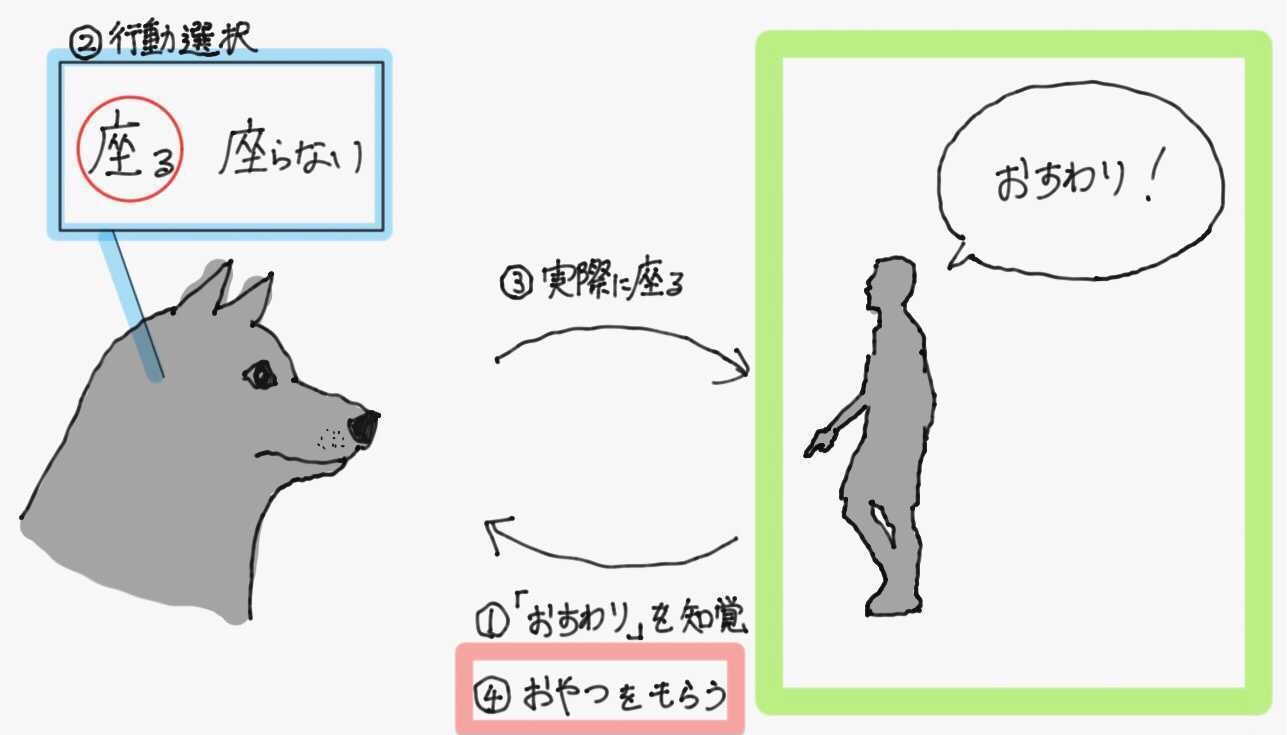
この場合の環境・報酬・方策は以下の通り。

環境

犬（エージェント）におやつをあげる飼い主が存在し、犬が行動（歩く、走る、トイレする、おすわりする、伏せる、etc...）できる空間

報酬

おやつ

方策

犬の脳（飼い主からの「おすわり」を受けて、実際に座るか座らないかを決定する）

例2 子供のしつけ

今度は子供に勉強をさせることを考える。親が「勉強しなさい」というと、子供はそれを見聞きして勉強をするかしないかの判断をする。勉強をせずにゲームばかりしていると親に叱られるため、子供は「勉強しろ」と言われたら指示に従わないと嫌なことが起きると学習していく。

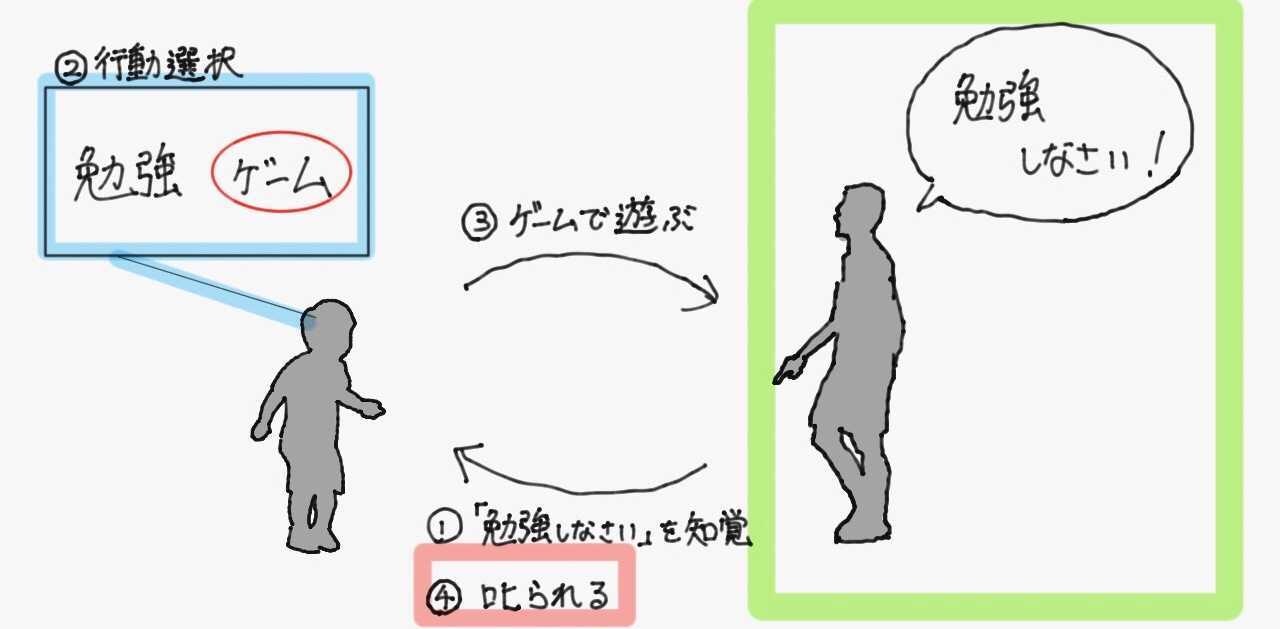
この場合の環境・報酬・方策は以下の通り。

環境

子供（エージェント）を叱る親が存在し、子供が行動（宿題をする、ゲームをする、食べる、etc...）できる空間

報酬

親の叱責（負の報酬＝罰というイメージ）

方策

子供の脳（親からの「勉強しなさい」を受けて、実際に勉強するかしないかを決定する）

例3 ロボットの迷路踏破

最後に、同様の手順でロボットに迷路を踏破させることを考える。ロボットはセンサによって自身の位置を取得し何らかの行動選択をするとして、スタートからゴールにたどり着くように学習させる。前述の二つの例から、各マスでの行動が望ましいものならば正の、望ましくないものならば負の報酬を与えることができれば、その報酬を最大化するように行動を修正していけばロボットはいずれ迷路を踏破することができるようになる

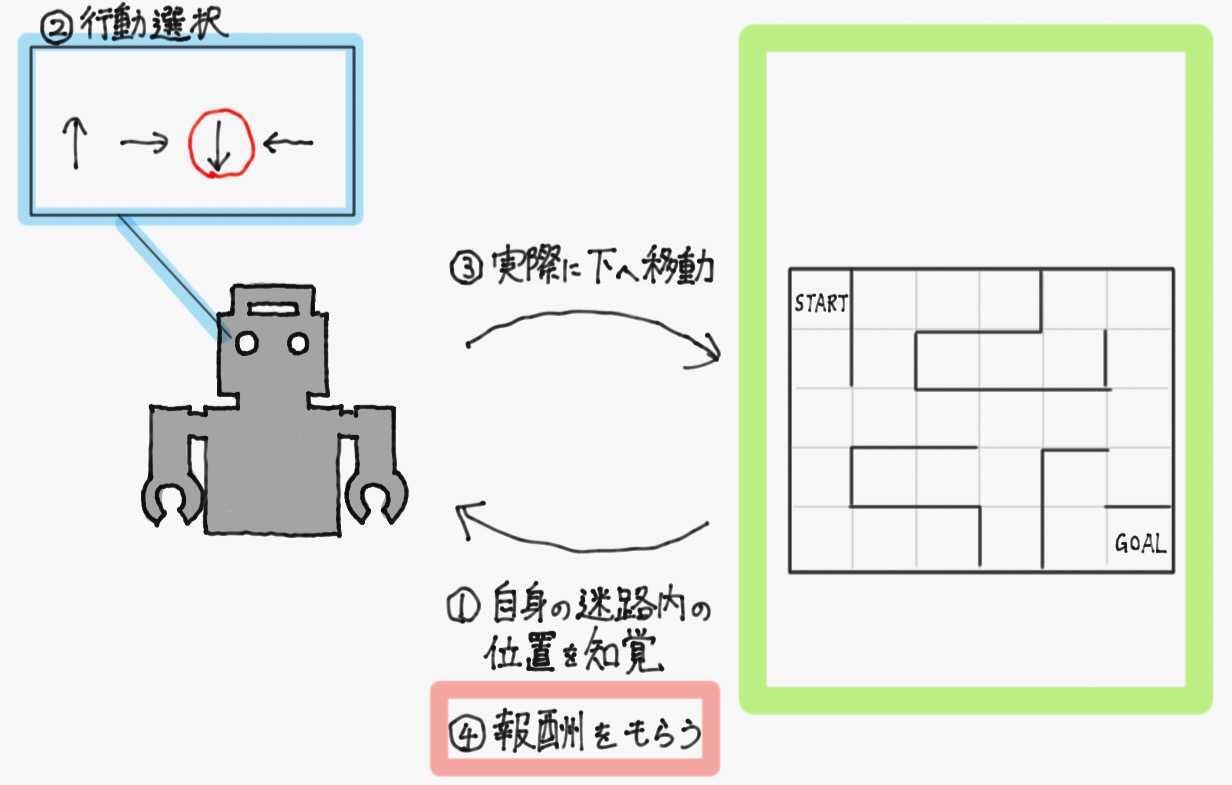
この場合の環境・報酬・方策は以下の通り。

環境

ロボット（エージェント）が内部を散策でき、とった行動に対して報酬を与えてくれる迷路自体

報酬

ロボットの望ましい行動（ゴールするなど）に対しては正の数値、望ましくない行動（壁に向かって行こうとするなど）に対しては負の数値

方策

迷路内での自身の位置をもとに、上下左右どちらに行動するか決める関数

このように強化学習とは、環境から得られる情報をもとに行動を決定し、得られる報酬がより多くなるように行動を修正していく学習手法である。
以降の章では、上記の迷路の例を用いて数学的に強化学習を定義していく。

2. 強化学習の定式化

• 強化学習に必要な事前知識として、確率変数と期待値について説明する
• 迷路の例を用いて、強化学習を数学的に定義していく
• 強化学習の中核を成す方程式である、Bermann方程式を導出する

2.1 必要な事前知識

強化学習を数式で記述していくにあたって、必要となる事前知識について解説する。

2.1.1 確率変数

確率的にその値が決定する変数のことを、確率変数という。

高校までは「変数」といったら「そこに（何か制約条件がない限り）任意の数値を入れてもよい何か」という意味しか持たなかった。

一方、確率変数はそこに入ってくる任意の数値がそれぞれどれぐらいの確率で実現しうるかということも考慮に入れた概念である。

例えば、サイコロの出目を考えるとしよう。

高校までで習った普通の変数を使うと、サイコロの出目の値は$\ x \ $と置ける。

x = 
\begin{cases}
  1\\
  2\\
  3\\
  4\\
  5\\
  6
\end{cases}

この時、もちろん$\ x \ $はサイコロの出目としてとりうる値（1,2,3,4,5,6）は全て一般化して表すことができているが、その値がどれぐらいの確率で実現するかに関しては何も表せていない。

確率変数を使うと、サイコロの出目は$\ X \ $と表せ（確率変数は変数名に大文字斜体を用いるのが普通）、それぞれの値が実現する確率も考慮される。

X =
\begin{cases}
  1 & \bigl( \ \text{実現確率は}1/6 \ \bigr) \\
  2 & \bigl( \ \text{実現確率は}1/6 \ \bigr) \\
  3 & \bigl( \ \text{実現確率は}1/6 \ \bigr) \\
  4 & \bigl( \ \text{実現確率は}1/6 \ \bigr) \\
  5 & \bigl( \ \text{実現確率は}1/6 \ \bigr) \\
  6 & \bigl( \ \text{実現確率は}1/6 \ \bigr)
\end{cases}

この時、確率変数$\ X \ $が実現値$\ x \ $をとる確率は$\ \mathrm{Pr}(X=x) \ $と記述される。（例：$\mathrm{Pr}(X=1)=1/6$）
確率変数の実現値を横軸に、その実現確率を縦軸にしてプロットしたグラフを確率分布と呼び、代表的なものには名前がついている。

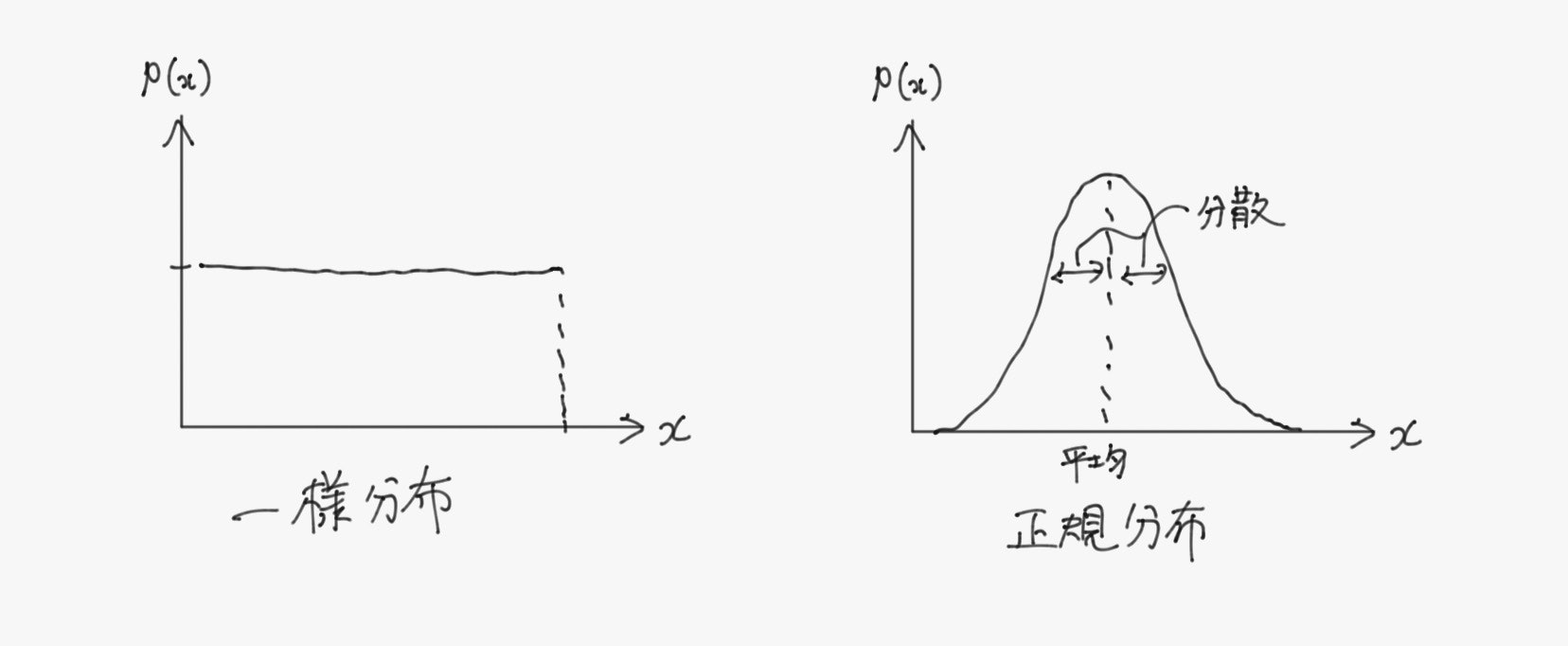
また、確率変数$\ X \ $が確率分布$\ p \ $に従うとき、$X \sim p$とかく。

2.1.2 期待値

ある確率変数$\ X \ $が平均的にどのような値を取るか、その確率も考慮して計算した値のことを、期待値という。確率変数$\ X \ $の期待値$\underset{X \ \sim \ \Pr(X)}{\mathbb{E}} [X]$は次式で定義される。

\underset{X \ \sim \ \Pr(X)}{\mathbb{E}} [X]
\triangleq
\sum_x x \cdot \mathrm{Pr}(X=x)

例として、1と2が他の目よりも出やすい歪なサイコロを考える。

出目の確率変数を$\ X \ $として、$\ X \ $は次のように定義されるとする。

X \triangleq
\begin{cases}
  1 & \bigl( \ \mathrm{Pr}(X=1)=1/4 \ \bigr) \\
  2 & \bigl( \ \mathrm{Pr}(X=2)=1/4 \ \bigr) \\
  3 & \bigl( \ \mathrm{Pr}(X=3)=1/8 \ \bigr) \\
  4 & \bigl( \ \mathrm{Pr}(X=4)=1/8 \ \bigr) \\
  5 & \bigl( \ \mathrm{Pr}(X=5)=1/8 \ \bigr) \\
  6 & \bigl( \ \mathrm{Pr}(X=6)=1/8 \ \bigr)
\end{cases}

このとき、確率を考慮しない普通の平均値$\ \bar{x} \ $は、

\bar{x}=\frac{1+2+3+4+5+6}{6} = 3.5

と$1 \sim 6$のちょうど中央値だが、これはこのサイコロを振って出ると予想される値としてはふさわしくない。（$1,2$の目が出やすいのだから、$3.5$より小さい値が平均的に得られると予測すべき）

ここで、$\ X \ $の期待値を考えると、

\underset{X \ \sim \ \Pr(X)}{\mathbb{E}} [X]
=
\frac{1}{4} \cdot 1
+
\frac{1}{4} \cdot 2
+
\frac{1}{8} \cdot 3
+
\frac{1}{8} \cdot 4
+
\frac{1}{8} \cdot 5
+
\frac{1}{8} \cdot 6
=
3

となり、分布の偏りを考慮した推定値が算出できている。

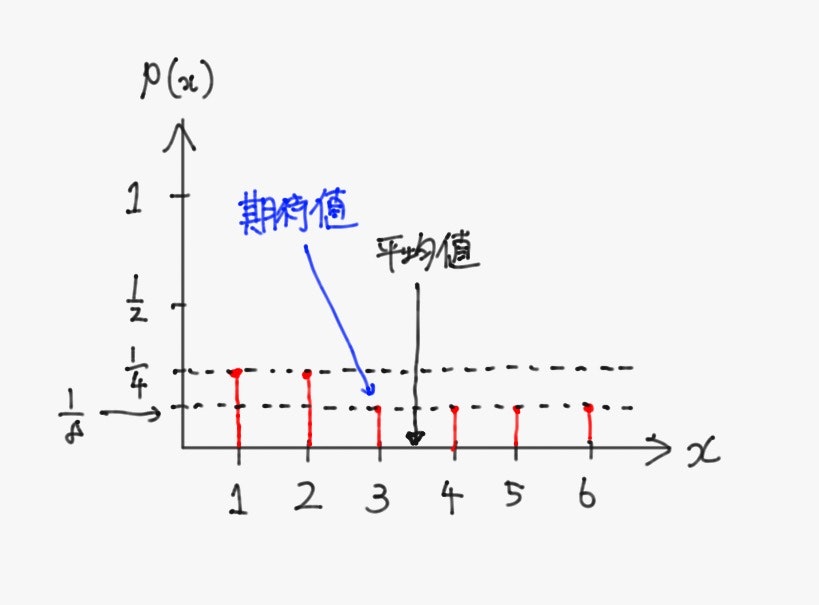
ちなみに、確率変数が一様分布に従う（取りうる値が全て等確率で実現する）場合や、正規分布に従う場合には平均値と期待値は一致する。

2.1.3 期待値の補題

これで、強化学習の定式化に必要な最低限の知識は共有したが、追加で以降の数式変形で頻繁に用いる次の式を証明しておく。

\underset{X \ \sim \ \Pr(X)}{\mathbb{E}} [X]
=
\sum_y
\underset{X \ \sim \ \Pr(X)}{\mathbb{E}} [X \mid Y] 
\cdot
\mathrm{Pr}(Y=y)

ここで、中棒$(\ \mid \ )$は条件を表しており、例えば$\ \mathrm{Pr}(A=a \mid B=b)\ $は確率変数$\ B \ $が実現値$\ b \ $という値を取るという条件下で、確率変数$\ A \ $が実現値$\ a \ $という値を取る条件付き確率を意味している。同様に$\ \underset{A \ \sim \ \Pr(A)}{\mathbb{E}} [A \mid B=b]\ $は、確率変数$\ B \ $が実現値$\ b \ $という値を取るという条件下での、確率変数$\ A \ $の期待値を意味している。

証明

\begin{align}
  \sum_y
  \underset{X \ \sim \ \Pr(X)}{\mathbb{E}} [X \mid Y] 
  \cdot
  \mathrm{Pr}(Y=y)
  &=
  \sum_x \sum_y
    x
    \cdot
    \mathrm{Pr}(X=x \mid Y=y)
    \cdot
    \mathrm{Pr}(Y=y)
  \qquad
  (\because \text{期待値の定義}) \\
  &=
  \sum_x \sum_y
    x
    \cdot
    \mathrm{Pr}(X=x, Y=y)
  \qquad
  (\because \text{同時確率と条件付き確率の関係}) \\
  &=
  \sum_x
    x
    \cdot
    \left(
      \sum_y
        \mathrm{Pr}(X=x, Y=y)
    \right) \\
  &=
  \sum_x
    x
    \cdot
    \mathrm{Pr}(X=x)
  \qquad
  (\because \text{周辺化}) \\
  &=
  \underset{X \ \sim \ \Pr(X)}{\mathbb{E}} [X]
  \qquad
  (\because \text{期待値の定義})
\end{align}

2.2 強化学習の数学的定義

2.2.1 第1章のおさらい

環境

学習者（エージェントと呼ぶことが多い）が存在し行動する外界のこと。学習者（エージェント）に対して報酬を与えたり、現在の周囲の状態を教えてくれる

報酬

学習者（エージェント）が自身の行動の良し悪しを判断するために用いる、外部からの信号のこと

方策

学習者（エージェント）が環境の状態を受けてどのような行動をとるかを決定する指針のこと

エージェントは環境から得た情報をもとに方策に従い行動を決定し、その結果環境から報酬と新しい情報を得る。このプロセスを繰り返し、環境から得られる報酬の和がより多くなるように方策を更新していくのが強化学習だった。

これを数学的に書き直すと、強化学習とは

1. 「状態$\ s \ $にいるエージェントが、行動$\ a \ $を選択する」ということを繰り返す逐次意思決定問題において、
2. 環境から将来的に受け取ると期待される報酬$\ r \ $の総和を最大化するように、
3. 自身の方策$\ \pi(a \mid s) \ $を更新していく

手法のことである。

2.2.2 記号の定義

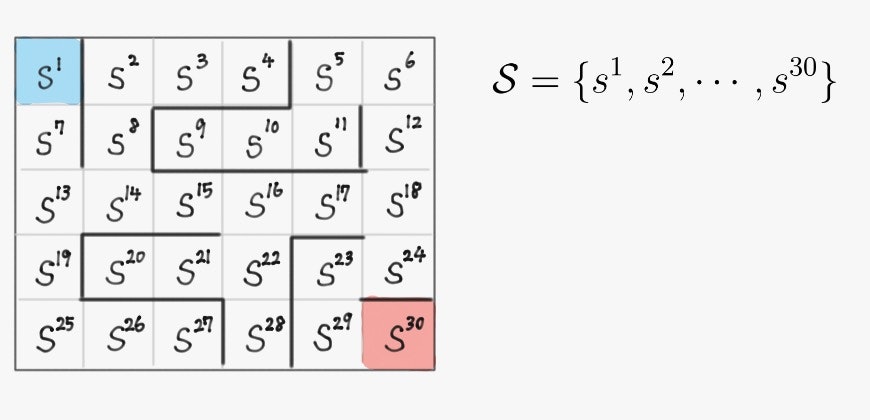
• 状態集合：$\mathcal{S}=\{s^1, s^2, \cdots, s^{\vert \mathcal{S} \vert}\}$
  環境内の全ての状態を格納した集合。

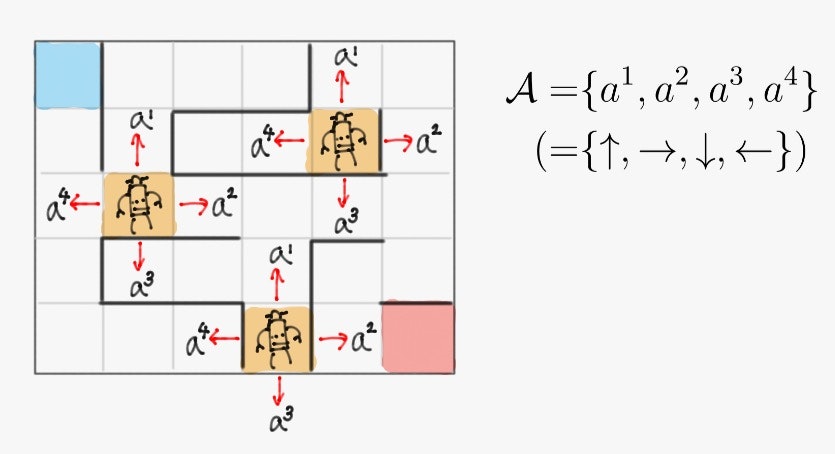
• 行動集合：$\mathcal{A} = \{a^1, a^2, \cdots, a^{\vert \mathcal{A} \vert}\}$
  エージェントが環境内でとることのできる全ての行動を格納した集合。

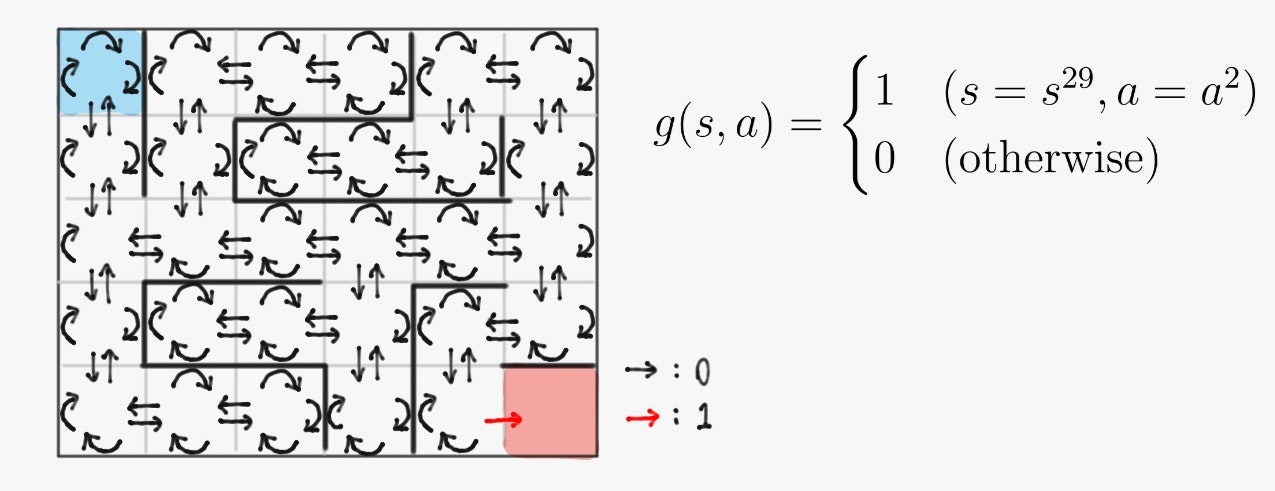
• 報酬関数：$g:\mathcal{S} \times \mathcal{A} \rightarrow \mathbb{R}$
  エージェントが状態$\ s \in \mathcal{S} \ $で行動$\ a \in \mathcal{A} \ $をとった時に、環境から得られる報酬$\ r \ $を対応づける関数。エージェントからは未知である。

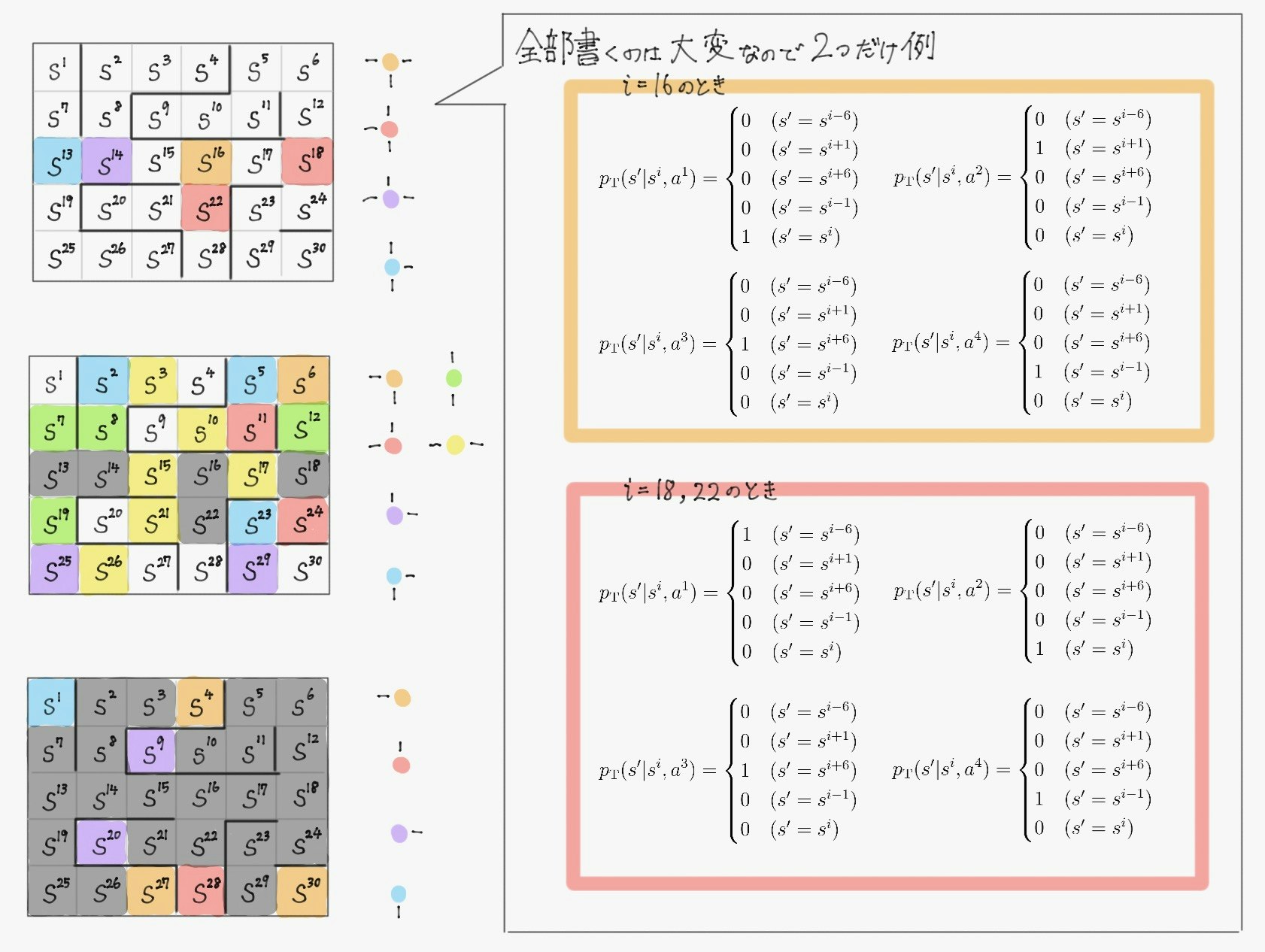
• 方策関数：$\pi:\mathcal{A} \times \mathcal{S} \rightarrow [0,1]$
  エージェントが状態$\ s \in \mathcal{S} \ $のとき、行動$\ a \in \mathcal{A} \ $をとる条件付き確率。
  時刻$t$におけるエージェントの状態、行動を表す確率変数をそれぞれ$\ S_t, A_t \ $とおくと、

\pi(a \mid s) \triangleq \mathrm{Pr} (A_t=a \mid S_t=s)

• 状態遷移関数：$\ p_{\mathrm{T}}:\mathcal{S} \times \mathcal{S} \times \mathcal{A} \rightarrow [0,1] \ $
  エージェントが状態$\ s \in \mathcal{S} \ $で行動$\ a \in \mathcal{A} \ $をとった時に、状態$\ s' \in \mathcal{S} \ $に遷移する条件付き確率。エージェントからは未知である。
  時刻$\ t \ $におけるエージェントの状態、行動を表す確率変数をそれぞれ$\ S_t, A_t \ $とおくと、

p_{\mathrm{T}}(s' \mid s,a) \triangleq \mathrm{Pr} (S_{t+1}=s' \mid S_t=s, A_t=a)

強化学習の概要図を、これらの記号を含めて改めて書き直しておく。

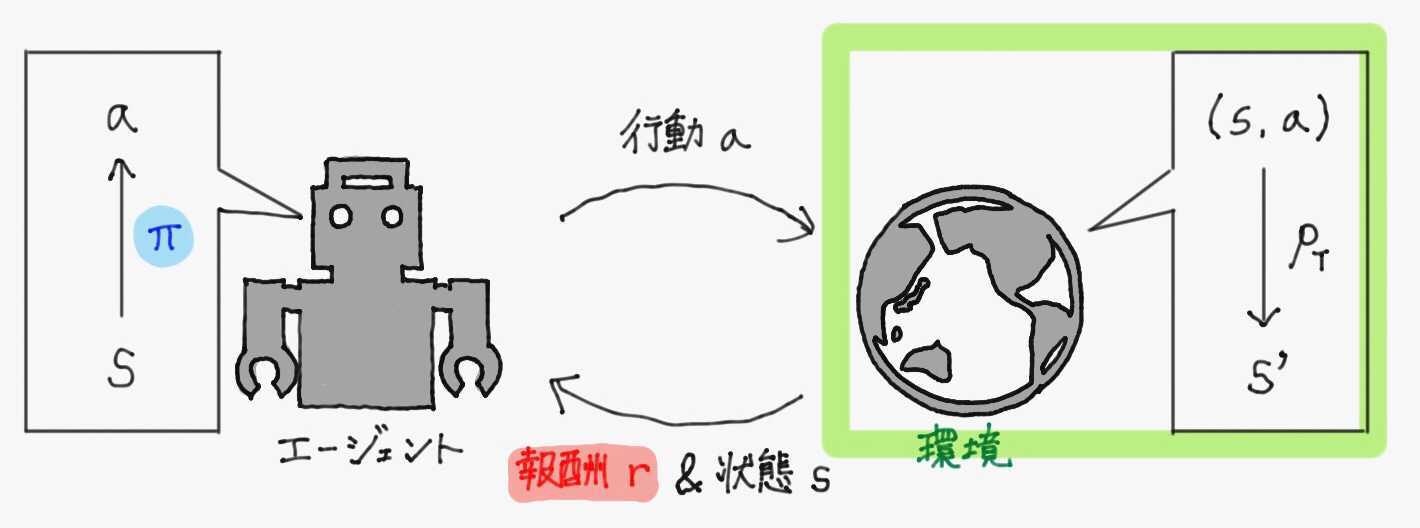
2.2.3 迷路探索の例

例として、下記のような左上にスタート、右下にゴールのある迷路を強化学習エージェントが探索する設定を考える。

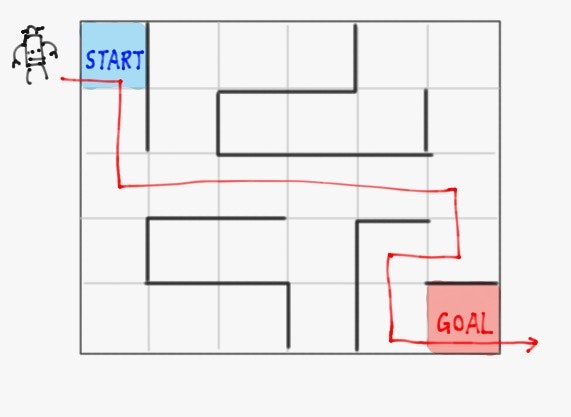
このとき、前項で導入した用語を次のように定義する。

• 状態集合
  
• 行動集合
  
• 報酬関数
  
• 状態遷移関数
  
  また、求めたい最適方策$\ \pi^*(a \mid s) \ $は、

\begin{align}
  &\pi^* \left(a \mid s^1\right)
  =
  \begin{cases}
    0 & ( a=a^1 ) \\
    0 & ( a=a^2 ) \\
    1 & ( a=a^3 ) \\
    0 & ( a=a^4 )
  \end{cases}
  &&
  \pi^* \left(a \mid s^7\right)
  &=
  \begin{cases}
    0 & ( a=a^1 ) \\
    0 & ( a=a^2 ) \\
    1 & ( a=a^3 ) \\
    0 & ( a=a^4 )
  \end{cases} \\
  &\pi^* \left(a \mid s^{13}\right)
  =
  \begin{cases}
    0 & ( a=a^1 ) \\
    1 & ( a=a^2 ) \\
    0 & ( a=a^3 ) \\
    0 & ( a=a^4 )
  \end{cases}
  &&
  \pi^* \left(a \mid s^{14}\right)
  &=
  \begin{cases}
    0 & ( a=a^1 ) \\
    1& ( a=a^2 ) \\
    0 & ( a=a^3 ) \\
    0 & ( a=a^4 )
  \end{cases} \\
  &\pi^* \left(a \mid s^{15}\right)
  =
  \begin{cases}
    0 & ( a=a^1 ) \\
    1 & ( a=a^2 ) \\
    0 & ( a=a^3 ) \\
    0 & ( a=a^4 )
  \end{cases}
  &&
  \pi^* \left(a \mid s^{16}\right)
  &=
  \begin{cases}
    0 & ( a=a^1 ) \\
    1 & ( a=a^2 ) \\
    0 & ( a=a^3 ) \\
    0 & ( a=a^4 )
  \end{cases} \\
  &\pi^* \left(a \mid s^{17}\right)
  =
  \begin{cases}
    0 & ( a=a^1 ) \\
    1 & ( a=a^2 ) \\
    0 & ( a=a^3 ) \\
    0 & ( a=a^4 )
  \end{cases}
  &&
  \pi^* \left(a \mid s^{18}\right)
  &=
  \begin{cases}
    0 & ( a=a^1 ) \\
    0 & ( a=a^2 ) \\
    1 & ( a=a^3 ) \\
    0 & ( a=a^4 )
  \end{cases} \\
  &\pi^* \left(a \mid s^{24}\right)
  =
  \begin{cases}
    0 & ( a=a^1 ) \\
    0 & ( a=a^2 ) \\
    0 & ( a=a^3 ) \\
    1 & ( a=a^4 )
  \end{cases}
  &&
  \pi^* \left(a \mid s^{23}\right)
  &=
  \begin{cases}
    0 & ( a=a^1 ) \\
    0 & ( a=a^2 ) \\
    1 & ( a=a^3 ) \\
    0 & ( a=a^4 )
  \end{cases} \\
  &\pi^* \left(a \mid s^{29}\right)
  =
  \begin{cases}
    0 & ( a=a^1 ) \\
    1 & ( a=a^2 ) \\
    0 & ( a=a^3 ) \\
    0 & ( a=a^4 )
  \end{cases}
\end{align}

となる。（上に挙げていない状態の確率値はなんでも良い）

2.2.4 割引報酬和

エージェントが最大化したいのは環境から得る報酬の総和であるが、単純に和を取るだけだと値が発散してしまう。
従って、実際には次式で定義される割引報酬和$\ C_t \ $（確率変数であることに注意）が用いられる。

C_t \triangleq \sum_{k=0}^{K-1} \gamma^k  R_{t+k}

なお$\ R_t \ $は時刻$\ t \ $における報酬$\ r \ $の確率変数。$\ \gamma \in [0,1) \ $は時間割引率と呼ばれるパラメータで、これを現時点よりも将来の時刻に得られる報酬の値に乗算していくことで、未来の価値であればあるほど不確かであることを反映している。
（以下は$\ C_0 \ $の例）

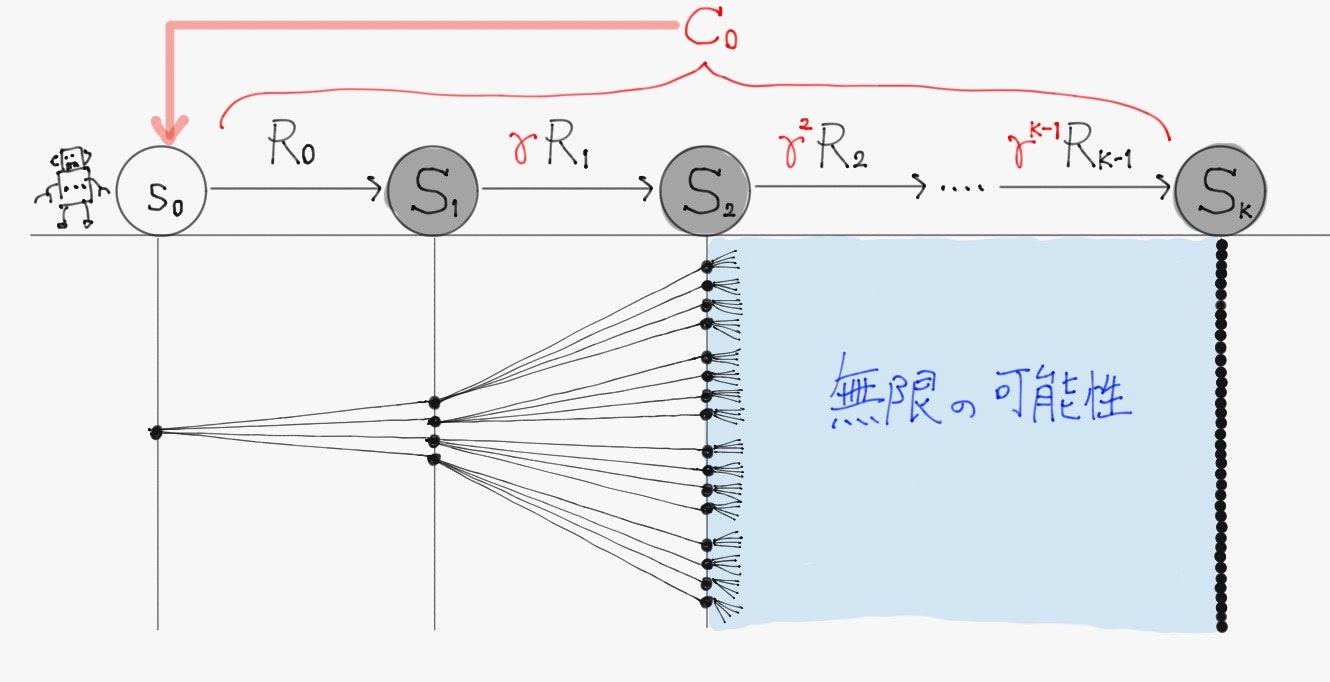
これは時刻$\ t+1 \ $における割引報酬和$\ C_{t+1} \ $を用いて、

C_t = R_{t} + \gamma C_{t+1}　\qquad -(\diamondsuit)

と漸化式のように書くこともできる。

ここでエージェントがある方策$\pi$に基づいて$\ K \ $回だけ実際に行動して、状態と行動の系列$\ \tau = {(s_0, a_0), (s_1, a_1), \cdots, (s_K, a_K)} \ $を生成すれば、各ステップで報酬$\ r_t=g(s_t,a_t) \ $が得られ、状態$\ s_0 \ $における割引報酬和$\ C_0 \ $はある実現値$\ c^* \ $をとる。

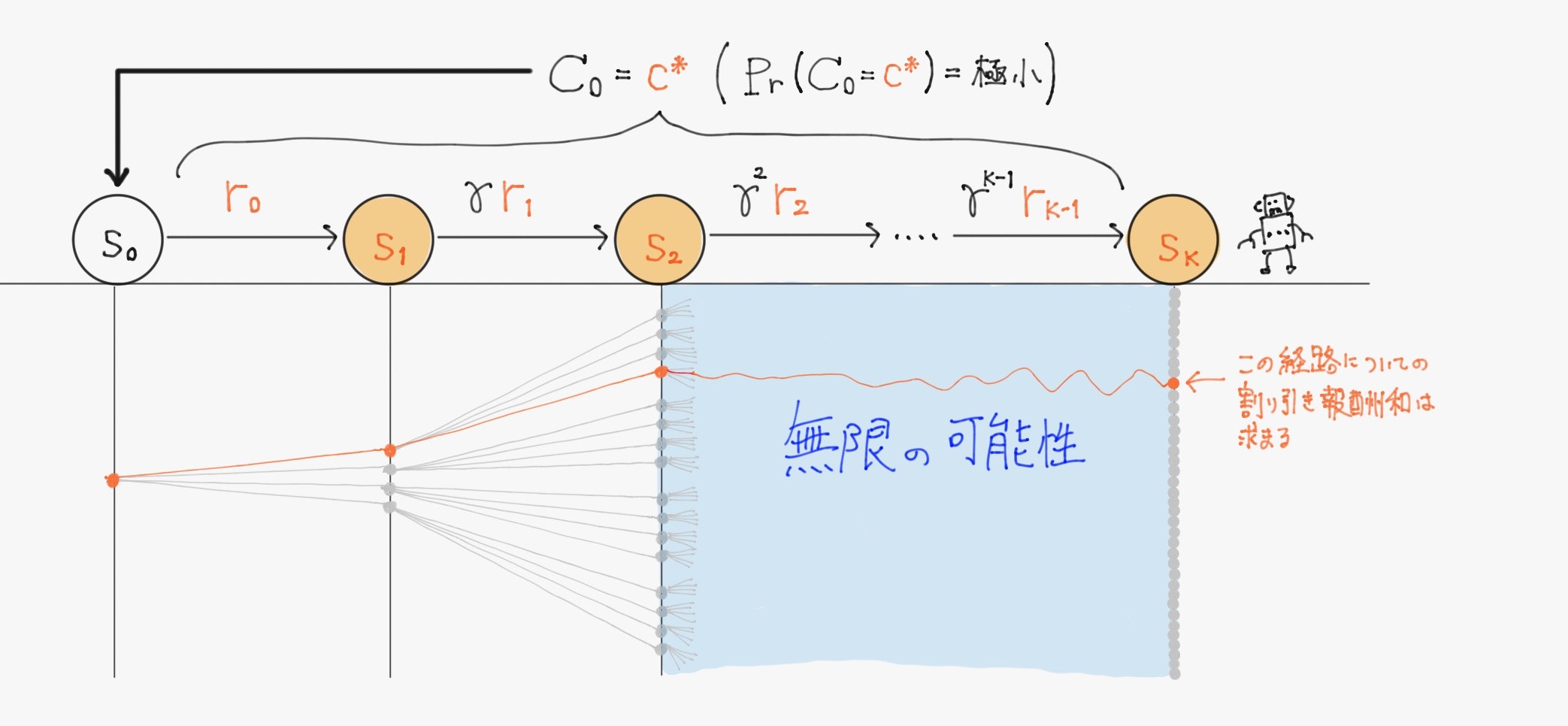
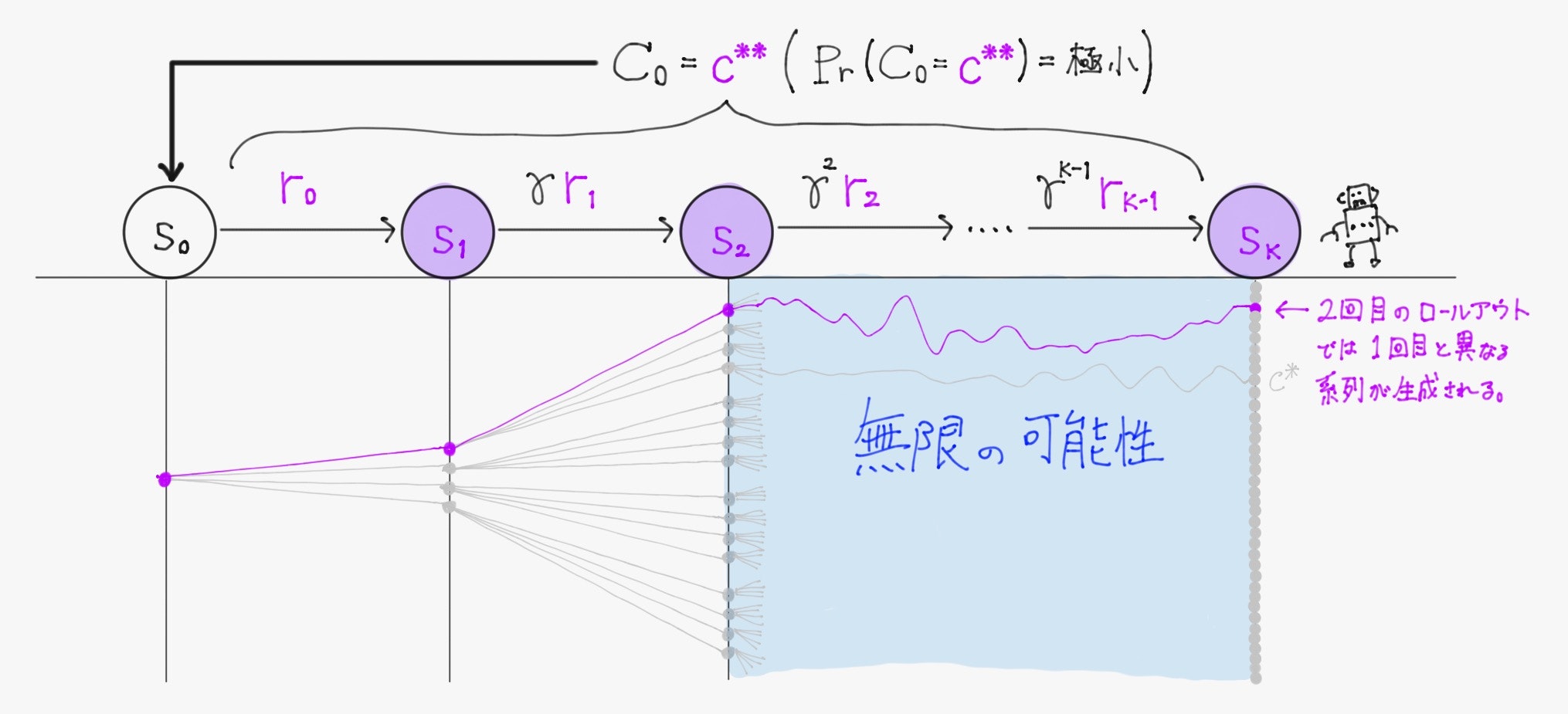
（$\ \pi \ $が確率的方策だとすれば、）再びエージェントが同じ方策に基づいて$\ K \ $回だけ行動したとしても異なる系列が生成され、もちろん得られる割引報酬和の実現値も異なる。また、方策を全く異なるものに変えて$\ K \ $回行動すれば、生成される系列及び得られる割引報酬和の実現値も変化する。
すなわち、初期状態から一定のステップ数行動することを100回やれば100通り、1000回やれば1000通りの系列が生成され、それにより得られる割引報酬和も100通り、1000通り存在するということである。

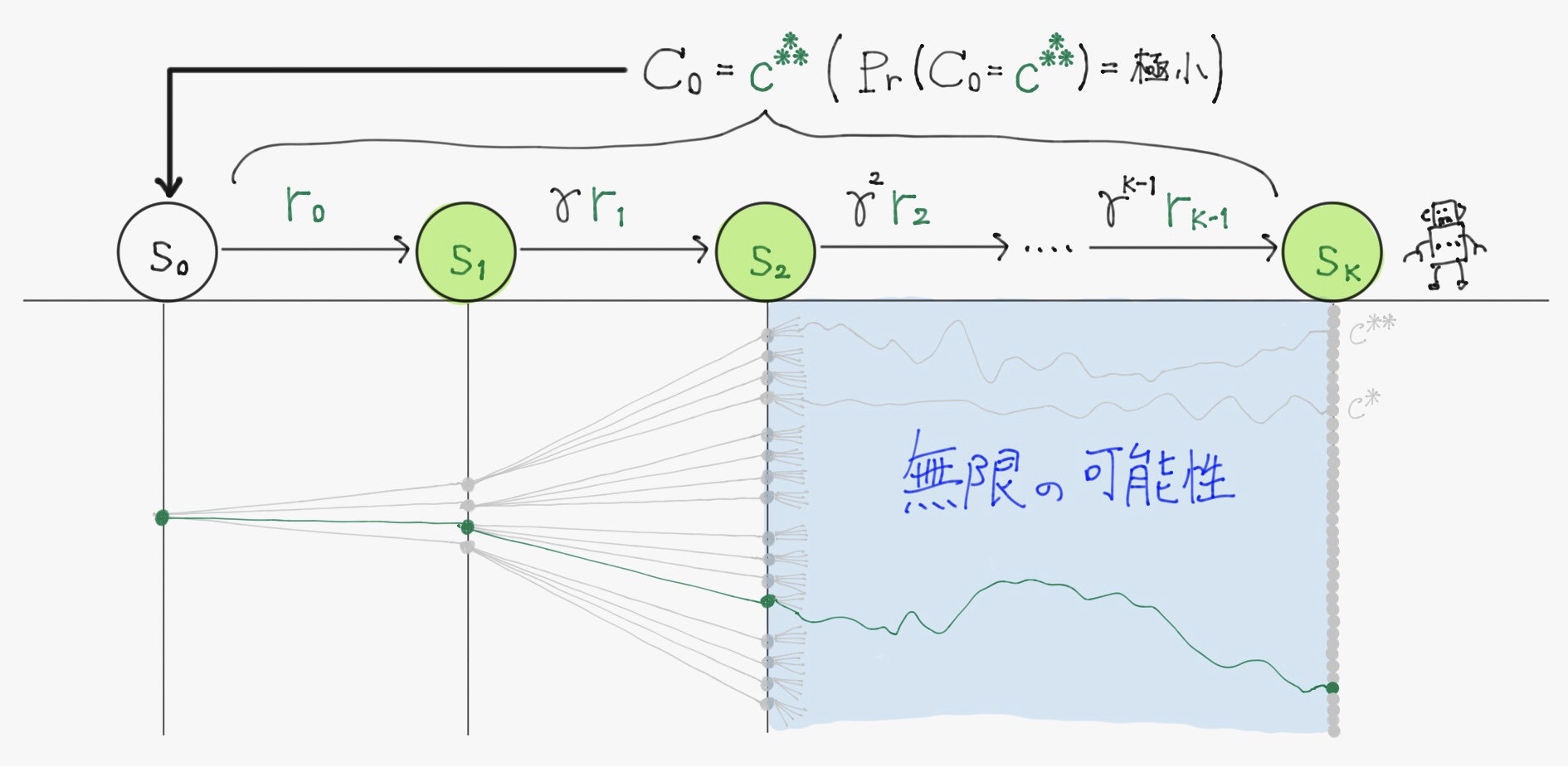
2.2.5 価値関数

ここで再び強化学習の目的を思い起こすと、

1. 環境から将来的に受け取ると期待される報酬$\ r \ $の総和を最大化するように、
2. 自身の方策$\ \pi(a \mid s) \ $を更新していく

ことだった。これを割引報酬和と系列ということばを使って書き換えると、

1. 現在の状態から生成されうる膨大な数の系列の中から割引報酬和$ \ C_t \ $が最大となる系列を見つけ
2. その系列が常に生成されるような方策$\ \pi(a \mid s) \ $を獲得する

ことである。

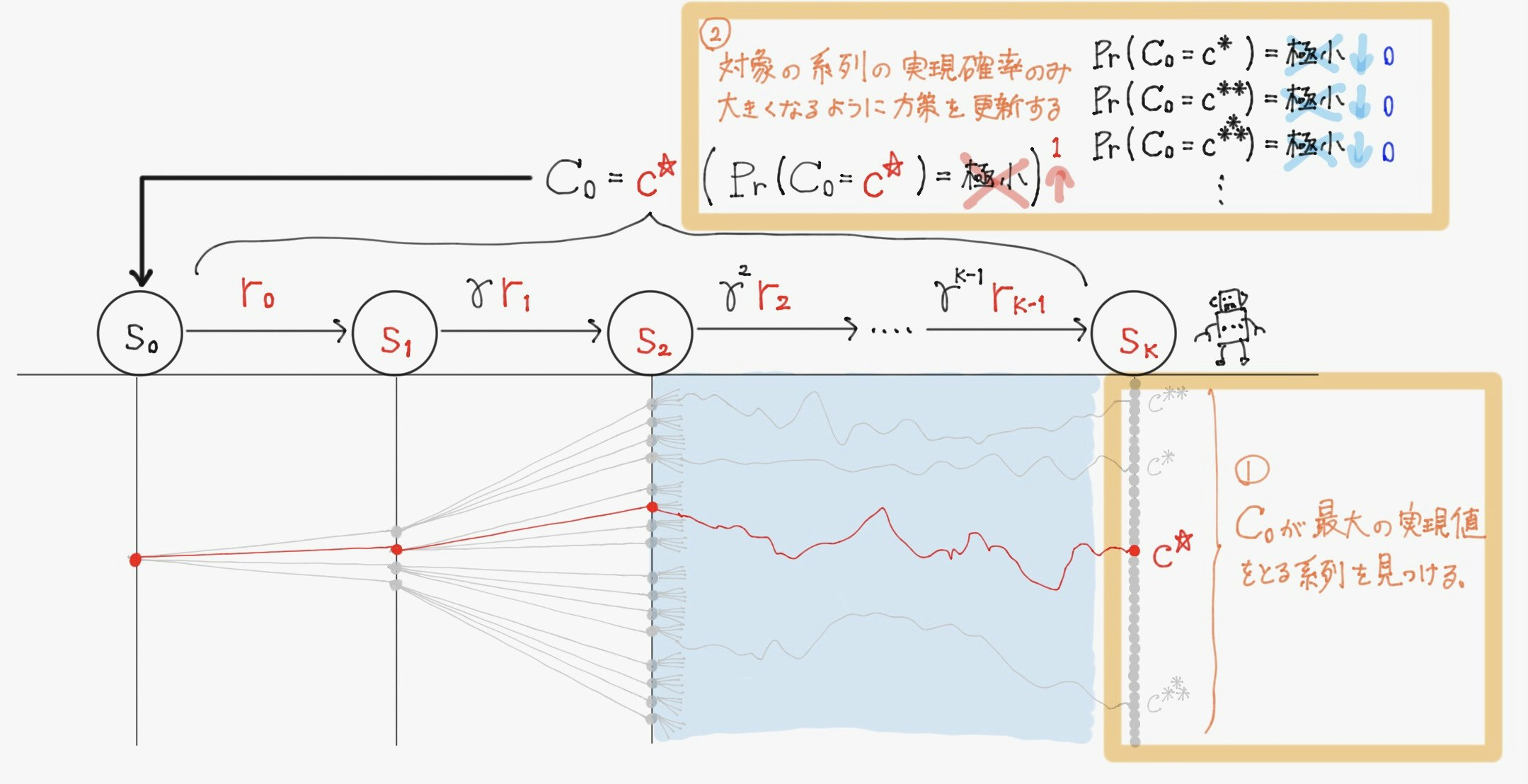
この目的を達成する最も直感的な方法は、考えうる全ての系列をエージェントが実際に行動して生成してみることである。（こうすれば割引報酬和の取りうる全ての実現値が得られ、それらを比較して最大となる系列を常に生成するような方策を最適方策とすれば良い）
ただしほとんどの場合、計算時間が無限にかかるためこの手法を取ることはできない。
従って、行動回数を計算可能な回数に抑えつつ、なるべく最適な方策を求めることが重要になる。

そこで、割引報酬和$\ C_t \ $の個々の実現値でなく、その平均値（期待値）に着目する。実現値は実際にエージェントが系列を生成しなければ得られなかったが、期待値ならば過去得られている情報を元に近似的に計算できるためである。

具体的には

1. 各状態$\ s \ $で割引報酬和$\ C_0 \ $の期待値をとりあえず近似的に計算しておき、
2. 行動時にはその値を指針としながら行動を決定しつつ、
3. 環境との相互作用を繰り返すたびに徐々に近似値を正確なものへと更新していく

ことで行動の回数を抑える。

以下では、もう少し詳しい分岐図として次のような図を用いる。
（注意：以降の分岐図では、報酬関数$\ g \ $が現状態と行動だけでなく次状態にも依存するようになってしまっています、ごめんなさい。これは報酬関数の定義によって変わる問題であり、どちらで定式化しても同じ結論になります。）

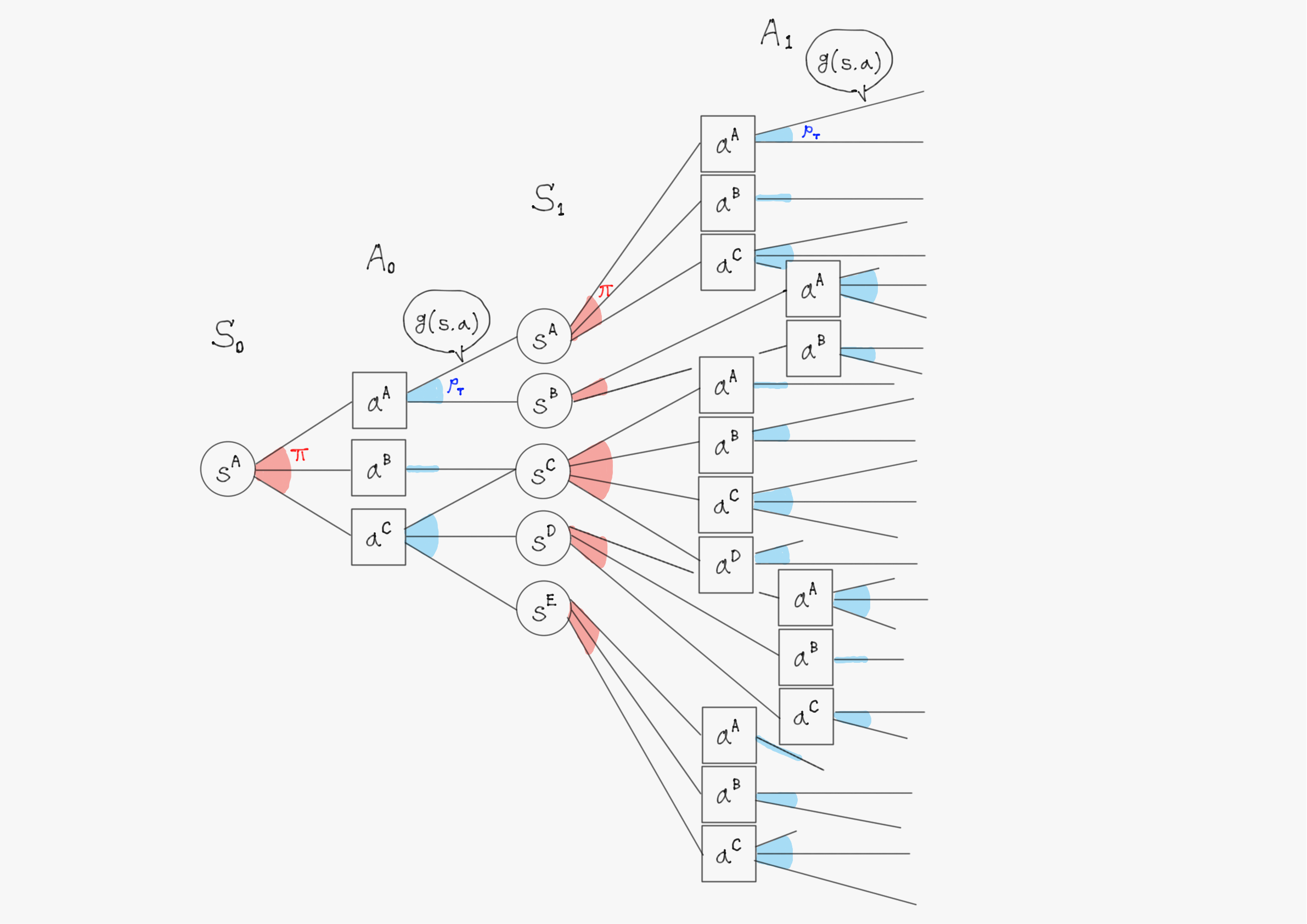
確率変数$\ S_t \ $や$\ A_t \ $の具体的な実現値として$\ s^A, s^B, \cdots \ $や$\ a^A, a^B, \cdots \ $といった値が入ると考えて欲しい。
扇形の色付きの部分は、その部分が確率的に選択される分岐であることを意味している。また、赤色は確率分布として方策$\pi$が、青色は状態遷移関数$\ p_T \ $が適用されることを意味している。

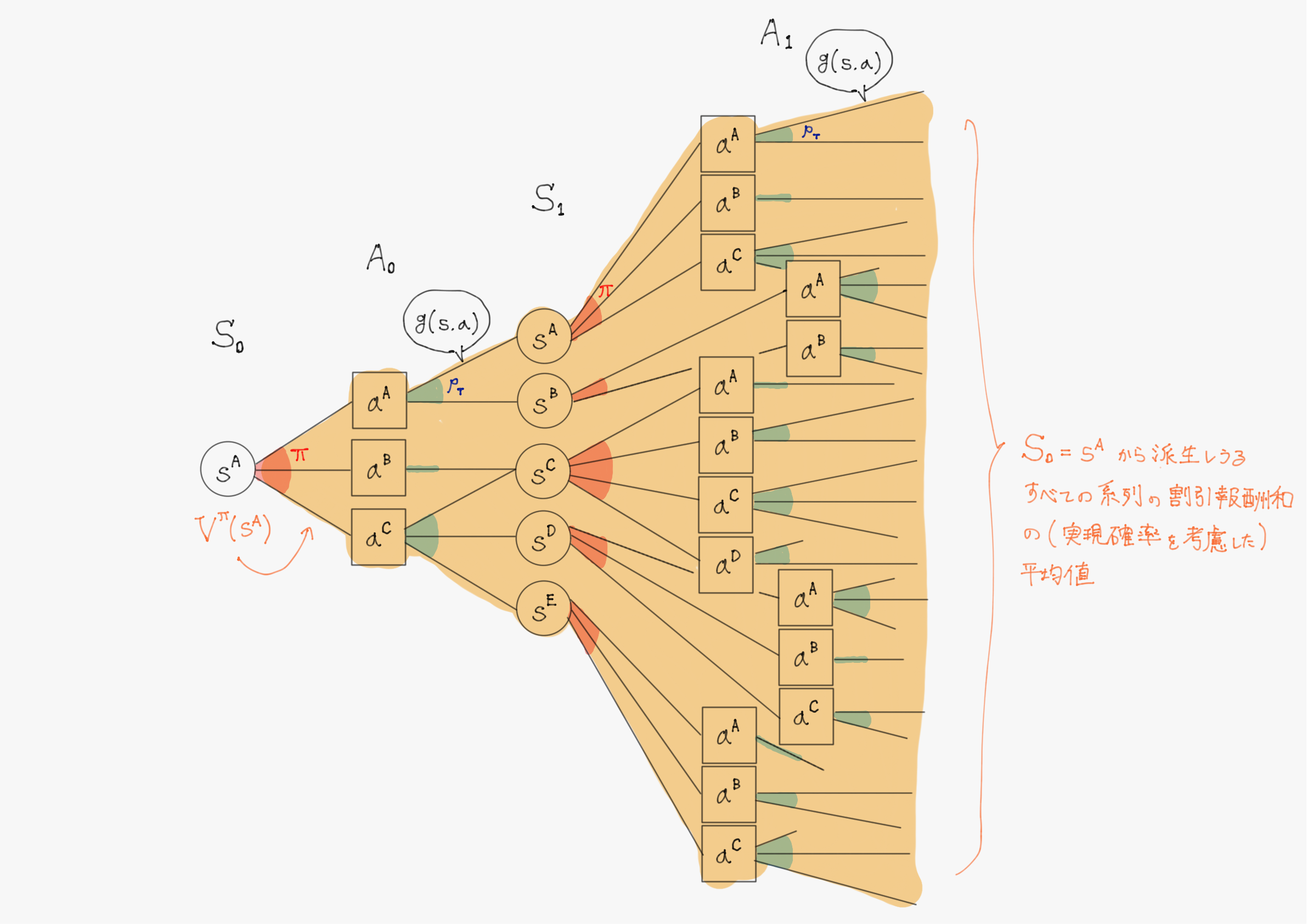
ここで、次のような二つの期待値を考える。

$V^{\pi}(s) \triangleq \underset{C_t \ \sim \ \Pr(C_t)}{\mathbb{E}} \left\lbrack C_t \mid S_t=s \right\rbrack$
→ 時刻$\ t \ $で状態$\ s \ $にいるとき、そこから方策$\ \pi \ $に従って行動を重ねていって得られるであろう割引報酬和$\ C_t \ $の期待値
→ 状態$\ s \ $の価値（良さ）と考えられる
→ $\ V^{\pi}(s) \ $を状態価値関数という

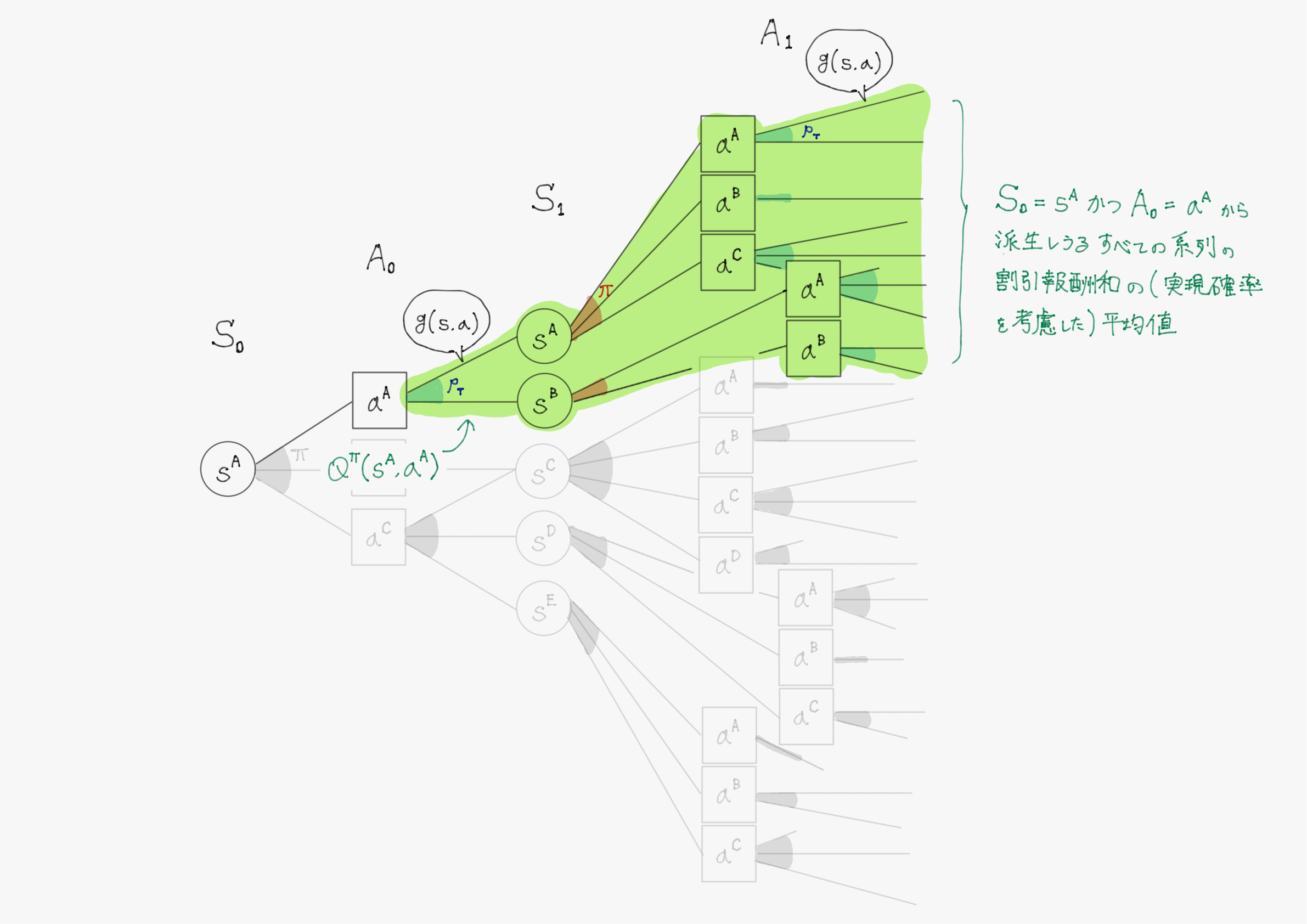
$Q^{\pi}(s,a) \triangleq \underset{C_t \ \sim \ \Pr(C_t)}{\mathbb{E}} \left\lbrack C_t \mid S_t=s, A_t=a \right\rbrack$
→ 時刻$\ t \ $で状態$\ s \ $にいてそこで行動$\ a \ $をとったとき、以降の行動は方策$\ \pi \ $に従うとするとして得られるであろう割引報酬和$\ C_t \ $の期待値
→ 状態$\ s \ $で行動$\ a \ $を選択することの価値（良さ）と考えられる
→ $Q^{\pi}(s,a)$を状態行動価値関数という

仮に、今いる状態$\ s \ $における$\ V^\pi(s) \ $や、そこで行動$\ a \ $取ったときの$\ Q^\pi(s,a) \ $が正確にわかったなら、$V^\pi(s), Q^\pi(s,a) \ $の値が高い状態へと遷移し続ける方策が最も良い方策である。
しかし前述の通り、 「正確に」求めるためにはエージェントが全ての系列を実際に生成する必要があり、これは膨大な時間がかかるため実質不可能である。
従って、推定値を少しずつ更新して正確にしていくが、これが**強化学習の「学習」**に相当する。

状態価値関数のもう少し詳しい図解

実際に上で使った図を用いて、もう少し詳しく状態価値関数の計算を説明することを試みる。

簡単のため、上の図で描写されていた$\ t=1 \ $までで計算を行い、割引率$\ \gamma=1 \ $として計算する。また、計算の仕組みを理解してもらうことが目的のため、確率（図中の赤色・青色で書かれた数字）や報酬（図中の吹き出しで囲まれた数値）の値は適当に設定していることに留意して欲しい。

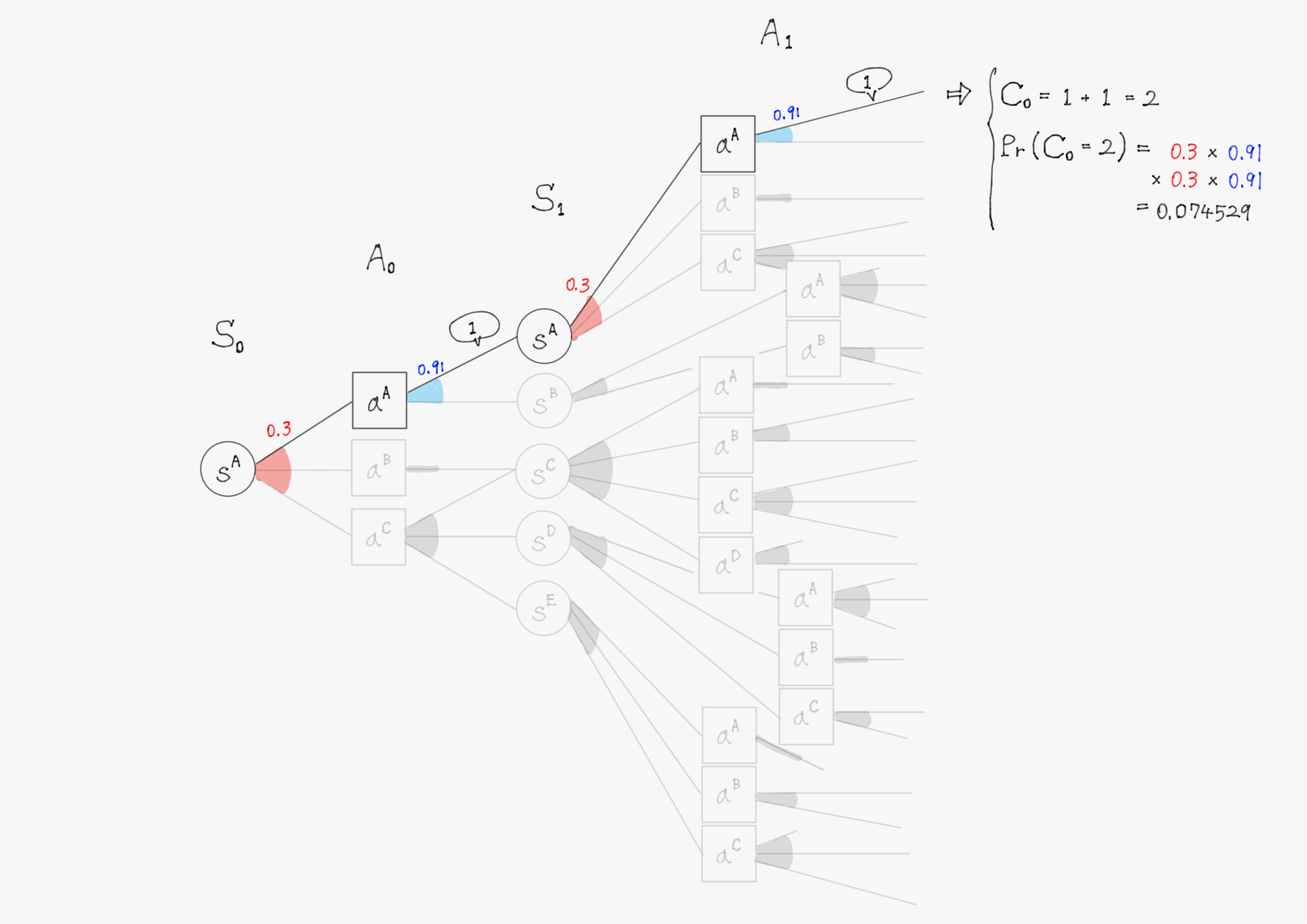
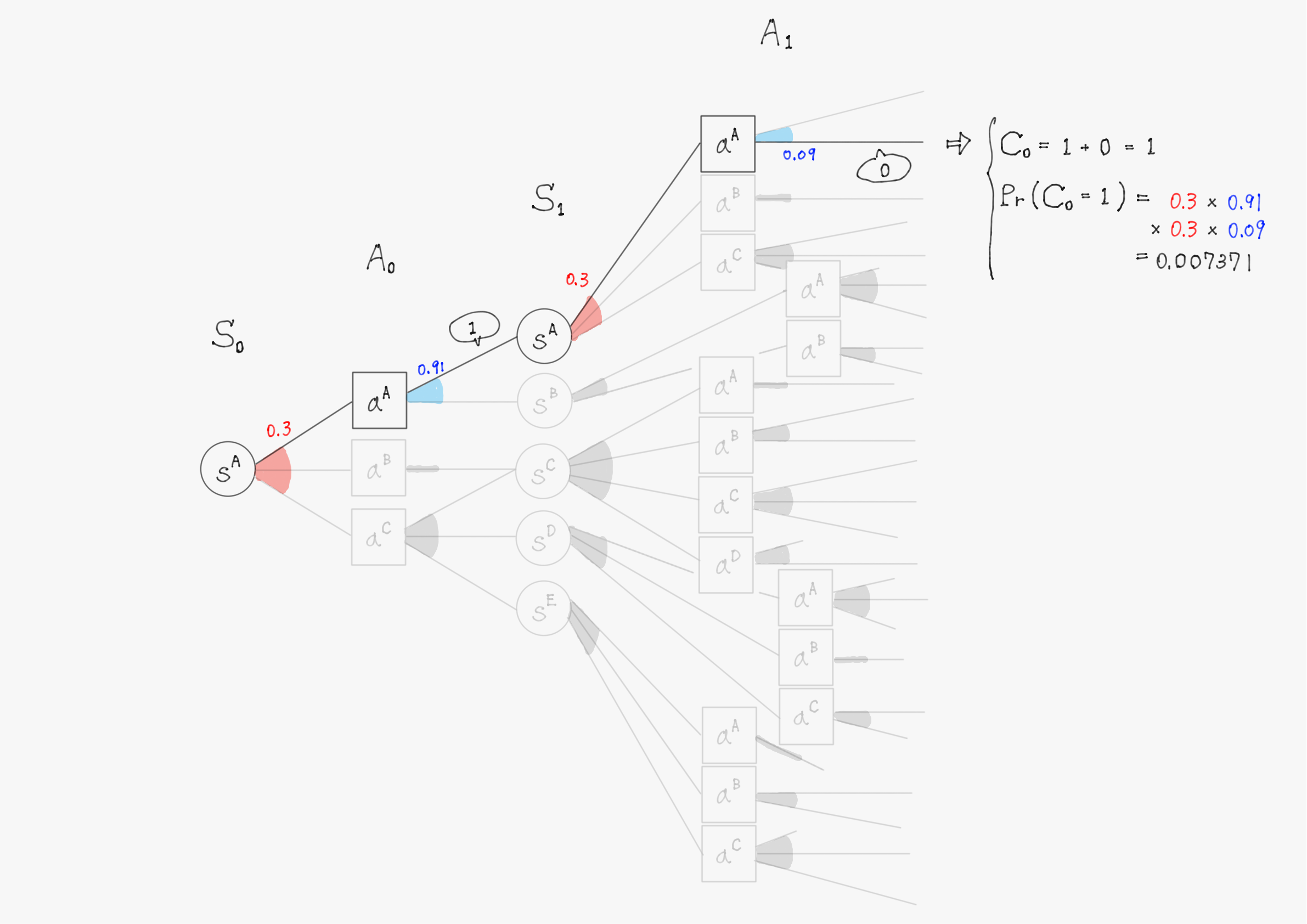
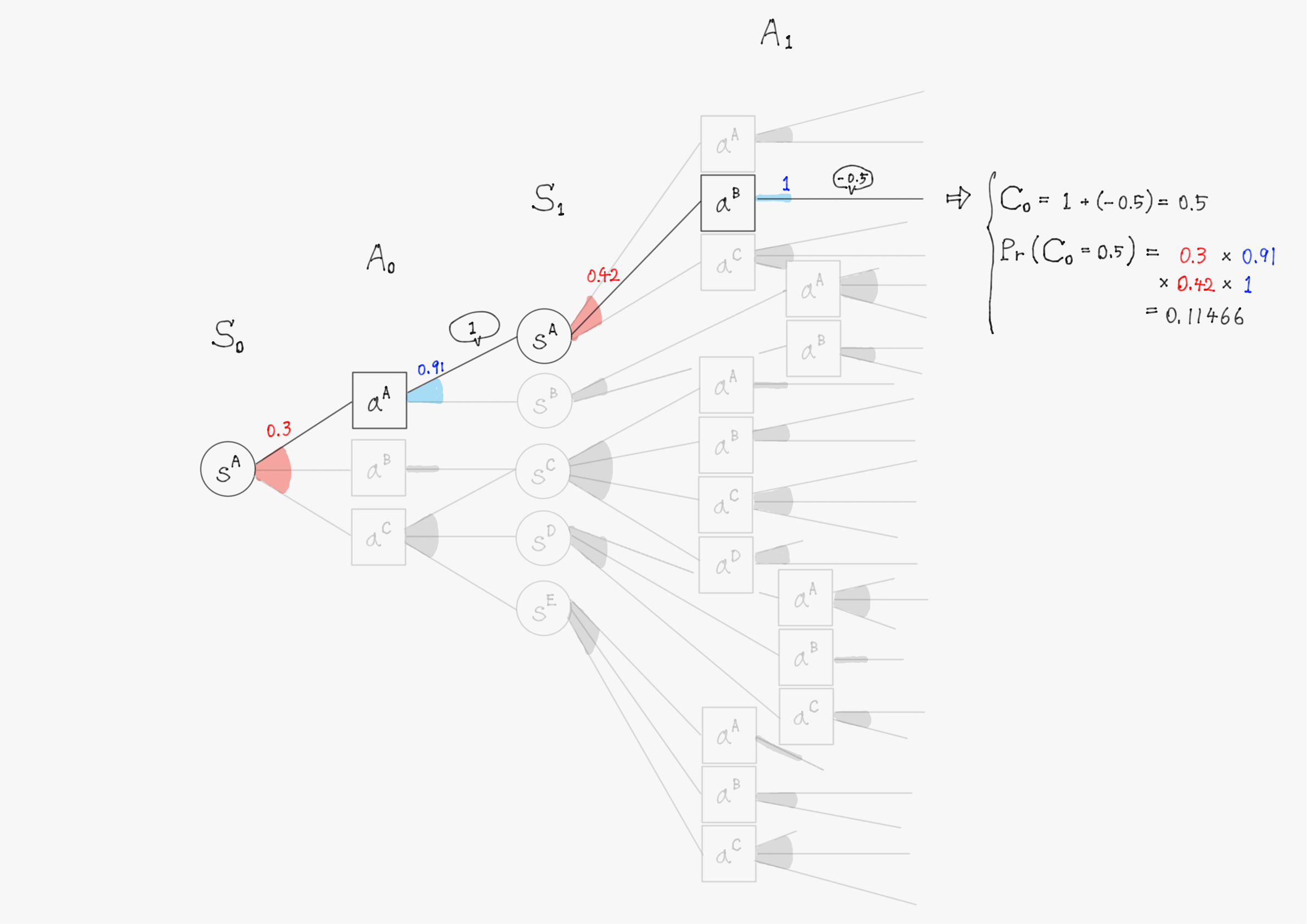
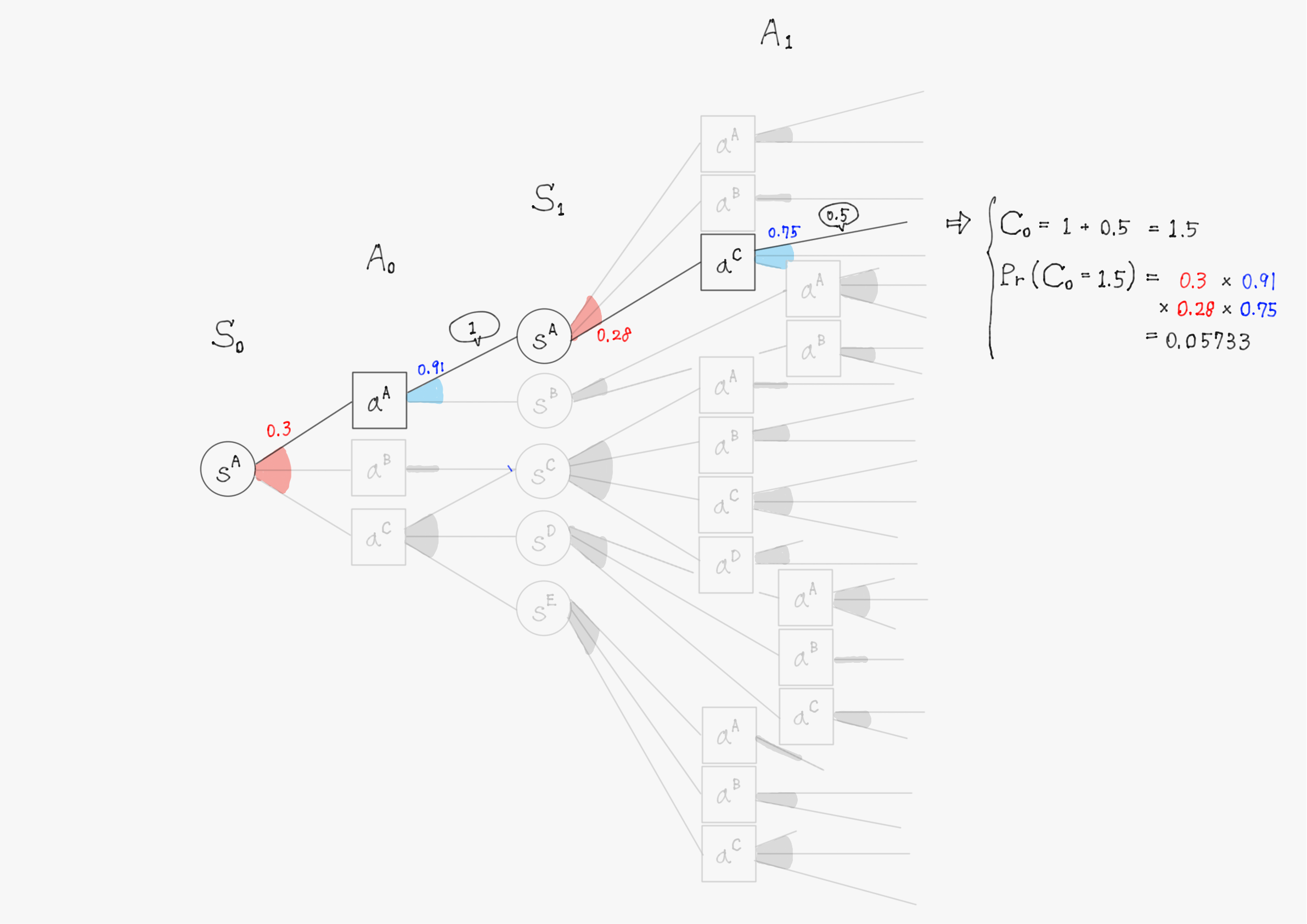
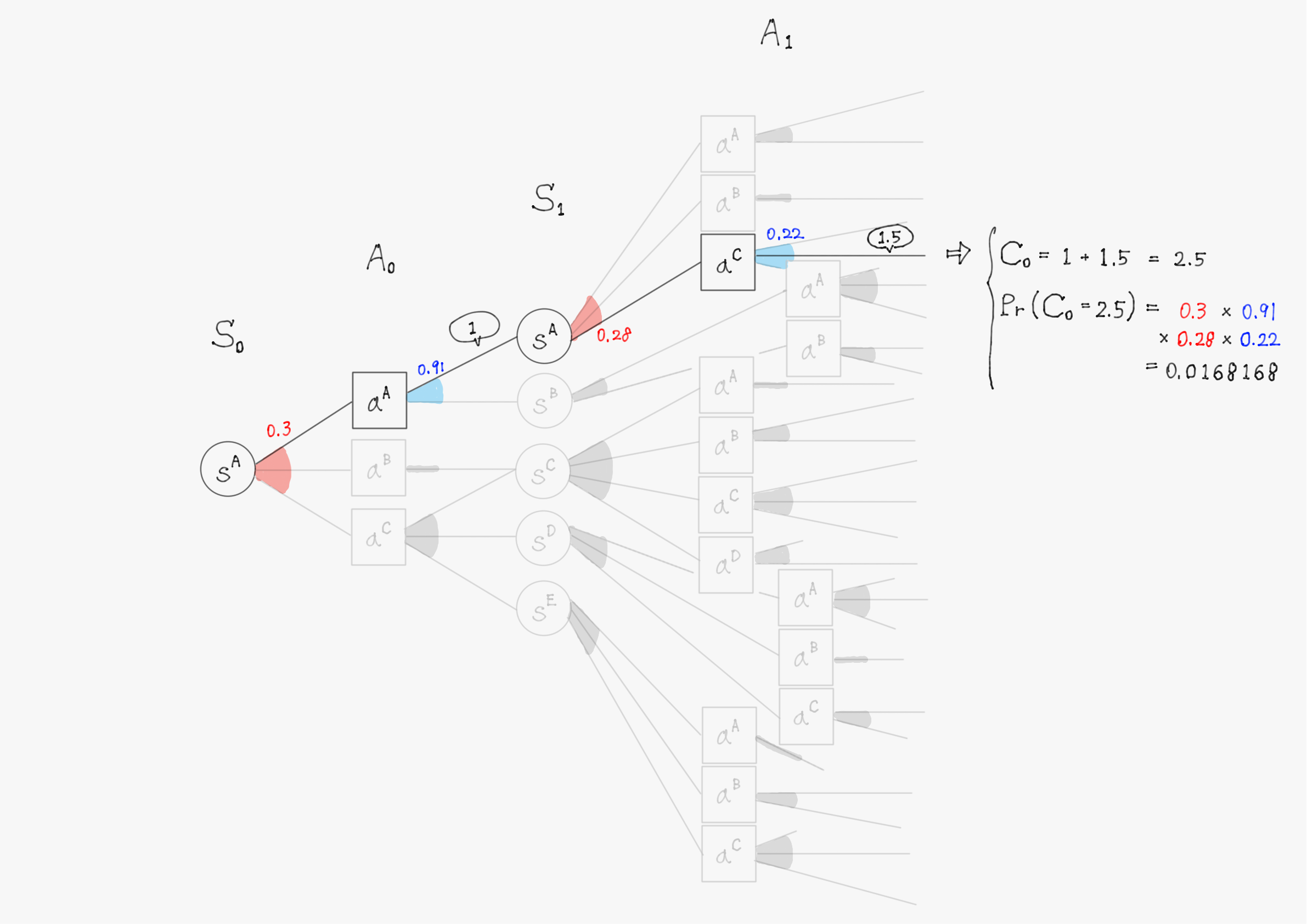
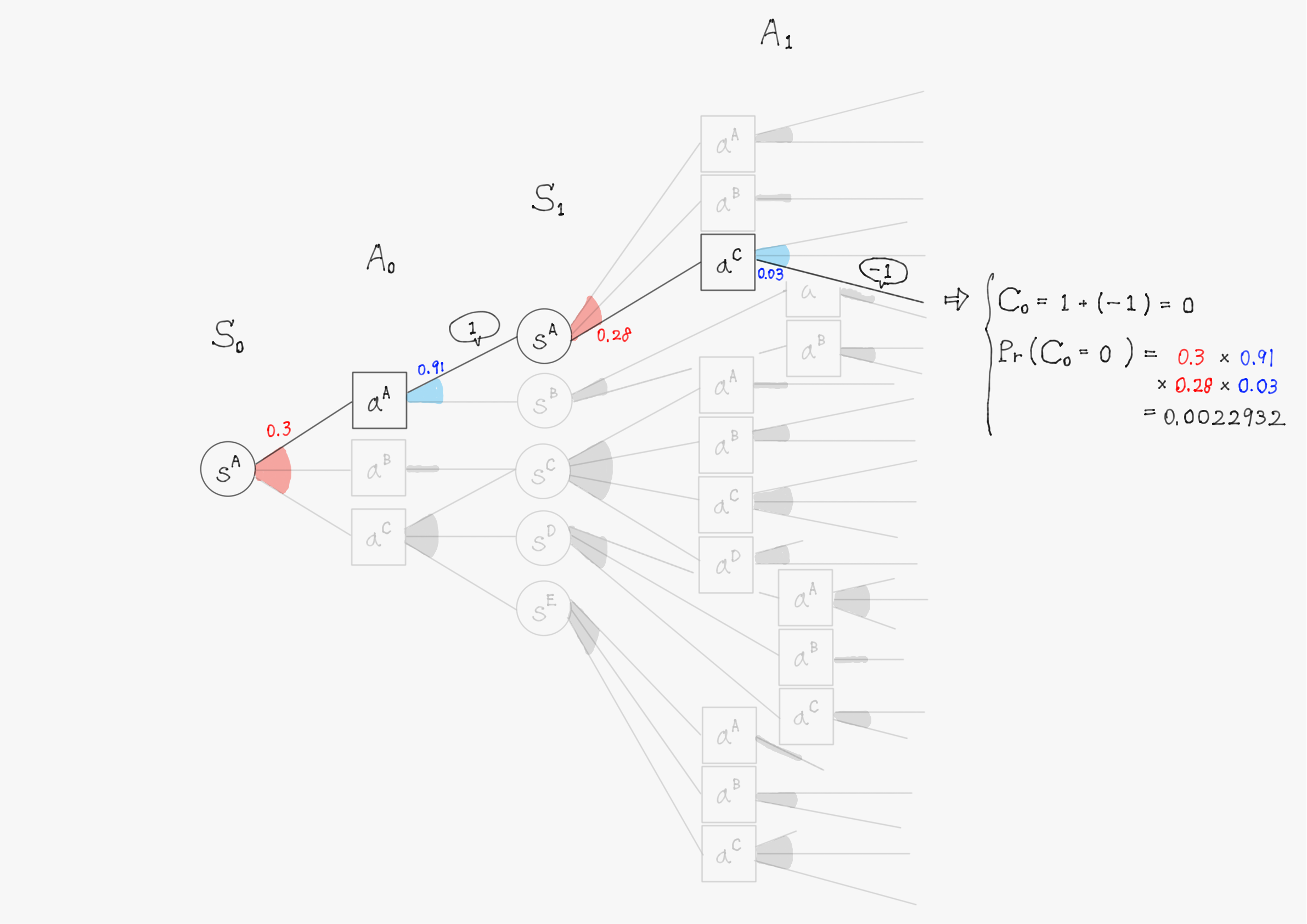
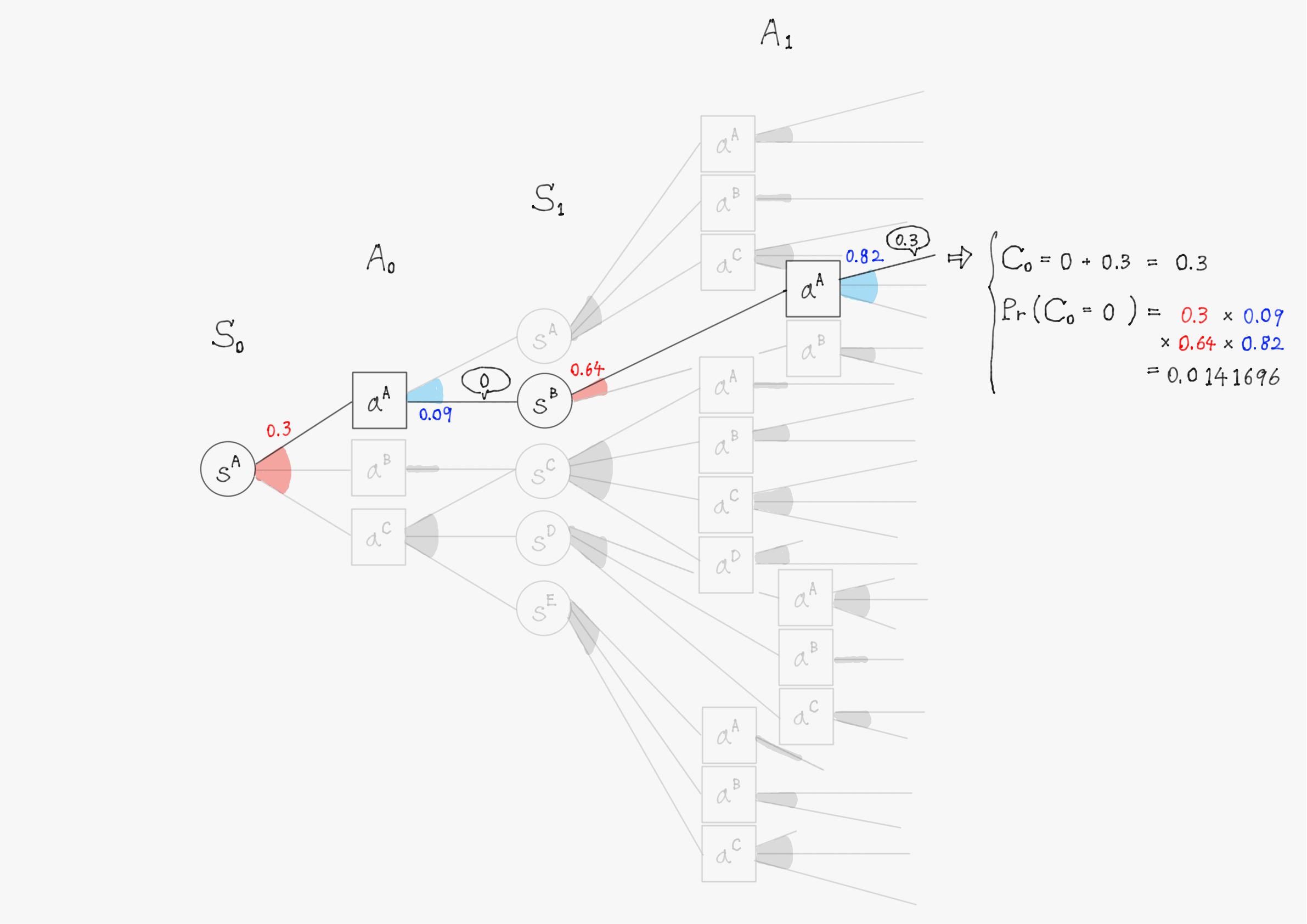
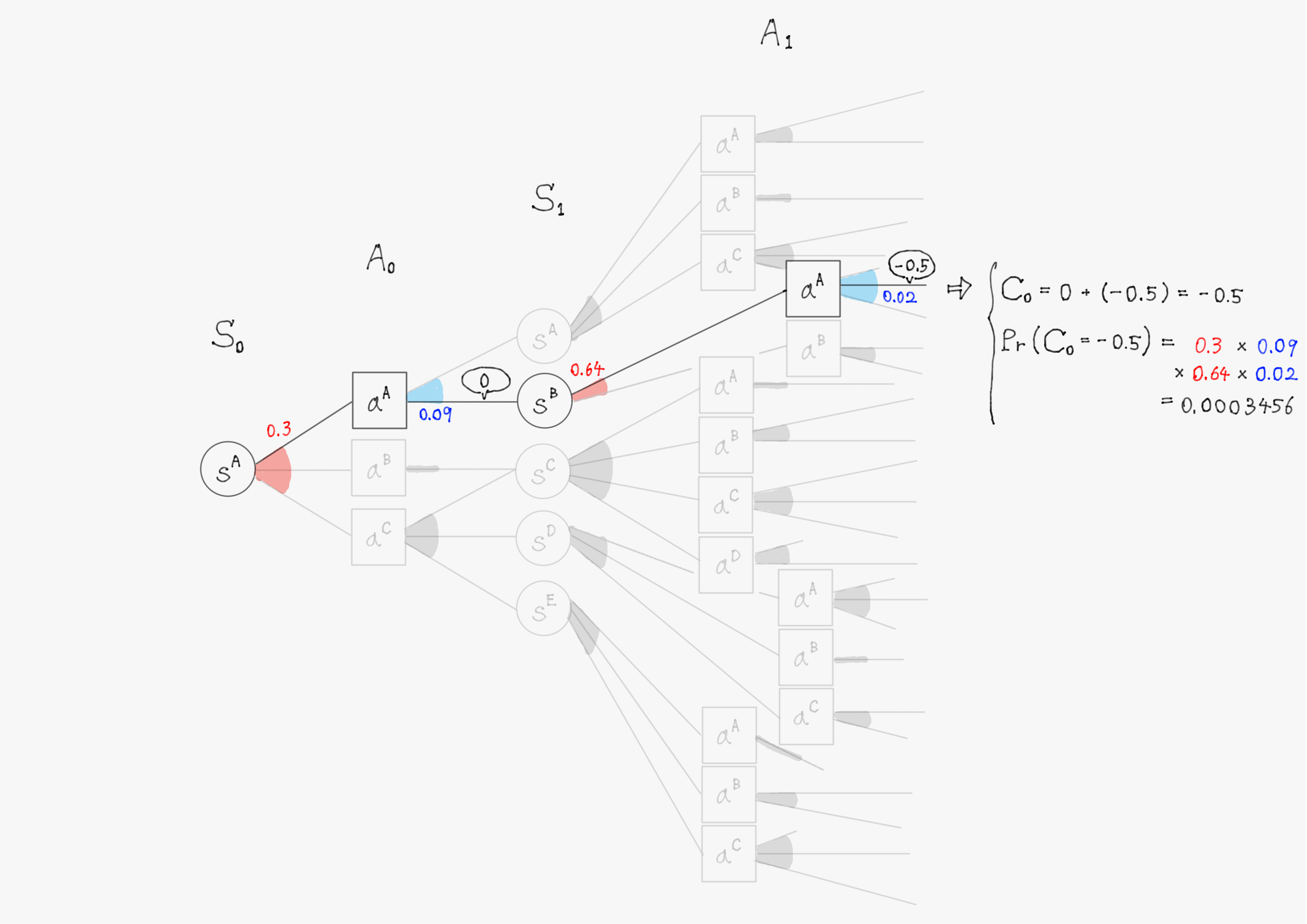
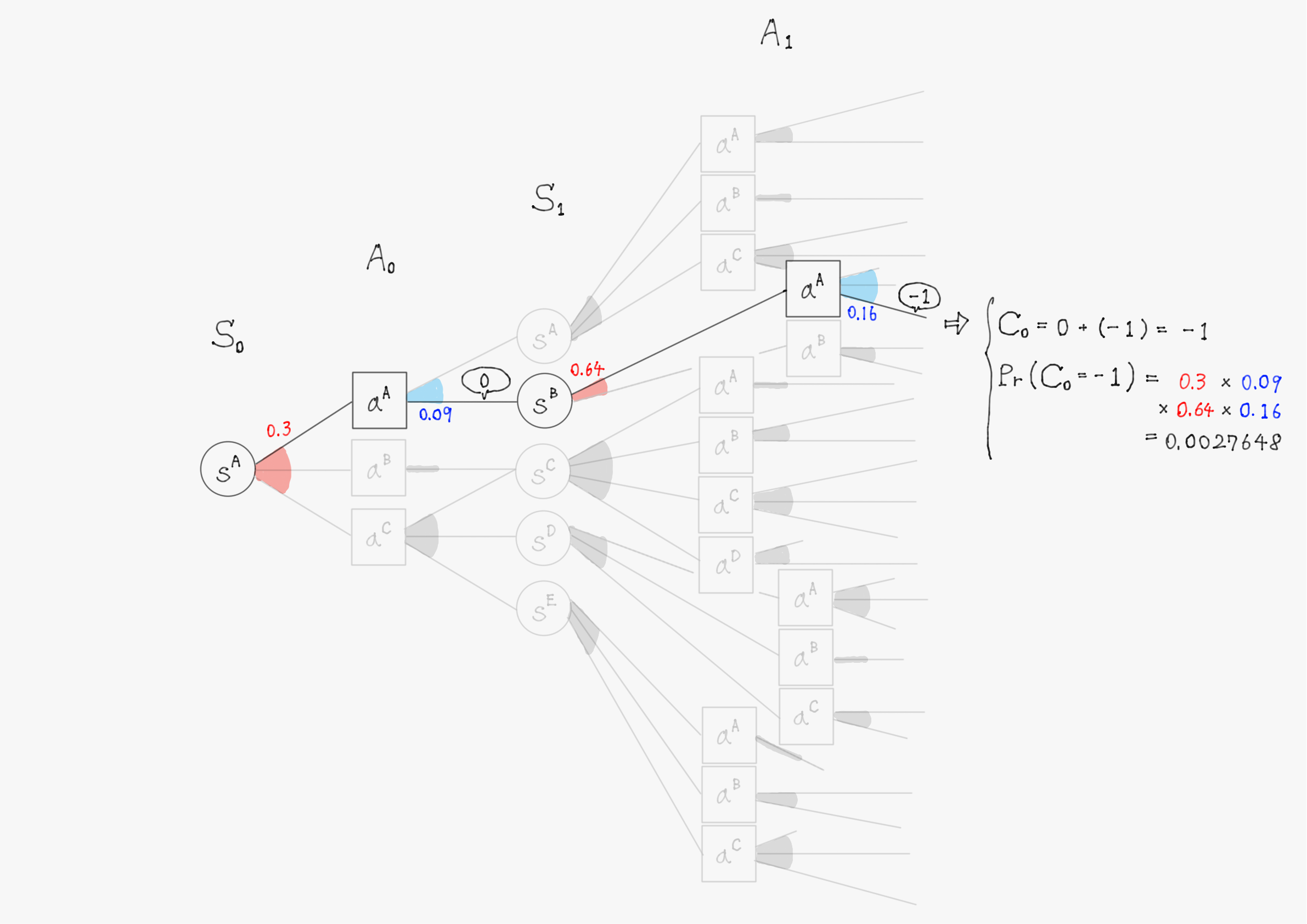
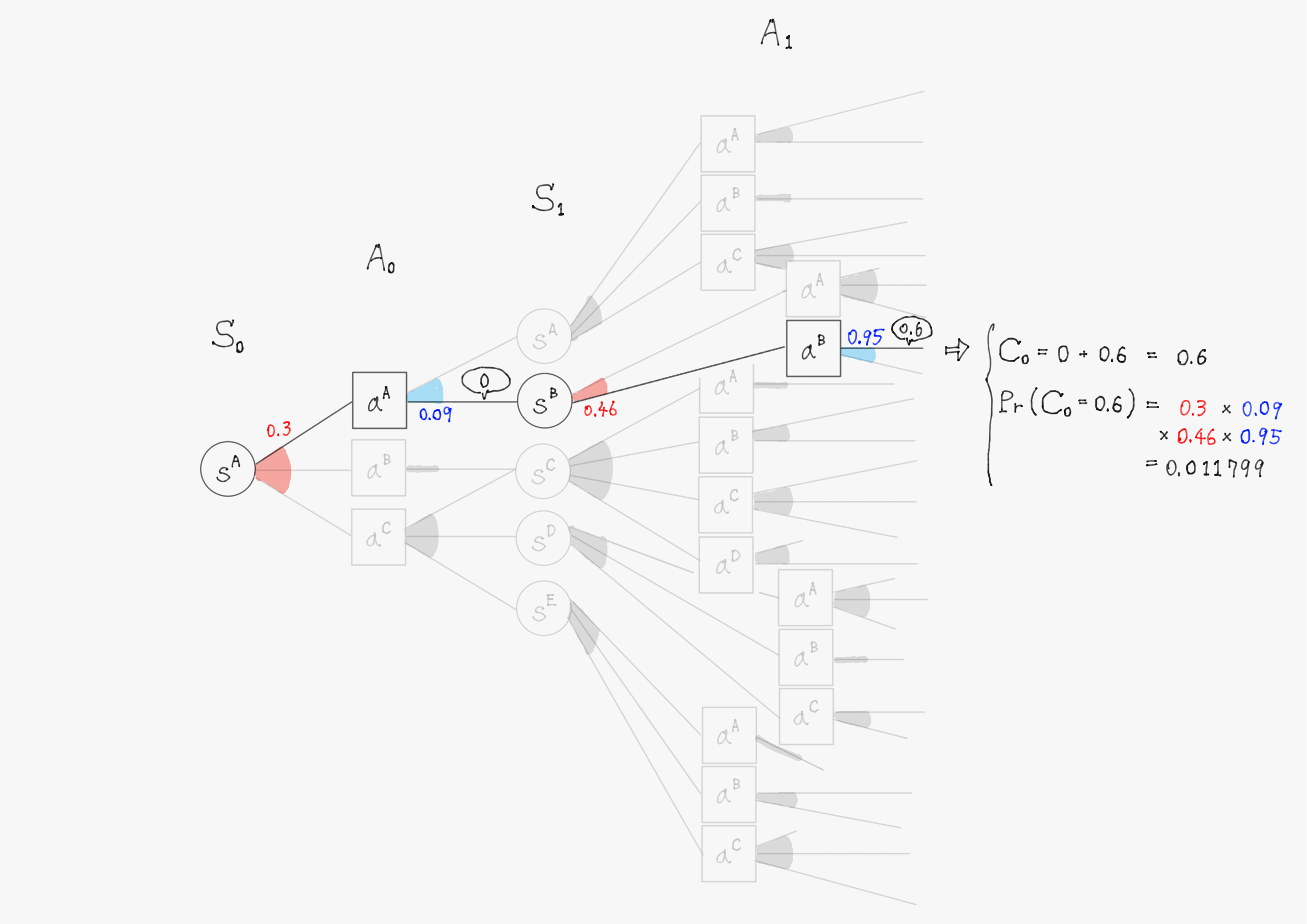
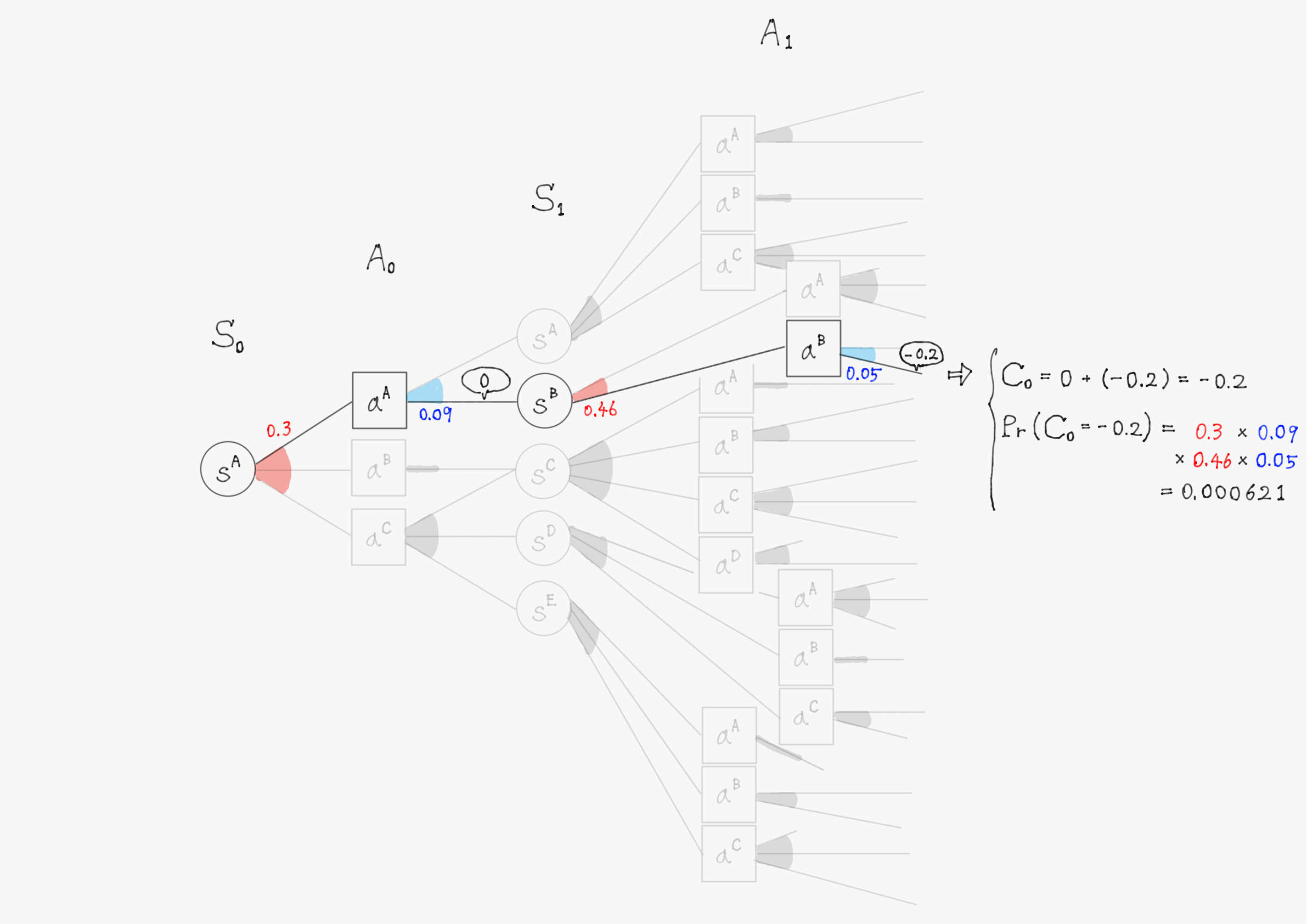
このようにして他の分岐についても計算を進めると、割引報酬和$\ C_0 \ $として以下のような31個（図の分岐の総数）の実現値が得られるはずである。

C_0 =
\begin{cases}
  2 & \bigl(\mathrm{Pr}(C_0=2)=0.074529 \bigr) \\
  1 & \bigl(\mathrm{Pr}(C_0=1)=0.007371 \bigr) \\
  0.5 & \bigl(\mathrm{Pr}(C_0=0.5)=0.11466 \bigr) \\
  1.5 & \bigl(\mathrm{Pr}(C_0=1.5)=0.05733 \bigr) \\
  2.5 & \bigl(\mathrm{Pr}(C_0=2.5)=0.0168168 \bigr) \\
  0 & \bigl(\mathrm{Pr}(C_0=0)=0.0022932 \bigr) \\
  0.3 & \bigl(\mathrm{Pr}(C_0=0.3)=0.0141696 \bigr) \\
  -0.5 & \bigl(\mathrm{Pr}(C_0=-0.5)=0.0003456 \bigr) \\
  -1 & \bigl(\mathrm{Pr}(C_0=-1)=0.0027648 \bigr) \\
  0.6 & \bigl(\mathrm{Pr}(C_0=0.6)=0.011799 \bigr) \\
  -0.2 & \bigl(\mathrm{Pr}(C_0=-0.2)=0.000621 \bigr) \\
  &\vdots
\end{cases}

あとは、定義通り期待値を計算すれば良い。

\begin{align}
  V^\pi(s^A)
  &=
  \underset{C_0 \ \sim \ \Pr(C_0)}{\mathbb{E}} \left\lbrack C_0 \mid S_0=s^A \right\rbrack \\
  &=
  2 \cdot 0.074529
  +
  1 \cdot 0.007371
  +
  0.5 \cdot 0.11466
  + \cdots
\end{align}

このように状態価値関数を厳密に計算するには実際に全ての分岐を辿る必要があるが、次節以降に説明するやり方でこれを近似的に求める。

2.2.6 Bermann方程式の導出

期待値の補題や式$(\diamondsuit)$を用いることで、状態価値関数$\ V^{\pi}(s) \ $と状態行動価値関数$\ Q^{\pi}(s,a) \ $をより更新のしやすい再帰的な形に書き換えることができる。

状態価値関数$V^\pi(s)$について

\begin{align}
  V^{\pi}(s)
  = {} &
  \underset{C_t \ \sim \ \Pr(C_t)}{\mathbb{E}}
  \left\lbrack
    C_t \mid S_t=s
  \right\rbrack \\
  = {} &
  \sum_{a \in \mathcal{A}} 
    \underset{C_t \ \sim \ \Pr(C_t)}{\mathbb{E}}
    \left\lbrack
      C_t \mid S_t=s, A_t=a
    \right\rbrack
    \cdot \mathrm{Pr}(A_t=a \mid S_t=s)
  \qquad
  (\because \text{期待値の補題}) \\
  = {} &
  \sum_{a \in \mathcal{A}} 
    \underset{C_t \ \sim \ \Pr(C_t)}{\mathbb{E}}
    \left\lbrack
      C_t \mid S_t=s, A_t=a
    \right\rbrack
    \cdot \pi(a \mid s) 
  \qquad
  (\because \text{方策$\pi$の定義}) \\
  = {} &
  \sum_{a \in \mathcal{A}}
    \pi(a \mid s)
    \cdot  
    \underset{C_t \ \sim \ \Pr(C_t)}{\mathbb{E}}
    \left\lbrack
      C_t \mid S_t=s, A_t=a
    \right\rbrack \\
  = {} &
  \sum_{a \in \mathcal{A}}
    \pi(a \mid s)
    \cdot
    \sum_{s' \in \mathcal{S}}
      \underset{C_t \ \sim \ \Pr(C_t)}{\mathbb{E}}
      \left\lbrack
        C_t \mid S_t=s, A_t=a, S_{t+1}=s'
      \right\rbrack
      \cdot
      \mathrm{Pr}(S_{t+1}=s' \mid S_t=s, A_t=a)
  \qquad
  (\because \text{期待値の補題}) \\
  = {} &
  \sum_{a \in \mathcal{A}}
    \pi(a \mid s)
    \cdot
    \sum_{s' \in \mathcal{S}}
      \underset{C_t \ \sim \ \Pr(C_t)}{\mathbb{E}}
      \left\lbrack
        C_t \mid S_t=s, A_t=a, S_{t+1}=s'
      \right\rbrack
      \cdot
      p_{\mathrm{T}}(s' \mid s,a)
  \qquad
  (\because \text{状態遷移確率$p_{\mathrm{T}}$の定義}) \\
  = {} &
  \sum_{a \in \mathcal{A}}
    \pi(a \mid s)
    \cdot
    \sum_{s' \in \mathcal{S}}
      p_{\mathrm{T}}(s' \mid s,a)
      \cdot
      \underset{C_t \ \sim \ \Pr(C_t)}{\mathbb{E}}
      \left\lbrack
        C_t \mid S_t=s, A_t=a, S_{t+1}=s'
      \right\rbrack \\
  = {} &
  \sum_{a \in \mathcal{A}}
    \pi(a \mid s)
    \cdot
    \sum_{s' \in \mathcal{S}}
      p_{\mathrm{T}}(s' \mid s,a)
      \cdot
      \underset{C_t \ \sim \ \Pr(C_t)}{\mathbb{E}}
      \left\lbrack
        R_t + \gamma C_{t+1} \mid S_t=s, A_t=a, S_{t+1}=s'
      \right\rbrack
  \qquad
  (\because \text{式}(\diamondsuit)) \\
  = {} &
  \sum_{a \in \mathcal{A}}
    \pi(a \mid s)
    \cdot
    \sum_{s' \in \mathcal{S}}
      p_{\mathrm{T}}(s' \mid s,a)
      \cdot \\
      & \qquad
      \left(
        \underset{R_t \ \sim \ \Pr(R_t)}{\mathbb{E}}
        \left\lbrack
          R_t \mid S_t=s, A_t=a, S_{t+1}=s'　
        \right\rbrack
        +
        \underset{C_{t+1} \ \sim \ \Pr(C_{t+1})}{\mathbb{E}}
        \left\lbrack
          \gamma C_{t+1} \mid S_t=s, A_t=a, S_{t+1}=s'
        \right\rbrack
      \right)
  \qquad -(\clubsuit)
\end{align}

ここで、状態$\ s \ $とそこでとった行動$\ a \ $が与えられている場合、報酬関数$\ g(s,a) \ $より環境から受け取る報酬は一意に定まるので、式$(\clubsuit)$の括弧内第1項に関しては

\underset{R_t \ \sim \ \Pr(R_t)}{\mathbb{E}}
\left\lbrack
  R_t \mid S_t=s, A_t=a, S_{t+1}=s'　
\right\rbrack
=
g(s,a) \qquad -(1)

が成り立つ。

また、マルコフ性（現在の状態$\ S_t \ $が直前の状態$\ S_{t-1} \ $にのみ依存する）という性質を仮定すると、下記の手順で依存関係を見ていくことで式$(\clubsuit)$の括弧内第2項の割引報酬和$\ C_{t+1}$の期待値も$S_t, A_t \ $に依存せず定まることがわかる。

1. $\ C_{t+1} \ $は$\ R_{t+k} \ ( k \geq 1 ) \ $に依存（参考：割引報酬和の定義式$\ C_t \triangleq \sum_{k=0}^{K-1} \gamma^k R_{t+k} \ $）
2. $\ R_{t+k} \ $は報酬$\ r \ $の確率変数であり、これは状態$\ S_{t+k} \ $と行動$\ A_{t+k} \ $によって報酬関数$\ g(s,a) \ $から一意に定まる
3. よって$\ C_{t+1} \ $が依存している状態変数の中で時間的に最も昔のものは、$k=1 \ $の時の$\ S_{t+1} \ $だが、これは期待値の条件として$\ S_{t+1} = s'$と与えられているためすでに変数ではなく、$\ C_{t+1} \ $は$\ S_{t+2} \ $以降の状態変数に依存する
4. $\ S_{t+2} \ $がどの値を取るかはマルコフ性から$\ S_{t+1} \ $にのみ依存し、それ以前の変数には依存しない

よって、

\begin{align}
\underset{C_{t+1} \ \sim \ \Pr(C_{t+1})}{\mathbb{E}}
\left\lbrack
  \gamma C_{t+1} \mid S_t=s, A_t=a, S_{t+1}=s'
\right\rbrack
=
\underset{C_{t+1} \ \sim \ \Pr(C_{t+1})}{\mathbb{E}}
\left\lbrack
  \gamma C_{t+1} \mid S_{t+1}=s'
\right\rbrack \qquad -(2)
\end{align}

も成り立つ。

式$\ (1),(2) \ $より、式$\ (\clubsuit) \ $は次のように変形できる。

\begin{align}
  (\clubsuit)
  = {} &
  \sum_{a \in \mathcal{A}}
    \pi(a \mid s)
    \cdot
    \sum_{s' \in \mathcal{S}}
      p_{\mathrm{T}}(s' \mid s,a)
      \cdot
      \left(
        g(s,a)
        +
        \underset{C_{t+1} \ \sim \ \Pr(C_{t+1})}{\mathbb{E}}
        \left\lbrack
          \gamma C_{t+1} \mid S_{t+1}=s'
        \right\rbrack
      \right)
  &
  (\because \text{式(1),(2)}) \\
  = {} &
  \sum_{a \in \mathcal{A}}
    \pi(a \mid s)
    \cdot
    \sum_{s' \in \mathcal{S}}
    \Bigl(
      p_{\mathrm{T}}(s' \mid s,a)
      \cdot
      g(s,a)
      +
      p_{\mathrm{T}}(s' \mid s,a)
      \cdot
      \gamma 
      V^{\pi}(s')
    \Bigr)
  &
  (\because \text{状態価値関数$V^{\pi}(s)$の定義})\\
  = {} &
  \sum_{a \in \mathcal{A}}
    \pi(a \mid s)
    \cdot
    \left(
    g(s,a)
    \sum_{s' \in \mathcal{S}}
      p_{\mathrm{T}}(s' \mid s,a)        
    +
    \gamma
    \sum_{s' \in \mathcal{S}}
      p_{\mathrm{T}}(s' \mid s,a)
      \cdot
      V^{\pi}(s')
    \right) \\
  = {} &
  \sum_{a \in \mathcal{A}}
    \pi(a \mid s)
    \cdot
    \left(
    g(s,a)  
    +
    \gamma
    \sum_{s' \in \mathcal{S}}
      p_{\mathrm{T}}(s' \mid s,a)
      \cdot
      V^{\pi}(s')
    \right)
  &
  (\because \text{確率の和は$1$})
\end{align}

まとめると、以下のような式が成り立つ。

V^{\pi}(s)
=
\sum_{a \in \mathcal{A}}
  \pi(a \mid s)
  \cdot
  \left(
  g(s,a)  
  +
  \gamma
  \sum_{s' \in \mathcal{S}}
    p_{\mathrm{T}}(s' \mid s,a)
    \cdot
    V^{\pi}(s')
  \right)

この式はBermann方程式と呼ばれ、各種強化学習の基礎となる重要な式である。

式の説明をすると、現在の状態における価値$\ V^{\pi}(s) \ $とは、

1. 現状態から遷移しうる全ての可能性$\ p_{\mathrm{T}}(s' \mid s,a) \ $について1つ先の状態での価値$\ V^{\pi}(s') \ $を平均した値と
2. 現在の状態から1つ先の状態に遷移する際に得られる報酬$\ g(s,a) \ $を足し合わせ、
3. さらにそれぞれの行動を選択する可能性$\ \pi(a \mid s) \ $を考慮して平均を取った値

であるという意味。（前述の分岐図を見るとよりわかりやすい。）
この式を用いれば、前節の「状態価値関数のもう少し詳しい図解」で確認したように全ての分岐を実際に体験しなくては計算できなかった状態価値$\ V^{\pi}(s) \ $の近似値を、エージェントが繰り返し環境と相互作用することで計算できるようになる。なぜなら、式が再帰構造（現在の状態価値$\ V^{\pi}(s) \ $が一つ先の状態価値$\ V^{\pi}(s') \ $を用いて計算できる）をしているため、とりあえず適当な値で初期化しておき、環境に対して行動して報酬$\ g(s,a) \ $が得られたらその都度式を使って微調整していくことができるからである。

状態行動価値関数$Q^\pi(s,a)$について

状態行動価値関数$Q^\pi(s,a)$は定義より

V^\pi(s)
=
\sum_a \pi(a \mid s)
  \cdot
  Q^\pi(s,a)

であるので、Bermann方程式に代入して計算すれば、

Q^\pi(s,a)
=
g(s,a) + \gamma
\sum_{s'} \sum_{a'} 
  \pi(a \mid s)
  \cdot
  p_{\mathrm{T}}(s' \mid s,a)
  \cdot
  Q^\pi(s',a')

第2回はこちら

参考文献

• 森村哲郎， 強化学習， 機械学習プロフェッショナルシリーズ， 講談社， 2019．
• 【強化学習】Bellman方程式の導入