0. はじめに
第1回では、強化学習の理論的背景を図と数式を交えて解説しました。
第2回の本記事では、古典的な強化学習の一つであるQ学習について解説し、実際にpythonを用いて迷路踏破Agentを実装します。
コードもこちらに公開しています。
なお本記事は、強化学習 Advent Calendar 2021の21日の記事です。
1. Q学習の理論
- 第1回で導出した状態行動価値関数$\ Q^\pi(s,a) \ $を学習する手法の一つ
- 次の状態$\ s' \ $で行動$\ a' \ $を取ったときの状態行動価値関数$\ \hat{Q}(s',a') \ $の値を$\ \max \ $で近似する
- 急激に変化させると学習が安定しないことがあるので、学習率$\ \alpha \ $で内分
1.1 大まかな手順
状態行動価値$\ Q^\pi(s,a) \ $は各状態$\ s \ $で行動$\ a \ $を取ったときの価値のようなものだった。
Q学習では、これを第1回の最後で導いたBellman方程式(少し書き換えている)
Q^\pi(s,a)
=
g(s,a) + \gamma
\sum_{s'}
p_{\mathrm{T}}(s' \mid s,a)
\cdot
\sum_{a'}
\pi(a’ \mid s')
\cdot
Q^\pi(s',a')
\qquad
-(\spadesuit)
を近似的に用いて更新していく手法である。
大まかな手順は以下の通り。手順③の更新式で具体的にどのような近似をしているかを早く知りたい人は、「1.4 Q学習の更新」まで飛ぶと良い。
- 手順①
- 全ての$\ (s,a) \ $の組について、状態行動価値の推定値$\ \hat{Q}(s,a) \ $を初期化(0で初期化するのが普通)
- 手順②
- エージェントは時刻$\ t \ $で状態$\ s_t \ $にいるとき、その時点での推定値$\ \hat{Q}(s_t,a_t) \ $に基づいて以下のように行動を選択する
- [活用] 確率$\ 1-\epsilon \ $で、$\underset{b \in \mathcal{A}}{\max}\hat{Q}(s_t,b) \ $となる行動$\ a \ $($\ a=\underset{b \in \mathcal{A}}{\mathrm{argmax}}\hat{Q}(s_t, b) \ $と書く)を選択
- [探索] 確率$\ \epsilon \ $で、ランダムに行動$\ a \ $を選択
- 手順③
- 行動選択によって環境から報酬$\ r_t=g(s_t,a_t) \ $が得られるので、式$\ (\spadesuit) \ $を近似した次式を使って状態行動価値の推定値$\ \hat{Q}(s_t,a_t) \ $を更新
$ \qquad \qquad \qquad \qquad \hat{Q}(s_t,a_t) \approx r_t + \gamma \underset{b \in \mathcal{A}}{\max} \hat{Q}(s_{t+1},b) \ $ - 手順④
- 手順②〜③を$\ \hat{Q}(s,a) \ $が収束するまで繰り返す
1.2 迷路探索の場合
前回の講義資料で定式化した迷路を使ってQ学習のイメージを説明する。
おさらいのためにこの迷路の数学的定式化を図にまとめた物を付しておく。
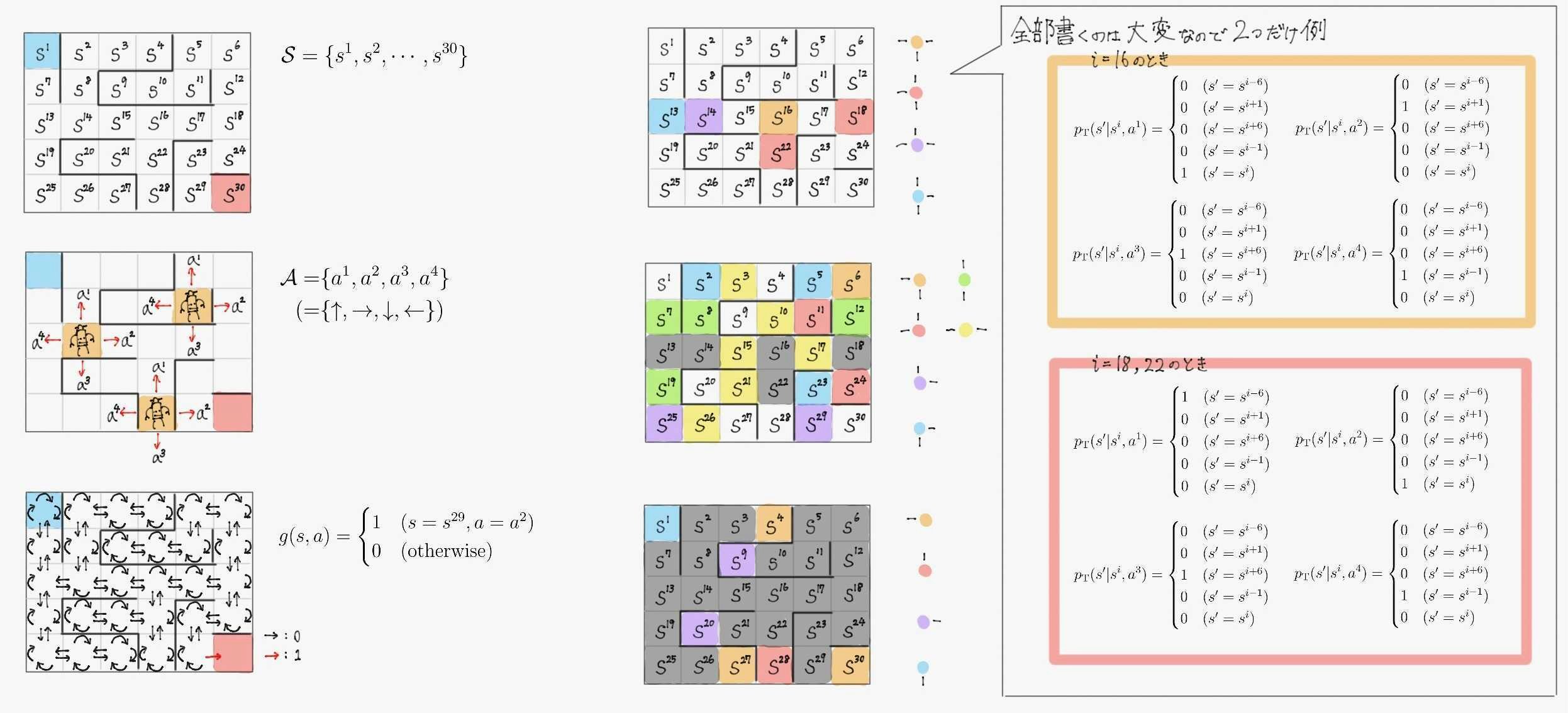
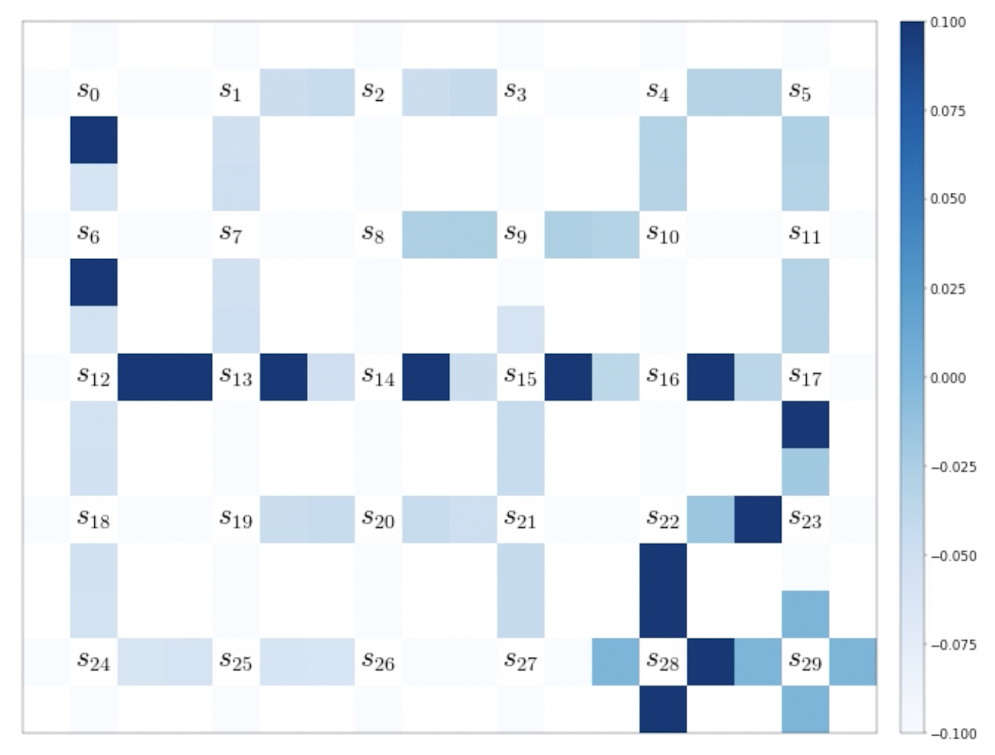
状態行動価値$\ \hat{Q}(s,a) \ $は各状態$\ s \ $の各行動$\ a \ $ごとに値が定められていることを考えると、下図のように迷路の1マスごとに上下左右の状態行動価値が割り当てられていると考えられる。
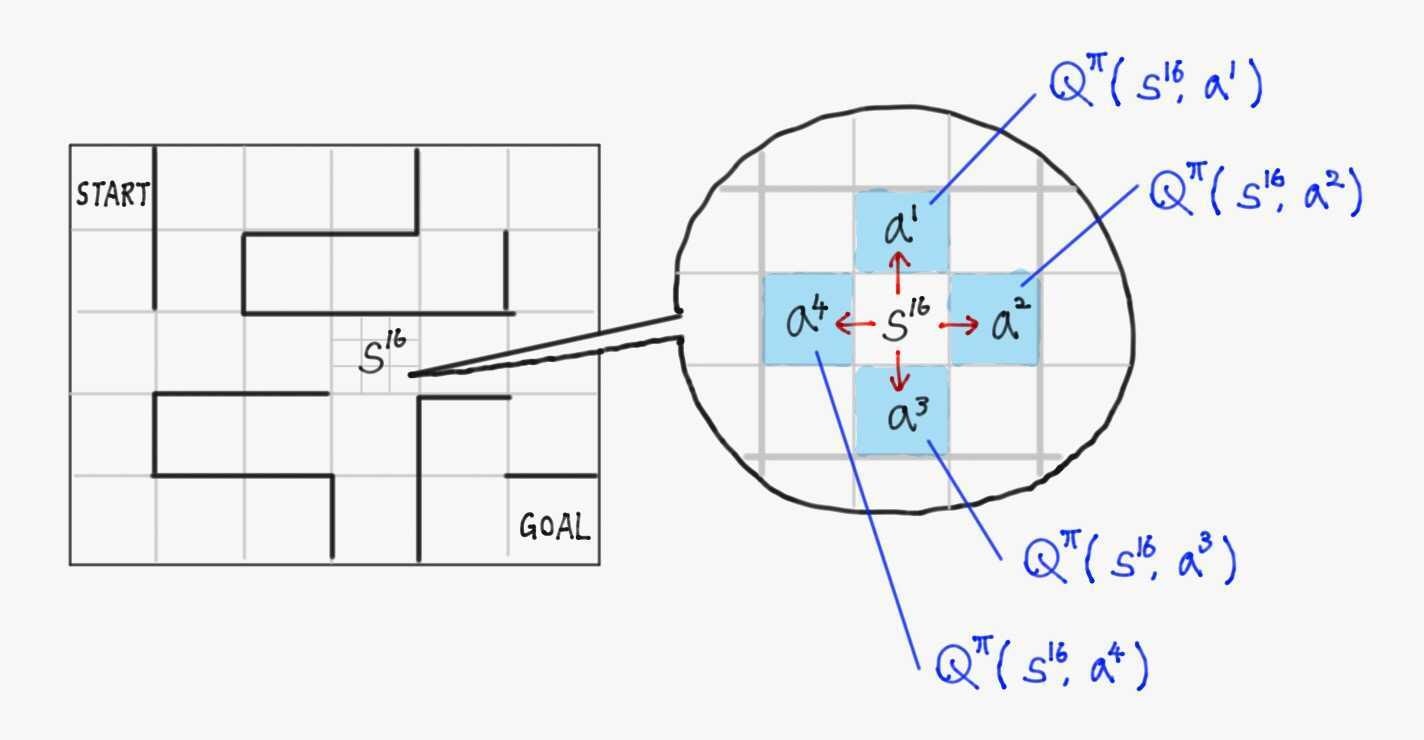
エージェントの目的は、この各マスに4つずつ割り当てられた価値を、「スタートから各マスでこの値が最大の値を取れば最短でゴールにつけるような値」にすること。
これは、第1回の「2.2.5 価値関数」の言葉を引用すれば、
$Q^{\pi}(s,a) \triangleq \underset{C_t \ \sim \ \Pr(C_t)}{\mathbb{E}} \left\lbrack C_t \mid S_t=s, A_t=a \right\rbrack$
→ 時刻$\ t \ $で状態$\ s \ $にいてそこで行動$\ a \ $をとったとき、以降の行動は方策$\ \pi \ $に従うとするとして得られるであろう割引報酬和$\ C_t \ $の期待値
→ **状態$\ s \ $で行動$\ a \ $を選択することの価値(良さ)**と考えられる(中略)
仮に、今いる状態$\ s \ $における$\ V^\pi(s) \ $や、そこで行動$\ a \ $取ったときの$\ Q^\pi(s,a) \ $が正確にわかったなら、$V^\pi(s), Q^\pi(s,a) \ $の値が高い状態へと遷移し続ける方策が最も良い方策である。
だからである。
このとき、前述の手順に従って行動すると、
- 手順①
- $0 \ $で全ての状態行動価値の推定値$\ \hat{Q}(s,a) \ $を初期化する。
- 手順②
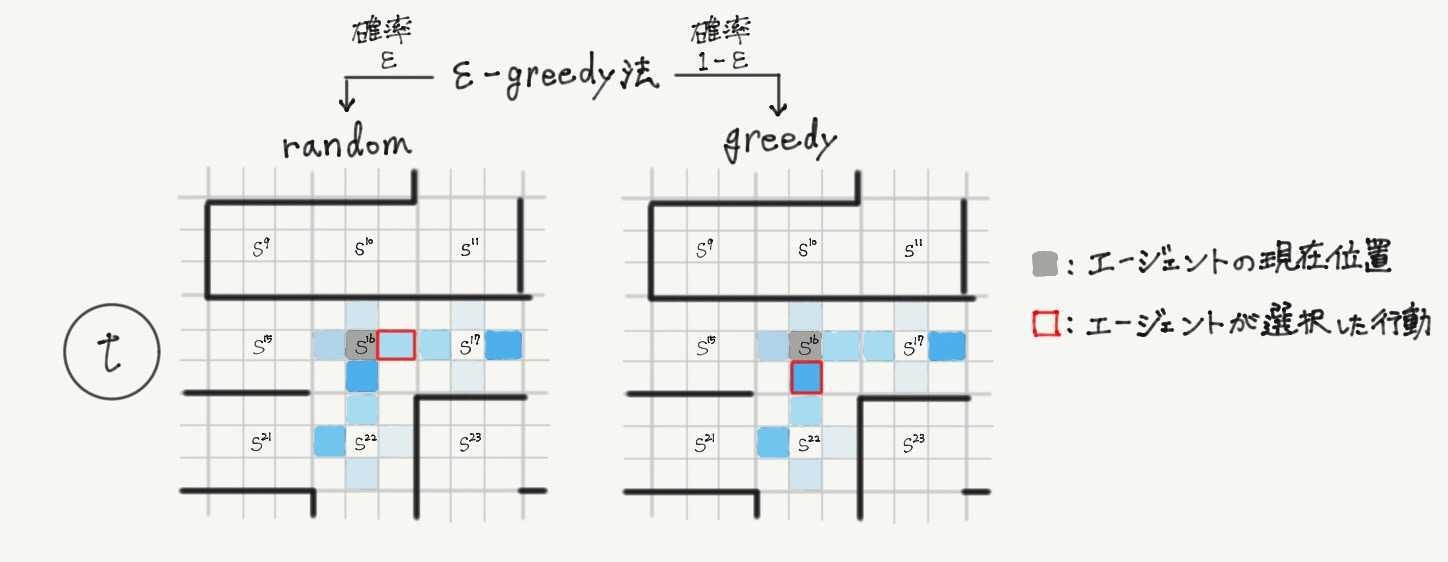
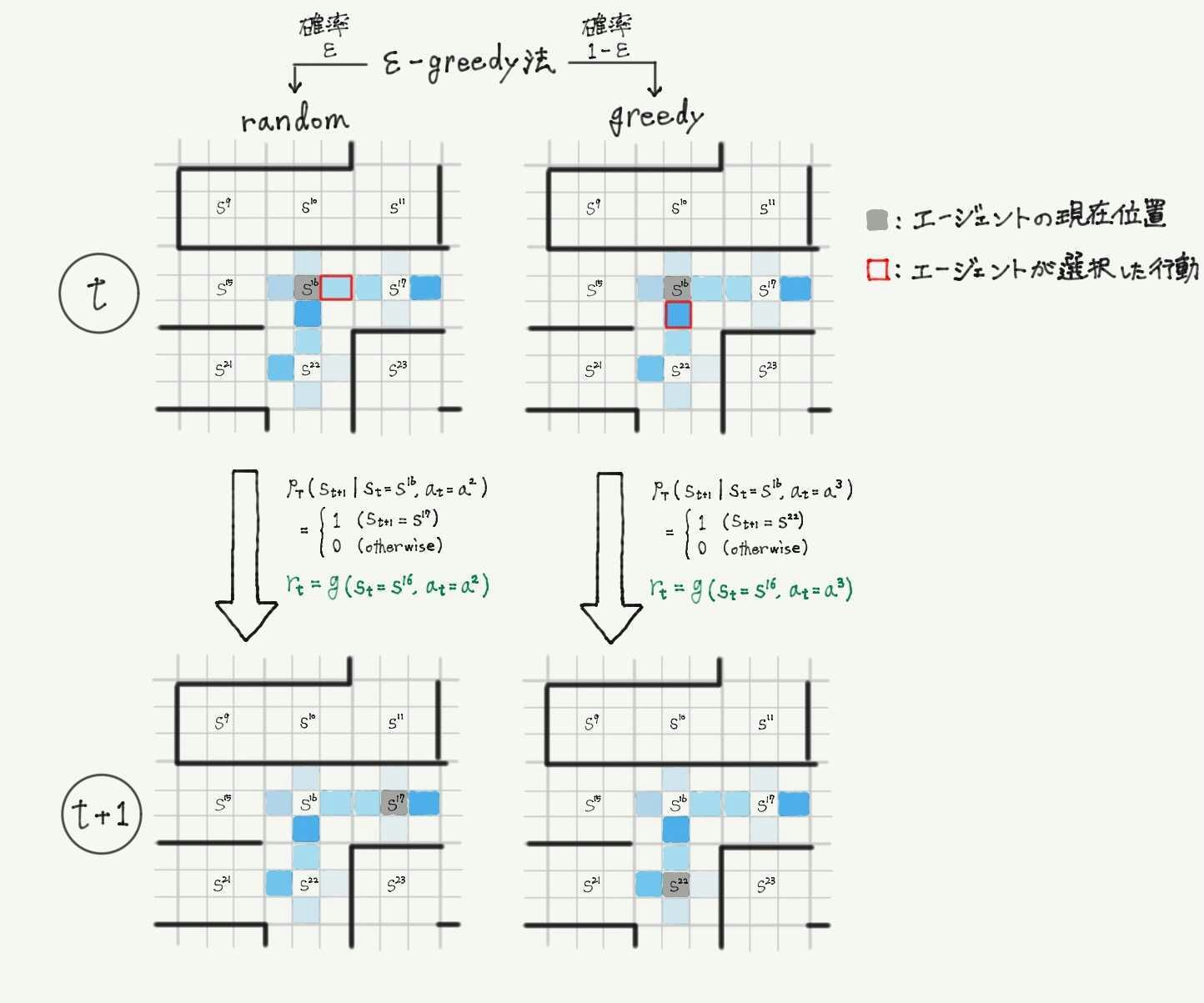
- 確率$\ \epsilon \ $でランダムに行動を選択、確率$\ 1-\epsilon \ $で状態行動価値関数の推定値$\ \hat{Q}(s_t,a_t) \ $が最大となる行動を選択(下の図は時刻$\ t \ $における例)
- 手順③
- 式$\ (\spadesuit) \ $の近似式を用いて、$\hat{Q}(s_t,a_t) \ $を更新
- 手順④
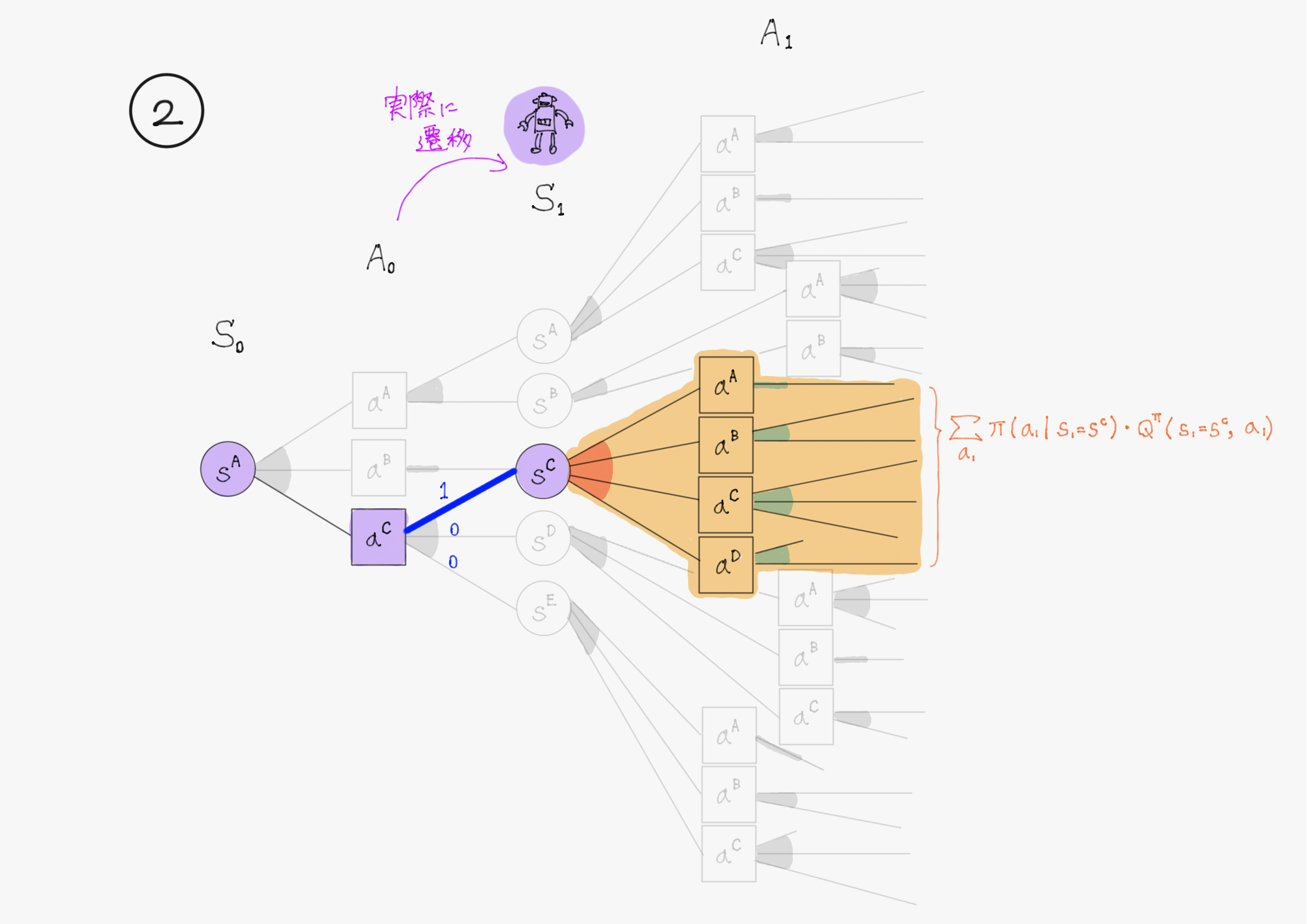
- 手順②と③を繰り返すと、最終的に状態行動価値関数は例えば下記のようになり、スタートから最大の値を辿っていけばゴールまでつくようになっている。
1.3 Q学習における方策
結論から言うと、手順2の部分が方策$\ \pi \ $になっている。
このような一定確率でランダムに、一定確率で貪欲に(推定されている価値に基づいて)行動する手法を**$\ \epsilon$-greedy法**と呼ぶ。
一般に強化学習では、「今までエージェントが訪れたことのない状態を探索すること」と「これまでの学習で得た価値の情報を活用して準最適な行動選択をする」ことのトレードオフが問題になる。(活用と探索のトレードオフ問題と呼ばれる)
$\epsilon$-greedy法は効率良く二つを両立できる代表的な方策の一つ。
「効率が良い」は誤り。@kngwyuさん、指摘ありがとうございました。
ちなみに数式で書くと以下のようになる
\pi (a \mid s) =
\begin{cases}
1-\epsilon+\frac{\epsilon}{\vert \mathcal{A} \vert} & \bigl(a=\underset{b \in \mathcal{A}}{\mathrm{argmax}}\hat{Q}(s_t, b) \bigr) \\
\frac{\epsilon}{\vert \mathcal{A} \vert} & (\text{otherwise})
\end{cases}
1.4 Q学習の更新
本節では、Q学習の更新式$\
\hat{Q}(s_t,a_t)
\approx
r_t + \gamma
\underset{b \in \mathcal{A}}{\max}
\hat{Q}(s_{t+1},b) \ $がBellman方程式からどのようにして導かれるかを解説する。
見やすさのため、元となるBellman方程式(式$\ (\spadesuit) \ $)を再掲しておく。
Q^\pi(s,a)
=
g(s,a) + \gamma
\sum_{s'}
p_{\mathrm{T}}(s' \mid s,a)
\cdot
\sum_{a'}
\pi(a’ \mid s')
\cdot
Q^\pi(s',a')
\qquad
-(\spadesuit)
まず、式$\ (\spadesuit) \ $第2項の$ \
\sum_{a'}
\pi(a’ \mid s')
\cdot
Q^\pi(s',a')
$の部分は、$\ a' \ $について和をとっているので$\ s' \ $のみに依存する関数であるとわかる。これを便宜上$\ f(s') \ $と置く。
すると$
\sum_{s'}
p_{\mathrm{T}}(s' \vert s,a)
\cdot
f(s')
\ $の部分は、定義より状態$\ s \ $で行動$\ a \ $を選択したときの$\ f(s') \ $の期待値を意味していることになる。
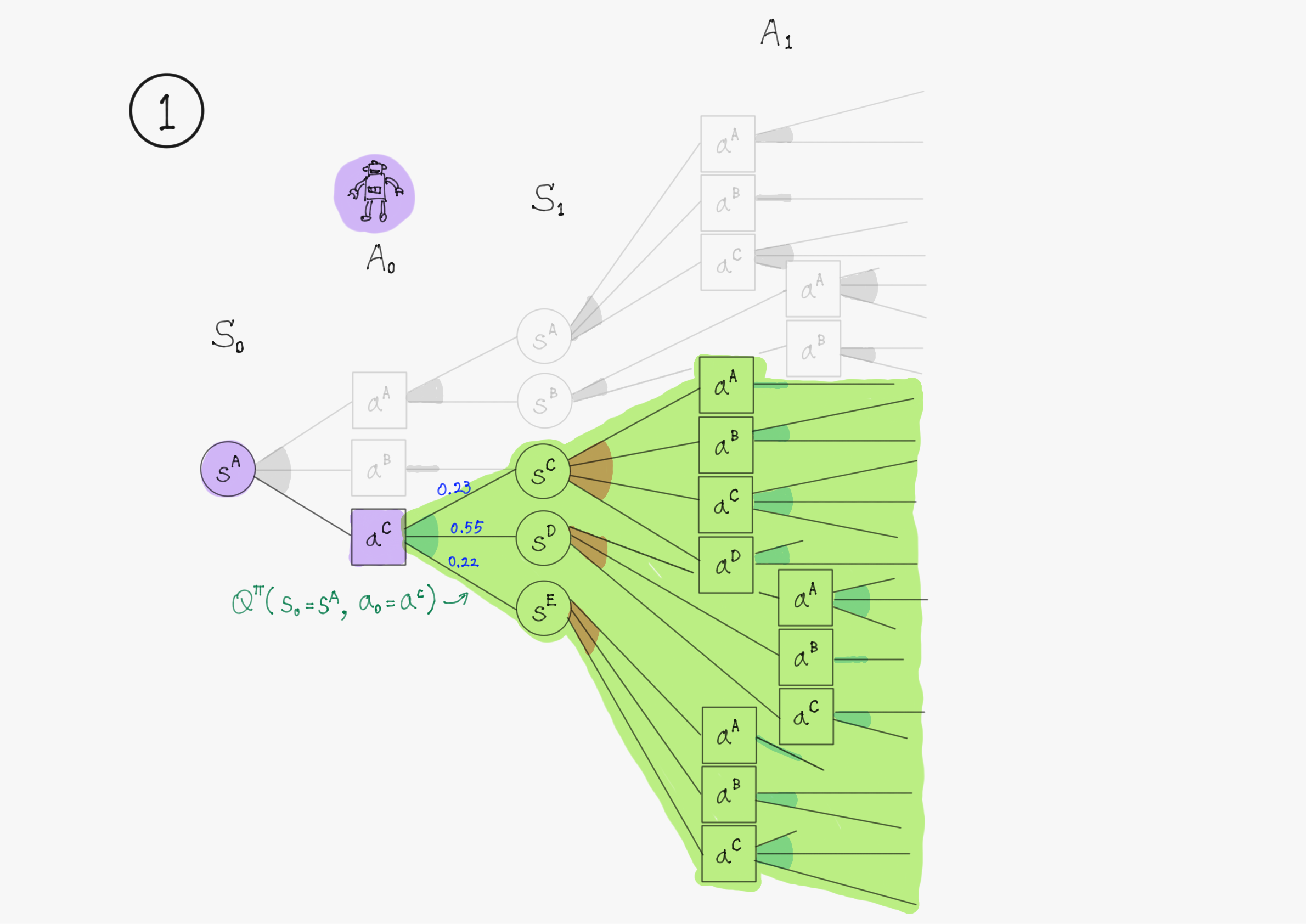
すなわち、式$\ (\spadesuit) \ $の第2項では、状態$\ s \ $で行動$a$を選択した際に遷移する可能性のある全ての状態$\ s' \ $について、$\ f(s') \ $の(その実現確率を考慮した)平均値を算出している。
Q学習ではまず、ここを実際に遷移した先の状態の値で近似している。
これは、状態$\ s \ $で行動$\ a \ $を選択した時に、実際に遷移した先の状態$\ s^* \ $の実現確率が$\ 1 \ $でそれ以外が$\ 0 \ $になるとして期待値を計算することに対応する。
式で書くと次の通り。
\begin{align}
\text{状態}\ s \ &\text{で行動}\ a \ \text{を選択し、状態}\ s^* \ \text{に遷移したとするとき、}\\
&p_{\mathrm{T}}(s' \vert s,a)
=
\begin{cases}
1 & (s'=s^*) \\
0 & (\text{otherwise})
\end{cases}
\\
\text{と考え}\\
&\sum_{s'}
p_{\mathrm{T}}(s' \vert s,a)
\cdot
\sum_{a'}
\pi(a’ \vert s')
\cdot
Q^\pi(s',a')
\rightarrow
\sum_{a'}
\pi(a’ \vert s^*)
\cdot
Q^\pi(s^*,a')
\end{align}
次に$\ f(s') = \sum_{a'} \pi(a’ \mid s') \cdot Q^\pi(s',a') \ $の近似を考える。
$\ f(s') \ $は、状態$\ s \ $で行動$\ a \ $をとり状態$\ s' \ $に遷移したとき、そこで方策$\ \pi \ $に従って行動選択した結果得られるであろう状態行動価値$\ Q^\pi(s',a') \ $の期待値を意味している。
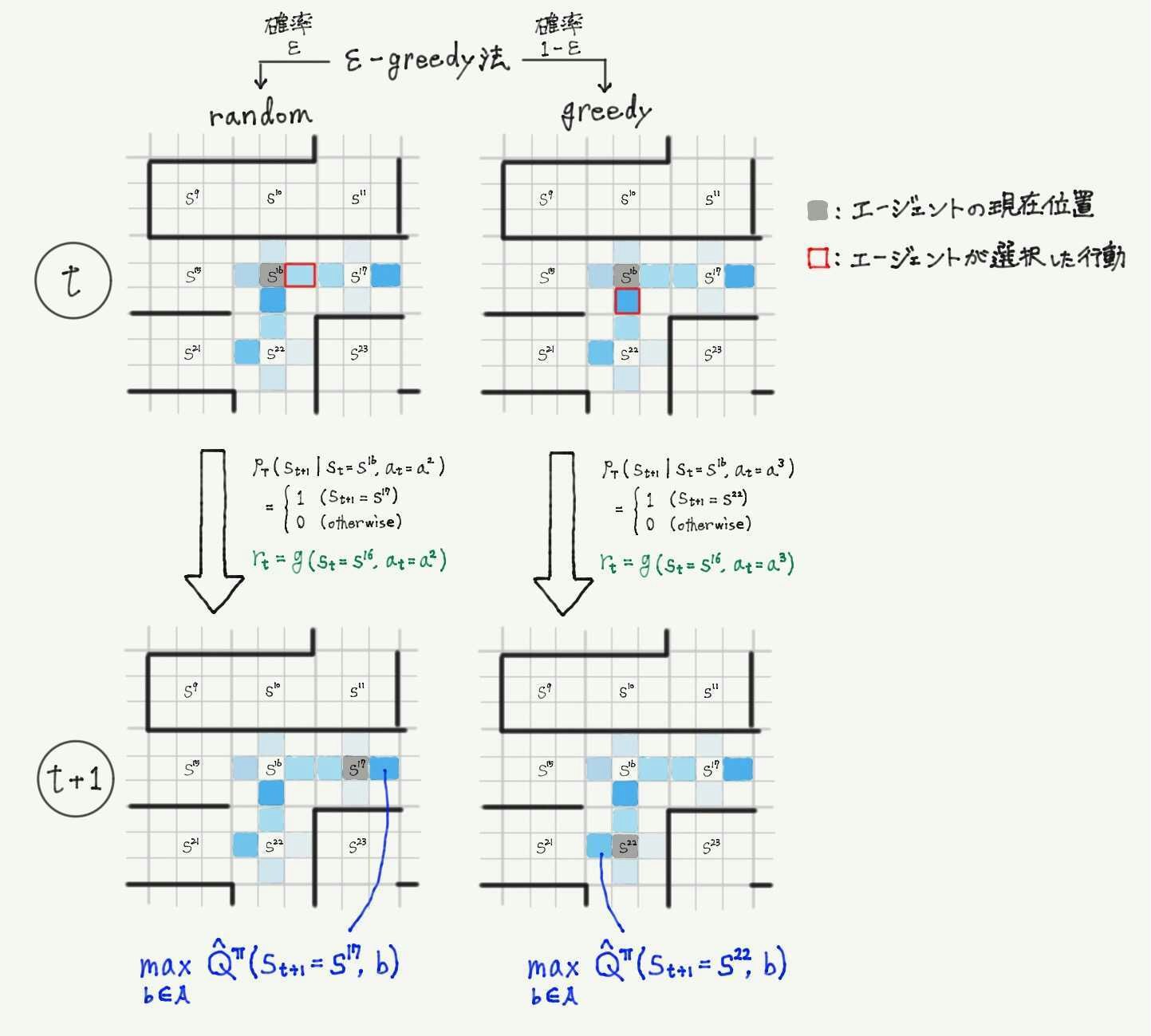
Q学習ではここをさらに状態行動価値$\ Q^\pi(s',a') \ $の最大値で近似する。
これは、例えば状態$\ s' \ $で取ることのできる行動が$\ a^1, \ a^2, \ a^3, \ a^4 \ $の4つだとして$\ Q^\pi(s',a^2) \ $が$\ Q^\pi(s',a^1), \ Q^\pi(s',a^2), \ Q^\pi(s',a^3), \ Q^\pi(s',a^4) \ $の中で最大の値を取ると仮定したとき、方策$\ \pi(a' \mid s') \ $が「$\ a' = a^2 \ $の時のみ確率が$\ 1 \ $でそれ以外の時$\ 0 \ $となるような確率分布」であるとして期待値を計算することに対応する。
式で書くと次の通り。
\begin{align}
\text{状態}\ s' \ \text{で可能な行動}\ &a’ \in \mathcal{A} \ \text{のうち、}\ a'=a^* \ \text{で最大の} \ Q^\pi(s',a') \ \text{が得られるとするとき、}\\
&\pi(a' \mid s')
=
\begin{cases}
1 & (a'=a^*) \\
0 & (\text{otherwise})
\end{cases}
\\
\text{と考え} \qquad \qquad \quad\\
&\sum_{a'}
\pi(a’ \vert s')
\cdot
Q^\pi(s',a')
\rightarrow
\underset{b \in \mathcal{A}}{\max}
Q^\pi(s',b)
\end{align}
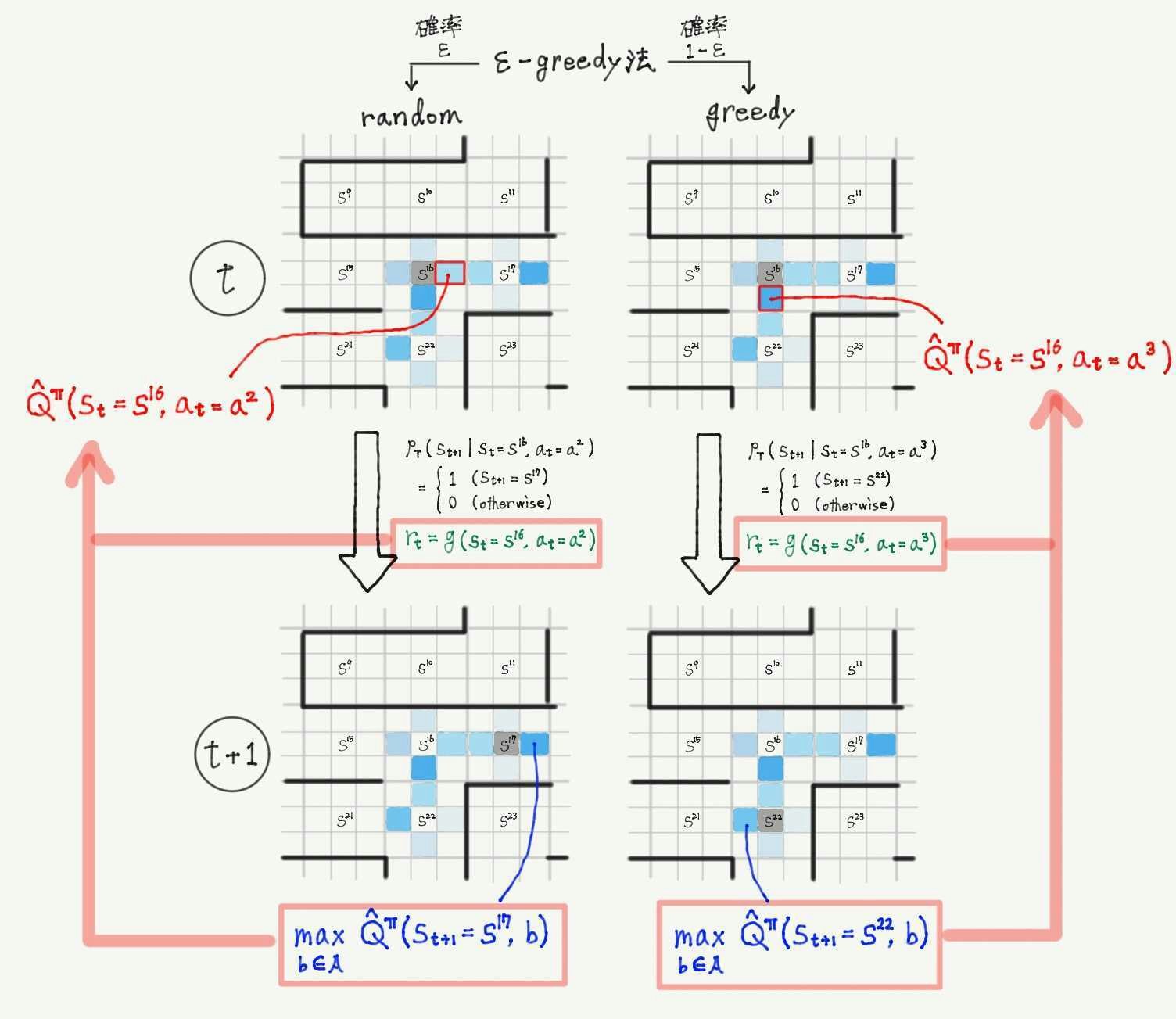
図で表すと、③を④で近似するというイメージ。③はわかりやすさのため②の図を書き換えただけ。
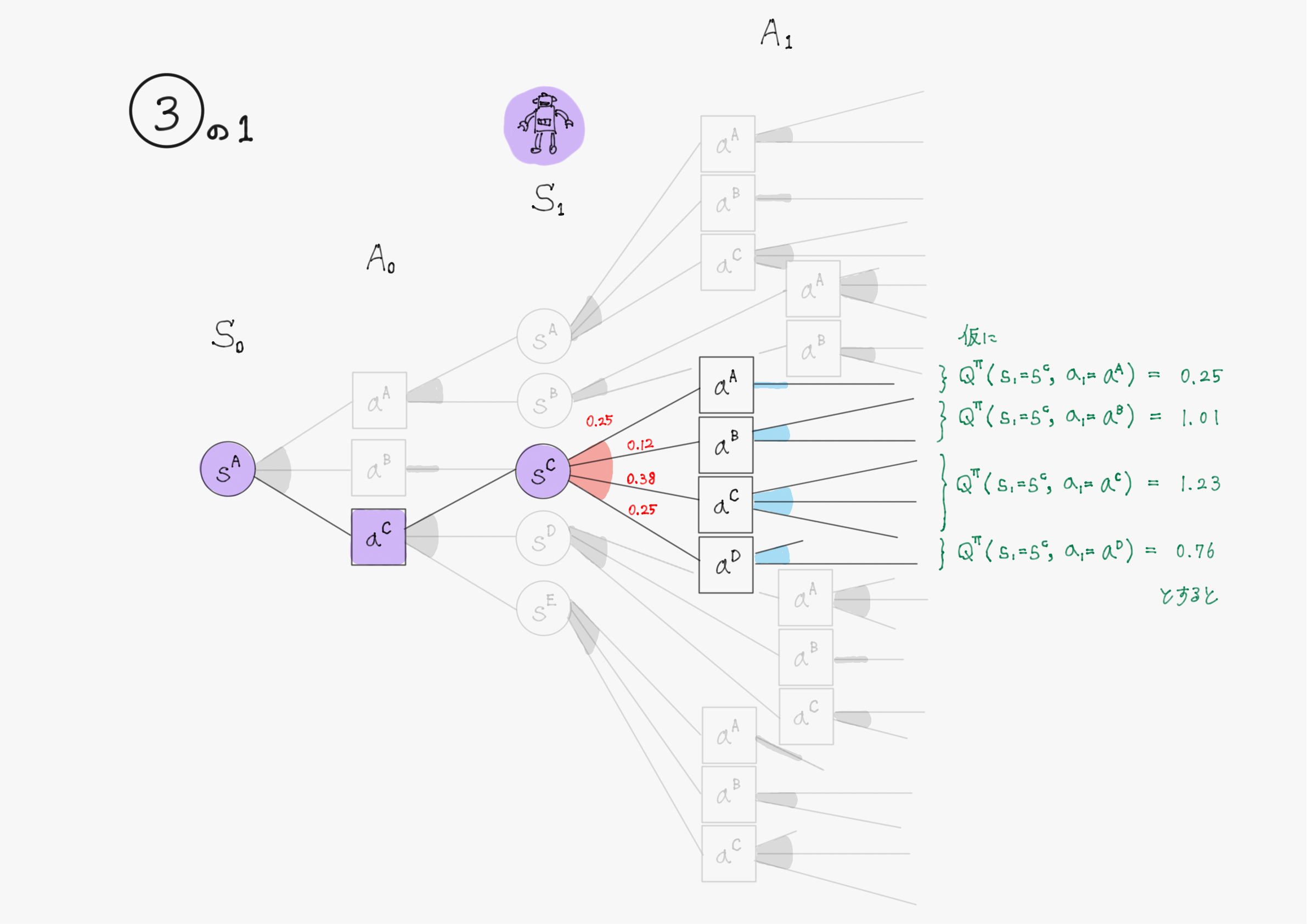
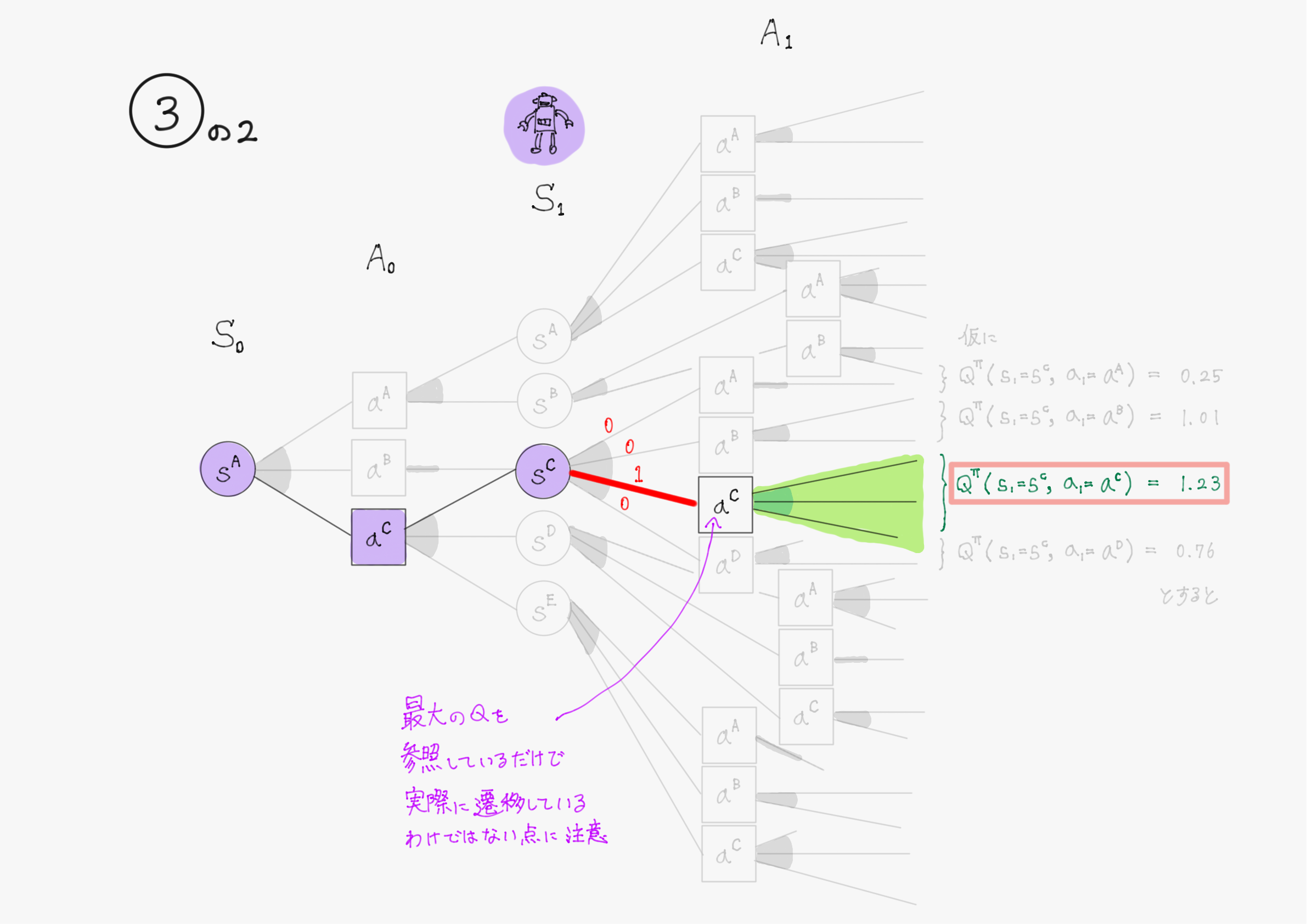
加えて、今$\ Q^\pi(s',a') \ $は正確には求まっていないため、推定値$\ \hat{Q}(s',a') \ $を使う。
\underset{b \in \mathcal{A}}{\max}
Q^\pi(s',b)
\rightarrow
\underset{b \in \mathcal{A}}{\max}
\hat{Q}(s',b)
従って、「状態$\ s \ $で行動$\ a \ $を取ったときの状態行動価値の推定値$\ \hat{Q}(s,a) \ $」は、実際に行動し報酬$\ r \ $を得て次状態$\ s' \ $に遷移したのちには次のような値で更新できる。(遷移後の状態$\ s' \ $やそこでの$\ \hat{Q}(s',a') \ $を更新に使うので、実際に1ステップだけエージェントが行動しないと、更新はできない)
r + \gamma
\underset{b \in \mathcal{A}}{\max}
\hat{Q}(s',b)
この「1ステップ時間が進みエージェントが環境と相互作用するたびに、$\ \hat{Q}(s,a) \ $の値を$\
r + \gamma
\underset{b \in \mathcal{A}}{\max}
\hat{Q}(s',b)
\ $で更新する」ことを初期状態$\ s_0 \ $から終端状態$\ s_K \ $まで行い、それを繰り返せば、いずれは全ての状態・行動のペア$\ (s,a) \ $について状態行動価値$\ \hat{Q}(s,a) \ $の値が収束し、Bellman方程式の近似解が求まる。
ここでは収束性の証明などはしないが、更新前よりも更新後の$\ \hat{Q}(s,a) \ $の値の方が正確である(解の値に近い)ことの直観的な説明は以下の通りである。
一般にある状態での将来の予測値よりも、実際に一つ未来のステップに進んで確定した情報が増えた状態での予測値の方が正確なため、エージェントが1ステップ行動して状態行動価値関数$\ \hat{Q}(s,a) \ $を更新する前と後では、強化学習における目的関数(最大化したいもの)である報酬$\ r \ $を環境から確定情報としてエージェントが得ている分、後の方がより正確に$\ Q^\pi(s,a) \ $を推定できているはずである。
実際には、学習を安定させるため、
- 「行動して報酬を受け取る前」の推定値である$\ \hat{Q}(s,a)$
- 「行動して報酬を受け取った後」の推定値である$\ r + \gamma \underset{a^i \in \mathcal{A}}{\max} \hat{Q}(s',a^i)$
の内分値が更新後の値として扱われ、その内分比率を決定するパラメータ$\ \alpha \ $を(どれぐらい急激に更新するかを決めるので)学習率と呼ぶ。
$$
\hat{Q}(s,a)
\longleftarrow
(1-\alpha) \cdot \hat{Q}(s,a)
+
\alpha \cdot \left(
r + \gamma
\underset{a^i \in \mathcal{A}}{\max}
\hat{Q}(s',a^i)
\right)
$$
2. Q学習を用いた迷路探索の実装
第2章では、第1回、第2回を通して定式化した迷路を環境として定義し、Q学習を用いてこれを踏破可能なエージェントを訓練することを試みる。
コードはこちら。Colabで実装したので、誰でも簡単に試すことができる。
ただし、初回のみGoogle Driveにマウントして作成したフォルダに迷路マップ作成に必要な画像を入れる必要があるので注意(脳死で全て実行をするとエラーが出る)。また描画に時間がかかるため、すべて実行すると3時間程度かかるので注意。
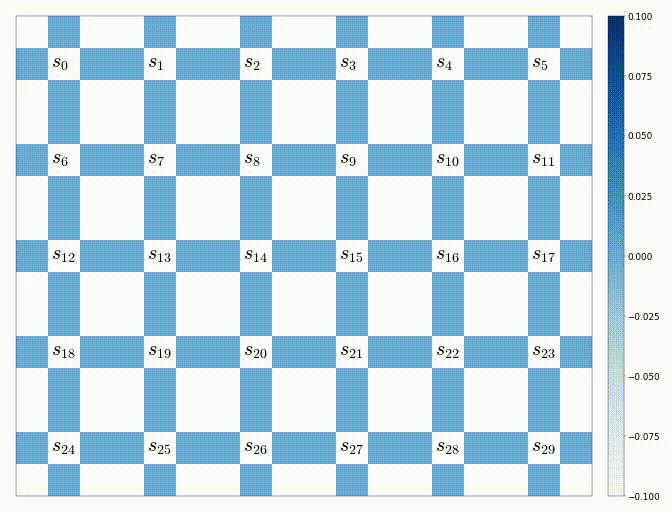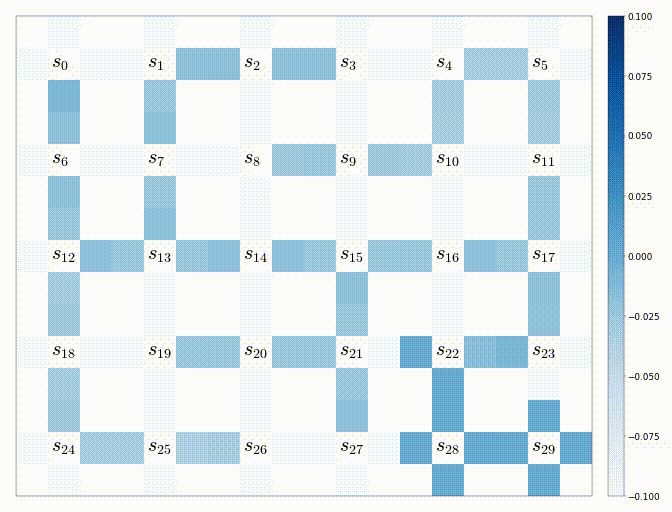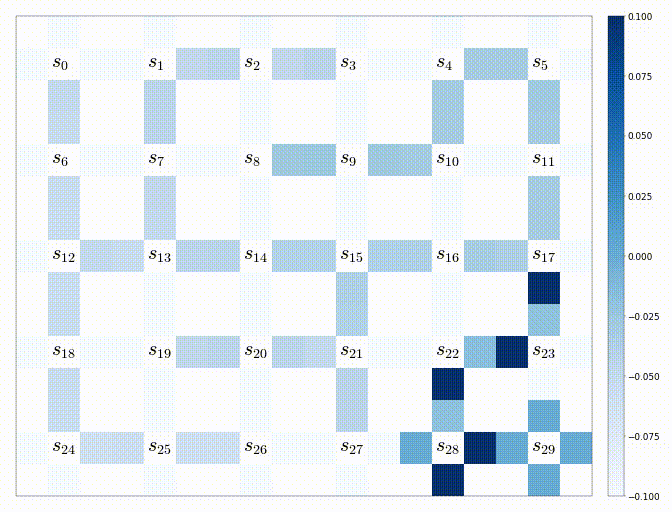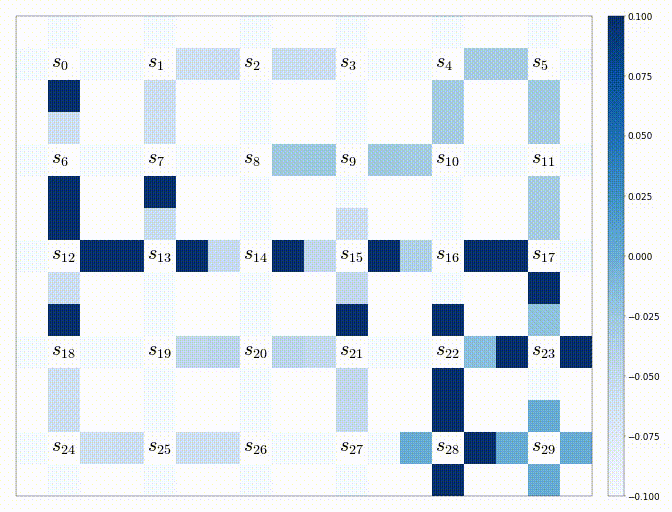
結果の可視化に力を入れ、エージェントが迷路を「踏破」している感じやQ値がどのように更新されているかがわかりやすいように配慮したつもりである。
学生用に実験を用意しているが、実験1では環境からの報酬情報が増えた時にエージェントの学習にどのような影響を及ぼすかを、実験2では正の報酬がスパースな環境では探索空間が広くなると学習がうまくいかなくなる可能性があることを割引率の大きさを変えて実験している。(実験2は勝手に考えた実験なので、他で見たことはないですが、、、)
うまく動けば、下記のような結果が生成されるはずである。(以下は上記のコードの実験1-3の結果である)
参考文献
- 森村哲郎, 強化学習, 機械学習プロフェッショナルシリーズ, 講談社, 2019.
おわりに
最後の方(特にQ学習のコードについて)は説明が雑になってしまいましたが、なんとか書き上げることができました。
TAを担当した授業では本当はDQNまで扱ったのですが、資料の整理ができていないので今回はここまでとさせていただきます。
最後に、ここまで読んでくださった方、本当にありがとうございました。初めての記事執筆でしたので色々と至らないところもあったと思いますが、何か間違いや修正案などありましたらコメントいただけると幸いです。