概要
TensorFlowに導入されているEager Modeについて、プログラムの書き方を理解するため、Kerasとの書き方の比較をしてみました。また、学習結果の差がどうなるかを検証しました。
環境
TensorFlow v1.10
Windows10
Eager Modeの起動
まずは、TensorFlowをEagerModeに切り替えます。KerasはEagerModeにしておいても動くようです。
import tensorflow as tf
tf.enable_eager_execution()
tfe = tf.contrib.eager
print("TensorFlow version: {}".format(tf.VERSION)) # TensorFlowのバージョン確認
print("Eager execution: {}".format(tf.executing_eagerly())) # Eager Modeになっていることの確認
データの準備
APIの検証をしたいだけなので、学習時間の短いIrisデータを使います。Irisデータの場合、scikit-learnのAPIを使うのが便利。
from sklearn import datasets, preprocessing, model_selection
iris = datasets.load_iris()
all_x = preprocessing.scale(iris.data).astype('float32') # データのスケーリングと標準化
all_y = iris.target
# 訓練データと検証データに分割(8割(120サンプル)を訓練データに)
train_x, val_x, train_y, val_y = model_selection.train_test_split(all_x, all_y, train_size=0.8)
モデルの定義
学習にはシンプルな全結合ニューラルネットワークを使います。
from tensorflow import keras
def get_model():
model = tf.keras.Sequential([
tf.keras.layers.Dense(10, activation=tf.nn.relu, input_shape=(4,)),
tf.keras.layers.Dense(10, activation=tf.nn.relu),
tf.keras.layers.Dense(3, activation=tf.nn.softmax)
])
return model
最適化条件
なんでも良いですが、シンプルにSDGを使うことにします。エポック数、バッチサイズもここで定義しておきます。
def get_optimizer():
return tf.train.GradientDescentOptimizer(learning_rate=0.01)
batch_size = 32
num_epochs = 1000
学習
まずは、Kerasでの学習をしてみます。出力結果は、後ほど、Eager Modeとの比較で示します。
def keras_training():
model = get_model()
optimizer = get_optimizer()
model.compile(loss=keras.losses.sparse_categorical_crossentropy,
optimizer=optimizer,
metrics=['accuracy'])
hist = model.fit(train_x, train_y, epochs=num_epochs, batch_size=batch_size, validation_data=(val_x, val_y))
return hist
keras_hist = keras_training()
Eager Modeでの学習
主な相違点は以下の3点です、それぞれについて説明します。
- データはDatasetクラスで扱う
- モデル・損失関数の定義
- 学習ループを自分で記述する
Dataの準備
Eager Modeの学習のためには、TensorFlowのDataset形式である必要があるようです。Datasetはいろいろな作り方がありますが、Numpyの配列からはfrom_tensor_slicesを使って、以下のように変換できます。
from tensorflow.data import Dataset
train_dataset = Dataset.from_tensor_slices((train_x, train_y)).batch(batch_size)
val_dataset = Dataset.from_tensor_slices((val_x, val_y)).batch(batch_size)
モデル・損失関数・勾配の定義
Kerasの標準的な損失関数はsoftmaxの出力を入力として、算出されますが、TensorFlowの場合は、softmaxを通さない出力(Logits)を入力し、損失関数の中でsoftmaxを算出するのが標準のようです。
したがって、モデルとしてはsoftmaxを通さないモデルを定義します。
def get_model_wo_softmax():
model = tf.keras.Sequential([
tf.keras.layers.Dense(10, activation=tf.nn.relu, input_shape=(4,)),
tf.keras.layers.Dense(10, activation=tf.nn.relu),
tf.keras.layers.Dense(3)
])
return model
def loss(model, x, y):
logits = model(x)
return tf.losses.sparse_softmax_cross_entropy(labels=y, logits=logits)
def grad(model, inputs, targets):
with tf.GradientTape() as tape:
loss_value = loss(model, inputs, targets)
return loss_value, tape.gradient(loss_value, model.trainable_variables)
学習の仕方
学習ループをfor文を使って自分で書きます。今回のように、単純なニューラルネットを最適化するだけだと、あまりメリットはないでしょうが、より複雑な手順で学習したい時にはメリットがありそうです。
def eager_training():
model = get_model_wo_softmax()
optimizer = get_optimizer()
global_step = tf.train.get_or_create_global_step()
# 損失関数の値・精度を残しておくためのリスト
train_loss_list = []
train_accuracy_list = []
val_loss_list = []
val_accuracy_list = []
for epoch in range(num_epochs):
epoch_loss_avg = tfe.metrics.Mean()
epoch_accuracy = tfe.metrics.Accuracy()
# 学習のループ
for b, (x, y) in enumerate(train_dataset):
loss_value, grads = grad(model, x, y)
optimizer.apply_gradients(zip(grads, model.variables),
global_step)
epoch_loss_avg(loss_value) # add current batch loss
epoch_accuracy(tf.argmax(model(x), axis=1, output_type=tf.int32), y)
train_loss_list.append(epoch_loss_avg.result())
train_accuracy_list.append(epoch_accuracy.result())
# 検証のループ
epoch_test_loss_avg = tfe.metrics.Mean()
epoch_test_accuracy = tfe.metrics.Accuracy()
for b, (x, y) in enumerate(val_dataset):
epoch_test_loss_avg(loss(model, x, y))
epoch_test_accuracy(tf.argmax(model(x), axis=1, output_type=tf.int32), y)
val_loss_list.append(epoch_test_loss_avg.result())
val_accuracy_list.append(epoch_test_accuracy.result())
return train_loss_list, train_accuracy_list, val_loss_list, val_accuracy_list
train_loss_results, train_accuracy_results, val_loss_results, val_accuracy_results = eager_training()
KerasとEager Modeの結果比較
気になるのは、ちゃんと結果が一致するのかというところです。そのために比較をしてみます。
学習曲線の比較
学習曲線を比較すると、およそ一致することがわかります。
import matplotlib.pyplot as plt
import numpy as np
x = range(num_epochs)
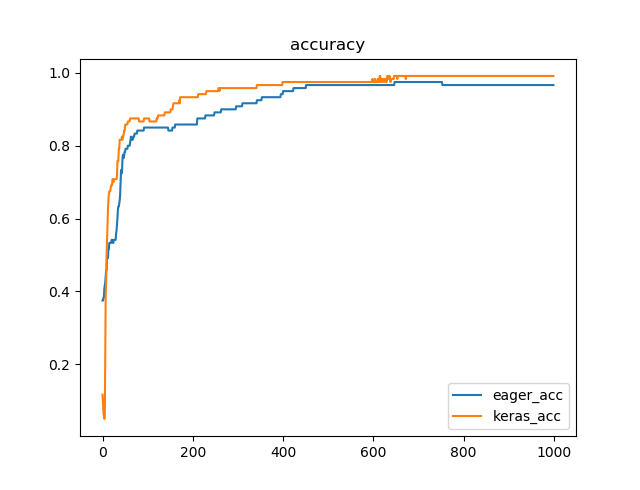
plt.plot(x, train_accuracy_results, label="eager_acc")
plt.plot(x, keras_hist.history['acc'], label="keras_acc")
plt.title("accuracy")
plt.legend(loc='best')
plt.show()
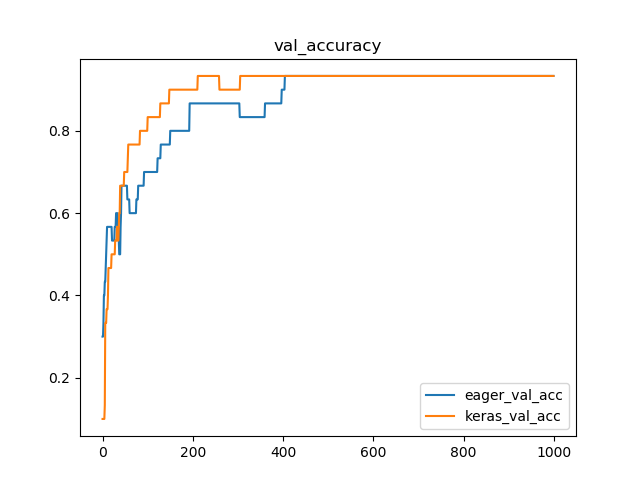
plt.plot(x, val_accuracy_results, label="eager_val_acc")
plt.plot(x, keras_hist.history['val_acc'], label="keras_val_acc")
plt.title("val_accuracy")
plt.legend(loc='best')
plt.show()
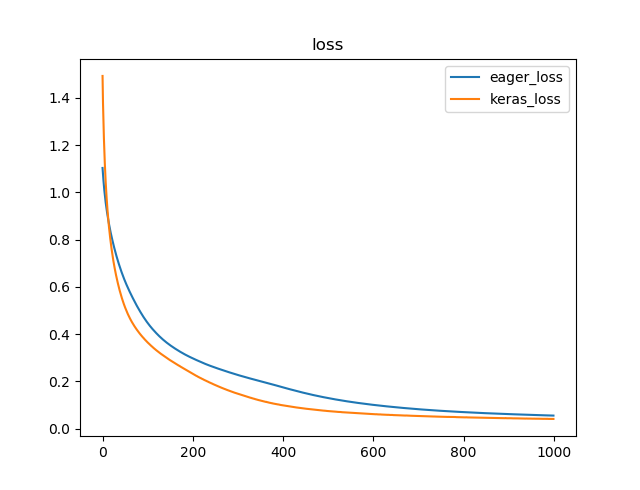
plt.plot(x, train_loss_results, label="eager_loss")
plt.plot(x, keras_hist.history['loss'], label="keras_loss")
plt.title("loss")
plt.legend(loc='best')
plt.show()
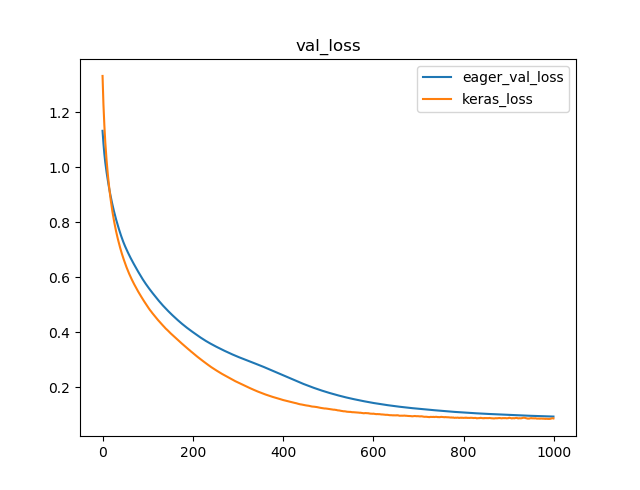
plt.plot(x, val_loss_results, label="eager_val_loss")
plt.plot(x, keras_hist.history['val_loss'], label="keras_loss")
plt.title("val_loss")
plt.legend(loc='best')
plt.show()
訓練データでの損失関数の値(横軸Epoch数)
検証データでの損失関数の値(横軸Epoch数)
訓練データに対する精度(横軸Epoch数)
検証データに対する精度(横軸Epoch数)
損失関数の差分
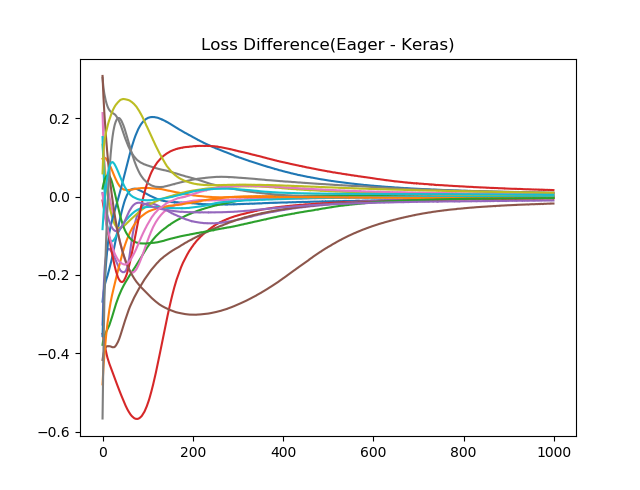
乱数が毎回違うためか、結果が完全には一致をしないので、KerasとEager Modeの差分を20回取って、プロットしてみます。序盤では差が出ることがわかりますが、Epochを進めると、結果が一致してくることがわかります。(もう少しEpoch増やしてみたほうがよかったかもしれません。)
val_loss_difference = []
loss_difference = []
for i in range(20):
keras_hist = keras_training()
train_loss_results, train_accuracy_results, val_loss_results, val_accuracy_results = eager_training()
loss_difference.append(np.array(train_loss_results) - np.array(keras_hist.history['loss']))
val_loss_difference.append(np.array(val_loss_results) - np.array(keras_hist.history['val_loss']))
for item in loss_difference:
plt.plot(item)
plt.title("Loss Difference(Eager - Keras)")
plt.show()
for item in val_loss_difference:
plt.plot(item)
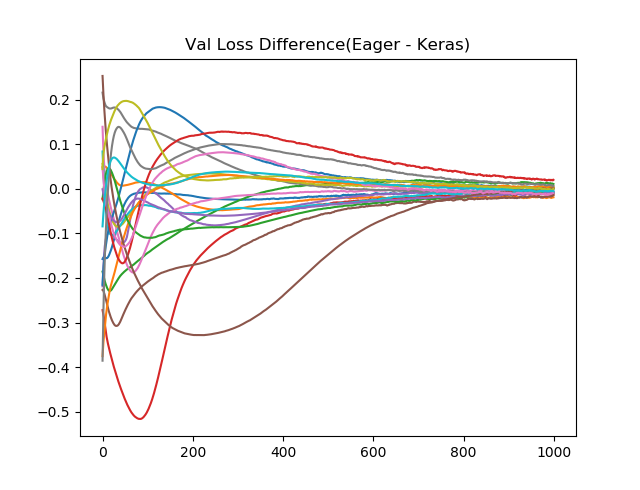
plt.title("Val Loss Difference(Eager - Keras)")
plt.show()
訓練データに対する損失関数値の差(横軸Epoch数)
検証データに対する損失関数値の差(横軸Epoch数)
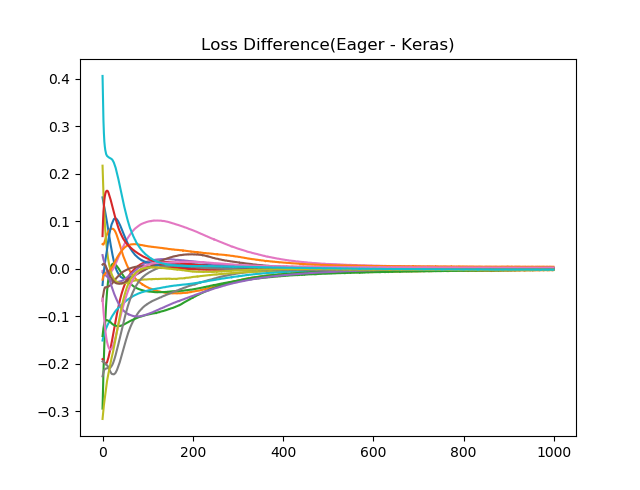
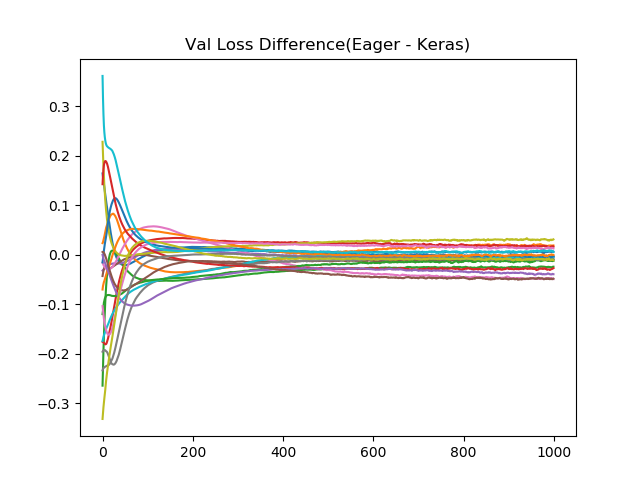
損失関数の差分(中間層のユニット数:30の場合)
結果が安定することを期待して、中間層のユニット数を10から30に増加させると、1000Epoch学習後のばらつきは小さくなっているように見えます。(縦軸のスケールが違うことに注意。検証データのほうはあまり変わらないかも。)