1. 概要
-
その5に引き続き『経済・ファイナンスデータの計量時系列分析』を元に勉強中。
- 本稿は第6章の見せかけの回帰と共和分について
2. 見せかけの回帰
定義
2つの無関係な単位根過程$x_t$と$y_t$について、$y_t=\alpha+\beta x_t+\epsilon_t$との回帰をした時に、$x_t$と$y_t$の間に有意な関係があるように見える現象を見せかけの回帰という。
検証
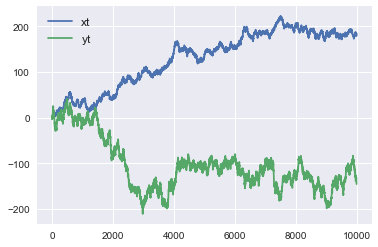
- 2つの独立な過程
$\qquad x_t=x_{t-1}+\epsilon_{x,t}, \quad \epsilon_{x,t}\sim iid(0,\sigma_x^2)$
$\qquad y_t=y_{t-1}+\epsilon_{y,t}, \quad \epsilon_{y,t}\sim iid(0,\sigma_y^2)$
をつくり、
$\qquad y_t=\alpha+\beta x_t+\epsilon_t$
というモデルに回帰する。
# データ生成
sigma_x, sigma_y = 1, 2
T = 10000
xt = np.cumsum(np.random.randn(T) * sigma_x).reshape(-1, 1)
yt = np.cumsum(np.random.randn(T) * sigma_y).reshape(-1, 1)
from sklearn.linear_model import LinearRegression
reg = LinearRegression().fit(xt,yt)
print('R-squared : ',reg.score(xt,yt))
print('coef : ',reg.coef_, 'intercept', reg.intercept_)
R-squared : 0.4794854506874714
coef : [[-0.62353254]] intercept [-24.27600549]
- 決定係数($R^2$)は0.479と、そこそこ高い値となった。回帰モデルについては、$\alpha=-24.28,\quad \beta=-0.6235$という形になった。
- $x_t$と$y_t$が独立であるかどうかを検定するためには$H_0 : \beta=0$を検定したい。しかし、scikit-learnにはそこまでの機能が見つからなかった。
- 他のライブラリを探したところ、statsmodelsが便利そうだったので、statsmodelsで再度回帰を行なった。
import statsmodels.api as sm
reg = sm.OLS(yt,sm.add_constant(xt,prepend=False)).fit()
reg.summary()
|
|
|
|
| Dep. Variable: |
y |
R-squared: |
0.479 |
| Model: |
OLS |
Adj. R-squared: |
0.479 |
| Method: |
Least Squares |
F-statistic: |
9210. |
| Date: |
Tue, 07 Jan 2020 |
Prob (F-statistic): |
0.00 |
| Time: |
22:36:57 |
Log-Likelihood: |
-51058. |
| No. Observations: |
10000 |
AIC: |
1.021e+05 |
| Df Residuals: |
9998 |
BIC: |
1.021e+05 |
| Df Model: |
1 |
|
|
| Covariance Type: |
nonrobust |
|
|
|
coef |
std err |
t |
P>abs(t) |
[0.025 |
0.975] |
| const |
-24.2760 |
0.930 |
-26.113 |
0.000 |
-26.098 |
-22.454 |
| x1 |
-0.6235 |
0.006 |
-95.968 |
0.000 |
-0.636 |
-0.611 |
- add_constantは回帰モデルに定数項(先ほどの回帰式でいう$\alpha$)を含めるかどうかに関わるところである。add_constantしてやることで、回帰モデルに定数項を含めることになる。なお、scikit-learnの場合は、fit_interceptという引数をFalseにしてやると、定数項のない回帰となる。上ではこれを明示していないが、fit_intercept=Trueがデフォルト値だからである。
- scikit-learnの時と同様に決定係数は0.479、$\alpha=-24.28,\quad \beta=-0.6235$となり、同等の回帰ができていることが確認できた。
- statsmodelsのいいところは、95%有意水準の値を出してくれるところである。これを見ると$H_0 : \beta=0$に関して、95%有意水準では-0.636以上-0.611以下にならなくてはならないため、$H_0$は棄却されることとなる。これが見せかけの回帰である。
回避する方法
ラグ変数をモデルに含める
- 回帰するモデルを以下のように変更する。
$\qquad y_t=\alpha+\beta_1 x_t+\beta_2 y_{t-1}+\epsilon_t$
$y_t$の説明変数に$y_{t-1}$を加えている。
statsmodelsを使って回帰する場合、以下のようになる。sm.OLSが引数に被説明変数、説明変数を取るが、説明変数は以下のようにひとつの配列にまとめてフィードしてやる必要がある。
x_t, y_t, y_t_1 = xt[1:], yt[1:], yt[:-1]
X = np.column_stack((x_t, y_t_1))
reg = sm.OLS(y_t,sm.add_constant(X)).fit()
reg.summary()
|
|
|
|
| Dep. Variable: |
y |
R-squared: |
0.999 |
| Model: |
OLS |
Adj. R-squared: |
0.999 |
| Method: |
Least Squares |
F-statistic: |
3.712e+06 |
| Date: |
Thu, 09 Jan 2020 |
Prob (F-statistic): |
0.00 |
| Time: |
22:12:59 |
Log-Likelihood: |
-21261. |
| No. Observations: |
9999 |
AIC: |
4.253e+04 |
| Df Residuals: |
9996 |
BIC: |
4.255e+04 |
| Df Model: |
2 |
|
|
| Covariance Type: |
nonrobust |
|
|
|
coef |
std err |
t |
P>abs(t) |
[0.025 |
0.975] |
| const |
-0.0815 |
0.049 |
-1.668 |
0.095 |
-0.177 |
0.014 |
| x1 |
-0.0004 |
0.000 |
-0.876 |
0.381 |
-0.001 |
0.000 |
| x2 |
0.9989 |
0.001 |
1964.916 |
0.000 |
0.998 |
1.000 |
- 先のモデルでいうと、$\alpha=-0.0815,\quad \beta_1=-0.0004, \quad \beta_2=0.9989$という結果が得られた。$\alpha$と$\beta_1$はほぼ0になっており、ほとんどが$y_{t-1}$で説明ができている。そして相関係数は0.999と限りなく1に近い値となっている。また、$H_0 : \beta_1=0$が棄却されない点にも注目である。
単位根過程の差分を取り定常過程にしてから回帰をする
- 回帰するモデルを以下のように変更する。
$\qquad \Delta y_t=\alpha+\beta \Delta x_t+\epsilon_t$
x_t, y_t = np.diff(xt.flatten()).reshape(-1,1), np.diff(yt.flatten()).reshape(-1,1)
reg = sm.OLS(y_t,sm.add_constant(x_t)).fit()
reg.summary()
|
|
|
|
| Dep. Variable: |
y |
R-squared: |
0.000 |
| Model: |
OLS |
Adj. R-squared: |
0.000 |
| Method: |
Least Squares |
F-statistic: |
3.297 |
| Date: |
Thu, 09 Jan 2020 |
Prob (F-statistic): |
0.0694 |
| Time: |
22:33:26 |
Log-Likelihood: |
-21262. |
| No. Observations: |
9999 |
AIC: |
4.253e+04 |
| Df Residuals: |
9997 |
BIC: |
4.254e+04 |
| Df Model: |
1 |
|
|
| Covariance Type: |
nonrobust |
|
|
| coef |
std err |
t |
P>abs(t) |
[0.025 |
0.975] |
| const |
-0.0138 |
0.020 |
-0.681 |
0.496 |
-0.054 |
| x1 |
-0.0374 |
0.021 |
-1.816 |
0.069 |
-0.078 |
- こちらのケースでは相関係数は0となり、$\beta=-0.0374$とほぼ0になっている。$H_0 : \beta_1=0$を棄却することもできず、$\Delta x_t$と$\Delta y_t$に有意な関係はないという結論が導かれる。
3. 共和分
定義
- $x_t$と$y_t$を単位根過程($\rm I(1)$)とする。このとき、$a x_t + b y_t \sim \rm I(0)$のように定常過程となる$a$と$b$が存在する時、$x_t$と$y_t$には共和分の関係がある。また、$(a,b)'$は共和分ベクトルと呼ぶ。
- より一般的には、$\mathbb y_t \sim \rm I(1)$について、$\mathbb a' \mathbb y_t \sim \rm I(0)$となるような$\mathbb a$が存在するとき、$\mathbb y_t$には共和分の関係がある。また、$\mathbb a$は共和分ベクトルと呼ぶ。
- 例えば、$u_{1t},u_{2t}$を互いに独立な定常過程、$w_{1t},w_{2t}$を互いに独立な単位根過程として、
$\qquad \left\{\begin{array}{ll}x_t = \alpha w_{1t} + u_{1t}\\ y_t = \beta w_{1t} + u_{2t} \end{array}\right.$
を考えてみる。このとき、$x_t$も$y_t$も$\rm I(1)$過程となるが、
$\qquad x_t - \frac{\alpha}{\beta}y_t = u_{1t} - \frac{\alpha}{\beta}u_{2t} \sim \rm I(0)$
となるので、$x_t$と$y_t$には共和分関係が存在し、共和分ベクトルは$(1,-\frac{\alpha}{\beta})'$となる。
インプリケーション
- $x_t$と$y_t$が単位根過程のとき、$x_t$と$y_t$の長期的な予測の誤差は大きくなっていってしまう。
- しかし、$x_t$と$y_t$の間に共和分関係がある場合、$z_t = y_t - a x_t$が定常過程となるような$a$が存在し、このとき$z_t$の長期的な予測を行うことは一定の精度で可能となる。
Granger表現定理
- 共和分関係を含んだVARモデルがベクトル誤差修正モデル(VECM)で表現できるというものである。
- VAR(p)表現を持つ共和分システム$\mathbb y_t$について、
$\qquad \begin{align} \Delta \mathbb y_t &= \zeta_1 \Delta \mathbb y_{t-1} + \zeta_2 \Delta \mathbb y_{t-2} + \cdots + \zeta_{p-1} \Delta \mathbb y_{t-p+1} + \mathbb \alpha + \zeta_0 \Delta \mathbb y_{t-1} + \epsilon_t \\ &= \zeta_1 \Delta \mathbb y_{t-1} + \zeta_2 \Delta \mathbb y_{t-2} + \cdots + \zeta_{p-1} \Delta \mathbb y_{t-p+1} + \mathbb \alpha + -\mathbb B \mathbb A' \mathbb y_{t-1} + \epsilon_t \end{align}$
というVECM(p-1)で表現できる。
- $-\mathbb B \mathbb A' \mathbb y_{t-1}$という項は誤差修正項と呼ばれる。ここで、$\mathbb A$は共和分ベクトルを表しており、誤差修正項は均衡からの乖離が大きくなった時、均衡に戻る力が働いていることを表している。
