1. 概要
- その4に引き続き『経済・ファイナンスデータの計量時系列分析』を元に勉強中。
- 本稿は第5章の単位根過程について
2. 単位根過程とは
- 非定常過程$y_t$の差分系列$\Delta y_t=y_t-y_{t-1}$が定常過程であるとき、$y_t$は単位根過程である。
- d階差分をとった系列が定常かつ反転可能なARMA(p,q)過程に従う時、この過程はARIMA(p,d,q)過程と呼ばれる。
3. 単位根検定
DF検定
- Dickey-Fuller(DF)検定は、真のモデルが単位根AR(1)過程であるという帰無仮説を、過程が定常AR(1)過程であるという対立仮説に対して検定する。
- [Case 1] : データがトレンドを持たず、過程の期待値が0の場合。
$\quad H_0:y_t=y_{t-1}+u_t, \quad H_1:y_t=\rho y_{t-1}+u_t, |\rho|<1$ - [Case 2] : データがトレンドを持たず、過程の期待値が0でない場合。
$\quad H_0:y_t=y_{t-1}+u_t, \quad H_1:y_t=\alpha + \rho y_{t-1}+u_t, |\rho|<1$ - [Case 3] : データがトレンドを持つ場合。
$\quad H_0:y_t=\alpha+y_{t-1}+u_t, \quad H_1:y_t=\alpha + \rho y_{t-1}+\delta t+u_t, |\rho|<1$ - 対立仮説のモデルをOLSで推定し、検定統計量$\tau_{\rho}$や$\tau_{t}$の値を算出する。その後対応するDF分布の棄却点と比較し、帰無仮説を棄却するかどうかを判断する。
- [Case 1]を元に検定統計量を示しておく。
$\qquad y_t=\rho y_{t-1}+u_t, \quad u_t \sim iid(0,\sigma^2)$
のOLS推定量は、
$\qquad \hat{\rho}= \rho+\frac{\sum_{t=1}^{T}y_{t-1}u_t}{\sum_{t=1}^{T}y_{t-1}^2}$
となり、検定統計量について、
$\qquad \tau_{\rho}=\sqrt{T}(\hat{\rho}-\rho)$
が$N(0,1-\rho^2)$に収束することが知られている。また、t検定の場合は
$\qquad \tau_t=\frac{\hat{\rho}-\rho}{\hat{\sigma}_{\hat{\rho}}}$
を用いて検定を行う。
ADF検定
- DF検定が真のモデルをAR(1)と仮定していたのに対し、真のモデルをAR(p)過程とするのがADF検定である。
- 真の過程を
$\qquad y_t=\phi_1 y_{t-1}+\cdots+\phi_p y_{t-p}+\epsilon_t, \quad \epsilon_t \sim iid(0,\sigma^2)$
と過程した上で、
$\qquad \left\{\begin{array}{ll}\rho=\phi_1+\cdots+\phi_p\\ \zeta_k=-(\phi_{k+1}+\cdots+\phi_{p}), \quad k=1,2,\cdots,p-1\end{array}\right.$
として、真の過程を
$\qquad y_t=\rho y_{t-1}+\zeta_1 \Delta y_{t-1}+\cdots+\zeta_{p-1}\Delta y_{t-p+1}+\epsilon_t$
と変形して推定することが多い。
PP検定
- Phillips-Perron(PP)検定は、ADF検定と比較した時に、$u_t$がiid系列ではなく、自己相関や分散不均一性を持つことを許容した検定である。
- PP検定では、
$\qquad u_t=\sum_{s=0}^{\infty}\psi_s\epsilon_{t-s}, \quad \epsilon_t \sim iid(0,\sigma^2)$
と定義した上で、
$\qquad \left\{\begin{array}{ll}\gamma_k=\sigma^2\sum_{s=0}^{\infty}\psi_s \psi_{t-s}, \quad k=0,1,2,\cdots\\ \lambda^2=\sigma^2(\sum_{k=0}^{\infty}\psi_k)^2\end{array}\right.$
を用いて統計量について、
$\qquad \tilde{\tau}_{\rho}=\tau_{\rho}-\frac{1}{2}\frac{T^2\hat{\sigma_{\hat{\rho}}}^2}{s^2}(\lambda^2-\gamma_0)$
$\qquad \tilde{\tau}_t=\bigl(\frac{\gamma_0}{\lambda^2}\bigr)^{\frac{1}{2}}\tau_t-\frac{1}{2\lambda}(\lambda^2-\gamma_0)\frac{T\hat{\sigma}_{\hat{\rho}}}{s}$
と修正したものを使用して検定を行う。
4. ADF検定の例
データ
- 前回に引き続きFI2010の板情報のデータを用いる。板の最良気配の値段と数量についてのデータであり、そこから仲値と数量の不均衡度合いを算出したものである。株価推移部分については以下のようなデータである。
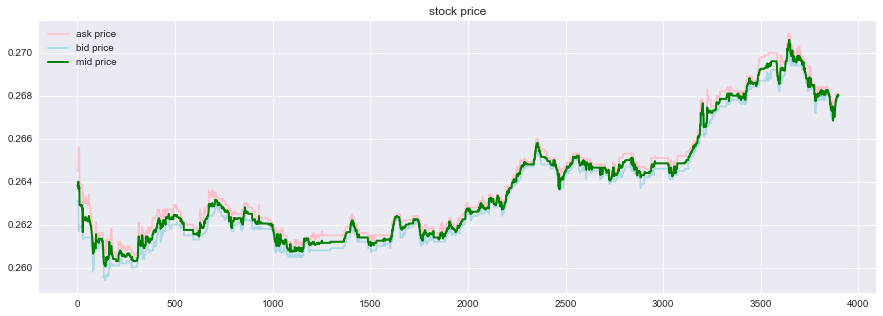
使用するライブラリについて
- ライブラリはstatsmodelsのadfuller を使用する。
statsmodels.tsa.stattools.adfuller(x,
maxlag=None,
regression='c',
autolag='AIC',
store=False,
regresults=False)
- 引数
- x
1Dのarray、ADF検定を行うデータ - maxlag
ADF検定を行う際のラグの最大値。真のモデルをAR(p)とした時のpが取りうる最大値をここで決める。デフォルトは
$\qquad 12\bigl(\frac{nobs}{100}\bigr)^\frac{1}{4}$
である。なお、$nobs$はADF検定に使われるサンプル数(データの長さ)である。 - regression
回帰モデルの定数とトレンドを指定する。- regression = 'c' 定数のみ
- regression = 'ct' 定数とトレンド
- regression = 'ctt' 定数と1次、2次のトレンド
- regression = 'nt' 定数もトレンドもなし
- autolag
ラグの最大値について。- autolag = None
maxlagで指定した値が用いられる。 - autolag = 'AIC' or 'BIC'
AICかBICの指定した方の情報量基準を用いてラグが決まる。 - autolag = 't-stat'
maxlagで指定した値から始め、t値が95%基準で有意となるまでラグの値を減らしていく。
- autolag = None
- store
Trueの際はADF検定の値に加え、結果のインスタンスを返す。 - regresults
Trueの際は回帰の結果のインスタンスを返す。 - 戻り値
- adf
ADF検定の統計量 - pvalue
検定のP値 - usedlag
モデルに採用されたラグの値 - nobs
回帰に使われたデータの個数 - critical values
検定の1,5,10%点の値 - icbest
autolagがNoneでない場合、情報量の最大値を返す。 - resstore
検定と回帰の結果のインスタンス
検定
- ここでは株価の仲値についてADF検定を行う。
sm.tsa.stattools.adfuller(pr['mid_p'], regression='c')
(-0.20323946357862777,
0.9381343788163952,
5,
3893,
{'1%': -3.4320308674757216,
'10%': -2.5671653561652974,
'5%': -2.862282715190103},
-62621.39909588861)
- このように結果が返ってくる。P値は0.938となっており0.05より大きいため、
単位根過程ではないという結論になりました。単位根過程であるという帰無仮説を棄却することはできませんでした。 - しかし、regressionのモデルを変えてやると結果が変化します。最もP値が小さくなったのは以下のケース。
sm.tsa.stattools.adfuller(pr['mid_p'], regression='ct')
(-3.157614947597485,
0.09318302029273301,
5,
3893,
{'1%': -3.9610973596684973,
'10%': -3.1277144258146876,
'5%': -3.411618364778587},
-62626.67403498432)
- トレンドを加えたモデルを使うとP値は0.05より小さくはなっていないものの、0.093になり、10%点よりは外側に来ています。株価がデータの期間では右肩上がりとなっており、トレンドを含めてやることが奏功した可能性があります。